基于随机森林的600 MW直接空冷机组背压运行优化
安留明,聂椿明,陈 衡,徐 钢,李 季
(华北电力大学热电生产过程污染物监测与控制北京市重点实验室,北京 102206)
近年来,我国电力行业发展迅猛,火电机组装机容量屡创新高。随着火电机组朝着更高参数、更大容量方向发展,火电厂每年消耗的水资源在逐年攀升。在我国富煤缺水的北方地区,贫乏的水资源成为限制电厂发展的一个重要问题。直接空冷技术对冷却水的需求相对较少,其利用空冷风机产生的冷风以强制对流换热的形式来冷却凝汽器中的乏汽,有效节约了水资源,在我国北方缺水地区得到广泛使用。然而,由于空气的导热系数仅为水的导热系数的1/25,所以空冷机组的背压和煤耗相对湿冷机组整体偏高。提高风机转速可以增强空气对流换热能力,有利于降低机组背压,增加机组发电出力,但是同时会引起风机耗功功率的增加。因此,寻找使得机组发电功率增量ΔNt与风机功率增量ΔNf之差(ΔNt–ΔNf)取得最大值的最佳背压成为提高机组经济性的有效措施。
目前,在直接空冷机组最佳背压的机理研究方面取得了很多进展。任岐[1]介绍了直接空冷系统的结构和组成设备,并对背压的主要影响因素做了分析。高建强等[2]基于机理分析建立了最佳背压优化模型,分析了背压变化对发电机功率和风机耗功的影响。郝润田[3]通过分析背压的影响因素,提出了不同运行工况下的背压控制方法。曹旭等[4]通过研究空冷风机的运行特性,计算得到了不同工况下的最佳背压值。郭民臣等[5]分析了机组变工况运行时环境温度、排汽热负荷和环境风速对背压的影响。
近年来,随着大数据、人工智能技术日趋成熟,机器学习与智能算法在电厂设备状态监测与运行优化方面得到了广泛的应用。李晓恩[6]采用数据驱动的方法对电站设备进行机理建模分析。卞韶帅等[7]基于机组运行数据建立了各类数据挖掘分析模型,对冷端系统进行诊断。潘云[8]通过BP神经网络和遗传算法对锅炉燃烧进行优化分析。采用机器学习算法建模的方法,可以充分挖掘机组运行数据的价值。以机组运行数据为切入点,通过建立各个输入与输出的映射关系模型,结合数据可视化技术可以更直观地分析各个输入对研究对象的影响程度,进而确定机组各个工况下的最优状态,并给出相应的输入值。因此,本文基于某电厂600 MW直接空冷机组运行数据,采用随机森林算法建立了不同工况下的机组净功率-背压模型,进而得到了相应的最佳背压值,为指导空冷机组的背压运行优化提供了借鉴和参考。
1 随机森林算法介绍
集成学习包括多个单一的学习机。研究表明,集成学习机相对单一学习机有更高的泛化能力和预测准确率[9]。集成学习可以用来解决分类和回归问题,是机器学习框架的一种。随机森林算法属于集成学习的一种类型,具有灵活度高、不易过拟合、准确率高的特性,有广阔的应用场景[10]。
随机森林包含多颗决策树。决策树是由节点和树枝组成的二叉树结构。决策树自上向下依次进行分裂,初始样本经过根节点分裂为2个新的子节点,随机选取某些属性后继续分裂到下一层的叶子节点,如此不断分裂直到最后的叶节点。叶节点是代表对应的类或预测输出的一类样本,不可再继续分裂[11-12]。图1为随机森林预测模型的构建流程。

图1 随机森林预测模型构建流程Fig.1 Flow chart of stochastic forest prediction model construction
其具体构建步骤为[13-14]:1)随机抽样训练决策树,利用Bootstrap重采样法从初始样本集S有放回地抽取了n个样本,这n个样本生成m(m 本文的样本数据来自某超临界2×600 MW直接空冷机组。空冷岛由56台风机单元组成,其额定功率为132 kW,按照8排7列布置。其中包括顺流区40台风机、逆流区16台风机,风机直径为9.754 m,额定转速为73 r/min,额定风量为573 m3/s,功率因数为0.87;空冷机组的换热管束由单排翅片管组成,翅片管材料为碳钢/铝翅片,翅化比为123,总散热面积为1 423 460 m2。 利用机组的厂级监控信息系统(SIS)直接提取了机组2018年1月至2019年3月运行期间的负荷、背压、环境温度、环境风速、主蒸汽压力、主蒸汽流量、主蒸汽温度、给水流量、凝结水流量、凝结水温度、风机转速、风机轴温、风机电流、风机母线电压14个测点的数据。本文对56台风机的轴温测点数据取均值作为最终的风机轴温测点数据。由于风机转速也有56个测点数据,对56个风机转速进行累加求和得到风机的总转速。在取出每台空冷风机的电流值后,风机群耗功功率可以采用式(1)计算得到 式中:P为56台风机耗功总功率,kW;Uj为第j排风机母线电压,V;Ujk为第j排第k列风机电流,A;cosφ为风机相位角余弦值,取0.87。 在算出风机群耗功之后,计算同一时刻下的机组负荷与风机群耗功的差值作为机组净功率。本文选取2018年全年数据作为建模数据,2019年3月份数据作为测试验证数据。 实测数据中往往存在缺失值、离群值和噪声,此时就需要进行数据预处理,以确保准确、高效和有意义的分析[15]。本文使用MATLAB软件通过数据筛选的方法来剔除原始数据中存在的停机工况、缺失值的数据。同时根据机组和空冷岛的设计和热力试验资料设置了部分运行参数的范围,详见表1。参数外的运行数据视为非正常运行工况,对其进行剔除处理以利于提高模型的准确性。 表1 机组运行数据参数范围Tab.1 Range of unit operation data parameters 灰色关联分析法可以用来判断1组数据中相关因子对所选研究因子的影响强弱程度,这种影响程度可以用关联系数来衡量。关联系数具体计算步骤如下[16-18]: 步骤1 选定要研究的因子数据作为母序列,对研究因子有影响的相关因子数据作为子序列。 步骤2 为消除量纲差异造成的影响,需要对母序列、子序列进行无量纲归一化处理,处理后的数值在0~1之间。 步骤3 计算母数列与子数列的关联系数。对于一个母序列x0有若干个子序列x1,x2, …,xn,各母序列与子序列间的关联系数可由式(2)算出。其中:ρ为调节系数,取值为0~1之间,一般取0.5;xi(k)表示第i个子序列的第k个数值。 步骤4 计算关联系数。对不同时刻子序列与母序列间的关联系数取均值,作为整体上的关联系数。关联度公式为 式中ri值越接近1,说明相关性越好。 在已有测点中选取机组净功率作为母序列,其他11个测点与机组净功率有关的测点(背压、风机总转速、环境温度、主蒸汽压力、主蒸汽温度、风机轴温、凝结水流量、主蒸汽流量、凝结水温、给水流量、环境风速)作为子序列,求得机组净功率与各测点的关联系数如图2所示。 由图2可见,主蒸汽流量、凝结水流量、主蒸汽压力、主蒸汽温度、给水流量因与机组负荷密切相关,进而影响机组净功率,其关联系数较高。为了减少数据冗余和提高背压变化对机组净功率的响应灵敏度,保留主蒸汽流量作为建模变量。凝结水温度因与背压密切相关,其随背压变化影响机组净功率,二者保留背压作为建模变量。风机总转速、风机轴温因与风机群耗功相关,进而影响机组净功率。因为空冷机组主要依靠调节风机转速来改变机组背压,后文需要采用控制变量法分析仅改变背压对机组净功率的影响,故风机转速不能作为建模变量,可保留风机轴温作为建模变量。环境风速、环境温度作为主要影响空冷机组冷端运行状况的因素,也保留作为建模变量。 图2 各变量与机组净功率间的关联系数(2018年数据)Fig.2 Correlation coefficient between data variables and unit net power in 2018 最佳背压是指使得机组发电功率增量ΔNt与风机功率增量ΔNf之差ΔNt-ΔNf取最大值时所对应的背压值。一般需要建立机组发电功率-背压模型和风机功率-背压模型,然后选定起始工况点,分别计算机组发电功率增量-背压、风机功率增量-背压的数值关系,最后做出机组净功率增量-背压函数曲线以求得最佳背压[19-21]。由于需要建立2个模型,导致累加误差较大,同时根据取出的机组负荷、风机群耗功数据作差计算得到了机组净功率,所以考虑直接建立机组净功率-背压模型来寻找最佳背压。 由于机组运行数据集中在300 MW以上,本文以300 MW为起始点,30 MW为步长,分别计算了11个典型负荷下不同环境温度下的最佳背压。最佳背压计算流程如图3所示[22]。具体计算步骤如下: 图3 最佳背压计算流程Fig.3 Flow chart of the optimal back pressure calculation 1)选取典型负荷数据,即300、330、360、390、420、450、480、510、540、570、600 MW。每个负荷附近±2 MW都作为该负荷的数据。 2)在每一负荷下,从0~35 ℃每隔5 ℃选取1个温度值,这样一共划分了88个工况。每个环境温度附近±0.5 ℃都作为该温度的数据。如9.5~10.5 ℃内的数据归为10 ℃的数据。 3)采用随机森林分别建立每个工况下的机组净功率-背压关系模型。随机选取每个工况下4/5的数据作为训练集,1/5的数据作为测试集数据。 4)通过调节建模参数改善建模精度,直到测试集的平均相对误差在0.5%以下。 5)对负荷、环境温度划分后的数据集取平均值作为该工况下的典型值。以平均背压为中心,其增减3 kPa为上下界,采取穷举法,步长设为0.1 kPa,生成背压寻优区间,其他边界条件取典型值保持不变,代入模型寻找机组净功率最大值对应的背压,即为最佳背压。 以环境温度20 ℃、机组负荷420 MW范围内数据为例,采用随机森林算法建立机组净功率-背压关系模型,模型输入变量选取为背压、主蒸汽流量、风机轴温、环境温度、环境风速,输出变量为机组净功率。 采用循环试验法确定随机森林算法中回归树颗数“Ntrees”和最小叶子节点“MinleafSize”2个主要的建模参数以满足模型误差要求。在随机森林的Bootstrap重采样过程中,每次约有1/3的数据未被选中参加回归树的训练过程,这些数据称为袋外数据(out of bagdata),可以取代测试集作为一种误差估计方法。 李蔚等[23]给出“Ntrees”范围一般为50~200,默认取为50。为了确定最佳回归树颗数“Ntrees”的取值,取回归树颗数分别为50、100、150、200时建模观察袋外观测数据的均方误差,如图4所示。从图4可知,随着回归树颗数的增加,均方误差快速下降,最后趋于平缓。回归树颗数为200时模型的均方误差最小。 图4 不同回归树颗数的袋外均方误差Fig.4 The out-of-bag mean square error for different numbers of regression tree 对于回归,一般的规则是将最小叶子节点数“MinleafSize”设置为5,可以通过比较不同叶子节点数对应的回归均方误差来确定最佳叶子节点。不同最小叶子结点下的均方误差如图5所示。由图5可知,叶子节点为5时的均方误差最小。 图5 不同最小叶子结点下的均方误差Fig.5 The mean square errors with different min leaf sizes 为了比较随机森林参数调节后该工况下的测试集误差能否满足模型误差要求。引入平均绝对误差δMAE、平均相对误差δMAPE、均方误差δMSE、决定系数R2等4个评价指标。测试结果见表2。 表2 随机森林回归模型调参前后的误差对比Tab.2 The errors of random forest regression model before and after the parameter adjustment 由表2可知,模型调参后的δMAE、δMAPE、δMSE等均小于调参前的数值,模型精度有所提升。调节前后均能满足模型平均相对误差小于0.5%的要求。决定系数R2的取值范围是[0,1],R2越接近1则模型拟合效果越好。 经过计算,环境温度为20 ℃,负荷为420 MW时的机组净功率-背压关系如图6所示。从图6可知,随着背压增大,机组净功率先增大后减小,在背压为8.6 kPa时机组净功率达到最大。所以,环境温度为20 ℃时,该负荷下的最佳背压值为8.6 kPa。 图6 机组净功率-背压关系Fig.6 The relationship between net output and back pressure of the unit 同样地,使用随机森林算法建立各负荷下不同环境温度下的机组净功率-背压关系模型可以得到相应的最佳背压值。为便于进一步观察,绘制不同负荷下的最佳背压与环境温度的关系,如图7所示。 图7 各负荷段内最佳背压与环境温度的关系Fig.7 Change trends of the optimal back pressure with ambient temperature at different loads 从图7可以看出,最佳背压随着环境温度、负荷的增大而增大,且环境温度越高最佳背压随负荷的增大速率越大。环境温度较低时,最佳背压随负荷增大变化范围较小;环境温度较高时,最佳背压随负荷增大显著增大。 通过计算最佳背压下的机组净功率与运行数据中实际背压下的净发电功率差值,并把计算得到的差值以时间为横坐标进行积分计算,可以得到累计节电量。在对不同负荷下的节电量进行比较时,为了消除不同负荷下的数据量不同造成的计算结果差异,把每个负荷下的节电量除以该负荷下的数据量得到了单个样本的平均节电量。由于建模数据取自直接空冷机组的厂级监控信息系统(SIS),样本数据间隔为30 s,为了便于计算,将每个样本点数据在30 s内近似看作不变,所以累计节电量和单个样本的平均节电量计算公式见式(4)、式(5)。 通过计算2019年3月份背压优化后的节电量,可以对2018年数据得到的最佳背压表进行节能效果评估。首先,将3月份运行数据中的实际背压替换为最佳背压;然后,同样按负荷、环境温度进行数据分群;最后,把替换为最佳背压后的分群数据代入2018年对应的分群工况模型中求出最佳背压下的机组净功率。 背压替换过程为:根据表3对2019年3月份数据进行线性插值可以得到相应的最佳背压值。 本文采用了MATLAB中三维插值函数griddata来实现插值过程,griddata函数支持在指定的查询点对曲面进行插值并返回插值结果,插值方法包括“linear” “nearest”“natural”“cubic”“v4”5种,这里选用了“linear”进行线性插值。具体步骤为:1)以表2中的环境温度、负荷、最佳背压值分别为x、y、z轴生成网格化的插值曲面;2)以2019年3月份运行数据中的负荷、环境温度为插值查询点,对其进行插值。插值结果如图8所示。 图8 2019年3月份插值背压Fig.8 The interpolation back-pressure diagram in March,2019 为进一步观察最佳背压优化前后不同负荷段下的机组净功率的变化以评估最佳背压的节能效果,选取2019年3月份环境温度20 ℃,负荷为330、420、510 MW的各100个样本数据点,分别绘制了优化前后的背压和机组净功率对比图(图9、图10)。由图9、图10可以看出:机组实际背压和优化背压随着负荷的增大而增大,330 MW时,机组优化运行背压大都在8 kPa以下,510 MW时机组的优化背压多数达到9~10 kPa;不同负荷下的优化背压大部分小于实际背压,且背压优化后的机组净功率较优化前有所提升,这说明适当降低机组背压有利于增大机组净功率。由图10可知,不同负荷下背压优化后的机组净功率大于优化前的机组净功率,这说明了2018年数据得到的最佳背压表在指导背压优化方面有一定的参考价值。 图9 不同负荷下背压优化前后对比Fig.9 Comparison of back pressure before and after optimization at different loads 图10 不同负荷下背压优化前后机组净功率对比Fig.10 Comparison of unit net output before and after back pressure optimization at different loads 为进一步评估不同负荷下背压优化后的机组节能效果,采用式(4)、式(5)计算了300~600 MW范围内各典型负荷下的累计节电量和单个样本的平均节电量,结果见表3。 表3 背压优化后不同负荷下的节电量 单位:kW·hTab.3 The energy saving at different loads after back pressure optimization 由表3可知:在300~450 MW低负荷范围内,机组单个样本的平均节电量在5 kW·h以上;当机组负荷升高到480 MW时,其单个样本的平均节电量小于5 kW·h。由此可见,低负荷阶段机组使用最佳背压优化后的节能效果更好,其相应的机组净功率增量更显著。 本文基于机组运行数据建立了不同环境温度、负荷数据群下的机组净功率-背压模型,通过模型得到了机组不同工况下的最佳背压表。根据2018年运行数据得到的最佳背压表,采用线性插值的方法对2019年3月份的实际背压进行了替换优化,计算优化后的机组净功率,得到了如下结论: 1)最佳背压随着环境温度、负荷增大而增大,且环境温度越高最佳背压随负荷的增大速率越大。 2)环境温度为20 ℃时,优化背压大都小于实际背压,适当降低运行背压有利于增大机组净功率。 3)不同负荷工况下的机组净功率优化效果不同,机组在低负荷下的净发电功率增量更显著。 4)背压优化后2019年3月份的机组净功率有所提高,这表明2018年数据得到的最佳背压表在指导背压优化方面有较大参考价值。2 数据处理和模型建立
2.1 空冷岛介绍及数据来源

2.2 数据预处理

2.3 模型变量选取



2.4 模型建立
2.5 建模参数的确定与误差分析



3 计算结果及评估
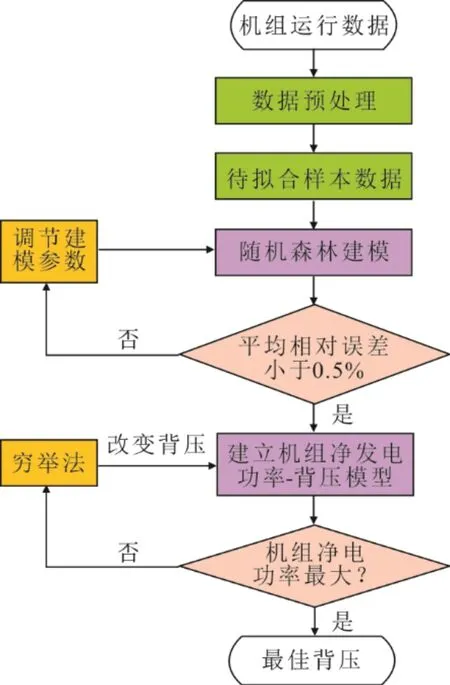
3.1 最佳背压计算


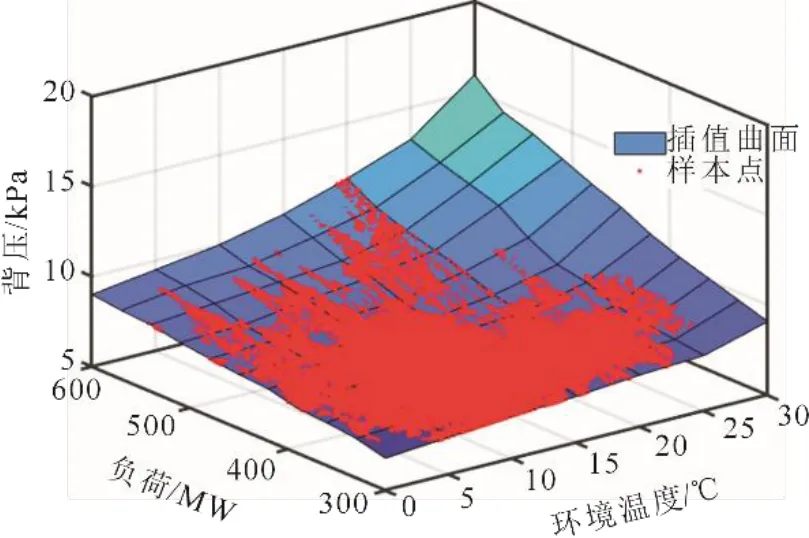
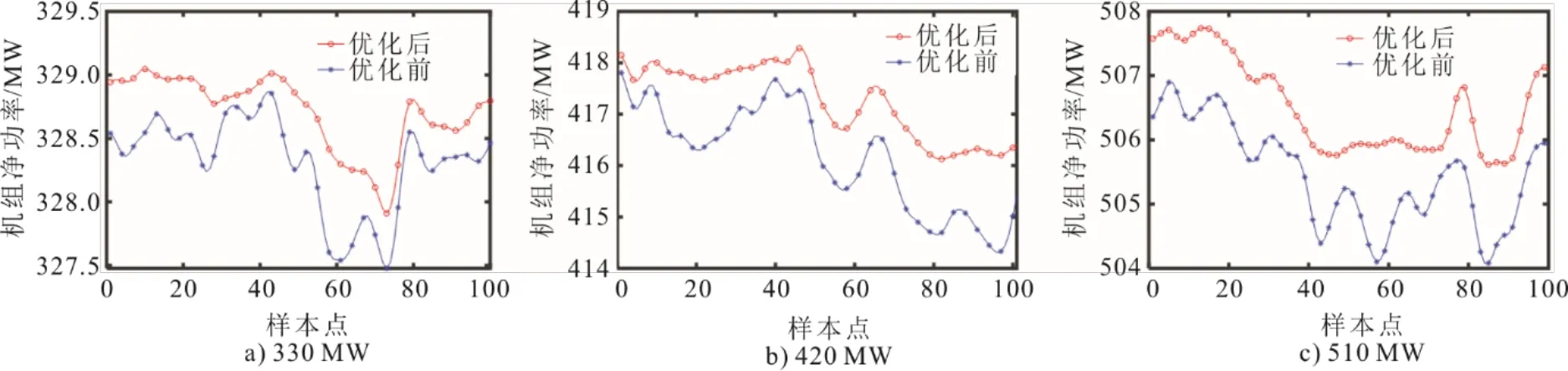
3.2 节能效果评估



4 结 论

