均压槽气体静压轴承承载性能研究*

王 婷，张 浩，杨佳成，陆晨飞

(南京工业大学机械与动力工程学院，南京 211800)

0 引言

随着超精密加工技术的不断发展，人们对零件的精度要求越来越高，以传统的滚动轴承和液体润滑轴承作为支撑的加工和测量仪器已经难以满足需求[1]。气体静压轴承虽然具有运动精度高、摩擦小、低速进给无爬行、无污染、发热低等优点，但由于气体的可压缩性，导致提高轴承的承载力和刚度比较困难[2]。由于气体静压轴承的承载力小、刚度低、稳定性差、制造精度要求高，导致气体静压轴承的应用范围受到很大限制。因此，很多学者在计算方法、轴承结构、节流器结构等方面对气体静压轴承进行了广泛地研究，以提高轴承的承载力、刚度和稳定性[3-5]。

Lai T等[1]分析了节流孔孔径、个数、排布方式以及供气压力等因素对气体静压导轨承载力和刚度的影响，并进行了实验验证。Aoyama T等[6]设计了一种出口形状为圆角的节流孔，通过仿真计算与实验验证，证明与出口为直角的节流孔相比，圆角的节流孔可以有效抑制轴承的振动。Xiao H等[7]详尽地分析了轴承的直径、转速、偏心率以及节流孔直径和供气压力等参数对气体静压径向微轴承的承载力和刚度的影响，并通过实验进行验证。Zhang J B等[8]采用求解层流边界层方程的分离变量法详细地分析了气膜厚度、节流孔孔径、供气压力对轴承的径向压力分布以及承载力和刚度的影响。Du J等[9]系统地研究了均压槽的个数、开设形式、尺寸参数等因素对气体轴颈轴承承载力和刚度的影响，并进行了实验验证。Chen M F等[10]分析了X形均压槽气体静压轴承的静态和动态性能，并将计算得到的承载力与实验结果进行比较。于普良等[11]设计了一种辐射状径向槽气体静压轴承，分析不同的均压槽结构以及供气压力对轴承静态承载性能的影响。Gao S Y等[12]研究了人字槽对高速主轴的气体静压径向轴承的影响，并通过实验进行了验证。

本文以超精密微小型数控机床的气浮导轨为研究对象，在气体静压轴承顶部的工作面上开设了直线形、双弧形以及X形三种结构的均压槽，综合考虑轴承顶部和底部气膜对轴承的作用，通过计算得到了轴承的承载力W、刚度K和气体质量流量M，确定使轴承具有最佳承载性能的均压槽结构，并进一步对该均压槽的宽度、深度和节流孔的个数对轴承承载性能的影响规律进行了分析，得到了优化的均压槽尺寸。

1 气体静压轴承模型及参数设置

1.1 物理模型

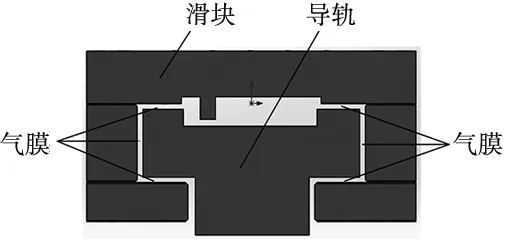
图1 气体静压轴承简化物理模型

气体静压轴承简化后的物理模型如图1所示。该轴承主要由导轨和滑块两部分组成，外部气源设备产生的高压气体被引入轴承后，流经轴承内部的供气管路，经过节流孔进入导轨与滑块之间的间隙，形成具有一定承载能力和刚度的气膜，实现润滑轴承与承载负载的作用，之后气体从轴承端部流出。

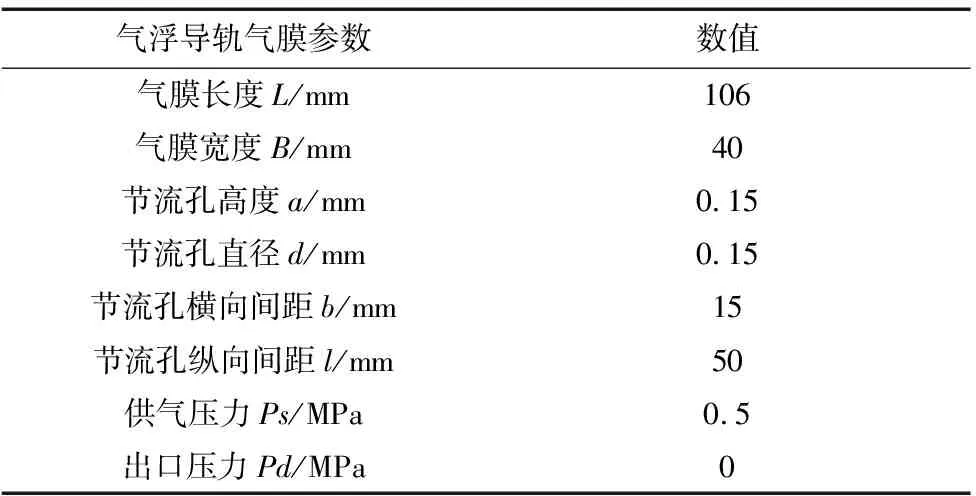
轴承的受力情况如图2所示。轴承受到滑块自身的重力G以及外部的负载力W和6个气膜产生的气膜力F，气膜力中对轴承的承载能力起作用的力为F11，F12，F31，F32，其中F31和F32与重力方向相同，F11和F12与重力方向相反。为保证轴承的承载力，需满足W=F11+F12-F31-F32-G>0。在轴承顶部的双排节流孔出口处加工横截面形状为矩形的均压槽可以增大F11和F12，从而提高轴承的承载力。由于轴承顶部、两侧和底部各自的两部分气膜结构尺寸完全相同，因此以气膜上分布有12个节流孔的轴承为例，轴承气膜的结构如图3所示，双排节流孔等距分布在气膜内部，气膜的尺寸参数如表1所示。

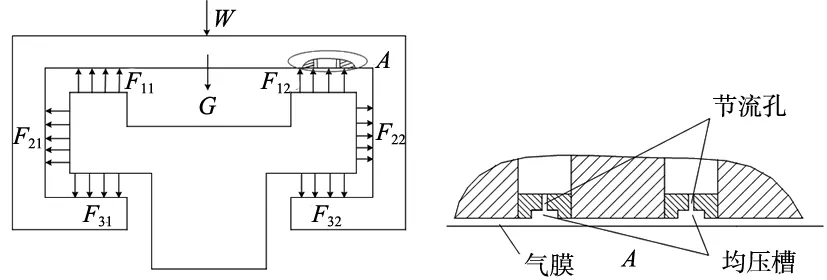
图2 轴承受力示意图

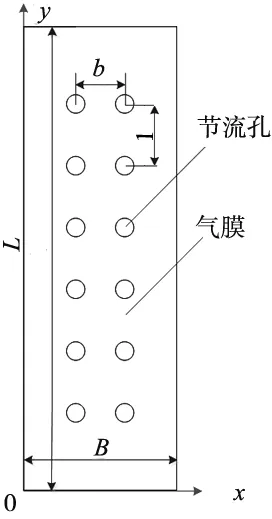
图3 轴承气膜结构示意图

表1 气膜的尺寸参数

1.2 控制方程

轴承的承载能力通过计算轴承气膜的压力分布得到，在计算前需要做出以下假设[13-14]：

(1)气膜内部气体的流动符合牛顿运动定律；

(2)气膜内部气体在流动过程中是等温的；

(3)气膜内部气体的流动模式为层流；

(4)气膜内部气体为连续的单相介质。

连续性方程[15]：

(1)

其中，ρ为气膜内气体的密度；t为均压槽横截面的高度；u为气体在x方向的速度；v为气体在y方向的速度；w为气体在z方向的速度。

等温气体的状态方程[13]：

(2)

其中，p为轴承工作面的气膜压力；g为重力加速度；R为气体常数；T为气体的绝对温度。

气体流动状态为层流的简化雷诺方程[16]：

(3)

其中，h为气膜厚度；μ为气体的粘度。

气膜承载力的计算公式：

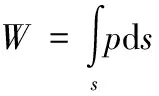
(4)

其中，s为气体静压轴承有效工作面面积，即轴承顶部和底部的气膜面积。

轴承受到外载荷作用时，其顶部和底部的气膜厚度会产生相同的尺寸变化，顶部气膜受压变薄，底部气膜变厚。假定气膜的变化量为Δh，则根据偏心率e，可以得到轴承在不同偏心率下的刚度。

其中，偏心率e的计算公式为：

(5)

刚度的计算公式为:

(6)

其中，ΔW为承载力的变化量。

2 数值仿真方法可靠性验证

为验证数值仿真计算的可靠性，利用文献[17]中已有的气浮轴承静态模型及压力分布数据，建立模型并进行CFD层流计算。文献[17]中的气浮轴承模型如图4所示，节流孔半径R1=0.25 mm，轴承半径R2=5 mm，气膜厚度h0=6.3 μm，节流孔高度a1=1 mm，入口压力Ps=0.49 MPa，出口压力Pd=0 MPa，气体设置为理想气体，气体温度为293 K，层流模型仿真结果和实验结果如图5所示。从图中可以看出，层流仿真计算的结果与文献[17]中的实验结果高度一致，证明了层流仿真对气浮轴承性能计算的可靠性和真实性。

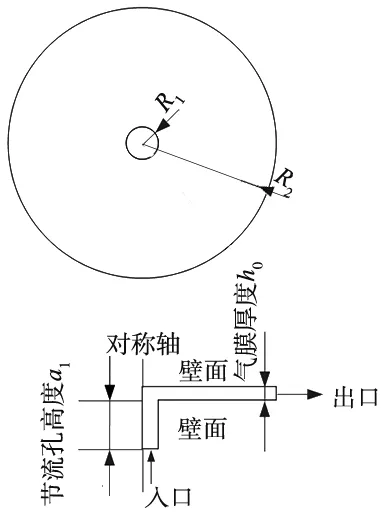
图4 气体静压轴承结构示意图

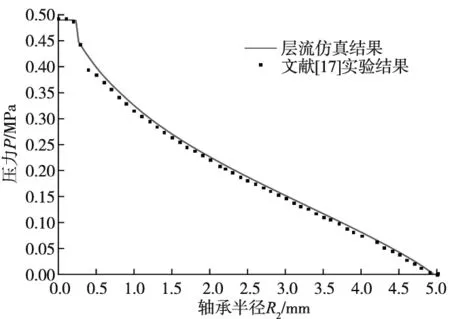
图5 层流模型仿真结果和实验结果对比

3 气体静压轴承仿真分析

3.1 边界条件设置

本文设计了直线形、双弧形以及X形三种横截面为矩形的均压槽，三种均压槽轴承以及无均压槽轴承的气膜模型如图6所示。随着CFD的蓬勃发展，使得气体静压轴承仿真计算过程中可能会遇到的计算量大、计算困难的问题得以解决。本文利用有限元仿真软件Workbench的FLUENT模块对气体静压轴承的气膜部分进行流体仿真计算。从图6中看出气膜上下对称，为提升计算速度，取气膜的一半进行仿真计算。气膜的入口设置为压力入口，入口压力Ps=0.5 MPa，三个出口设置为压力出口，出口压力Pd=101.325 MPa，设置气膜剖面为对称面，其余面为壁面，计算采用层流模型，其余参数使用默认参数。

以轴承气膜厚度为20 μm为例，经过仿真计算得到轴承气膜的压力云图如图7所示，气膜沿竖直轴线方向的压力分布曲线如图8所示。由图7可以看出，与没有均压槽的轴承气膜相比，有均压槽的轴承气膜压力明显得到提高，高压区范围显著增大，压力分布也更加平稳。从图8中可以看出，与无均压槽的轴承气膜相比，有均压槽的轴承气膜压力整体得到大幅度提升，从气膜边缘到第一个节流孔之间，压力的提升速度更快，在分布有均压槽的位置，气膜压力基本平稳保持在0.5 MPa。在节流孔分布的范围内，无均压槽轴承的最小压力仅有0.16 MPa，而设计有均压槽轴承的最小压力约为0.48 MPa，说明设计均压槽结构可以有效提高轴承的承载能力。

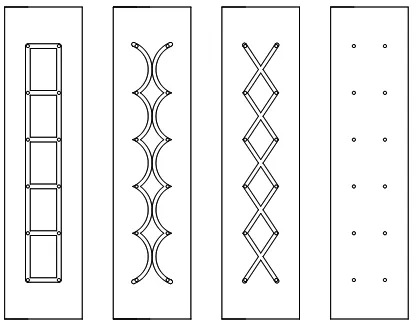
图6 均压槽轴承气膜模型

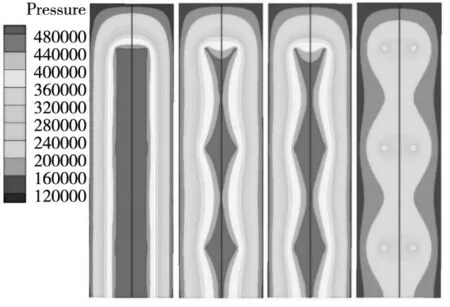
图7 轴承气膜压力云图

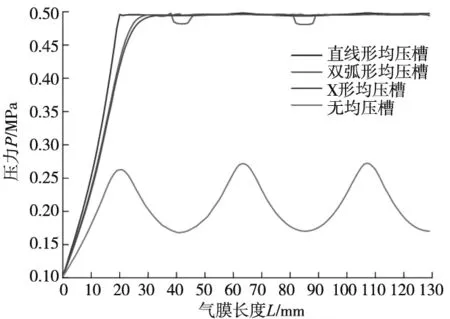
图8 轴承沿气膜轴线方向的压力分布曲线

3.2 均压槽结构对轴承承载性能的影响

在均压槽高度t=0.2 mm，均压槽宽度e=0.4 mm，节流孔直径d=0.2 mm,节流孔高度a=0.5 mm，节流孔个数m=12，入口压力Ps=0.5 MPa，出口压力Pd=0.1 MPa的条件下，分析了直线形、双弧形及X形均压槽在不同的偏心率下对轴承承载性能的影响，计算结果如图9所示。

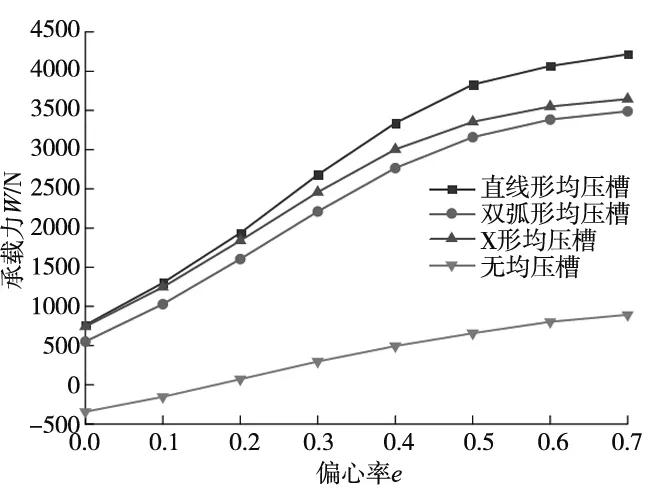
(a) 不同均压槽结构的轴承承载力

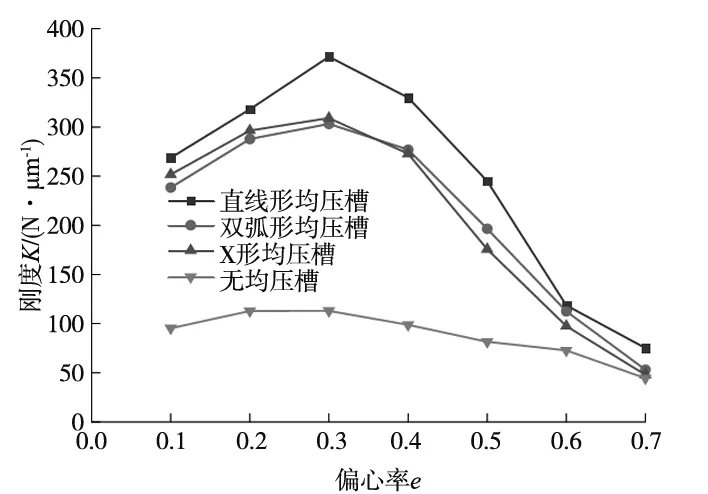
(b) 不同均压槽结构的轴承刚度

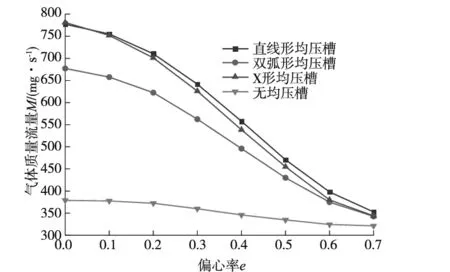
(c) 不同均压槽结构的轴承气体质量流量图9 均压槽结构对轴承承载力、刚度和气体质量流量的影响

从图9a中可以看出，随着偏心率的增大，轴承的承载力逐渐增大；同一偏心率下，直线形均压槽对应的轴承承载力最大，X形均压槽次之，双弧形均压槽对应的承载力最小。偏心率越大，直线形均压槽对承载力的提升效果越明显。无均压槽的轴承在偏心率e<0.2时，承载力为负值，最大承载力也仅有890 N，通过设计均压槽，轴承的承载力最大达到了4200 N，约提高为原来的4.7倍。

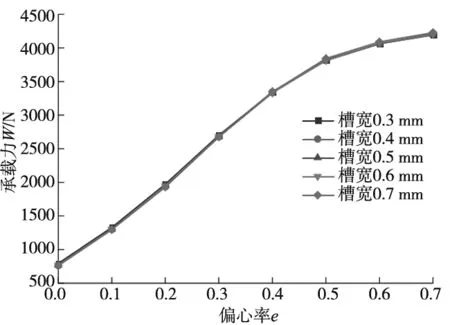
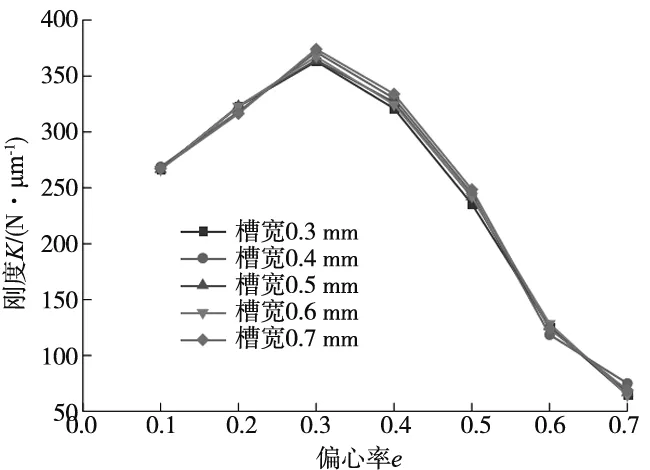
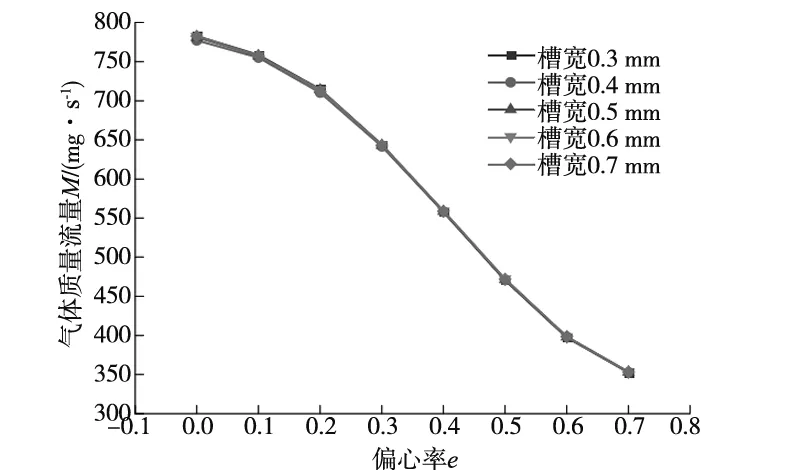
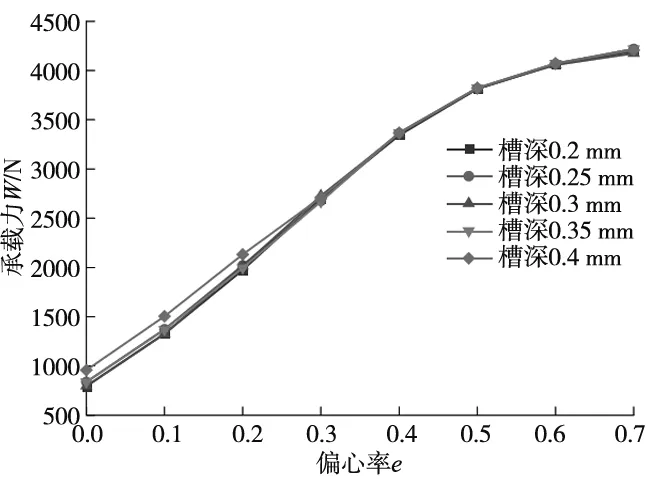
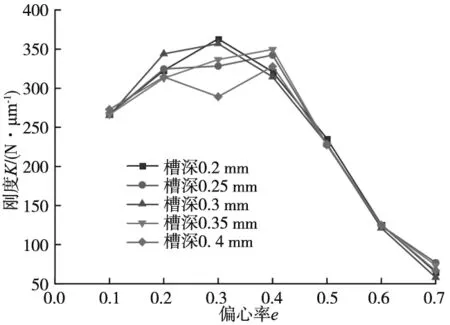
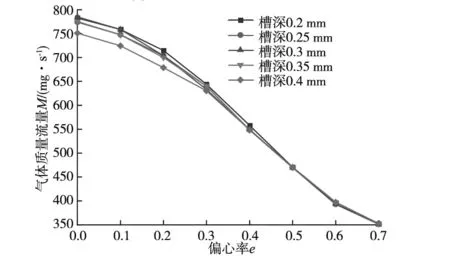
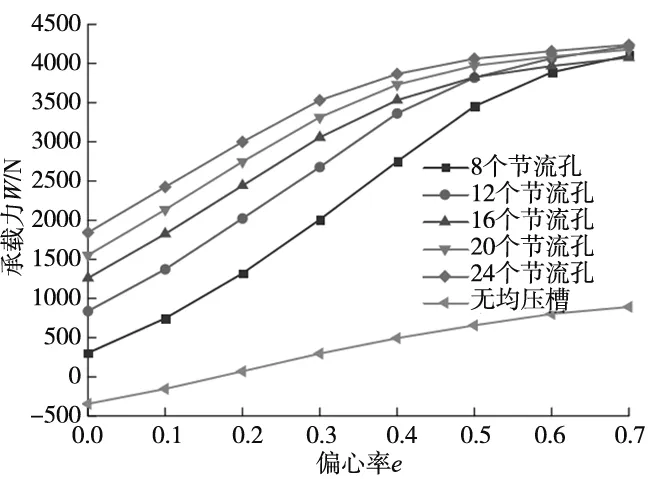
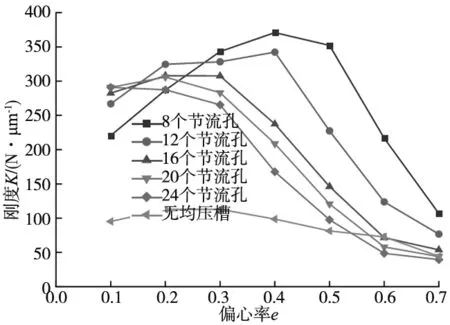
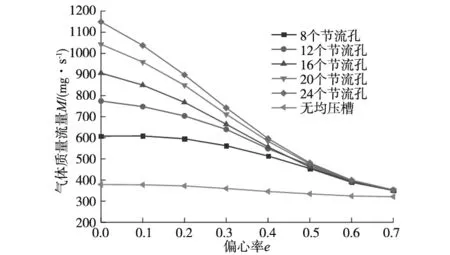
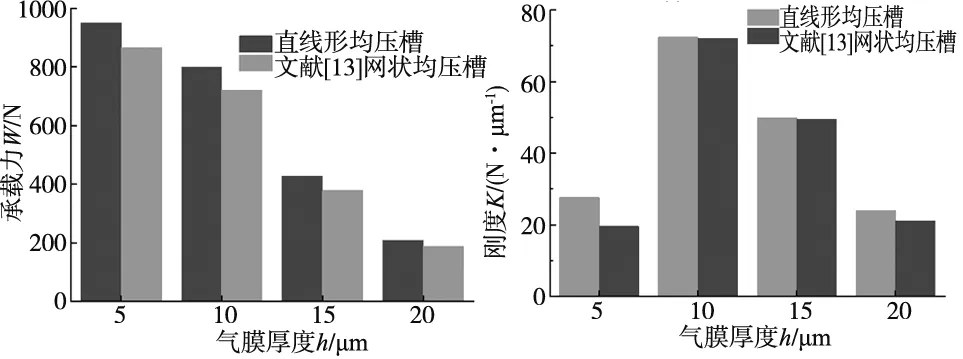
从图9b可以看出，随着偏心率的增大，轴承刚度先增大后减小；同一偏心率下，直线形均压槽对应的轴承刚度最大，而双弧形与X形均压槽对应的刚度相近；直线形均压槽在偏心率0.2

从图9c可以看出，随着偏心率的增大，轴承的气体质量流量逐渐减小；同一偏心率下，直线形和X形均压槽轴承的气体质量流量较大，双弧形均压槽轴承的气体质量流量则较小；与无均压槽轴承对应的气体质量流量相比，设计均压槽不可避免地增加了轴承的耗气量，最大约为无均压槽时的2倍。

3.3 均压槽宽度对轴承承载性能的影响

通过上节分析可知，直线形均压槽对轴承承载力和刚度的提升效果最好。因此，本节分析在其他条件不变的情况下，直线形均压槽宽度e分别为0.3 mm、0.4 mm、0.5 mm、0.6 mm、0.7 mm时，轴承承载性能的变化规律，仿真计算的结果如图10所示。

(a) 不同槽宽的轴承承载力

(b) 不同槽宽的轴承刚度

(c) 不同槽宽的轴承气体质量流量图10 均压槽宽度对轴承承载力、刚度和气体质量流量的影响

由图10a可以看出，轴承承载力随着偏心率的增大而增大；同一偏心率下，增大槽宽对轴承的承载力没有明显的影响，但当偏心率e<0.4时，槽宽为0.3 mm的轴承具有最大的承载力，当e>0.4时，轴承的承载力随着槽宽的增大有一定程度的增加。

由图10b可以看出，轴承的刚度随着偏心率的增大而先增大后减小；同一偏心率下，具有不同槽宽的轴承刚度都在偏心率为0.3时达到峰值，槽宽对轴承的刚度几乎没有影响。

由图10c可以看出，轴承的气体质量流量随着偏心率的增大逐渐减小，但是不同的均压槽宽度对轴承的气体质量流量没有明显影响。

3.4 均压槽深度对轴承承载性能的影响

通过上节分析可知，均压槽宽度对轴承的承载性能并无显著影响。由于均压槽使气膜中包含的气体体积增大，容易引起轴承的气锤自激振动，所以均压槽尺寸应该在满足使用要求的前提下尽量小一些[18]。因此，本节分析在直线形均压槽宽度e=0.3 mm，其他条件不变的情况下，均压槽深度t分别为0.2 mm、0.25 mm、0.3 mm、0.35 mm、0.4 mm时，轴承承载性能的变化规律，仿真计算的结果如图11所示。

(a) 不同槽深的轴承承载力

(b) 不同槽深的轴承刚度

(c) 不同槽深的轴承气体质量流量图11 均压槽深度对轴承承载力、刚度和气体质量流量的影响

由图11a可以看出，轴承的承载力随着偏心率的增大而不断增大；同一偏心率下，当e<0.3时，槽深越大，其对应轴承的承载力也就越大，当e≥0.3时，不同的槽深对承载力无明显影响。

由图11b可以看出，除槽深为0.4 mm的轴承刚度在e=0.3时出现小幅度波动外，其余槽深的轴承随着偏心率的增大，其刚度先增大后减小；同一偏心率下，当e<0.5时，适当增大槽深可以提高轴承的刚度，但当槽深过大时，会导致轴承的刚度减小。

由图11c可以看出，轴承的气体质量流量随着偏心率的增大不断减小；同一偏心率下，当e<0.5时，随着槽深的增大，轴承的气体质量流量逐渐减小，当偏心率e处于其余值时，槽深对轴承的气体质量流量无明显影响。

3.5 节流孔个数对轴承承载性能的影响

由图6可知，直线形均压槽以节流孔为结点互相连通，因此，节流孔的个数决定了均压槽的个数。本节分析在均压槽的宽度e=0.3 mm，深度t=0.25 mm，其他条件不变的情况下，节流孔个数m分别为8、12、16、20、24时，轴承承载性能的变化规律，仿真计算的结果如图12所示。

(a) 不同节流孔个数的轴承承载力

(b) 不同节流孔个数的轴承刚度

(c) 不同节流孔个数的轴承气体质量流量图12 节流孔个数对轴承承载力、刚度和气体质量流量的影响

由图12a可以看出，随着偏心率的增大，轴承的承载力不断增大，当偏心率达到0.6后，承载力的增加趋于平稳状态；同一偏心率下，轴承的承载力随着节流孔个数的增加而增大，并且随着偏心率的增大，不同节流孔个数对应的轴承承载力差距越来越小，当偏心率增达到0.7时，承载力基本没有差别。这说明当偏心率较小时，增加节流孔个数对承载力的提升效果最明显。

由图12b可以看出，随着偏心率的增大，除节流孔个数为24的轴承刚度一直降低之外，其余节流孔个数对应的轴承刚度先增大后减小；同一偏心率下，当偏心率e=0.1时，节流孔个数越多，对应的轴承刚度越小，当e>0.1时，节流孔个数越少，其对应轴承的刚度越大，并且不同的节流孔个数轴承的刚度峰值处于不同的偏心率，节流孔个数越多，其刚度峰值对应的偏心率就越小。

由图12c可以看出，随着偏心率的增大，轴承的气体质量流量逐渐减小；同一偏心率下，节流孔个数越少，其对应的轴承气体质量流量越小，当偏心率增大时，不同节流孔个数对应的轴承气体质量流量之间的差距越来越小。

以12个节流孔的轴承为例，设计直线形均压槽并对其尺寸进行优化后，轴承的承载力最大约提高4.8倍，刚度提高约3.5倍。

3.6 直线形均压槽性能验证

文献[13]研究了气浮导轨的4个节流孔分别为直线分布和矩形分布时，在气浮导轨的工作面上设计多种结构的均压槽对气浮导轨承载性能的影响。经过详细地分析确定，网状均压槽气浮导轨具有最优越的承载力和刚度。文献[13]中分析的气膜模型参数如表2所示，将本文中的直线形均压槽结构施加到该气浮导轨上进行仿真计算，得到的数据与文献[13]中的数据进行比较，对比结果如图13所示。由图13可以看出，与文献[13]中的网状均压槽相比，本文设计的直线形均压槽可以使文献[13]中的气浮导轨获得更优的承载力和刚度，证明结构更加简单的直线形均压槽更好地实现对轴承承载能力的提升。

表2 模型参数和分析条件设置

(a) 承载力对比 (b) 刚度对比图13 直线形均压槽轴承与文献[13]中的网状均压槽轴承承载力与刚度对比

4 结论

本文在气体静压轴承的工作面上设计了直线形、X形和双弧形三种均压槽结构，通过仿真计算得到不同结构下气膜的压力分布与轴承的气体质量流量，利用差膜计算的方法，得到轴承相应的承载力、刚度和气体质量流量，分析了均压槽的不同结构对轴承承载能力的影响。经过计算发现，直线形均压槽对轴承的承载性能具有最佳的提升效果，之后对直线形均压槽的宽度、深度以及节流孔的个数进行了优化分析，得到以下结论：

(1)增加均压槽可以有效提高轴承的承载力和刚度，直线形均压槽可以使轴承的承载力提升4.8倍以上，刚度提升3.5倍以上，并且使轴承气膜的压力分布更加均匀，压力下降更慢，提高了高压气体的利用率，但增加了轴承的耗气量。

(2)均压槽的宽度对轴承的承载力、刚度和质量流量的影响基本可以忽略；当偏心率较小时，适量增加槽深可以提高轴承的承载力和刚度，减少轴承的耗气量。

(3)增加节流孔的个数可以提高轴承的承载力，但会导致轴承的刚度减小，并且增加轴承的耗气量。