基于改进的LSTM的工业机器人柔性关节迟滞建模*

党选举，刘 帆

(桂林电子科技大学电子工程与自动化学院，广西 桂林 541004)

0 引言

工业机器人具有重复精度高、自动化、安全且适用性强等优势[1]。在智能制造的背景之下，工业机器人的性能越来越强[2]，同时对工业机器人的执行精度提出更高的要求。近年来，出现的轻型机器人、协作机器人等机器人采用谐波驱动器驱动关节运动。由电机与谐波减速器等组成的柔性关节所表现出的复杂非线性迟滞特性[3-4]，直接影响工业机器人定位精度。对柔性关节的非线性迟滞特性进行建模，从控制角度，基于迟滞模型，通过补偿控制削弱其迟滞特性的影响，成为一个重要研究课题。

基于模型的柔性关节补偿控制，降低迟滞特性对定位精度的影响，建立迟滞模型是实现补偿的先决条件。国内外学者关于压电陶瓷等对象的迟滞特性建模，提出了多种方案：如Bouc-Wen模型[5]、Preisach模型等。这类模型结构较复杂，逆模型不易求解，且参数在线计算困难，难以在实时控制系统中实施。

许多学者利用神经网络模型，描述迟滞现象。文献[6]通过引入迟滞算子构建BP神经网络模型，对压电陶瓷的迟滞特性建模。文献[7-8]采用最小二乘法多项式拟合结合神经网络的方法，针对多迟滞环，需通过增加多项式的项数，保证模型精度，使模型结构更复杂。文献[9]提出了基于Preisach模型的深度学习网络的方法，建立迟滞模型，由Preisach模型特点所决定，为了覆盖到所有的工作点，在神经网络模型中必须采用更多隐含节点，使迟滞模型结构变得复杂。

以上大都是针对压电陶瓷等对象，进行迟滞建模，而工业机器人柔性关节迟滞特性所表现出的复杂强非线性，对所建立的迟滞模型在非线性特性、结构简洁等方面提出更高的要求。

LSTM能够保存和传递长时间的信息，具有记忆特性[10]。本文考虑到工业机器人柔性关节的输出与历史输入有关的记忆特性，采用了具有长期记忆特点的LSTM，对工业机器人柔性关节所表现出的复杂非线性迟滞特性进行建模。为了进一步提高建模精度，本文提出了基于改进的LSTM的工业机器人柔性关节迟滞建模方法。

1 LSTM迟滞模型

1.1 LSTM单元

为了解决传统RNN网络中存在的梯度消失与梯度爆炸问题，采用了一种特殊的RNN单元：LSTM用以代替RNN中的隐含层神经元。LSTM单元基本结构[11]如图1所示。

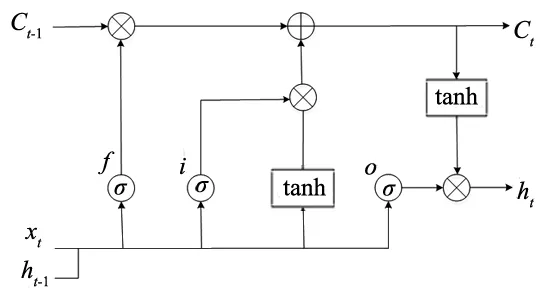
图1 LSTM单元基本结构图

其数学模型如下：

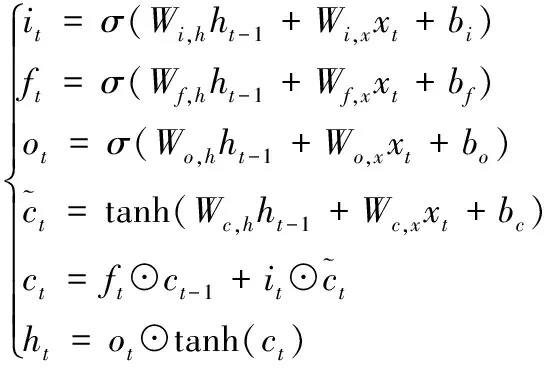
(1)

1.2 LSTM迟滞模型的构建

考虑到迟滞表现为与输入信号历史值有关的记忆特性，所以，本文先利用具有记忆特性的LSTM构建工业机器人柔性关节的迟滞模型。LSTM迟滞模型如图2所示。

图2 LSTM迟滞模型

(2)

(1)数据采集

本文搭建的工业机器人柔性关节实验平台是由安川GP7机械手、编程示教器、控制器、外部计算机等组成。

在柔性关节做往复运动时，在不同的运行速度下，工业机器人柔性关节表现出不同的迟滞特性。本文通过与工业机器人控制器通信的外部计算机，对机器人往复运动时的柔性关节转矩及角度数据实时采集。表现出不同迟滞特性曲线的两组数据，用于验证提出的LSTM迟滞模型建模精度及泛化能力：第一组数据设定关节运行最大速度为0.55 rad/s，第二组数据设定关节运行最大速度为1.1 rad/s。

(2)LSTM迟滞模型建模与验证

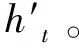
(3)

其中，yt为t时刻工业机器人柔性关节输出角度。

输出层的权值学习：

(4)

LSTM迟滞模型的输入门的权值学习：

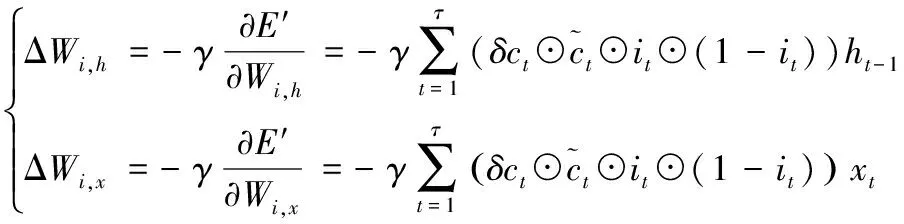
(5)

LSTM迟滞模型的遗忘门的权值学习：

(6)

LSTM迟滞模型的输出门的权值学习：

(7)

LSTM迟滞模型的输入单元状态的权值学习：

(8)

隐含层输出ht与记忆单元ct的梯度误差为：

(9)

LSTM迟滞模型的权值的更新：

Wt=Wt-1+ΔWt

(10)

其中，γ为学习速率；W代指LSTM迟滞模型中所有的网络权值。

图3 LSTM迟滞模型的建模输出 图4 LSTM迟滞模型的验证输出

图3为LSTM迟滞模型的建模输出、图4为LSTM迟滞模型的验证输出。由图3和图4可知，在LSTM迟滞建模与验证中，LSTM迟滞模型的输出曲线与工业机器人柔性关节的输出曲线存在幅值方面的差异以及相位的滞后性。针对该问题，提出了一个改进的LSTM迟滞模型。

2 改进的LSTM迟滞模型

为了对LSTM迟滞模型的输出信号在幅值和相位上进行补偿，对LSTM进行改进，在LSTM迟滞模型后串联一个RBF动态神经网络，称为改进的LSTM迟滞模型。

2.1 RBF动态神经网络

RBF神经网络具有计算量少、学习速度快、学习方法简单等优点，同时具有良好的数据局部逼近能力以及泛化能力。改进的LSTM神经网络结构如图5所示。

图5 改进的LSTM神经网络结构图

图5中，RBF动态神经网络是一种三层前馈神经网络：输入层、隐含层和输出层。输入信号为：

(11)

其中，yt-1为工业机器人柔性关节的前一时刻的角度。

RBF动态神经网络模型如下：

(12)

(13)

根据文献[12]，当损失函数过大时，RBF动态神经网络通过梯度下降法调整网络权值。网络的损失函数为：

(14)

网络权值调节：

(15)

其中，η为学习速率，α为动量因子。

2.2 改进的LSTM迟滞模型及参数学习

所提出改进的LSTM迟滞模型及参数学习如图6所示，由两部分串联组成：第一部分是LSTM迟滞模型，模型输入为柔性关节的转矩xt；第二部分是RBF动态神经网络，在RBF输入信号中加入柔性关节前一时刻的输出值，使神经网络具有动态特性。

图6 改进的LSTM迟滞模型

3 改进的LSTM迟滞模型验证

用两组数据，对所提出的改进的LSTM迟滞模型进行验证，并与LSTM迟滞模型比较。在改进的LSTM迟滞模型中，LSTM隐含层节点取10个，RBF隐含层节点取10个。

3.1 LSTM迟滞模型建模与验证

基于LSTM迟滞模型，对采集到的工业机器人柔性关节的第一组数据建模。建模效果如图7所示。图8为对应建模误差，其建模的最大绝对误差和均方误差分别为1.545 7°和0.226 3。

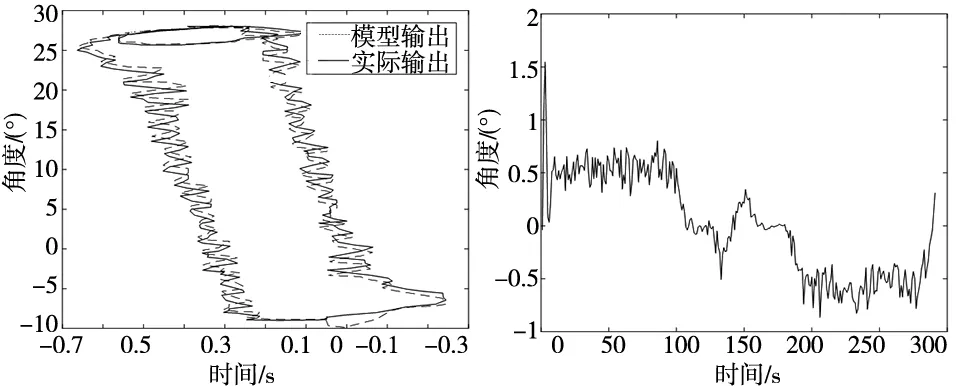
图7 LSTM迟滞模型的建模 图8 LSTM迟滞模型的建模误差

为了验证LSTM迟滞模型的适应性能力，用第二组数据对迟滞模型进行验证。

图9为LSTM迟滞模型验证效果，图10为对应验证误差，其最大绝对误差和均方误差分别为1.881 7°和1.174 0。

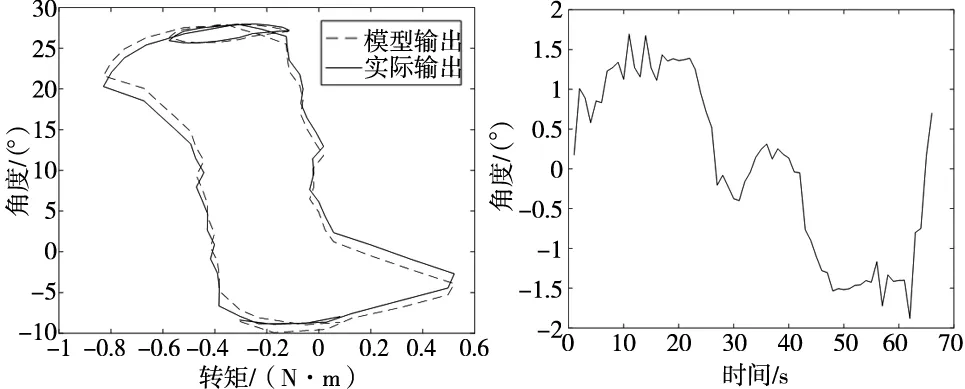
图9 LSTM迟滞模型的验证 图10 LSTM迟滞模型的验证误差

3.2 改进的LSTM迟滞模型建模与验证

基于改进的LSTM迟滞模型，对采集到的工业机器人柔性关节的第一组数据进行建模。图11为建模效果，图12为对应建模误差，其模型的最大绝对误差和均方误差分别为0.776 8°和0.024 7。

图11 改进的LSTM迟滞模型的建模 图12 改进的LSTM迟滞的建模误差

为了验证改进的LSTM迟滞模型的泛化能力，用第二组数据对迟滞模型进行验证。

验证效果及验证误差如图13、图14所示。改进后的迟滞模型验证的最大绝对误差和均方误差分别为1.218 0°和0.064 3。

图13 改进的LSTM迟滞模型的验证 图14 改进的LSTM迟滞模型的验证误差

3.3 实验数据仿真结果比较与分析

迟滞模型的建模均方误差和验证均方误差的对比如表1所示。实验数据仿真结果表明，LSTM迟滞模型基本可以描述出工业机器人柔性关节的非线性迟滞关系，但在相位上存在滞后误差，尤其在模型验证中滞后明显。改进的LSTM迟滞模型的建模精度与验证精度都高于改进前的LSTM迟滞模型。

表1 模型的均方误差

4 结论

针对工业机器人柔性关节的复杂非线性迟滞特性，为了得到高精度迟滞模型，从造成模型误差的幅值与相位两个角度考虑，对人工智能中的长短时记忆模型(LSTM)进行改进， 将LSTM迟滞模型与RBF动态模型相融合，构建了一个改进的LSTM迟滞模型。实验数据仿真结果表明，与LSTM迟滞模型比较，改进的LSTM迟滞模型，对工业机器人柔性关节迟滞特性建模，具有更高的精度和泛化能力，为基于模型的工业机器人柔性关节高精度补偿控制，提供了基础。