基于改进动态窗口法的移动机器人避障研究*
常新新,胡 为,姬书得,岳玉梅
(沈阳航空航天大学 a.航空宇航学院; b.自动化学院,沈阳 110136)
0 引言
自主避障[1-3]是移动机器人领域研究的重点及热点问题。DWA算法[4-5]根据机器人的动力学与运动学特性得到一系列速度的离散值,然后用这些速度模拟接下来一段时间内机器人的轨迹,并采用评价函数评价这些轨迹,选取得分最高的轨迹对应的速度作为下一阶段的速度。DWA算法在每一阶段需要评价的轨迹数目较多,增加了避障时间,而且在评价轨迹时,权重参数的选取不当容易导致机器人在密集障碍物区无法选择最佳路径的问题[6]。文献[7]提出了一种改进的DWA算法,通过引入代价函数,使用线性回归模型对避障路径成本进行估计,选择较为合理的避障路径。文献[8]针对DWA算法,提出一种新的筛选允许速度的方法,针对非直接碰撞轨迹,在其终点处以其速度方向做射线,将与障碍物不相交的轨迹对应的速度设为允许速度。该方法考虑了预轨迹终点速度的方向,避免了部分可用速度被舍弃,使得机器人能够选择较合理的速度快速通过障碍物密集区。
针对DWA避障算法存在的问题,本文提出一种较优方位角范围约束,即在模拟出预轨迹后,依据计算准则计算出较优方位角范围,然后选取出下一时刻在较优方位角范围内的预轨迹,最后通过轨迹评价函数确定最优轨迹对应的速度。该方法在原算法的基础上进一步优化了允许速度的空间,一定程度上减少了需要评价的轨迹数目,减弱了权重参数在原算法中选择最优速度时的决定性作用,提高了避障规划的效率。
1 DWA算法
1.1 DWA算法简介
DWA算法是基于机器人运动学与动力学理论的一种局部避障[9]算法,它将对机器人的位置控制转换为对机器人的速度控制。DWA算法可以概括为三步:一是根据机器人自身的限制以及环境制约将速度的采样空间约束在一定范围内;二是根据机器人运动学对采样后的速度进行模拟得到预轨迹;三是设定评价函数对预轨迹进行评分以获取最优轨迹对应的执行速度。
1.1.1 速度采样空间[10-11]
根据机器人自身最大速度和最小速度限制,速度Vs(v,w)(v表示机器人的线速度,w表示机器人的角速度)满足:
Vs={(v,ω)|vmin≤v≤vmax,ωmin≤ω≤ωmax}
(1)
考虑到机器人驱动力的约束,存在最大的加减速限制,进一步将速度空间进行约束,用Vd表示。假设机器人当前线速度为Vc,当前角速度为ωc,时间间隔为t,则下一时刻的可达速度Vd(v,w)满足如下条件:
(2)
基于移动机器人的安全考虑,为了能够在碰到障碍物前停下来,因此在最大减速条件下,速度满足:
(3)
式中,dist(v,ω)为速度(v,ω)对应轨迹上离障碍物最近的距离。该碰撞条件是在机器人轨迹模拟出来之后,根据机器人与障碍物之间的距离,然后计算当前采样的速度能否在碰到障碍物之前停下,如果能够停下来,该速度就是允许的速度。
机器人最终的速度采样空间为:
Vr=Vs∩Vd∩Va
(4)
1.1.2 速度采样及轨迹生成
人为设定速度采样的线速度分辨率以及角速度分辨率,得到所有速度组合。根据机器人运动学模型对采样的速度进行模拟,得到一系列下一时刻的预轨迹。
1.1.3 轨迹评价
采样的速度中,不止一组速度对应的轨迹是可行的,为了获取最优的执行速度,采用评价函数对每条轨迹进行评价。评价函数定义为:
G(v,w)=σ(α·heading(v,w)+β·dist(v,w)+γ·velocity(v,w))
(5)
式中,使得G(v,w)值最大的速度为最优速度;函数项heading(v,w)中heading=π-φ(φ表示用来评价机器人在当前设定的采样速度下,达到模拟轨迹末端机器人的航向与目标线的夹角),如图1所示。

图1 机器人方位角
函数项dist(v,w)用来评价机器人在当前轨迹上与最近的障碍物之间的距离,若这条轨迹上没有障碍物,则设定一个常数;函数项velocity(v,w)评价当前轨迹对应的速度大小,速度越大的评分越高;α,β,γ为3个参数,代表每一个函数项的权值。
待评价项heading(v,w)、dist(v,w)和velocity(v,w)计算出来后,需要做归一化处理,然后再相加,归一化的准则是每一项除以每一项的总和。即:

(6)
式中,i为待评价的当前轨迹点,n为采样的所有轨迹点。
1.2 改进的DWA算法
本文提出一种改进的DWA算法,在模拟出下一时刻的预轨迹后首先根据计算准则确定机器人前进的较优方位角范围,然后选取出较优方位角范围以内的预轨迹,最后通过轨迹评价函数确定最优轨迹对应的速度。
当机器人前进方向上有多个障碍物时,根据机器人携带的单线激光雷达观测到的障碍物的方位信息,计算可通行的较优方位角范围。具体步骤如下:
(1)坐标系转换
为方便计算,将激光雷达坐标系原点与机器人坐标系原点重合,建立机器人极坐标系以及全局坐标系,将机器人的方位角变换到全局直角坐标系下。如图2所示,机器人在全局坐标系下的方位角为α,β为极坐标系与全局坐标系的变换角。
β=α-90°
(7)
已知机器人极坐标系下终点的方位角为φ,则在全局坐标系下的方位角为φ1,表示为:
φ1=φ-β
(8)
式(8)为机器人方位角由极坐标系转换到全局坐标系下的转换公式。

图2 坐标转换图
(2)可通行区域判定
如图3所示,在机器人极坐标系下,以θ2角度区域为例,如果相邻障碍物间的距离c≥dr(dr为机器人的宽度),则可判定该区域为可通行区域[12],否则为不可通行区域。图4中a和b分别为机器人到障碍物A与障碍物B的距离,由余弦定理可得,两障碍物间的最近距离c为:
(9)

图3 可通行区域判定
(3)较优方位角范围确定
在机器人运行环境已知的情况下,当机器人距离目标较远时,为避免机器人转动太大角度,优先考虑与机器人航向较近的可通行区域,因此将机器人当前航向与可通行区域夹角较小的方位角范围设为较优方位角范围;反之,当机器人与目标点距离较近时,将目标线与可通行区域夹角较小的方位角范围设为较优方位角范围。
由于机器人在躲避障碍物过程中行走的路径不规则,机器人与目标点的距离可能不会呈单调递减趋势,因此设定距离准则以描述机器人距离目标点的远近。如图4所示,在全局坐标系下,机器人初始y坐标为y0,以机器人和目标点在y方向的坐标差描述两者距离的远近。较优角度区域的计算准则为:

(10)
yG-y0表示目标点和机器人起始点在y方向的坐标差;yr-y0表示机器人某时刻y方向的坐标与起始点y坐标的差值。

图4 机器人与目标点的距离准则
较优方位角范围确定方法如下:
情景1:当机器人与目标方向较远时,计算机器人当前航向与可通行区域夹角较小的方位角范围。如图5所示,在极坐标系下,机器人共有4个可通行的候选方位区域:θ1,θ2,θ3,θ4,其中与机器人当前位置最接近的角度区域为θ2和θ3。θ2和θ3均为机器人下一时刻的可通行区域,通过比较θ2和θ3区域与目标线的角度差β1和β2,可知β1>β2。因此可将与航向较近的θ3区域设为机器人前进的较优方位区域。
θ3角度区域的起始为γ1,终止角度区域为γ2,转换到全局直角坐标系下表示为:
(11)
即机器人下一时刻前进的较优方位角范围为[γ1-β,γ2-β]。
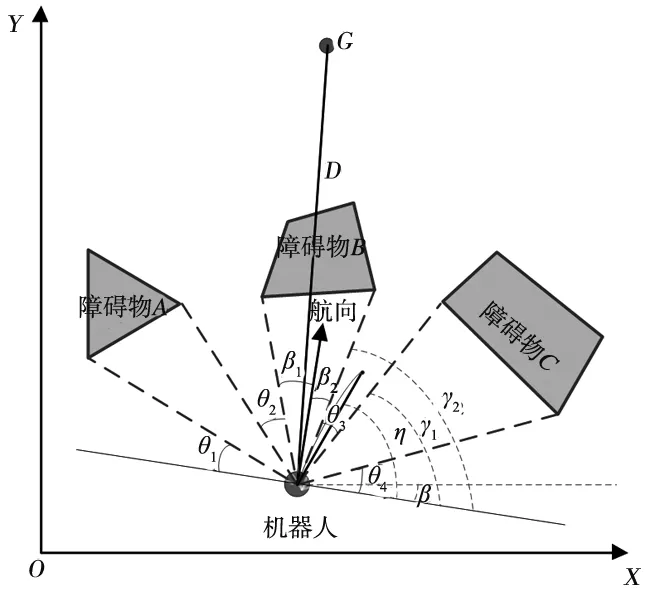
图5 机器人航向与可通行区域关系示意图
假设机器人坐标系下,预测轨迹的终点的方位角为η,预测轨迹的终点和机器人当前位置的连线与较优角度区域边界的夹角满足:

(12)
情景2:当机器人与目标点距离较近时,计算目标线与可通行区域夹角较小的方位角范围。同理,由图6可知,通过计算,θ2和θ3均为可通行的区域,通过比较θ2和θ3区域与机器人航向的角度差β3和β4,可知β3<β4。因此可将与目标点较近θ2区域设为机器人前进的较优方位区域。
θ2角度区域的起始为γ3,终止角度区域为γ4,转换到全局直角坐标系下表示为:
(13)
即机器人下一时刻前进的较优方位角范围为[γ3-β,γ4-β]。

图6 目标线与可通行区域关系示意图
此时预测轨迹的终点和机器人当前位置的连线与较优角度区域边界的夹角满足:

(14)
改进后的DWA算法步骤如下:
(1) 根据传感器信息,得到机器人与障碍物的距离及方位,确定可通行区域;
(2) 根据机器人的动力学与运动学特性以及机器人当前速度和加速度,在速度采样空间中对v与ω进行离散采样,得到一系列速度(v,ω);
(3) 根据机器人运动学特性对采样的速度进行模拟,进而得到一系列预轨迹。根据以上准则及方法计算下一时刻机器人前进的较优方位角范围,剔除较优方位角范围以外的轨迹对应的速度;
(4) 采用评价函数对剩余的轨迹进行评价,首先将评价项按照式(6)的方法进行归一化处理,然后根据式(5)求出评价得分最高的一组轨迹对应的速度(v,ω)作为下一时刻的执行速度。
(5) 执行最优速度,判断是否到达目标点,若是,则结束运行;若否,则返回第一步,进入下一步循环。
2 改进的DWA算法仿真实验
对原DWA算法以及改进的DWA算法进行仿真,仿真环境为MATLAB 2019b,并对结果进行分析。DWA算法涉及了机器人自身的多个参数以及算法参数,选取的参数如表1和表2所示。

表1 机器人自身参数

表2 原DWA算法参数
为了充分证明改进的DWA算法的可行性以及避免算法适用环境的偶然性,本文设计了两种机器人运行环境,并进行仿真实验,如图7、图8所示,验证在不同环境下,改进的DWA算法在局部避障中的可行性及优势。
在仿真时,将机器人当作质点处理,但是在实际运行中,机器人是有一定体积的,因此采用障碍膨胀处理的方法将机器人的尺寸考虑到障碍物上,仿真中采取的障碍物膨胀半径为0.4 m。两种运行环境中机器人起点分别为(0,0)和(12,0),目标点分别为(12,14)和(0,14),为便于区分对比,将原DWA算法实验的路径轨迹设置为蓝色,将改进的DWA算法实验的路径轨迹设置为绿色。由原DWA算法仿真的轨迹图可知,机器人在运行过程中容易陷入局部最优,而且在密集障碍物区选择的路径不是最佳路径,规划的避障路径相对较远,若在实际运行中可能会增加机器人遇到动态障碍物的概率,从而降低运行的效率。由改进后的DWA算法仿真结果可以观察出,两种不同的运行环境下,机器人在密集障碍物区能够选择较优方位角区域的速度运行,机器人付出的的代价较小,而且运行后的轨迹较为平滑。

(a) 原DWA算法仿真轨迹图 (b) 改进的DWA算法仿真轨迹图图7 运行环境1

(a) 原DWA算法仿真轨迹图 (b) 改进的DWA算法仿真轨迹图图8 运行环境2
对算法改进前后的迭代次数与运行时间进行定量分析,如表3所示。由于运行环境设置的复杂性以及时间分辨率较低等因素,导致避障中算法迭代的次数较多、运行时间比较长。但在参数设置相同的情况下,改进后的DWA算法迭代次数相比原DWA算法要少,减少了需要评价的轨迹数目,而且运行所用的时间少,在避障效率上有所提高。

表3 改进前后迭代次数与运行时间对比
3 结论
本文通过改进DWA算法对移动机器人避障效果进行优化,针对DWA算法提出了一种较优方位角范围约束及其计算准则优化允许速度空间。改进后的DWA算法在一定程度上减少了需要评价的轨迹数目,减弱了原算法中权重参数对最优轨迹的决定性作用。仿真结果表明:在密集障碍物区,采用改进的DWA算法,机器人能够以最佳路径选择较优的区域通过,避障效率得到提高。本文只是将改进的DWA算法在仿真环境下进行了避障规划实验,下一步将进行实物实验验证改进算法的有效性。

