BAS-LSA混合算法在装配序列规划的应用*

任 云，刘 丹

(贵州大学现代制造技术教育部重点实验室，贵阳 550025)

0 引言

装配是生产制造的重要环节，直接关系到产品质量、性能、寿命和可维护性，装配序列规划是装配工艺规划的重要部分，序列的优劣直接影响装配质量[1]。装配序列规划研究可以优化装配顺序，使企业获得生产成本更低、装配效率更高、质量更佳的装配方案。装配序列规划是一个典型的非确定性多项式(Non deterministic polynomial,NP)组合优化问题[2]，产品的装配序列数量与产品的零部件数量呈指数增长关系，越复杂的产品越容易遇到装配序列组合爆炸问题[3]，这给装配规划问题带来了很大的挑战。

为了更好解决这一问题，研究者将各类智能优化算法如遗传算法[4]、蚁群算法[5]、模拟退火算法[6]、神经网络算法[7]等应用到装配序列规划中，这些算法在一定程度上克服以往方法中存在的组合爆炸问题及装配的局限问题。遗传算法是目前在装配序列规划中应用最为广泛的算法，但遗传算法要求初始种群为可行序列，且全局收敛速度慢和存在大量重叠迭代的问题；蚁群算法在装配序列规划问题中也有广泛的应用，但它运算效率较低，且开始阶段信息素积累较慢，容易陷入局部最优[8]，针对上述问题，论文根据装配序列规划问题的特点，提出将闪电搜索算法和天牛须算法运用于装配序列规划之中。

闪电搜索算法(Lightning Search Algorithm,LSA)是Shareef H等受自然天气中闪电现象的启发提出的一种优化算法[9]，Dorigo M等将其应用于函数优化和TSP(Traveling Salesman Problem)问题[10]，并取得了良好的优化效果, Islam M M等提出了一种基于二进制编码的闪电搜索算法[11]，证明了该算法在搜索精度和收敛性方面性能表现良好。

由于LSA算法模拟闪电的快速传播特性，因此收敛速度较快。但LSA算法本身存在求解精度不高、易陷于局部最优等缺点。

天牛须搜索算法(Bettle Antennate Search Algorithm,BAS)在2017年由Jiang X等根据天牛个体用左右触须感受食物气味的方向逐渐接近食物这一特点提出的[12]。研究表明BAS算法在搜索速率与搜索精度上均可达到理想的结果。BAS算法局部搜索能力很强，但全局搜索能力不足。因此，本文结合天牛须搜索算法和闪电搜索算法的优点，提出将天牛须搜索算法和闪电搜索算法混合的装配序列规划优化方法,以此来解决闪电搜索算法容易陷入局部最优的问题，提高跳出局部最优的能力和搜索精度。

1 BAS和LSA的基本原理

1.1 LSA算法的基本原理

闪电搜索算法(LSA)是对闪电这种自然现象的观察而得到的新新算法，当闪电形成时，空气中的“放电粒子”与空气碰撞之后会产生一条电离路径或通道，并形成一条梯级先导。LSA算法利用空间放电体、和引导放电体等概念建立分布函数模型来求解待解决的问题[13]，空间放电体试图成为最优梯级先导，引导放电体代表种群中的最优个体[14]。

(1)在一个种群规模为N，初始种群的生成服从均匀分布，创建初始随机种群，其概率密度函数f(xc)可以表示为：

(1)

式中，xc是一个候选解，a和b分别是“放电粒子”范围的最小值和最大值。

(2)引导放电体表示为HL，由正态概率密度函数f(xk)来生成位置：

(2)

式中，μ为形状参数，引导放电体HL在下一次迭代的位置为：

(3)

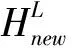
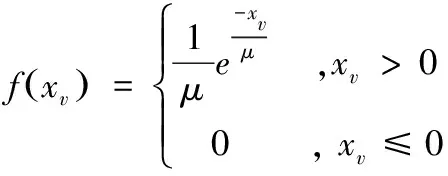
(4)

形状参数μ会影响CS和HL之间的距离，CS在下一次迭代的位置为：

(5)

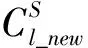
(4)分叉是放电体的另一特性，在LSA算法中分叉有两种方式，首先分叉会形成两个互相对称的通道：

rl=e+g-rl

(6)

其中，e和g表示边界，rl和rl分别表示原来的通道和分叉产生的对称通道。为了保证种群大小不变，两通道只保留一个。

1.2 BAS算法的基本原理

天牛须搜索算法(BAS)是一种新的启发式算法，它的特点是仅有一个天牛个体，所以运算速度很快，计算量低。

BAS算法的基本原理为：天牛个体在寻找食物的过程中通过左右触须来感受食物的强度，因为两须的位置不一样，所以两须所探测的强度也不一样，天牛最终朝强度更大的触须所指的方向前进一步，不断重复上述流程，直到找到食物的具体位置。其中食物气味相当于寻优函数，食物的具体位置相当于寻优函数的最优解。根据天牛的觅食过程抽象出的BAS算法遵循如下原则[15]：①天牛在物理世界寻找食物的过程可以到虚拟天牛在任意维空间求解函数最优值的情形；②天牛左右两触须对称；③天牛每次向前移动的距离与两须之间的距离成比例；④天牛每次前进后身体的方向不确定[16]。

根据以上原则，BAS 算法的数学表达如下：

(1)假设随机产生的天牛方向为d，质心位置为x，右边触须位置为xr，左须为xl，两须之间的距离为m，mt表示天牛在t时刻的两须之间的距离，根据天牛的方向可以计算出左须和右须的位置：

xr=xt+dtb

(7)

xl=xt-dtb

(8)

(2)计算适应度值f(xl)和f(xr)的大小，比较两者的大小，再决定天牛下一步的走向：

xt=xt-1+δtbsign(f(xr)-f(xl))

(9)

其中，xt为t时天牛的位置，sign为符号函数；δ为搜索步长，其大小是一个随时间t逐渐衰减的函数值。t时刻的m与δ可表示为：

dt=etad*dt-1+0.01

(10)

δt=etaδ*δt-1

(11)

其中，eta_m和eta_δ分别为两须之间的距离和步长的递减系数，通常小于1。

(3)判断求解结果是否达到理想的精度或迭代次数超过最大迭代次数，满足一个条件就完成迭代，否则重复式(7)～式(10)的步骤。

2 装配关系模型的构建

由于机械产品的装配具有多种装配方案，零件装配序列有多种选择，这增加了产品的复杂性，影响装配时间、装配成本以及装配质量的因素有很多种，其中零件的几何可行性、装配方向、装配工具的改变次数、零件之间的稳定性是主要影响因素，所以本文将以上4个因素作为评价指标。

2.1 几何可行性

在装配体上装配零件Pi时，须考虑当前零件的装配可行性，即Pi从无穷远处沿方向v装配时，前i-1个零件对Pi是否干涉。须首先构建6个方向的干涉矩阵[17]，如式子(12)所示，其中Pij表示零件j在装配时零件i对零件j的干涉，有干涉Pij=1，无干涉Pij=0。并根据式(13)、式(14)判断零件的装配可行性。

(12)

(13)

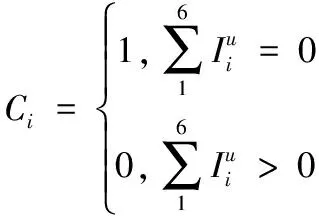
(14)

式中，n为装配序列零件的个数，u为±X，±Y，±Z的一个方向，Ci=0表示零件pi装配时会发生干涉，Ci=1中表示在某一方向上装配是可行的。

2.2 连贯性

连贯性是指零件装配过程中，相邻零件Pi与Pi-1装配方向是否相同。对于比较复杂的装配体，装配方向的改变会增加装配难度，加大了对装配工具的要求，同时还会明显增加装配时间和成本。由式(15)判断零件pi与pi-1的装配方向是否相同。

(15)

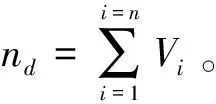
2.3 一致性

一致性是指装配相邻两个零件时使用相同的装配工具，如装配零件的前后装配工具不相同，中途还需更换装配工具，这也增加了装配的步骤，应尽量减少装配过程工具的装换次数，由式(16)判断装配工具的装配次数。

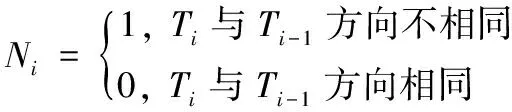
(16)

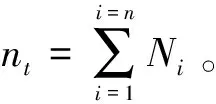
2.4 稳定性

稳定性是指装配零件pi时，前一个零件pi-1对pi是否有支撑作用，如没有支撑作用，则还需额外的支撑工具支撑pi的装配，这就给装配过程带来额外的工作量，因此零件装配过程需要考虑零件pi-1对pi的支撑作用，提高装配效率，由式(17)评价装配序列的稳定性。

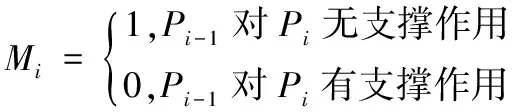
(17)

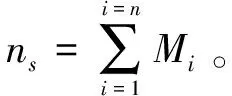
2.5 适应度函数

适应度函数通过从几何可行性、连贯性、一致性、稳定性4个方面来评价序列。适应度函数如式(18)所示：

F(n)=w1*ng+w2*nd+w3*nt+w4*ns

(18)

其中，n为种群中第n个序列，ng为一条序列干涉次数之和，nd为装配方向的改变次数，nt为装配工具的改变次数，ns为无支撑作用的次数；w1、w2、w3、w4为权重系数；其中一条可行装配序列的干涉次数应该为0，即ng=0，F越小表明这条序列越优。

3 LAS-BAS混合算法改进及步骤

LSA算法有求解精度低、容易陷入局部最优的缺点。BAS算法在全局的搜索能力较弱，且个体具有单一性，但局部搜索能力很强的特点，考虑将每一代经LSA求解的种群中不满足几何可行性的个体作为一个天牛须粒子以天牛须算法进行优化，提高LSA跳出局部最优的能力和搜索精度。

步骤1：设置算法的初始参数：最大迭代次数Nmax、种群规模N、梯级先导尖端能量El和最大通道时间T。

步骤2：生成随机初始种群，计算放电体能量Ep和目标函数值大小。

步骤3：开始循环，更新梯级先导尖端能量El，找到最差、最优梯级先导。

步骤4：通道时间每次加一，如达到最大通道时间T，则淘汰适应度值最差的通道并重置通道时间。

步骤5：更新放电体方向和能量Ep，并计算引导放电体和空间放电体适应度值。

步骤6：计算放电体能量Ep，如果Ep>El，那么进入步骤6.1，否则进入步骤6.2；

步骤6.2：放电体的位置保持不变。

步骤7:计算种群中个体的几何可行性，对于不满足几何可行性的个体，用天牛须搜索算法进行优化，并计算经优化后的个体适应度值，如果更优则替代当前个体，否则个体不变。

步骤8：如果迭代次数达到最大迭代次数，即结束迭代，进入步骤9，否则转到步骤3，继续增加迭代次数和通道时间，继续迭代；

步骤9：得到最优先导，输出最优解x。

根据上述步骤，LSA的基本流程如图1所示。

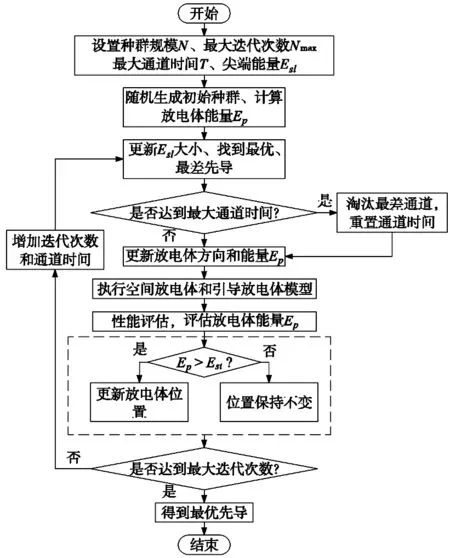
图1 LSA-BAS算法流程图

4 实例验证及分析

如图2所示，本文以蒸汽发动机引擎为例来进行算法验证。该装配体共包含18个零件。算法在MATLAB平台上编写，选择的最大迭代次数Nmax为200，种群规模N为20。为了考察闪电搜索算法—天牛须搜索算法(LSA-BAS)的优化性能，将其与差分进化算法(DE)、粒子群算法(PSO)、闪电搜索算法(LSA)相比较，比较参数为最优适应度值、最优值迭代次数、跳出局部最优的能力等方面。

本文定义一个参数Q来描述各算法逃逸出局部最优的能力，Q的数值越小表明算法的逃脱局部最优的能力越强，其中L为最大迭代次数，ΔL表示找到最优适应度值前的所有局部最优区间，max(ΔL)表示其中所有局部区间的最大区间值，如式(19)所示：

(19)

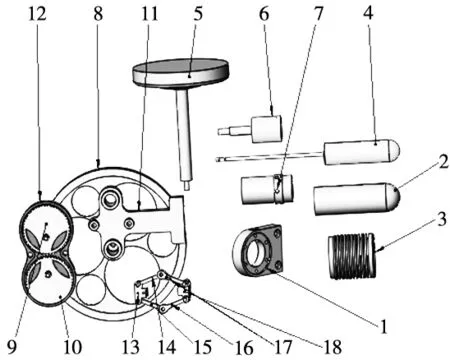
图2 蒸汽发动机引擎装配爆炸图

表1为4种算法求出的最优序列，表2对4种算法求出的装配序列几个关键评价指标：干涉次数、无支持作用次数、装配方向改变次数、装配工具的改变次数进行比较。如表2所示，各算法干涉次数皆为0，这表明所有序列都是可行装配序列，其中LSA-BAS混合算法的支撑方向、装配方向、装配工具的次数改变之和为30，是4种算法中最小的，其中差分进化算法(DE)为35，粒子群算法(PSO)为32，闪电搜索算法(LSA)为32；LSA-BAS支撑方向的改变次数为9，是4个算法中最小的，工具的改变次数为11，同样也是最小的。

表1 算法最优序列表

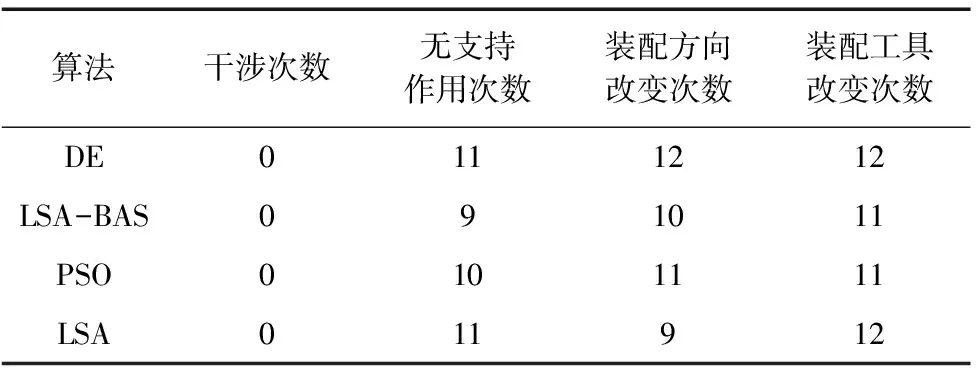
表2 装配序列及相关数值对比

表3对4种算法的性能进行了对比。如表所示，混合算法的最优适应度值为3.35，比其它3种算法的适应度值都小，找到最优值的迭代次数为109，也比其它3种算法的迭代次数小，这表明混合算法的收敛速度及搜索精度强于其它3种算法。

表4中L为最大迭代次数，图3为算法收敛曲线，从中可以得到局部最优最大区间。从表4算法局部最优对比可看出，在找到最优值迭代次数之前，混合算法陷入局部最优的最大代数为38代，Q值为0.19，远小于其它3个算法的Q值，这表明LSA-BAS混合算法逃逸处局部最优的能力远大于其它3种算法，并且最终除LSA-BAS混合算法外其它算法未能跳出局部最优，综上所述表明混合算法在求解过程中，在全局搜索能力、搜索精度及跳出局部最优方面有明显优势。

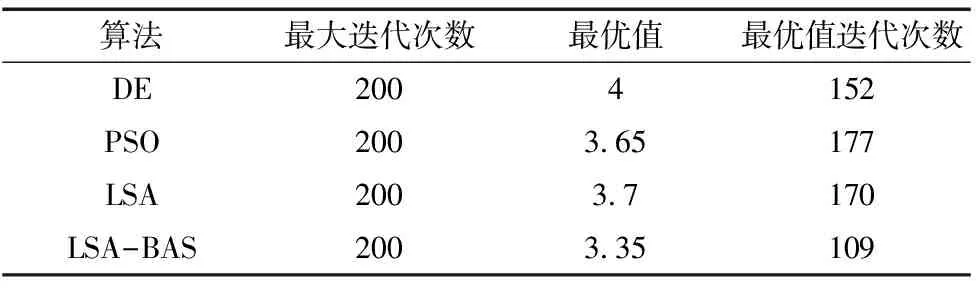
表3 算法结果对比表

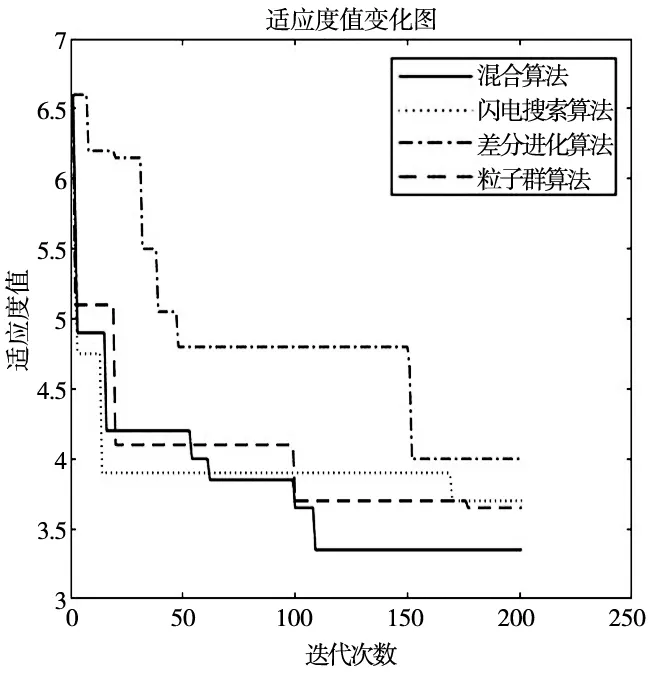
图3 算法收敛曲线

5 结论

LSA算法是一种新的元启发式算法，LSA算法在求解过程中存在收敛速度较慢、容易陷于局部最优的缺点，针对LSA算法的不足，本文首次提出了把BAS算法中天牛个体的觅食过程融入闪电搜索算法的混合算法，该算法利用BAS算法局部搜索能力较强的特点，使天牛须的感知与闪电粒子的传播过程相结合，有效的解决了闪电搜索算法易陷入局部最优的问题，加快了算法的收敛速度，提高了算法的搜索精度和全局搜索能力。通过实例验证和算法对比，该算法在解决装配序列规划问题方面具有良好的收敛性能和跳出局部最优的能力。