面向实时人群动力学分析的深度基本图网络

马 晴，康 宇,，宋卫国*，曹 洋

(1.中国科学技术大学火灾科学国家重点实验室，合肥，230026；2.中国科学技术大学自动化系，合肥，230026)

0 引言

在行人疏散动力学研究中，基本图是行人动力学分析中一项重要的工具。研究人员在临界密度、最大流量、行人自由速度等方面都有不同的研究成果。Weidmann[1]通过行人运动基本图研究发现，行人自由速度随密度增大而减小，在行人密度达到5.4人/m2时速度为0，临界密度为1.55人/m2时最大流量1.15人/m/s；但Helbing等[2]通过分析2006年麦加朝圣踩踏事故的行人运动基本图发现，在极高密度的情况下(10人/m2)，行人运动速度不为0，行人仍然可以缓慢行走，且行人密度出现第二峰值，与前人的研究结果不同；Armin Seyfrid课题组[3]在比较了不同文化背景下行人运动基本图后得到如下结论，相同密度下印度人的行走速度大于德国人；Cao等[4]分析了不同年龄人群单列实验的基本图发现，老年人的最大流量大于混合人群的最大流量。研究人员通过分析基本图获得了很多重要的行人动力学规律，因此快速准确的获得基本图有助于行人动力学研究。

目前主流获得基本图的方法是对视频中的行人进行轨迹跟踪，再计算得到基本图。其基本思想是，区分前景和背景，给定特定颜色阈值建立参考模型来提取行人运动轨迹。这种使用RGB阈值的方法虽然可以较准确的提取前景中的行人，但在行人轨迹跟踪过程中会出现目标丢失现象。

随着深度学习的发展，针对人群计数问题，研究者们提出了不同的网络结构[5-7]，这些网络的特点是采用了多列结构，即网络中包含几个子网络，子网络之间的卷积核大小不同，不同大小的卷积核可以提取不同尺寸的行人信息。网络都是在GPU上加速运行的，程序运行速度快。考虑到实时获得行人动力学信息的任务，我们提出了一种深度基本图网络。

我们的深度基本图网络结构如图1所示，网络由多尺度递归卷积神经网络(MSR-Net)和光流模块组成。MSR-Net用于获得行人密度图，MSR-Net使用多列结构，但将输出改为行人密度图以获得行人空间信息，便于进一步应用于异常检测。光流模块(OF-Net)对运动目标进行检测，可以得到行人的速度图。我们的光流模块选用LK稀疏光流法，稀疏光流运算量小、速度快，适用于我们的实时任务。通过密度图和速度图可以获得基本图。同时，通过速度图和密度图的空间对应关系还可以实现异常检测。

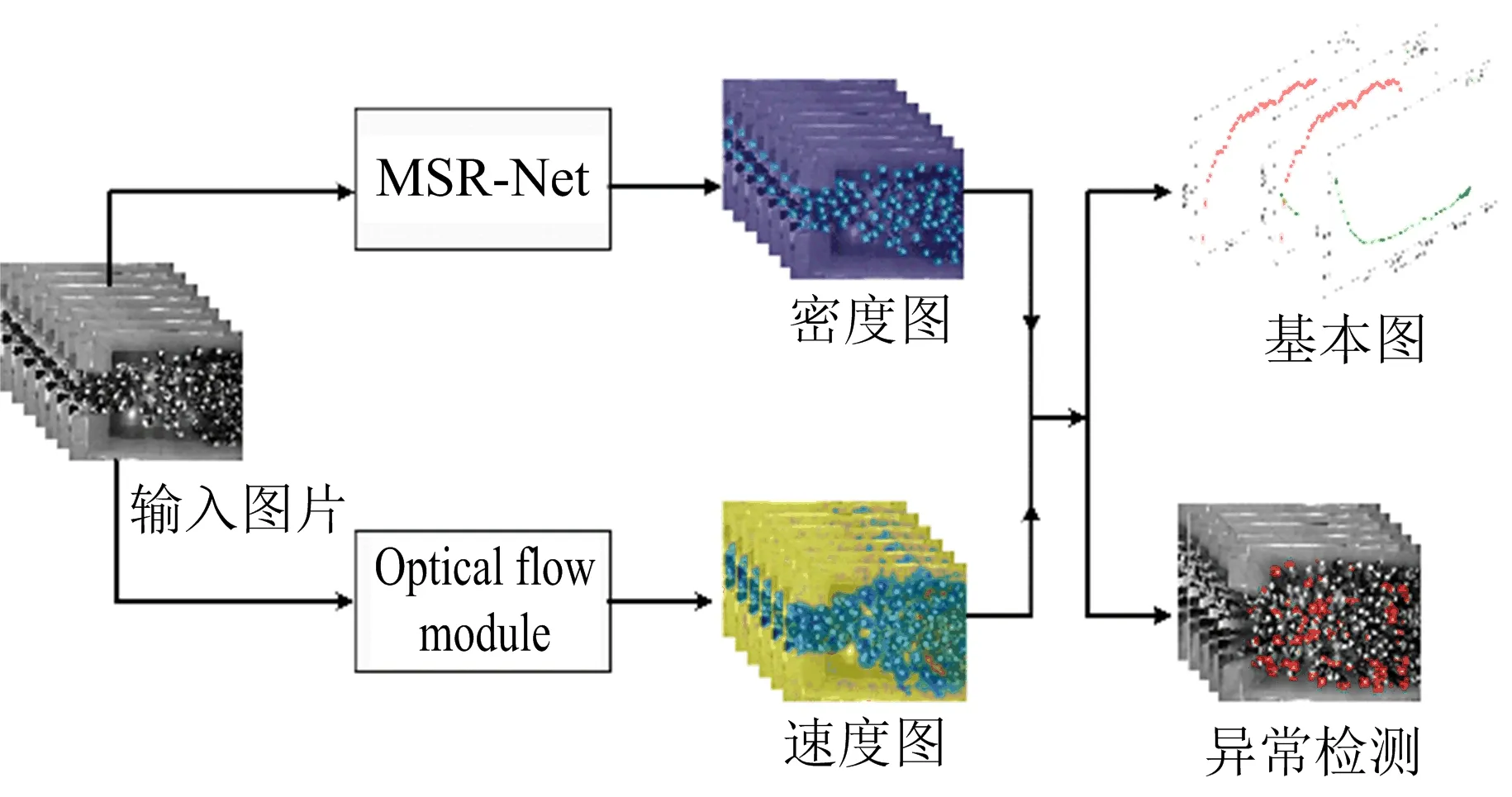
图1 深度基本图网络结构Fig. 1 The structure of the proposed deep fundamental diagram network

1 方法

我们提出的深度基本图网络由两部分组成，一部分是用于获得行人密度图的多尺度网络(MSR-Net)，另一部分是用于获得行人速度图的光流模块。下面详细介绍这两部分如何获得行人密度和速度以及通过二者空间对应关系获得基本图的方法。

1.1 多尺度递归卷积神经网络(MSR-Net)

1.1.1 准备训练数据

选取2组公开实验(UNI_CORR_500_01、UNI_CORR_500_02)[8]制作数据集，共有6 682张有效帧图像，随机选取500张图片作为测试集，剩余图片作为训练集。数据集的质量直接影响训练效果，为了获得密度图，手工标记了6 682张图像上所有行人头部的位置pi，采用2D高斯核函数生成密度图作为数据集的标签：

(1)

其中，n表示一张图像上标记的行人总数，N表示高斯核，σ表示方差。密度图的生成过程如图2所示，每个点经过高斯核变换之后的像素累加值为1，因此图2中所有像素值相加值等于实际人数C，即：

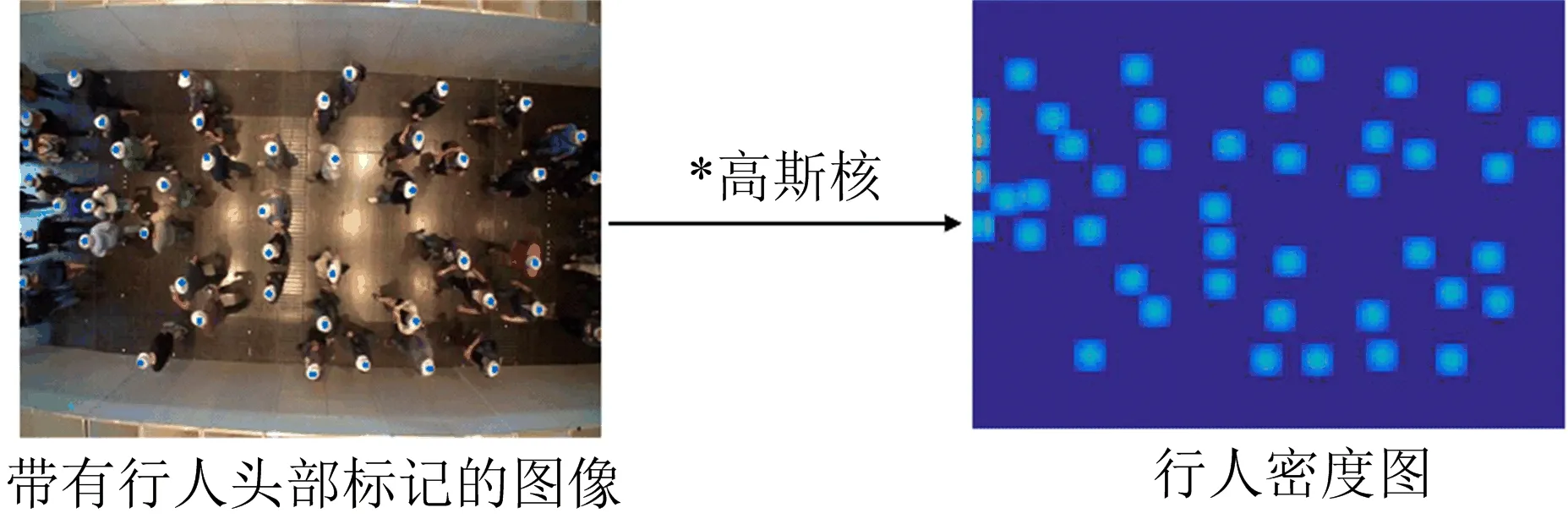
图2 行人密度图生成过程Fig. 2 Crowd density map generation process

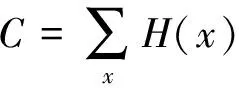
(2)

对全部6 682张带有行人头部标记的图像进行高斯变换，得到相应的人群密度图作为训练和测试标签。

1.1.2 网络结构

考虑到不同试验场景下拍摄的行人头部大小不一致的问题，我们需要一种能够提取不同尺度信息的网络结构。多列卷积神经网络(MCNN)[6]和多尺度递归卷积神经网络(MRCNN)[7]都提出了多列结构用于学习多尺度信息，多列结构由3个子网络组成，每个子网络中卷积核大小不同，在卷积运算中感受野大小不同，大的卷积核可以提取图片中大尺度纹理信息，小的卷积核可以提取到细节纹理信息，网络的输出都是行人数量。因此，我们提出了MSR-Net来提取多尺度信息，网络结构如图3所示。我们的网络保留了多列结构，多列结构中三个子网络相互独立，卷积核大小不同，用于提取不同大小头部的纹理特征。网络的融合部分(Concat)将三个子网络提取的行人不同尺度信息进行融合，相互促进和学习，让我们的网络能够提取大尺寸头部的细节特征和小尺寸头部的全局特征。递归卷积部分参数共享，在增大感受野的同时既不会丢失像素信息，又不会增加网络参数。这部分的输入是多尺度融合的输出，由于扩大了感受野，就有更多的信息交互，增加了网络表征能力。我们的网络将输出改为行人密度图，行人密度图由递归卷积部分输出特征，通过一个卷积核大小为1×1的卷积层映射而来。我们的网络所有池化层采用最大池化，激活函数选用ReLu。

图3 多尺度递归卷积神经网络(MSR-Net)结构Fig. 3 The struct of MSR-Net

1.1.3 网络训练

本文利用Caffe深度学习框架[9]对网络模型进行微调。我们的方法已经在MATLAB中实现，在3.60 GHz Intel(R) Core (TM) i7 CPU, 16G RAM的PC上运行。CNN是在GPU上运行的，我们使用NVIDIA GTX 1050ti GPU。运行系统是Ubuntu 16.04 LTS。

网络训练需要一个初始化权值，我们的网络使用标准差为0.01的高斯分布初始化权重，基本学习率1e-5，动量参数为0.9，衰减率0.000 5，选用Adam优化参数。我们使用1.1.1节制作的密度图来微调预训练好的网络，直到损失函数值不再降低就停止训练。

我们的网络输出是密度图，采用欧式距离作为损失函数，计算网络估计结果和真实结果间的差距，函数定义为：

(3)

其中，N是训练图像的个数，Xi是输入图像，Fd(Xi;Θd)表示通过MSR-Net生成的人群密度图，Di表示真实密度图，LD(Θ)表示网络估计得到的密度图与真实密度图之间的损失值。

1.2 光流模块

在我们的光流模块中，选择LK光流算法，也称为稀疏光流法[10]，与稠密光流相比计算量更小，速度更快。其中运动场景可描述为：

(4)

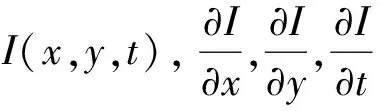
IxVx+IyVy=-It

(5)

假设相邻两帧图像位移很小，局部向量(Vx,Vy)必须满足：

Ix(qi)Vx+Iy(qi)Vy+It(qi)=0

i=1, 2, 3…,n

(6)

其中，qi为邻域内像素的个数。Ix(qi),Iy(qi),It(qi)是当前时刻图像在点qi处对x，y位置和时间t的偏导数。以矩阵形式表示为：

Av=b

(7)

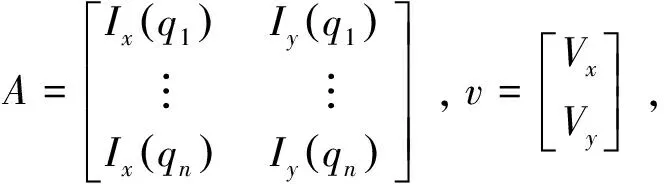
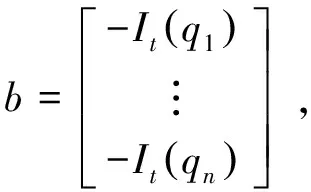
v=(ATA)-1ATb

(8)

在真实场景中的真实移动距离转换如下：

(9)

其中，d是真实实验场景中长度L包含的像素个数，x是每个像素移动的距离。每个像素的真实速度为：

(10)

其中，p是帧率。

1.3 计算基本图

1.3.1 时间-密度图

在1.1我们的网络学习了输入图像和密度图之间的映射关系，每输入一帧图像就可以得到这一帧的密度图。密度图的像素和等于行人数量，测量区域的密度可表示为：

(11)

其中d(x,y)为测量区域内(x,y)位置的像素值。N是测量区域内像素个数总和。A是测量区域的面积。这样我们就可以得到每一帧的密度，进一步得到时间-密度图。相对于轨迹跟踪的方法，每输入一帧图像我们的网络就可以输出这一帧的密度图并得到测量区域的密度，具有实时性，对于行人动力学分析更具有价值。

1.3.2 时间-速度图

输入的图片经光流模块处理后，得到一张速度图，每个像素值表示该像素真实的位移大小和方向。由于光流模块会提取到行人走路时快速摆手，对真实速度的计算产生干扰，我们需要利用1.3.1的密度图消除速度计算偏差。

首先，利用密度图对速度图的计算偏差进行校正。在行人头部的位置，密度图的像素值非零，其他位置像素值为零，可以说密度图提供了行人的定位。如图4(a)，密度图和速度图都在同一坐标系下，存在空间对应关系。如图4(b)，上下为同一帧的密度图和速度图，同时遍历两张图的所有像素，密度图像素值为0的点，速度图的同一坐标位置像素值也置为0；密度图像素值非零的点，速度图的同一坐标像素值保持不变，这样我们可以得到一张校正后的速度图。

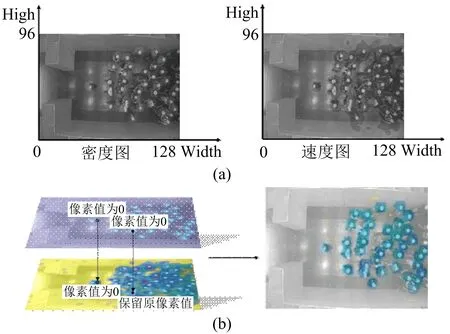
图4 (a)密度图和速度图的空间对应关系；(b)通过密度图和速度图的空间对应关系校正原有速度图，得到新的速度图。Fig. 4 (a) Correspondence between density map and velocity map; (b) The new velocity map obtained by correcting the original velocity map through the spatial correspondence between the density map and the velocity map.

然后，在这张新的速度图上，我们可以由以下公式得到被测区域内行人的平均速度：

(12)

其中，v(x,y)为测量区域内(x,y)位置的像素值。M是测量区域中值不为0的像素个数。因此，通过密度和速度两个重要的行人动力学信息，我们可以得到基本图。

我们使用的稀疏光流模块计算量小、运行速度快，可对每帧图像进行处理，无需提取图像的前景和背景，不需要跟踪每个行人就可以得到某一帧的行人速度，对行人动力学的实时分析具有实际意义。

2 实验结果和分析

本文用公开实验数据集UNI_CORR_500[8]来验证我们的方法，其中前两组实验被用来制作训练集，第三到七组实验作为验证集。所有视频的帧率为25 fps，第三到第七组实验视频分别有4 047、4 083、3 943、4 270、5 128帧有效帧(有效帧表示图像上有行人)。每个实验都包含了轨迹跟踪文件，可作为真实值与我们的结果进行对比。图5和表1为该实验数据集的场景设置和行人进入宽度设置。

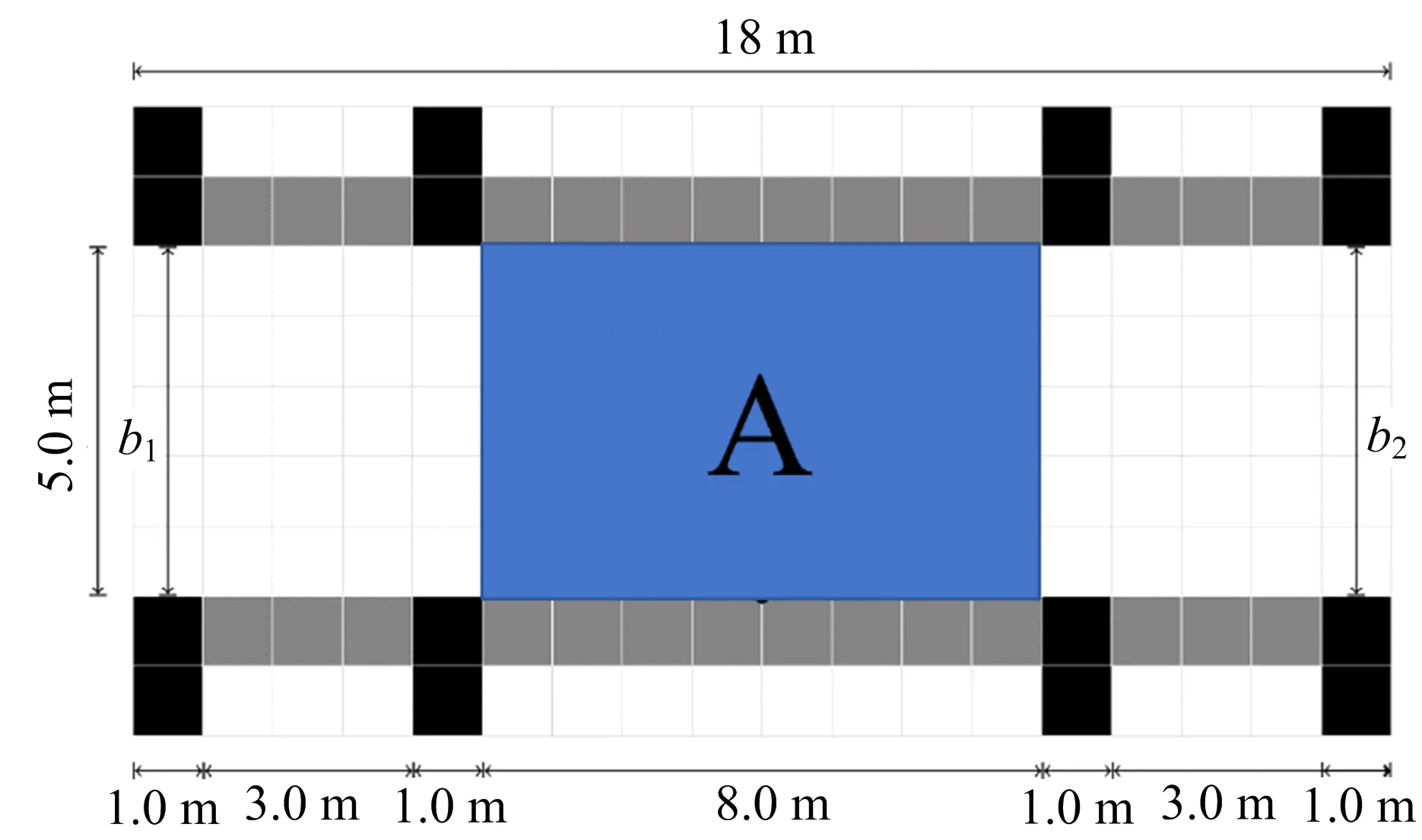
图5 试验场景设置。区域A是我们指定的测量区域。该试验场景宽5 m，长18 m，行人交替从两边进入。Fig. 5 Experiment setup. Area A is our designated area. A five-meter-wide and 18-meter-long corridor was constructed from exhibition walls， Pedestrians are sent alternately from both sides.

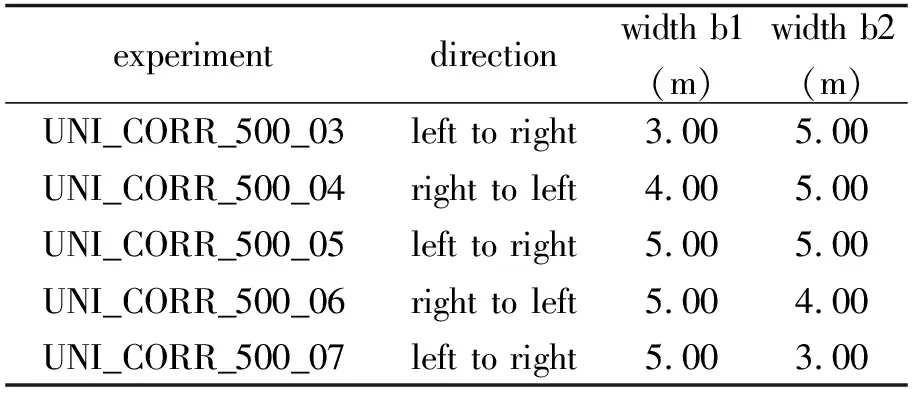
表1 实验设置

为了证明我们的深度基本图网络适用于不同场景，我们选择的实验数据中，03～05组为直通道实验，06和07为瓶颈实验。

在我们的实验中，用平均绝对值误差(MAE)和均方误差(MSE)来评价密度图和速度图估计的准确性和鲁棒性。平均绝对值误差(MAE)表示如下：

(13)

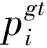
均方误差表示如下：

(14)

MSE越小表示我们的方法鲁棒性越好。

密度图在公开实验上的定量结果和时间-密度关系如表2和图6所示，无论是直通道实验还是瓶颈实验，我们的密度平均误差为0.09，也就是说每平方米相差人数不到0.1人，与真实值相差不大。从基本图来看，通过我们提出的方法得到的基本图与轨迹跟踪方法得到的基本图变化趋势一致，可以描述行人运动整体规律。

表2 行人密度(1/m2)和速度(m/s)的定量结果

图6 (a)，(b)，(c)，(d)，(e)是第3～7组实验中密度随时间的变化图。蓝点线表示轨迹文件得到的地面真值密度，红实线表示CNN得到的密度。Fig. 6 (a), (b), (c), (d), (e) are the time evolution of the density of the third to seventh video. The blue dot line represents the ground truth density obtained from the trajectory file, the red line represents the density obtained from CNN.

速度图在公开实验上的定量结果和时间-速度关系如表2和图7所示。从定量结果来看我们的方法平均误差为0.04，从时间-速度基本图来看，我们的结果更平滑，波动更小，整体趋势与轨迹跟踪法得到的基本图保持一致，可以很好的描述行人运动规律。与密度的MAE相比，速度的MAE值较大，这是由于实验在开始和结束时亮度非恒定，受亮度影响，速度图的鲁棒性波动较大。

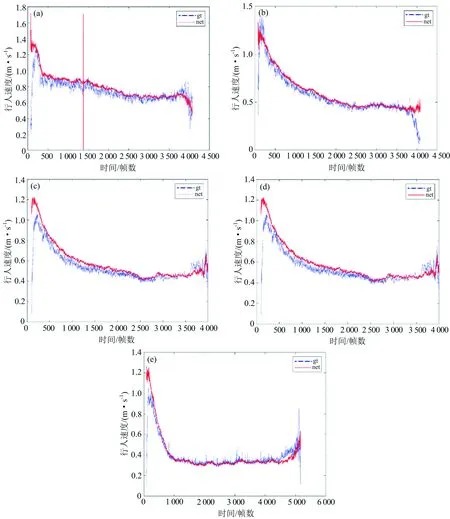
图7 (a)，(b)，(c)，(d)，(e)是第3～7组实验中速度随时间的变化图。蓝点线表示从轨迹文件计算出的行人速度，红实线表示从我们的方法中得到的行人速度。Fig. 7 (a), (b), (c), (d), (e) are the time evolution of the velocity of the third to seventh video. The blue dot line represents the ground truth speed calculated from trajectory file， The red line represents the speed obtained from our method.

表3是获得一帧行人密度和速度所需的时间。因为并行计算，通过MSR-Net获得行人密度所需时间极短。获得一帧行人密度需要进行一次偏差校正，运行时间比获得行人密度的时间稍长，但也不到0.5 s，我们的方法可以直接得到每一帧行人的密度和速度，说明我们的方法可以用于实时获得基本图，对行人动力学实时分析有现实意义。由于我们方法的实时性，在获得基本图的同时可以通过空间对应关系检测出速度和方向异常的行人(如图8所示)，我们的方法对行人动力学分析具有很好的应用前景。

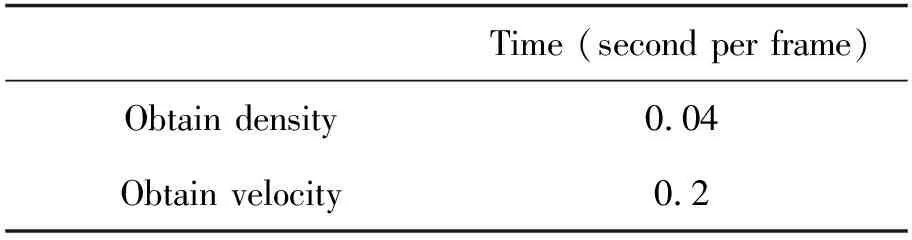
表3 获得行人密度和速度所运行的时间(s)

图8 十二帧连续图像。异常行人(箭头处)用红色标记。Fig. 8 12 consecutive frames. Abnormal pedestrian where the arrows point at is marked in red.

3 结论

本文提出了一种实时获得基本图的方法。利用多尺度递归卷积神经网络对行人密度进行估计，通过光流模块获得行人速度。密度图提供行人密度和行人位置信息，速度图包含行人移动速度和方向。通过密度图和速度图的空间对应关系，我们可以获得基本图。公开数据集的实验表明，我们的方法与轨迹跟踪的方法得到了一致的基本图。我们的方法可以对每一帧图像进行处理并得到这一帧的行人密度和速度，所需的运行时间不足0.5 s，具有实时性。同时，我们的方法可以检测出异常的行人，对行人动力学分析具有很好的应用价值。