某储罐区火灾多米诺效应场景推演

王自龙，蒋 勇

(中国科学技术大学火灾科学国家重点实验室，合肥，230026)

0 引言

随着石油化工产业的快速发展，石油化工企业储罐区规模和储罐容积急剧增长，罐区的大型化提高了化工生产的效率，同时也导致了储罐区火灾事故发生频率和规模的扩大[1]。当化工园区发生事故后，初始事件产生的冲击波、热辐射及爆炸碎片[2]将会导致二次事故的发生，其中，热载荷为重要诱因之一。本文以化工园区储罐火灾场景为例，在考虑热辐射多米诺效应的基础上得到储罐区火灾场景时间空间的演变，为储罐区火灾的应急响应提供依据。

1 储罐区火灾

化工园区特别是储罐区集中分布着大量的易燃易爆物质，一旦由于自然灾害或人为失误发生事故，很容易产生多米诺效应，导致事故扩大[3]。为了对储罐区的火灾事故进行有效扑救，需要对其发生发展的过程进行研究，考虑灾害场景下的多米诺效应。与单个单元的事故场景相比，多米诺效应影响下的储罐区火灾场景通常可以持续更长的时间且拥有更大的破坏区域，因此我们不仅需要关注火灾事故在空间上的发展，还需要对任意时刻的事故场景进行预测。

预测多米诺效应下事故场景随时间的演变并推断多米诺效应下事故的发生序列，对储罐区火灾的扑救和应急资源动态响应需求的预测有着重要的意义。基于连锁效应事故风险评估的必要性，很多学者对连锁事故的风险分析、安全评估和脆弱性分析等进行了系统的研究[4-13]。Cozzani等[4]提出了一种能够识别多米诺效应场景并估计其预期的严重程度的方法，用来处理多米诺效应产生衍生事故的不确定性。随后博弈论[5]，动态贝叶斯网络[6]，事件树等[7,8]方法也被用于化工园区多米诺效应的风险评估中。Khakzad等[9]使用贝叶斯网络来模拟多米诺效应的空间演化，并在潜在的多米诺效应中确定主要事故单元的最可能序列，在贝叶斯网络等复杂推理方法的应用受到限制的事故场景下，又提出了一种基于图论的方法用于化工园区内危险设施的多米诺效应脆弱性分析[10]。Yang等[11]在给定初始事故场景下利用贝叶斯网络不断更新二次事故的发生概率，以此对连锁效应下的事故发展状况进行分析。Zhou和Reniers[12]提出了一种基于矩阵的方法来模拟火灾连锁效应下各单元之间的影响，并通过蒙特卡洛模拟来对火灾事故的传播过程进行分析。Liu等[13]对不确定随机环境中受到退化和冲击影响的设备进行研究，运用随机理论对四种不同冲击模式下设备的可靠性进行了分析。然而，上述的工作大多集中在事故灾害连锁效应的空间演化上,忽略了事故场景随时间的演变，或是获得的事故风险为全局的事故风险对具体的储罐火灾事故缺乏指导意义。为了获取最佳的事故应急响应效果，需要对罐区火灾发生后临近单元火灾事故的动态风险进行研究。

2 储罐区火灾场景构建

以化工园区中某储罐区火灾为研究对象，储罐区的分布情况如图1所示，该储罐区包含四个常压立式内浮顶储罐，其中各个储罐的罐体尺寸和储存体积如表1所示，该地区的年平均温度为20 ℃，年平均风速为3.2 m/s，且风向与T1到T3的方向相同。考虑罐区内储罐均为满充状态且储罐本身防护措施失效的火灾场景，当T1储罐发生浮顶全表面池火后，其临近单元储罐受到T1储罐强烈的热辐射，从而导致储罐设备失效引发二次火灾。当罐区火灾发生时根据当前起火状态对未燃储罐的起火风险进行动态分析，可以得到储罐火灾事故发展的走向，从而判断事故发生后各个时间点储罐区火灾的影响范围。

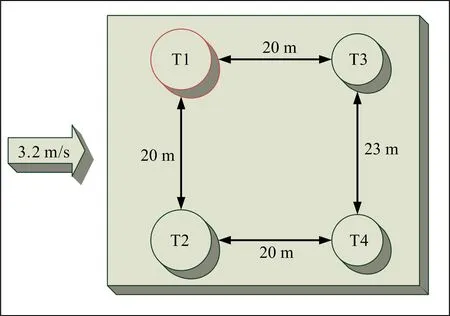
图1 罐区示意图(包含四个常压储罐)Fig. 1 Schematic diagram of the tank area

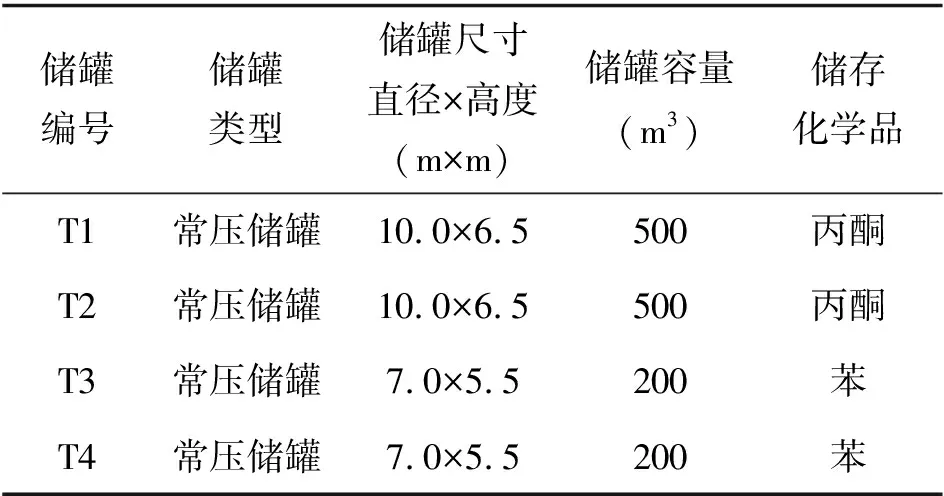
表1 储罐特征描述

当T1发生浮顶全表面火灾后，T1形成的火源持续不断地向其余储罐进行热辐射，虽然其余储罐距离火源T1的距离不同，但是均有着起火的可能性，且当其余储罐中某个储罐起火后，剩余的未燃储罐将会受到所有已燃储罐的共同热辐射作用，增大了未燃储罐在下个时刻的起火概率，从而形成一条由一个单元主要事故引发相邻单元二次事故且规模不断扩大的事故链[14]。

3 火灾场景模拟及事故序列确定

3.1 火灾场景构建

(1)网格划分

本文采用FDS软件对以上储罐区火灾场景进行模拟研究。考虑罐区的实际分布情况和开放空间自由发展火羽流的条件，选取一个60 m×60 m×48 m的长方体作为计算区域，采用0.50 m×0.50 m×0.50 m的均一网格对计算区域进行计算。

(2)探测器布置

由于浮顶全表面火灾主要发生在浮顶和油品的接触部分，因此主要对储罐浮顶处的热辐射通量进行探测。在储罐的浮顶四周设置探测器以探测未燃储罐浮顶所受到的热辐射，并将储罐浮顶四周受到的最大热辐射作为储罐失效的判断依据。

(3)边界条件

由于储罐区火灾在开放的空间内进行，因此将计算区域的四周都设置为开放边界，地面的材料设置为混凝土，储罐壁的材料设置为钢材。

(4)参数设置

根据上节对该储罐区火灾场景的介绍可以对该罐区的环境参数进行设置，环境参数的设置以该地区常见气候为参考。取火灾发生时的环境温度为20 ℃，大气压为101.325 kPa,相对湿度为40%，风速为3.2 m/s，计算时间设置为180 s。

(5)火源设定

本次模拟采用指定热物性参数的方式对罐区火灾的火源进行设定，涉及化学品的热物性参数如表2所示。

表2 化学品热物性参数

其中，燃料的蒸发速率由克劳修斯-克拉贝龙方程进行确定。此时，一旦指定燃料，燃烧就会立即进行，因此模拟过程中燃烧会很快达到稳定，其计算结果仍有着较高的准确性。尽管FDS建模过程中可以写入多种类型的燃料，但在模拟过程中只能有一个气态燃料，为了反映储罐区多储罐发生火灾后对罐区的影响，分别对单一储罐起火场景进行模拟，并对各自的影响进行叠加以得到实际的火灾场景模拟结果。

3.2 网格独立性验证

为了验证计算网格的有效性，增设0.75 m×0.75 m×0.75 m、0.55 m×0.55 m×0.55 m、0.45 m×0.45 m×0.45 m三套网格对T1储罐起火的场景进行模拟，模拟计算时间设置为180 s。T1储罐的热释放速率随时间的变化如图2所示。

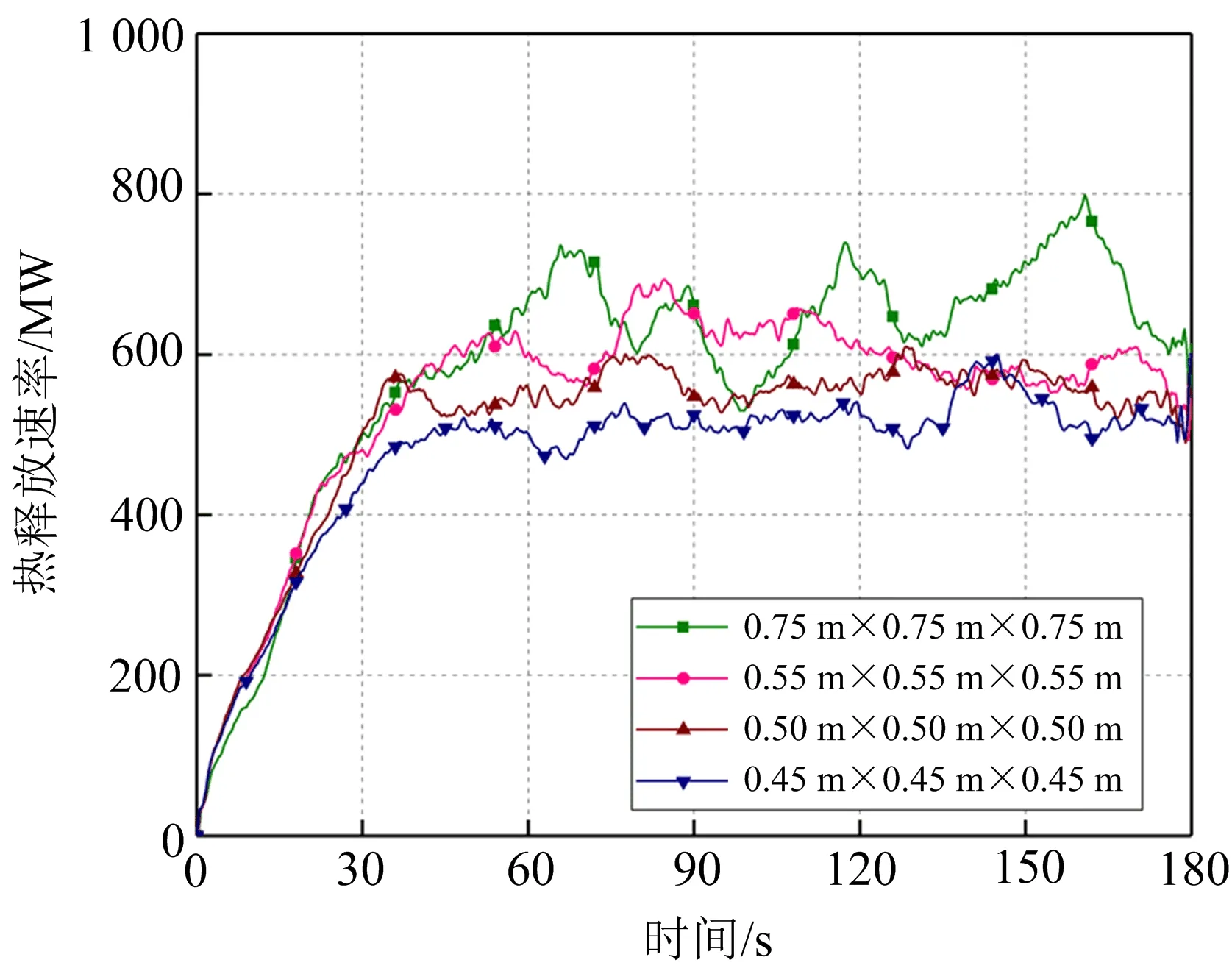
图2 T1储罐的热释放速率Fig. 2 Heat release rate of T1 tank

从图2中可以看出，使用0.75 m×0.75 m×0.75 m的均一网格对计算区域进行划分时，FDS计算得到的T1储罐热释放速率高于其他三类网格且数值波动较大。按照0.55 m×0.55 m×0.55 m、0.50 m×0.50 m×0.50 m、0.45 m×0.45 m×0.45 m均一网格划分的三种工况计算得到T1储罐热释放速率的结果相差不大，从而验证了本次网格划分的合理性。考虑到提高计算效率，降低运算成本的因素，对各个储罐起火状况的模拟采用0.50 m×0.50 m×0.50 m的均一网格划分。

3.3 火灾场景模拟

利用FDS软件分别对罐区内的各个储罐起火场景进行模拟，图3为罐区内单个储罐起火后对其相邻储罐的热辐射强度。可以看出，储罐起火后迅速达到稳定燃烧状态，其对相邻储罐的热辐射强度趋于稳定，储罐所受热辐射强度在时间尺度上的振荡是由火焰结构的波动所致，因此在对起火储罐向相邻储罐的热辐射强度进行研究时，采用储罐池火稳定燃烧后的热辐射强度平均值作为热辐射强度的实际值，如表3所示。

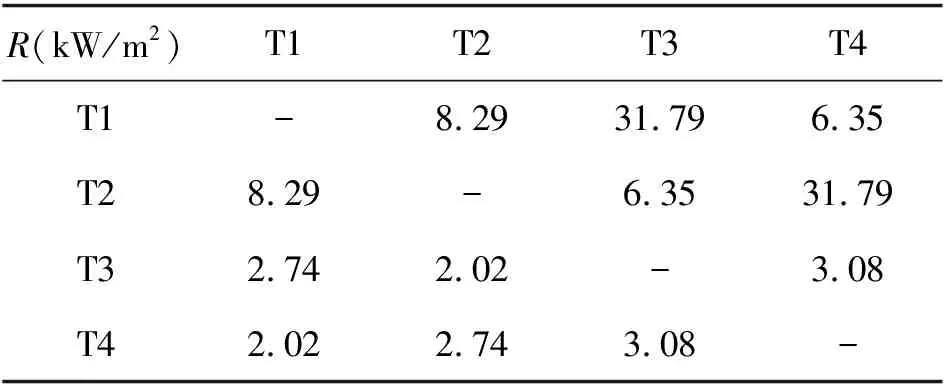
表3 储罐相互之间的热辐射

图3 单个储罐起火后对其相邻储罐的热辐射强度Fig. 3 Thermal radiation intensity of a single tank

3.4 事故序列确定

对该罐区进行事故场景的推演，需要首先对事故发生的序列进行判断。该事故的发展主要依靠储罐之间的热辐射，因此通过引入储罐遭受破坏的热辐射阈值并与事故发展过程中未燃储罐所受到的热辐射量进行比较即可确定四个储罐火灾发生的顺序。

考虑储罐火灾多米诺效应，罐区火灾的发生发展过程中，未燃储罐并非一直受到单一起火储罐的热辐射，以二次事故发生后为例，当初始事故发生之后，初始燃烧的储罐引燃其相邻储罐，这一过程发生后未燃储罐将会受到两个储罐火灾热辐射作用的共同影响。同理，随着事故的不断蔓延发展，未燃储罐将受到所有已燃储罐的热辐射作用，其大小为所有已燃储罐热辐射作用的叠加，称其为联合热辐射。火灾场景下单个或多个热辐射源对未起火储罐的热辐射量如表4所示，其中，“→”表示热辐射传递的方向，数字表示储罐的编号。可以看出当二次事故发生后，未起火的储罐将会受到更强的热辐射，使得之后的事故更容易发生，从而导致事故的规模和影响不断变大。取储罐失效的热辐射阈值[15]为9.5 kW/m2，据表4可以看出当T1储罐起火后，T3所受的热辐射量为31.79 kW/m2，大于储罐热失效的阈值，即储罐T3将会在T1的热辐射影响下起火，在T3起火之前，T2和T4储罐也受到T1储罐火灾的热辐射，分别为8.29 kW/m2与6.35 kW/m2,小于储罐热失效的阈值，因此认为其在T1储罐起火条件下的起火概率为0。当T3储罐发生火灾后，T2和T4储罐将受到T1和T3储罐的共同热辐射分别为10.31 kW/m2与9.43 kW/m2,即T2,T4的未燃阶段，T2所受到的热辐射通量大于T4，因此T2先于T4起火。

表4 多米诺效应下的联合热辐射

由此，该储罐区火灾多米诺效应可以分成四个阶段，各个阶段的热辐射强度分布如图4所示。从热辐射强度场中可以看出在环境风的影响下，储罐浮顶火焰向下风向偏移，导致处于下风向的储罐更容易遭到破坏。当二次事故发生时，当前环境中的热辐射强度急剧增加，周围未燃储罐特别是与起火储罐相邻单位将受到更剧烈的热辐射冲击。

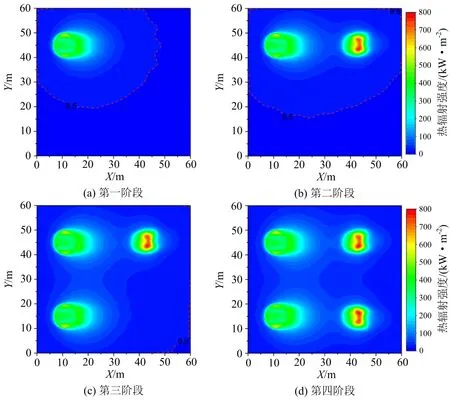
图4 火灾发展各个阶段的热辐射强度Fig.4 Thermal radiation intensity at each stage

为了构建储罐火灾场景随时间的变化关系，选取Cozzani等[4]提出的probit模型进行后续模型的构建。该模型由于其简单性和可操作性被广泛应用于包含各种能量矢量和脆弱性单元的灾害场景。在这里我们主要利用probit模型对热辐射条件下设备失效前时间进行计算，即:

ln(ttf)=-1.13ln(q)-

2.667×10-5V+9.877

(1)

其中，ttf——储罐失效时间，s

q——储罐起火后的热辐射功率，kW/m2

V——储罐容积，m3

根据各储罐之间的热辐射作用可得不同热辐射条件下储罐的设备失效时间如表5所示。

表5 多米诺效应下的设备失效前时间

4 火灾场景推演

为了对储罐状态的变化进行推演，我们将设备失效前时间引入机械失效概率模型中建立起了储罐状态和时间之间的关系，并采用了贝叶斯网络和蒙特卡洛模拟两种方法对多米诺效应下的储罐失效概率进行求解。

4.1 储罐失效概率模型的建立

储罐在热辐射作用下的起火过程可以看作是极端恶劣环境下设备的快速失效，由此储罐失效破坏随时间变化的概率模型[16]可以表达为，

(2)

其中，Pf——储罐起火的概率

ttf——设备失效前时间,min

将表5中各个储罐在不同热辐射条件下的设备失效前时间代入式(2)中即可得到任一热辐射条件下某储罐的着火概率，由此建立起了储罐起火概率随时间的变化关系。

单个储罐起火场景下与其相邻储罐的起火风险可由式(2)求得，然而在考虑火灾连锁效应的情况下未燃储罐所受热辐射强度会由于二次事故的发生而增强，近似为阶梯型的分布，为了对热辐射强度变化时的储罐火灾风险概率进行修正引入了等效热辐射时间t′，并作出如下假设：①不考虑储罐本身的缺陷，灾害场景下的火灾风险仅与其遭受的热辐射总量有关；②由于储罐的对称结构，任一已燃储罐作用在未燃储罐的热辐射面积相同。基于以上假设可得，

(3)

(4)

其中，n——火灾连锁效应的阶段

qn——火灾连锁效应所处阶段的热辐射强度

ttf——热辐射强度突变后的设备失效前时间,min

t′——等效热辐射时间，min

t0——热辐射强度突变的时刻，min

t——火灾持续的时间,min

Pf——储罐起火的概率

由修正的储罐失效概率模型即可得到任意时刻对应热辐射条件下某储罐起火概率与火灾持续时间的变化关系，为下文中储罐火灾风险的动态求解提供依据。

4.2 贝叶斯网络

贝叶斯网络是一种通过有向无环图表示一组随机变量及其条件依赖性的概率图形模型[17]。其中图形的节点表示变量，箭头表示各节点之间的条件依赖性，每个节点的概率与指向其的父节点息息相关。由于贝叶斯网络灵活的结构和强大的概率推理引擎，它被广泛的用于复杂的系统建模和风险分析。

根据以上确定的事故序列以及建立的储罐失效概率模型进行贝叶斯网络参数和网络结构的学习[18]，得到多米诺效应下的储罐失效贝叶斯网络如图5所示，其中，贝叶斯网络中的每个节点表示各个储罐所处的状态，箭头表示各储罐间的概率依赖关系。为了考虑父节点对变量的影响，贝叶斯网络用一组变量的联合分布概率来表示变量的综合概率，如式(5)所示。

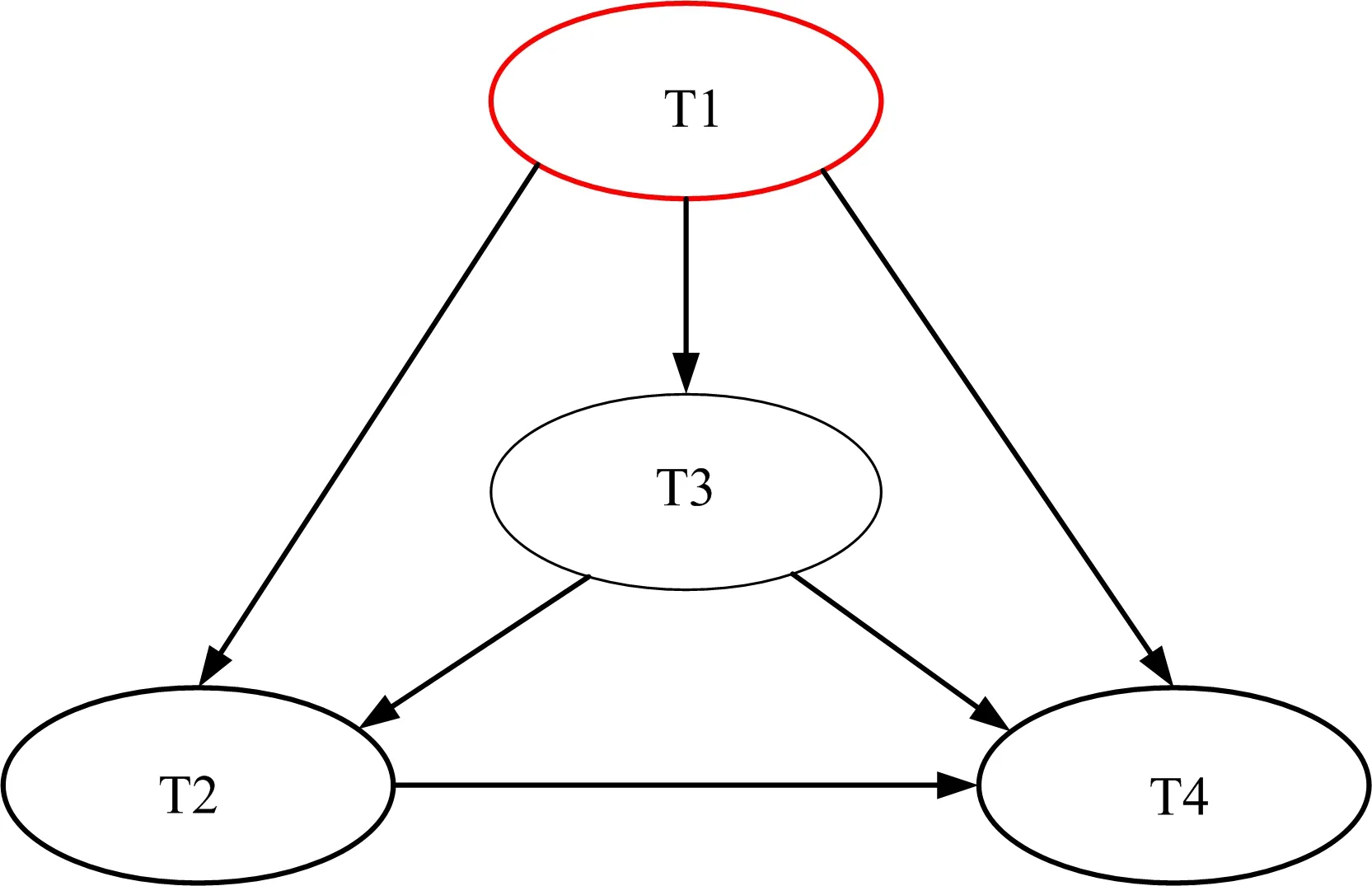
图5 储罐区贝叶斯网络模型Fig. 5 Bayesian network model of tank farm

(5)

其中Pa(Xi)是Xi的父节点，P(U)为变量U的联合分布概率。

这里采用基于MATLAB的贝叶斯网络工具箱BNT对各储罐随时间的失效概率进行计算。根据建立的储罐失效模型可以得到各个储罐的失效概率,如表6～表8所示，其中“S”表示储罐未失效，“F”表示储罐已失效。

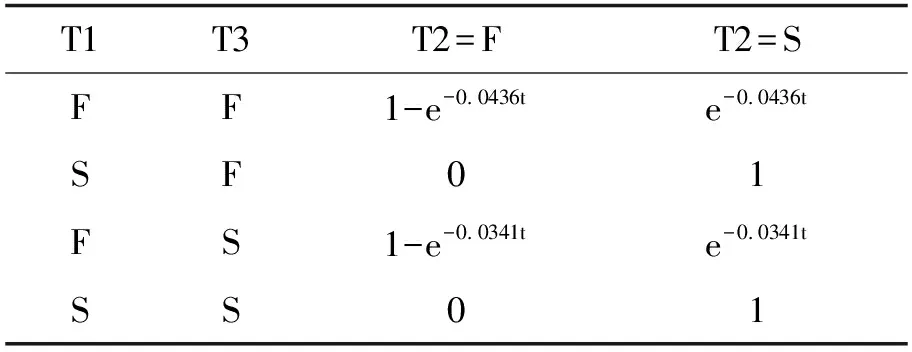
表6 T2失效的条件概率

表7 T3失效的条件概率

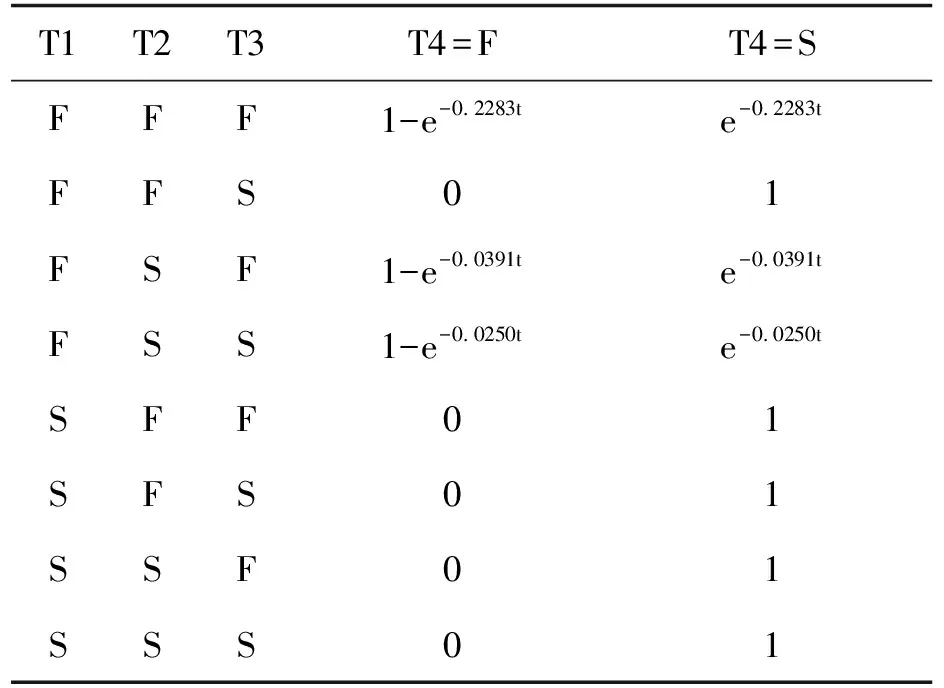
表8 T3的后验失效概率

将每个储罐失效的条件概率导入贝叶斯网络中，并使用联合树引擎对每一个储罐起火的状态概率进行推断，得到罐区内储罐失效概率随时间的变化关系如图6所示。从图6中可以看出，各个储罐的起火风险概率随着时间的发展不断变大，其中受到较强热辐射的T3储罐在火灾发生后火灾风险就急剧上升，而对于距离初始事故距离较远所受热辐射较小的储罐，其火灾风险增长较缓。在不采取任何应急措施的情况下，整个罐区储罐的火灾风险将在初始事故发生的20 min后达到0.6。通过储罐火灾的贝叶斯网络建模，可以快速确定事故过程中的高风险储罐，为事故的断链减灾提供参考。

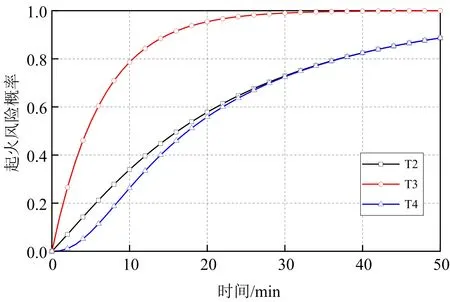
图6 储罐火灾动态风险(贝叶斯网络)Fig. 6 Dynamic risk of tank fire (Bayesian network)

4.3 蒙特卡洛模拟(MCS)

蒙特卡洛模拟(MCS)又被称为统计实验法，它可以通过多次试验求得某个事件发生的频率的方法来求得该事件的发生概率，即在概率模型的基础上按照事件发生的顺序利用数学方法进行模拟实验并以模拟实验的结果作为该事件发生的概率。蒙特卡洛模拟使用随机数集作为输入来实现事件的迭代评估。该方法通常用于高度复杂，非线性或涉及多个不确定参数的系统。当处理事件的潜在概率是已知的但难以确定其相互作用的过程时，蒙特卡洛模拟特别有效[19]。

为了得到每一个储罐的起火风险概率随时间的变化，我们引入蒙特卡洛模拟的方法采用如下步骤进行计算。

step1 输入已知的概率参数；各个火灾发展阶段储罐的修正起火概率(Pij)，蒙特卡洛实验次数(N)，时间步长(Δt)；

step2 初始化事故状态矩阵F和事故状态统计矩阵S，其中未起火状态和起火状态分别用0和1表示；

step3 对输入事故状态进行识别，对未起火储罐的状态进行判断；生成一个0-1的随机数R与未起火储罐当前状态的起火概率Pij进行比较，若R≥Pij直接进入下一个时间步，反之，将装置当前状态置为1(即起火状态)并记录火灾场景发生突变的时间ti用于对下个阶段的储罐风险概率进行修正并进入下一个时间步；

step4 设置判定条件，当目标储罐失效后跳出本次蒙特卡洛实验并进行下一次实验直至所有蒙特卡洛实验完成；

step5 对事故状态矩阵求平均可得储罐起火风险的概率密度分布，进而得到储罐火灾的动态风险概率。

蒙特卡洛实验通过多次模拟火灾事件过程来求得每个时间点罐区起火储罐的数量，以此反映每个储罐在任一时间点的起火概率。图7为106次蒙特卡洛实验得到的各个储罐起火的概率密度分布(FPD)及储罐的动态起火概率(FP)。从图7中可以看出，罐区内各个储罐的状态改变均存在一个时间拐点，在该点之前储罐均处于未燃状态，当储罐火灾的持续时间超过该时间拐点，储罐的状态开始发生改变，由未燃状态变为起火状态。这一现象主要是由于在该时间点前储罐所受热辐射总量较小，没有达到储罐结构遭受破坏的能量阈值，随着热辐射强度的增加，储罐遭受的热辐射强度超过储罐破坏的阈值，导致储罐结构的失效，因此储罐的起火概率在拐点后急剧升高。此外，多米诺效应对储罐的起火概率影响显著，随着二次事故的不断发生，罐区内储罐的起火概率不断增大。尽管根据初始事故判断得到的各储罐失效时间可达20 min以上，然而储罐区的所有储罐仍在20 min达到完全起火的状态，且储罐起火的实际时间要远小于储罐的设备失效时间。因此，在火灾发生时即便储罐还未达到设备失效时间，仍需要对高风险储罐进行重点防护，以防火灾的迅速蔓延。

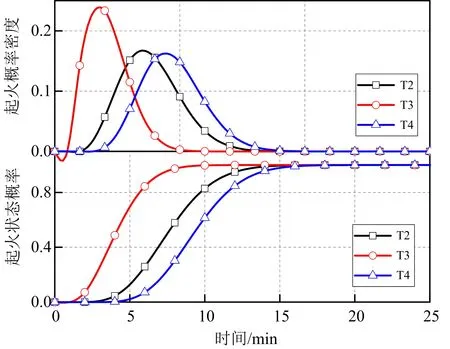
图7 储罐火灾动态风险(蒙特卡洛模拟)Fig. 7 Dynamic risk of tank fire (Monte Carlo Simulation)

5 结论

(1)使用FDS对储罐火灾的事故场景进行构建和模拟，可以获得更为准确的火灾信息，为储罐区火灾事故序列的确定提供依据；

(2)考虑多米诺效应对事故转移和扩大风险的协同效应，并引入恶劣条件下的设备失效概率模型建立储罐失效风险与时间的关系，从而确定储罐火灾发展蔓延过程中的时空演变，为大型储罐区的火灾连锁效应风险评估提供参考;

(3)分别采用动态贝叶斯网络和蒙特卡洛模拟对储罐区储罐的起火风险和起火概率进行了推演，可以为储罐区火灾的应急救援提供更详细的事故场景信息，并为应急资源需求的合理配置提供支持。