盾构竖向姿态的组合预测模型研究

胡长明，侯雅君，李靓，袁一力

(1.西安建筑科技大学 土木工程学院，陕西 西安710055；2.陕西省岩土与地下空间工程重点实验室，陕西 西安710055)

在地铁隧道建设中，盾构法因其机械化程度高、对地面交通影响较小等优点得以广泛应用。盾构姿态控制是盾构法施工的关键控制点之一，一旦盾构机的中心轴线偏离设计轴线，就会造成姿态偏差，进而影响隧道掘进质量。这种偏差会致使盾构机呈“蛇形”运动，对后续的管片衬砌质量的影响较大[1]，同时也会引发土体超挖、地面沉降等问题。目前，姿态控制大多依赖盾构司机的操作经验[2]，主观性较强且多采用事后反馈的方式，只能在产生偏差后采取补救措施，难以及时有效的适应地下复杂施工环境。因此，为提高姿态控制的及时性和有效性，对盾构姿态的预测问题亟待研究。目前，国内外学者针对盾构姿态控制问题展开了大量研究，主要集中于2方面：一是盾构机姿态发生偏移后的纠偏调整。在分析盾构姿态偏移机理后，研究者们通常依据盾构机自身控制器模拟结果[3]、纠偏力矩及纠偏曲线计算结果[4−6]、模糊控制算法协调过程[7]、相关盾构参数分析内容[8]等提出具体的姿态调整措施。然而由于不同地质及施工条件的限制，同时纠偏控制多为对过往偏移规律的归纳及施工经验的总结，事后纠偏难以满足当前盾构姿态控制的及时性需求。二是盾构机掘进前对其姿态进行预测。SUGIMOTO等[9]以满足平衡条件的动力学模型模拟开挖过程的盾构姿态。张爱军[10]建立的BP神经网络模型，可在盾构参数已知的情况下预测上软下硬地层姿态的偏移量。许恒诚[11]在研究了影响盾构姿态的因素间的耦合关系后，建立了基于WT-CNN-LSTM的动态预测模型。孔宪光等[12]通过建立自编码器和深度学习回归模型，对切口水平偏差、切口垂直偏差、盾尾水平偏差、盾尾垂直偏差等盾构姿态参数进行预测。沈翔等[13]基于改进的太沙基松动土压力计算方法，得到了盾构俯仰角理论预测公式。上述研究多采用单一预测模型或是对单一预测模型的改进，只能满足特定条件下的预测需求；并且由于收集的时间序列样本往往并不满足线性条件，上述文献极少考虑初始数据处理对预测结果的影响，难以满足盾构姿态预测的精度要求。鉴于此，本文提出基于粒子群优化的EMD-BP-SVR组合预测方法，以提高盾构竖向姿态时间序列预测的准确性。在利用经验模态分解得到较为平稳的多组序列后，分别对各组序列基于PSO-BP及PSO-SVR模型展开预测，每组序列预测结果叠加即可获得不同模型盾构竖向姿态预测值，最后采用最优加权法对各模型赋权得到最终预测值，从而为盾构姿态预测提供新思路。

1 基本原理

1.1 经验模态分解

经验模态分解算法(Empirical Mode Decompo‐sition,EMD)的基本思想是任何一组时间序列数据都可以分解成有限个具有不同规律及特征尺度的固有模态分量(Intrinsic Mode Function,IMF)和剩余分量。相较原始数据，这些固有模态分量之间互不影响、规律性强且趋于平稳，极大降低了原始数据的非平稳性对预测结果的影响。假设原始时间序列为x(t)，其EMD的分解步骤如下：

1)找出x(t)的极大、极小值；

2)对极大、极小值插值拟合出x(t)的上、下包络线；

3)求得上、下包络线的均值m1(t)，将其从x(t)中剔除，即可获得第1组固有模态分量：

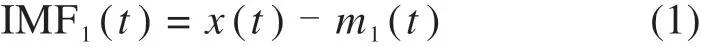
4)从x(t)中剔除固有模态分量IMF1，将剩余分量视为一组新的原始数据，重复步骤(1)～(3)直到剩余分量所成数列符合单调条件或小于设定值，即可获得多组平稳固有模态分量：

式中：IMFi表示第i组固有模态分量；Rn为最终的剩余分量。

1.2 BP神经网络

BP神经网络是一种能学习和训练大量不同样本之间的非线性映射关系的多层次前馈式神经网络。常见的拓扑模型由输入层、隐含层及输出层组成，每层之间通过权值ω和阈值γ建立联系(见图1)。

图1 BP神经网络原理图Fig.1 Schematic diagram of BP neural network

网络训练时，输入信号xi(i=1,2,…,m)，经过隐含层非线性变换得到变量zk，其中k为隐含层个数，可由经验公式计算确定，即：

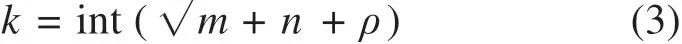
其中，m和n分别为输入层及输出层的个数，ρ为[0,1]之间的常数。信号zk向后传播即可得到输出层信号yj(j=1,2,…,n)。

若末层误差未达期望值，则采用梯度下降法[14]重新分配误差并逐层向前反馈，调整权值及阈值。重复进行上述的信号传播与误差反馈过程，直到获得误差最小的输出信号。

1.3 支持向量回归算法

支持向量回归算法[15]的核心思想是从线性可分的训练样本中划分出一个鲁棒性强的超平面，使得样本中每个个体分布在超平面的两侧(见图2)，定义该平面的模型如下：

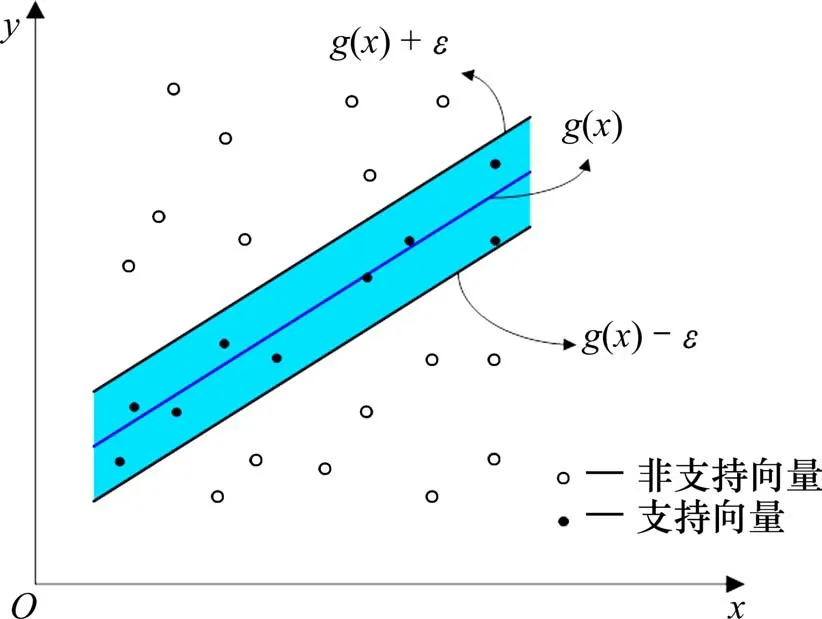
图2 支持向量回归示意图Fig.2 Diagram of support vector regression

其中，λ和b为待确定的模型参数。若预测值g(x)与真实值之间的偏差在[-ε,ε]范围内不计损失，并将g(x)定义为支持向量，否则将计入损失。定义ε-SVR目标函数及损失函数：

式中，C为惩罚因子，表示对超出容许误差的惩罚程度。引入拉格朗日乘子a及a*，将上述问题转为SVR的对偶问题，ε-SVR的解形如式(7)：

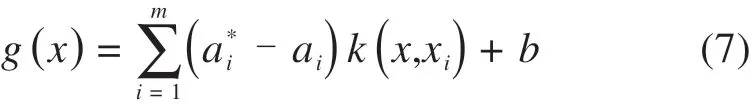
1.4 粒子群优化算法

粒子群优化算法[16]是一种源自鸟群迁徙觅食行为的智能仿生优化算法。粒子在空间中独自寻找个体最优解Ibest，然后依据粒子群内部的信息交互找到全局最优解Gbest，据此调整自身的位置及速度，不断地迭代更新以获得满足条件的最优解。其速度和位置更新公式如下：

其中，p表示当前迭代次数，其取值范围为[1,h]；q表示群体中粒子个数；d表示待优化参数的个数；μ为惯性权重；c1和c2分别为个体及群体的认知能力，r1和r2为[0,1]之间的随机数。本文将BP神经网络的权值(ω)、阈值(γ)与SVR的惩罚因子(C)、核函数参数(g)作为待优化参数。

2 组合模型

盾构掘进过程中需要实时监测盾构机的位姿参数，以刀盘前端中心为原点建立三维坐标系，位姿参数通常包括俯仰角、横摆角及扭转角等。经分析收集数据，本文以俯仰角为研究对象，即盾构机轴线与水平面所成夹角，向上为正，向下为负(见图3～4)。

图3 千斤顶分布Fig.3 Jack distribution

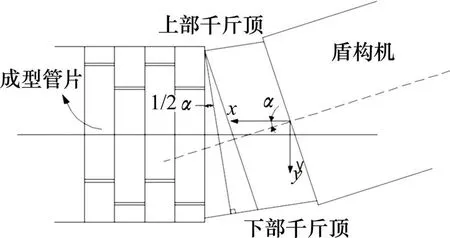
图4 俯仰角示意图Fig.4 Schematic diagram of pitch angle

由于俯仰角时间序列波动性强，仅用单一模型会导致预测性能不佳，因此本文采用BP-SVR组合预测方法来提高单一模型预测的性能，并将组合模型定义为：

式中：Yt为第t个测试样本的最终预测结果，Yt1，Yt2分别为PSO-BP和PSO-SVR模型第t个测试样本的预测结果，η为PSO-BP预测值占最终预测结果的比重。本文利用最优加权法[17]求解η值，该方法以调和平均误差平方和最小为目标，以期获得最优权值。设俯仰角时间序列为{x(t),t=1,2,…,n}，故其加权调和平均预测值为：

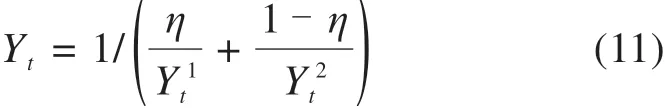
考虑到最优加权法的基本思想，式(10)可转化为求解最优问题模型：

针对式(12)，基于MATLAB 2018b求得最优解，以此得到满足训练与预测要求的组合模型，具体实现步骤见图5。

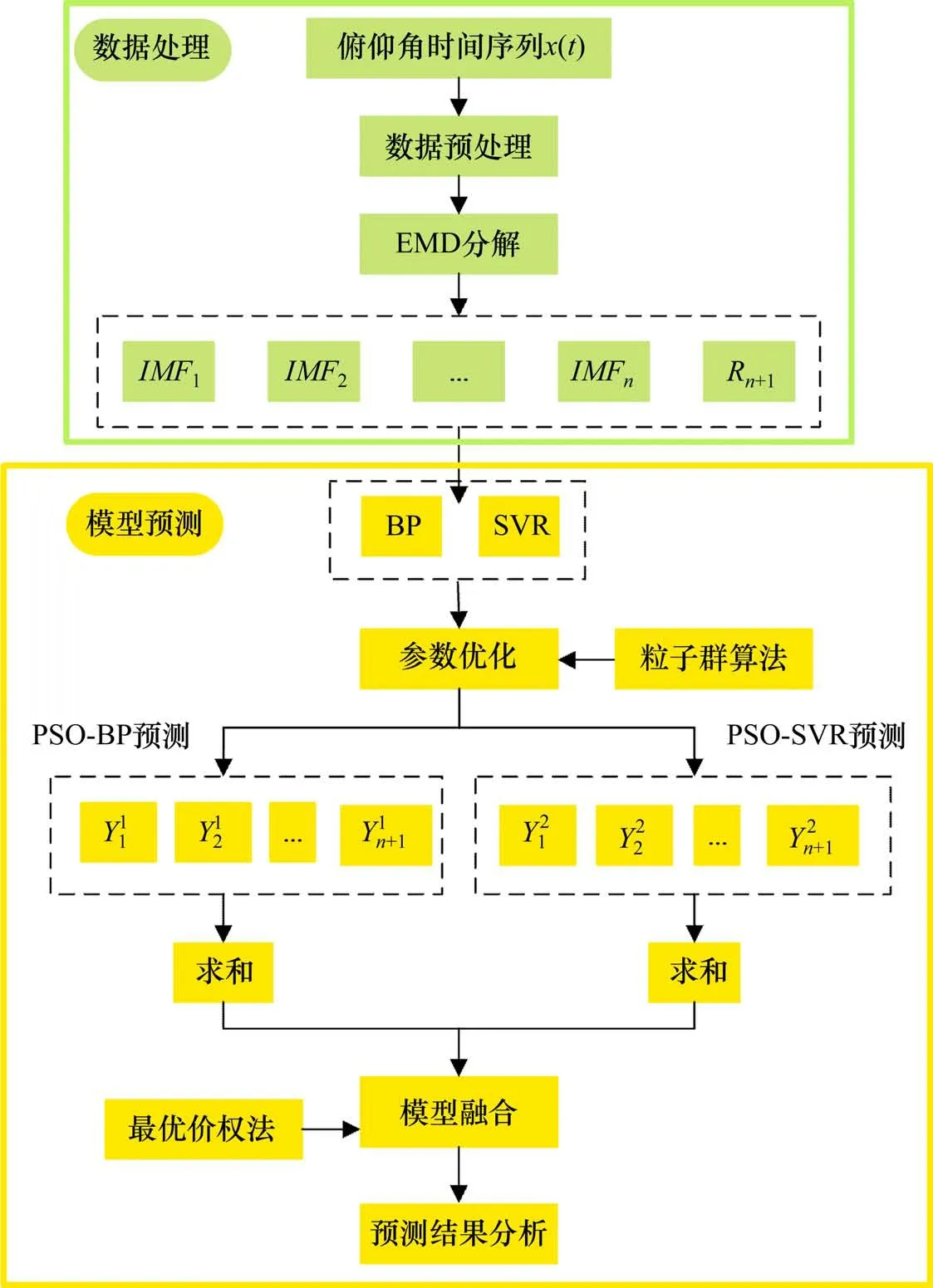
图5 盾构竖向姿态预测流程图Fig.5 Flow chart of shield vertical attitude prediction

3 工程应用

3.1 工程背景

本文依托成都地铁8号线某标段，该标段地处成都平原、地势平坦开阔，穿越岷江水系、地下水流丰富，下穿复合地层、环境复杂多变。目前河流、地下水等基本已受到人为的改造和控制，地铁隧道施工受水流影响较小。地铁掘进路线属典型的卵石泥岩复合地层，隧道围岩各层特性见表1；上层卵石会给围护桩、导管以及盾构施工带来困难和风险，其高渗性也会给工程降水和注浆带来困难；隧道围岩揭露的泥岩属易风化岩，泥岩层强风化呈半岩半土、碎块状，软硬不均，软弱夹层较发育，在水的影响下易发生胀缩破坏。盾构机在该标段掘进过程中需建立严格的监测控制系统，定期进行监测，确保隧道盾构结构和周围环境的安全。

表1 各土层属性Table 1 Property of ground layers

3.2 模型训练

3.2.1 数据选取与处理

本文的输入及输出变量均为盾构机的俯仰角，每个样本点采集数据均为盾构机向前掘进一环后的俯仰角，依据上述原则从所在标段中选取相邻220环的俯仰角作为原始数据。利用分箱法筛选样本中的离散数据，将其剔除后，与缺失值一并按照邻近数据的线性关系补齐。补齐后，对样本数据进行EMD分解，得到6组固有模态分量(IMF1～IMF6)和1组剩余分量Rn，具体如图7所示。

同时，为提高模型收敛速度，对数据进行归一化处理，公式如下：

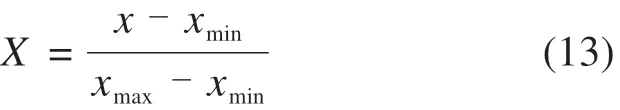
其中，X为归一化后的数据，x为原始数据，xmin，xmax分别为原始时间序列的最小值及最大值。

本文的预测问题属于时间序列问题，预测时采取滚动式方法，滚动步长为10，滚动步距为1，即以1～10环的数据预测11环的俯仰角，以2～11环的数据预测12环的俯仰角，依次类推，每个分量均可获得210组输入变量(X1～X10)及输出变量Y。本文随机选取其中200组为训练样本，剩余10组为测试样本。

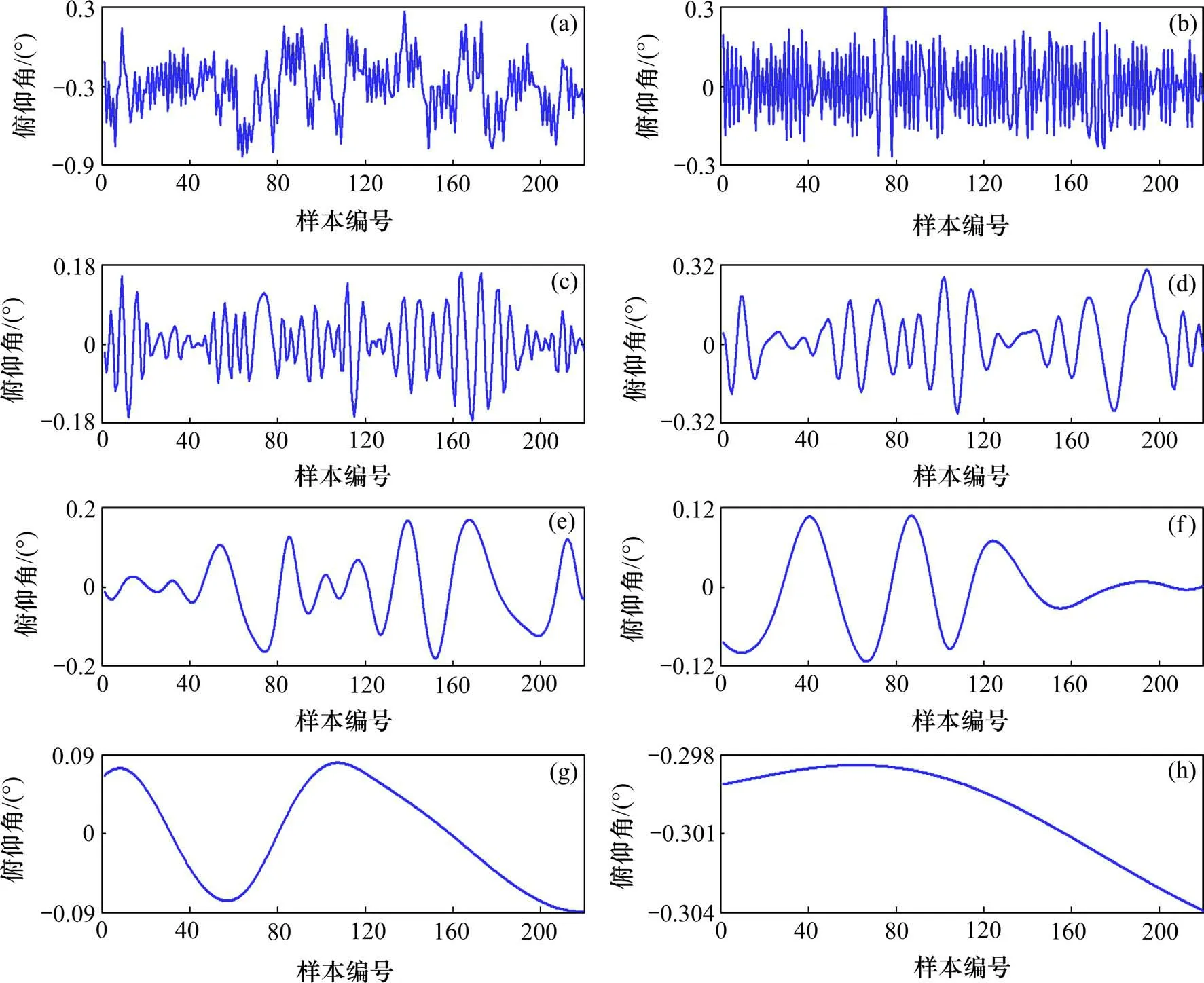
图6 俯仰角时间序列EMD分解结果Fig.6 EMD decomposition results of pitch angle time series

3.2.2 模型融合

1)PSO-BP模型由于本文将前10个样本点的俯仰角为输入值，当前样本点的俯仰角度为输出值，以此可以确定BP及PSO算法所用初始参数(见表2)。同时由表2易得，该模型每次预测时待优化的参数共有(10+1)*13+(13+1)*1=157个。训练时隐含层的激励函数选取sigmoid函数，输出层的激励函数选取logsig函数，整个BP神经网络的训练则需调用MATLAB软件自带的trainlm函数。将各个分量的200组训练样本分别输入软件中学习训练神经网络，以输出变量误差的二范数为粒子群算法训练目标，迭代寻找全局最小误差二范数，记录当前的权值及阈值并将其赋给新的神经网络，训练后便可得该分量俯仰角预测值，求和即得PSOBP模型预测值。

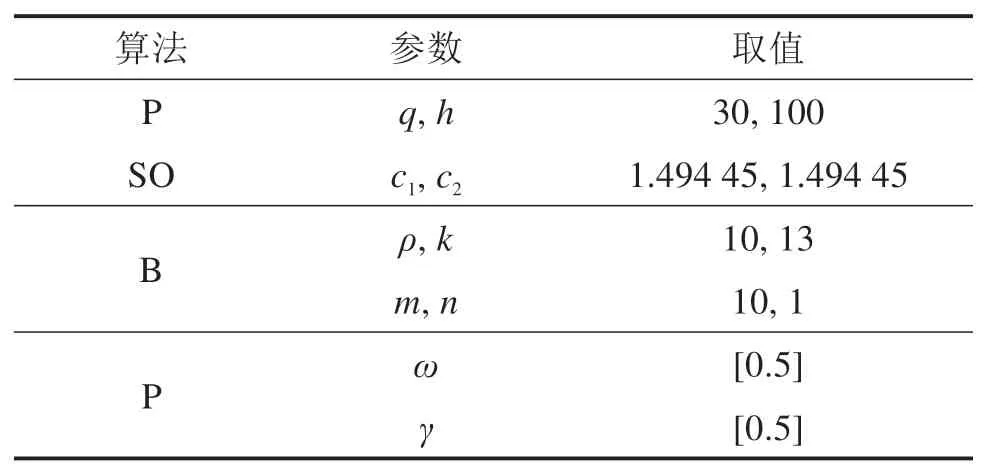
表2 PSO-BP模型初始参数设置Table 2 Initial parameter setting of PSO-BP model

2)PSO-SVR模型PSO-SVR模型内部参数初始设置如表3所示，以均方误差(MSE)为PSO算法的训练目标，旨在寻求各个分量的最佳惩罚系数与核函数参数，以此进行盾构竖向姿态SVR模型仿真测试，该模型的最终预测结果为各分量预测值之和。

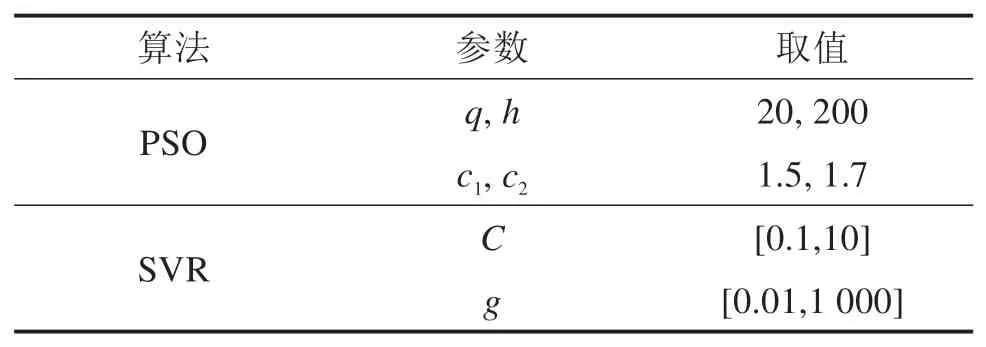
表3 PSO-SVR模型初始参数设置Table 3 Initial parameter setting of PSO-SVR model

3)预测结果为更直观地分析预测结果，在计算调和误差et的基础上分别计算单一模型及组合模型的均方误差(MSE)、平均相对误差(ARE)、平均绝对误差(AAE)、最大相对误差(MAE)及相关系数(R2)，并对上述指标做归一化处理，具体见下：

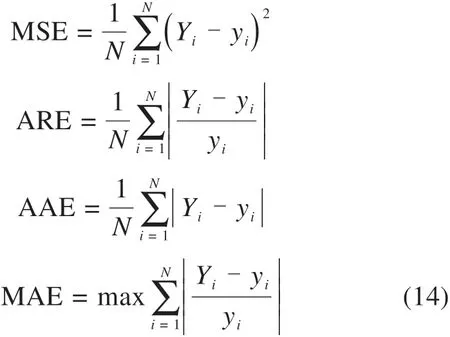
其中，Yi为模型预测值，yi为原始数据，N为预测样本的个数。相关系数则反映预测值与实际值之间的相关程度，相关系数越大说明二者相关程度越高；各类误差反映了预测结果的离散程度，误差值越小表明预测越准确。

将各分量样本数据分别代入PSO-BP与PSOSVR模型，在获取盾构俯仰角的预测值后，基于式(11)～(12)所述最优加权法定权即得最佳预测结果，各个模型的预测结果对比如图7所示。经MATLAB寻优发现，当η取0.328时，调和平均误差平方和最小，故最终的组合模型为Yt=0.328Yt1+0.672Yt2。与原始数据相比，单一模型预测值波动较大，难以保证预测的准确性；本文方法获得的寻优结果则波动较小，拟合效果更佳。

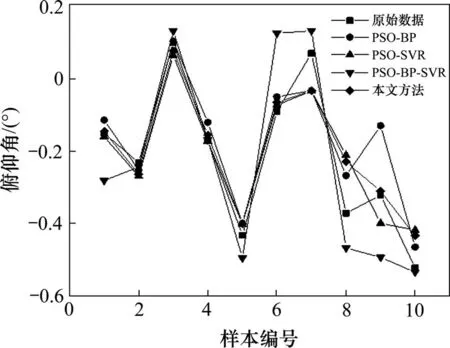
图7 测试集预测结果与实测数据对比Fig.7 Comparison between test set prediction results and actual measured data

表4 和图8均为各模型各类误差指标及相关系数的对比，其中PSO-BP-SVR模型表示未经EMD分解的组合模型，且图8数据为经归一化处理的数据。显而易见，单一BP和SVR模型各类误差值都较高，相关系数分别为93.15%，92.96%，未经EMD分解的模型误差值更大，各有不足。相较之下，本文采用方法相关系数有所提高，均方误差、平均相对误差、平均绝对误差大幅降低。总体上，本文所建组合模型预测精度明显有所提高、在降低误差方面有着较好的表现。

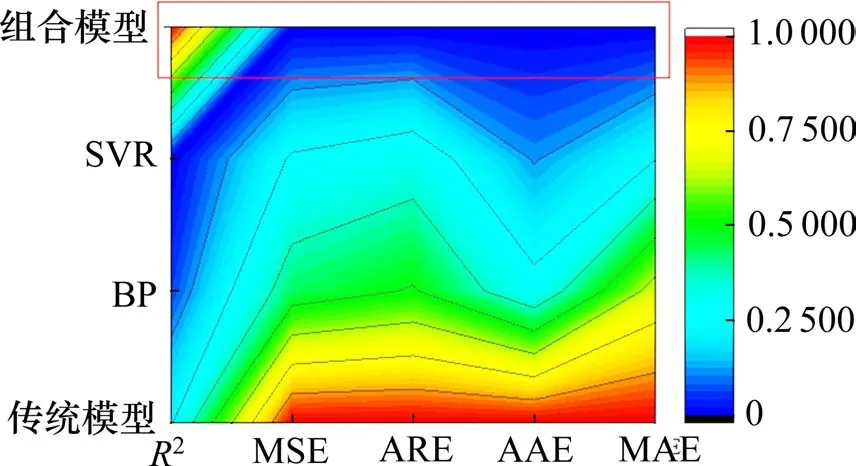
图8 各模型误差对比(归一化后)Fig.8 Error comparison of each model(after normalization)

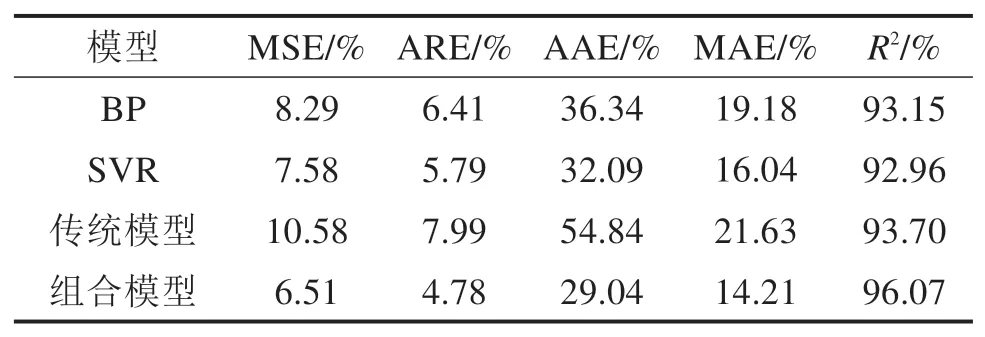
表4 各模型误差对比Table 4 Error comparison of each model

4 结论

1)采用EMD法对盾构俯仰角时间序列进行预处理，将复杂的原始时间序列分解为较为简单的信号，为处理非线性预测问题提供了思路。根据滚动法建立的俯仰角预测数据集，在充实样本数据的同时提高了模型性能。

2)对比单一模型与BP神经网络和SVR的加权组合模型预测结果，可以发现：组合模型的MSE，ARE，AAE和MAE明显低于单一预测模型，R2达96.07%，说明组合模型可有效地将2类模型的优点相融合。对数据进行经验模态分解处理后，剔除了数据中的大量随机因素，此时俯仰角时间序列趋于平稳，预测精度大幅提高。可见本文所建组合模型在非平稳、非线性、小样本的盾构姿态预测问题。

3)基于成都地铁8号线进行拟合分析，得到的预测值与实际值高度吻合，验证了本文所建模型的可靠性，可为日后盾构竖向姿态预测问题提供参考。