移动展开式跨越架的设计与优化

罗 杰, 罗义华, 李 亮, 张金锋, 周焕林

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.国网安徽省电力有限公司,安徽 合肥 230022)

随着经济的发展,电网建设速度日益加快,架空输电线路跨越公路、铁路、已有输电线路等设施的情况很多。在新建的输电线路架线施工时,需要在这些设施上方搭设跨越架,保障被跨越的设施正常运行,同时保障放线施工的安全。传统跨越架有脚手架式、抱杆式等,需耗费大量的人力、物力,且机械化程度较低,难以满足现阶段施工要求。针对传统跨越架的缺点,急需研制出一种快速机动、安全性高的新型跨越架。

文献[1]介绍了一种可重复使用的抱杆自立式跨越架;文献[2]介绍了一种新型输电线路自升降式跨越架,该跨越架可根据实际工况调节高度,具有较高的实用性。在文献[2]理论的基础上,本文设计了一种新型移动展开式跨越架。该跨越架安装在载重汽车上,可液压顶升展开,可快速就位、展开、收回和撤离。

跨越架主要承受自重、风荷载和导线荷载的作用，跨越架的设计可参考类似的起重机械、仓储货架等钢桁结构的优化方法。

文献[3]开发了一种具有优化设计功能的软件,为平头起重机臂架的设计与优化提供了借鉴;文献[4]利用有限元软件对动臂式起重机起重臂进行了静力学分析;文献[5]提出了一种改进的萤火虫算法,并利用该算法对杆系结构拓扑优化,证明其可行性与高效性;文献[6]利用萤火虫优化算法对桥式起重机的主梁截面尺寸进行了优化,使其质量在保证安全的前提下达到最轻;文献[7]提出一种基于萤火虫算法的仓储货位优化方法,解决了仓储系统货位的优化问题。

本文针对传统跨越架的不足,提出一种移动展开式跨越架结构,并结合萤火虫算法和有限元分析,对其进行优化设计。

1 移动展开式跨越架设计

1.1 跨越架基本情况

本文设计的移动展开式跨越架最大工作高度为13 m,架立后最大跨越宽度可达11 m,臂架上顶面可形成宽6 m的放线平台,无需其他封网装置。架体主要由主杆和臂架2个部分构成,长度均为11 m。主杆与运输车及臂架间均采用双臂液压顶伸装置,可实现架体的架设与收回。转动结构具有灵活机动、收缩后尺寸小、不占空间的特点。主杆横梁和臂架中间横梁长度均为2.50 m,臂架两侧横梁长度为1.75 m,对坠落导线起支撑作用。

该新型跨越架结构示意图如图1所示。

图1 新型跨越架结构示意图

快速机动跨越架跨越施工主要分为以下几个步骤:

(1) 在被跨越物两侧定位运输车的准确位置,然后进行液压顶升工作。

(2) 利用上液压柱将臂架顶升至与主杆呈15°角,以防止臂架端部触及车辆驾驶室。

(3) 利用下液压柱将架体顶升至与车体上表面垂直,再利用上液压柱将臂架顶升至水平状态,从而实现跨越架架体的快速搭建。

(4) 释放铰接于臂架端部的支撑杆,并将其底部固定在地面上,由此在障碍物上形成架线通道。

1.2 荷载工况

根据跨越架在实际工作中的受力情况,该跨越架承受的主要荷载有风荷载、自重以及在工作工况下的导线荷载。其中,风荷载分为正常工作风荷载(风速15.5 m/s)和极限大风荷载(风速28.3 m/s)。按每一个高度区段为10 m,换算成节点荷载均分到该区段跨越架结构上。根据《起重机设计规范》[8],风荷载的计算公式为:

(1)

pw=CpAsin2θ

(2)

其中:p为计算风压;vs为计算风速;pw为作用在构件上的风荷载;C为风力系数;A为构件垂直于风向的实体迎风面积;θ为风向与构件纵轴或构件表面的夹角(θ<90°)。

参考《建筑结构荷载规范》[9],新型跨越架所承受的荷载组合见表1所列。

表1 荷载工况

1.3 有限元选型

根据该跨越架的荷载工况,利用有限元软件进行对比分析,得到跨越架结构主要构件的截面尺寸(单位为mm)、壁厚等信息见表2所列。

表2 跨越架结构主要构件信息

2 有限元分析

2.1 有限元模型

对设计的新型跨越架进行适当简化,建立有限元模型如图2所示。

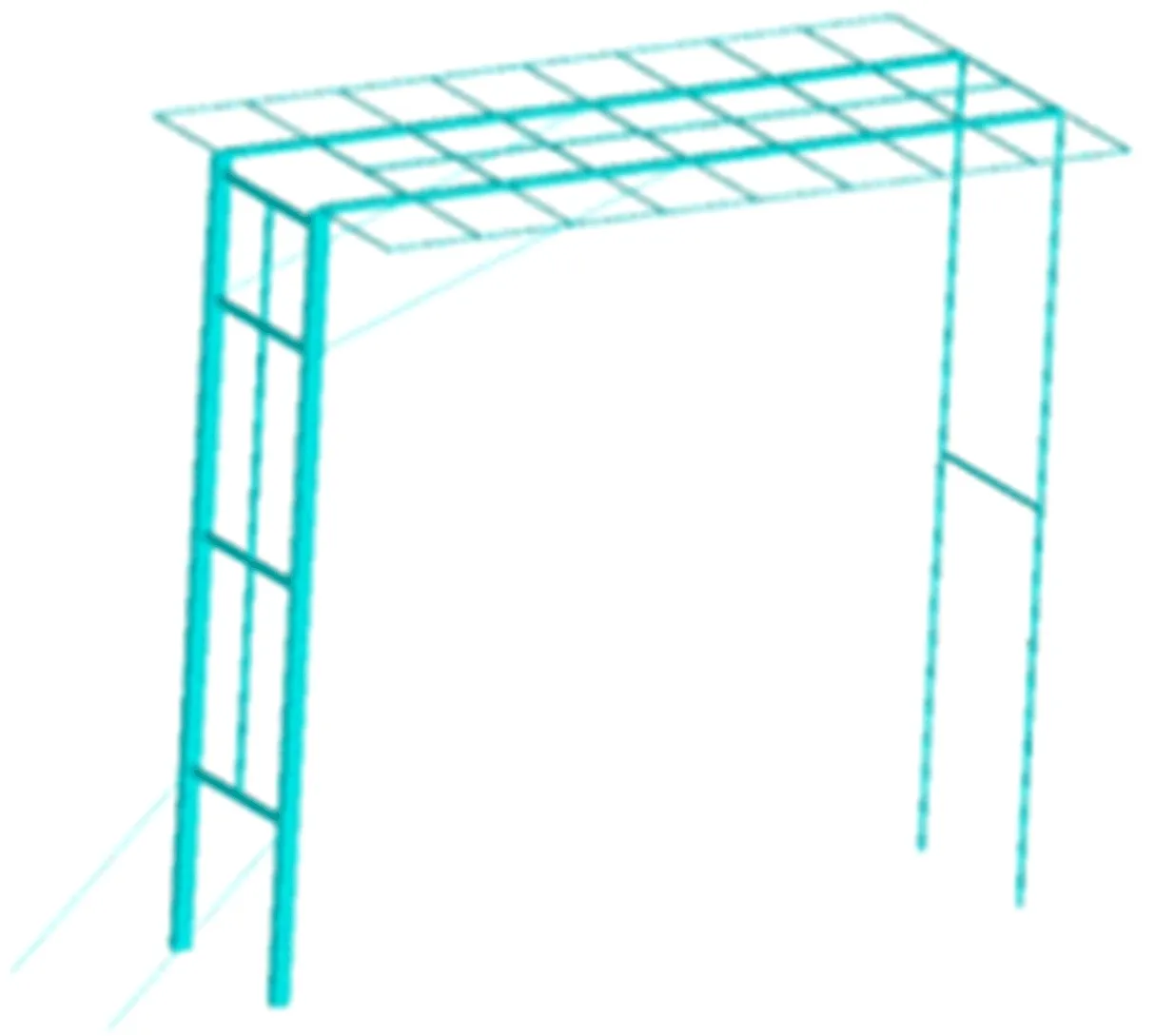
图2 新型跨越架有限元模型

采用BEAM188单元模拟主杆、臂架、撑杆,采用LINK11单元模拟双臂液压柱。通过释放自由度来实现转台与主杆、主杆与臂架、臂架与支撑杆之间的转动连接,支撑杆下端固接于大地,其他主要承载构件连接处均设定为刚性连接。

2.2 应力分析

采用ANSYS软件求解9种工况下新型跨越架的应力结果。该新型跨越架在各工况下的最大Mises应力计算结果如图3所示。将该结果与《钢结构设计规范》[10]规定的屈服强度进行对比分析。

由图3可以看出,工况8时最大Mises应力为119.35 MPa,出现在撑杆中部横杆处。这是由于在该工况下臂架受沿着Z轴正向作用的大风荷载时将出现扭转,使得支撑杆的横杆受力较大。材料的许用应力为156 MPa,该最大应力值未超出材料的设计值,满足强度要求。

图3 各工况下的最大Mises应力

2.3 位移分析

求解各工况下新型跨越架的最大位移。安装、工作、大风工况下的最大位移见表3所列，9种工况下的最大位移如图4所示。

表3 安装、工作、大风工况下的最大位移 单位:mm

图4 9种工况下最大位移

由图4可知,9种工况下臂架和支撑杆位移变化量较大,且最大位移位置一般在臂架端部或中部。

工况8下该新型跨越架结构位移云图如图5所示。

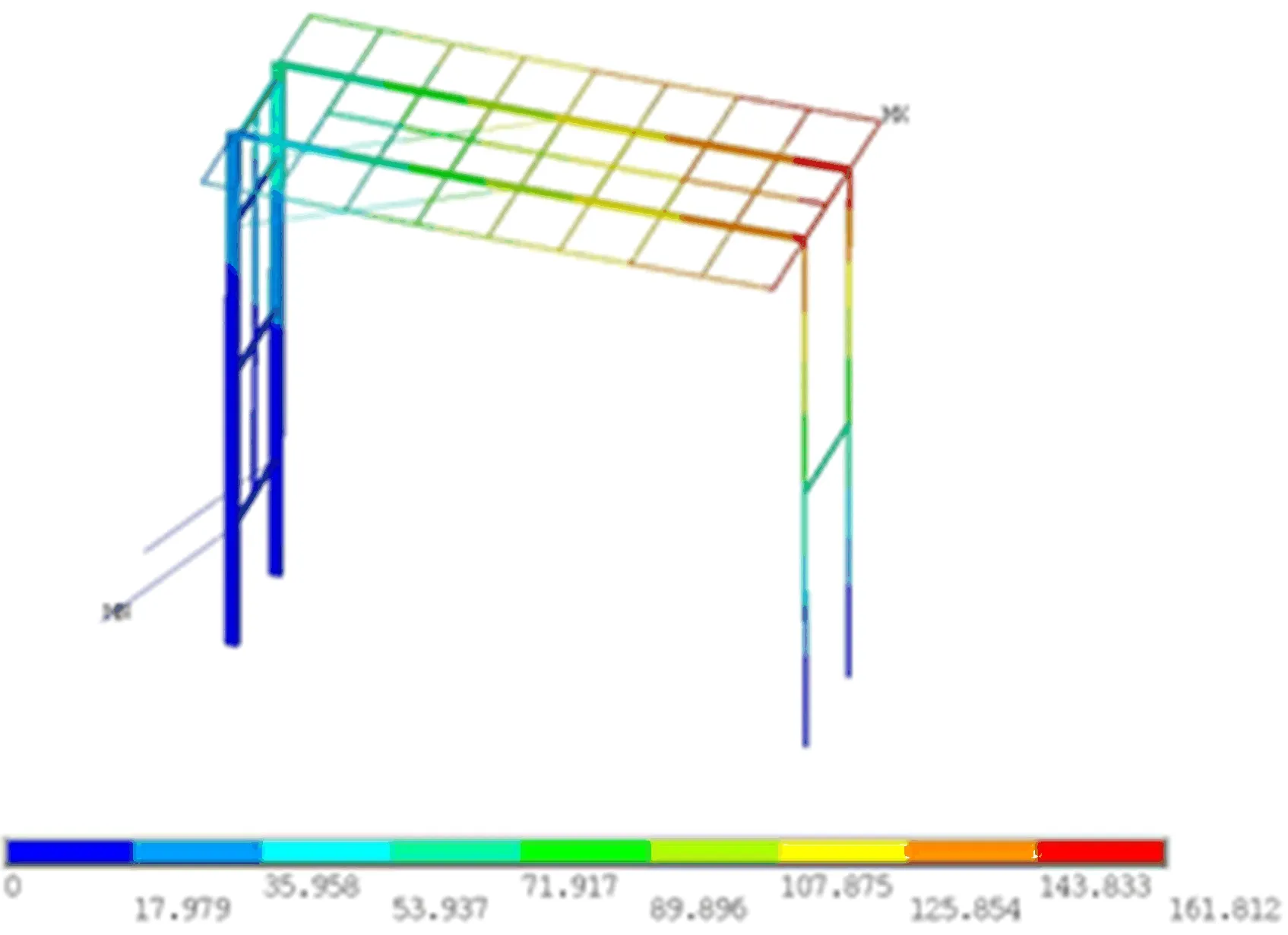
图5 工况8下结构的位移云图

从图5可以看出，在工况8下,结构达到各工况下最大位移161.81 mm,这是由于臂架受大风和最不利风向的影响,从而出现位移偏大的情况。当跨越架顺着风向放置时(工况7),此时最大位移值为103.98 mm,各节点处的位移相比于工况8时减小很多。

因此，大风时可将跨越架架体旋转至顺风向以提高其安全性。

3 新型跨越架结构优化设计

3.1 优化模型

在有限元选型的基础上,利用萤火虫算法对跨越架截面尺寸进一步优化。以新型跨越架结构的结构强度和刚度为约束条件,跨越架的截面尺寸和壁厚为设计变量,臂架结构质量最小化为目标建立优化模型。

根据跨越架结构的特点,选取主杆中竖杆截面的宽度与高度(L0、W0)、臂架主梁截面的宽度与高度(L1、W1)、主杆竖杆壁厚T1、臂架主梁沿宽度方向壁厚T2、臂架主梁沿高度方向壁厚T3、主杆横梁壁厚T4以及臂架横梁壁厚T59个变量作为设计变量,参考各构件原始尺寸确定变量区间。

设计变量记为:

x=[L0W0L1W1

T1T2T3T4T5]

(3)

将跨越架结构质量W(x)作为优化设计的目标函数,即

F(x)=minW(x)

(4)

应力变量σ和位移变量δ为2个状态变量,对应的约束条件为:

σmax≤[σ]

(5)

δmax≤[δ]

(6)

其中:σmax为跨越架结构的最大Mises应力;[σ]为材料的许用应力;δmax为跨越架结构的最大位移;[δ]为结构的许用挠度。

3.2 优化方法

3.2.1 萤火虫算法

萤火虫算法是一种源于对萤火虫群体行为简化和模拟的高级启发式算法,属于群智能优化算法[11-12]。相比于其他智能优化算法,萤火虫算法的优点在于步骤清晰明确、迭代参数较少、操作简单方便。

标准萤火虫算法的基本流程为:① 首先进行算法初始化；② 通过不断迭代更新萤火虫位置；③ 在达到指定迭代步数或求出满足要求的优化目标值时终止计算。

(1) 萤火虫没有雌雄之分,任何一只萤火虫都会吸引其他所有萤火虫。

(2) 萤火虫的吸引力与它们的亮度成正比。亮度大的萤火虫会吸引亮度小的萤火虫向其不断靠近,而亮度大的萤火虫则随机移动。这种吸引力会随着萤火虫间距离的增大而减小。

(3) 萤火虫的亮度是由待优化的目标函数决定的。

萤火虫算法的核心思想是绝对亮度小的萤火虫会被绝对亮度大的萤火虫吸引,并根据位置更新公式来更新自身所处的位置。萤火虫的绝对亮度是指某只萤火虫的初始光强度,相对亮度是指某只萤火虫在其他萤火虫所在位置处的光强度。吸引力大小是由萤火虫之间的相对亮度决定的。考虑到萤火虫的亮度随着距离的增加以及空气的吸收而减弱,则定义萤火虫之间的相对亮度为:

(7)

其中：Ii为萤火虫的绝对亮度,等于所处位置的目标函数值,目标函数值越优,绝对亮度越大;γ为光吸收系数,一般取常数;rij为萤火虫i与萤火虫j之间的距离。

萤火虫i对萤火虫j的吸引力βij(rij)为:

(8)

其中,β0为最大吸引力,即在光源处(r=0处)萤火虫的吸引力。

由于被萤火虫j吸引,萤火虫i向其移动来更新自身的位置,i位置更新公式如下:

(9)

(10)

其中：rij为萤火虫i到萤火虫j的笛卡儿距离,可由(10)式进行计算;xi、xj为萤火虫i和j所在的空间位置;t为萤火虫算法的迭代次数;α为步长因子,一般可取α∈[0,1];εi为随机数向量。显然,位置更新公式中的第2项是由萤火虫之间的吸引力来决定的,第3项则为包含特定系数的随机项。

式(24)虽然消除了辅助参数但θ2中却同时引入了另外的辅助参数ρ.显然，θ2中ρ和x,y是相关的，因此式(24)的结果同样并非最优.为此，在第3步中，利用θ2中辅助参数ρ与目标位置x,y的约束关系来构建方程，从而进一步提高目标位置的估计精度.考虑的估计误差，则由ρ=x2+y2可得：

3.2.2 罚函数法

罚函数法是用来解决约束优化问题的一类方法,其基本思想是将约束优化问题转变为无约束优化问题来求解。罚函数是由目标函数和约束函数进行某种组合而得到的函数。对于等式约束的优化问题，即

(11)

可定义如下罚函数:

(12)

对于不等式约束的优化问题,即

(13)

可定义如下罚函数:

(14)

其中,C为罚函数参数(罚因子),表示惩罚力度的大小。

若优化问题中同时存在等式约束和不等式约束,则组合上面的2个罚函数。

3.3 优化结果

优化过程中目标函数的变化曲线如图6所示。

图6 目标函数值变化曲线

对计算结果进行分析,得到各设计变量优化前与优化后的数值和变化率,见表4所列。

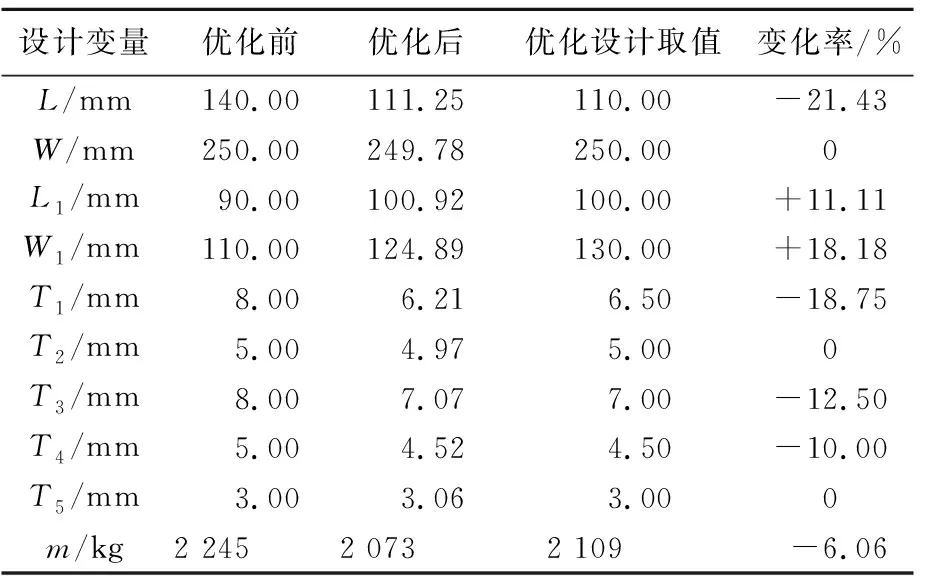
表4 设计变量优化前与优化后的数值和变化率

由表4可知,优化后该新型跨越架结构主杆中竖杆截面的宽度L0、主杆竖杆壁厚T1、臂架主梁沿高度方向壁厚T3、主杆横梁壁厚T4均有较大幅度的减小,臂架主梁截面的宽度与高度(L1、W1)有所增加,主杆中竖杆截面的高度W0、臂架主梁沿宽度方向壁厚T2、臂架横梁壁厚T5基本保持不变。

参考《热轧钢板和钢带的尺寸、外形、重量及允许偏差》[13]对公称尺寸选取的要求,选取优化设计值同表4。优化后该新型跨越架的质量由2 245 kg减小到2 109 kg,降幅达到6.06%,优化效果明显。

3.4 结果验证

按照优化设计选取的变量尺寸修改模型,并进行有限元静力计算分析,优化前和优化后9种工况下静力分析结果如图7所示。

图7 优化前和优化后的应力、位移对比

从图7以看出：优化后的新型跨越架最大Mises应力为113.83 MPa,相比于优化前减小了5.52 MPa,结构整体承载能力与优化前相当;跨越架结构最大位移为152.58 mm,比优化前减少了9.23 mm。

4 结 论

本文设计了一种移动展开式跨越架结构,通过有限元分析软件对整体结构进行了有限元计算,并利用萤火虫优化算法对该跨越架进行了尺寸优化。得到如下结论:

(1) 移动展开式跨越架可直接由载重汽车运至施工现场,液压顶升可实现架体的快速搭建,并且操作简便,可重复使用。

(2) 臂架上方可作为稳定过线平面,起到直接封网作用,大大减少了封网施工所耗费的时间和经费。

(3) 根据有限元计算结果可知,该新型跨越架结构的强度、刚度满足设计要求。

(4) 建立了基于萤火虫算法的跨越架结构优化模型,优化后的跨越架结构不仅减重率达到6.06%,且加强了结构的强度和刚度。

(5) 优化结果表明，本文基于萤火虫算法建立的移动展式跨越架结构优化模型能有效减轻结构质量,为跨越架提供了一种切实可行的优化设计方法。