不可靠通信条件下的CACC纵向控制仿真分析

王润民，卢 涛，宋晓鹏，张心睿

(1.长安大学 交通运输部认定自动驾驶封闭场地测试基地，陕西 西安 710018;2.长安大学 车联网教育部-中国移动联合实验室，陕西 西安 710064;3.浙江省交通规划设计研究院有限公司，浙江 杭州 310030)

0 引 言

协同式自适应巡航控制是在自适应巡航控制(adaptive cruise control，ACC)的基础上发展而来的。ACC主要利用安装在车身上的雷达等传感器测量前车的速度和间距，并根据这些信息控制油门和刹车，以保持和前车的安全距离。

而CACC基于车联网的汽车协同自动驾驶控制技术，通过车车之间相互通信传递车辆的速度、位置等信息，并综合多个车辆的信息设计分布式控制器，车辆可以以更小的间距行驶，从而提高通行效率。相对于ACC控制技术，CACC控制技术更加精确，而且抗干扰能力强[1]，因而备受关注。

具备CACC功能的车辆可以利用车车通信技术实时获取前车加速度状态，进而通过调节车头间距误差及速度差优化本车加速度输出，有望改善交通流运行质量，并在降低交通能耗、改善交通安全、提高交通效率等方面发挥重要作用[2-4]。

CACC跟驰模型的建模已成为交通流理论研究与智能交通系统的研究热点[5]，但是CACC对网络的稳定性有一定要求，构建CACC模型时，车联网稳定性应该作为一项重要因素。CACC系统的有效性依赖于基于车联网通信实现的车辆速度、加速度等信息实时、可靠交互，然而受各类天气条件及行车环境的影响，理想、可靠的通信环境难以在实际交通场景中实现[6]。因此迫切需要在不可靠通信条件下对CACC的适应性进行评估分析，以研究不可靠通信条件对CACC模型的影响。

目前对网联汽车队列的纵向控制研究主要集中在CACC模型的研究上，并且对于提出的CACC模型的有效性验证建立在车联网通信性能极好的情况下，大多未考虑不可靠通信条件下CACC模型的有效性。

如文献[7]基于恒定期望车间时距提出了一种CACC跟驰模型，但是模型仿真时没有考虑通信延迟和丢包率；文献[8]提出一种基于可变间距的CACC跟驰模型，通过改变前车加速度大小对CACC模型稳定性进行验证，没有考虑通信性能对CACC模型的影响；文献[9]从控制系统特性的角度，考虑了通信性能对CACC模型的影响，对CACC车辆跟驰行为建模方法进行了仿真研究，但是对与通信条件描述的不够具体。

针对上述问题，文中基于Veins仿真平台构建了仿真测试环境，以IEEE802.11p协议为CACC队列通信协议，以丢包率、时延作为构成不可靠通信条件的因素，对Rajamani、S. Santini、Ploeg三种CACC模型进行仿真研究，得到不可靠通信条件对三种CACC模型稳定性的影响。

1 网联汽车纵向控制模型分析

1.1 Rajamani控制模型

该模型是Rajamani等人[10]提出的一种CACC控制模型，车队中每辆车的加速度由下式给出：

1.2 S. Santini控制模型

该模型是S. Santini等人[11]提出的一种CACC控制模型，车队中每辆车的速度由下式给出：

(2)

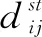
1.3 Ploeg控制模型

本模型是Ploeg等人[12]提出的一种CACC控制模型，车队中每辆车的加速度由下式给出：

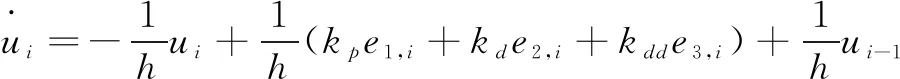
(3)

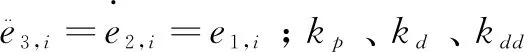
2 仿真平台搭建及测试方案设计

2.1 仿真环境构建及参数设置

Veins耦合了OMNeT++和SUMO，其中前者为网络仿真器，后者为交通仿真器，是一种典型的车联网仿真平台[12]。该文对Veins仿真平台进行参数设置，作为评估CACC模型的仿真测试平台。Veins基本交通参数设置如表1所示，形成的仿真界面如图1所示。

表1 交通基本参数设置

图1 CACC仿真界面

在OMNet++中实现车辆通信的仿真，车联网通信协议采用802.11p，是主流车联网通信协议之一[13]，其具体参数如表2所示。

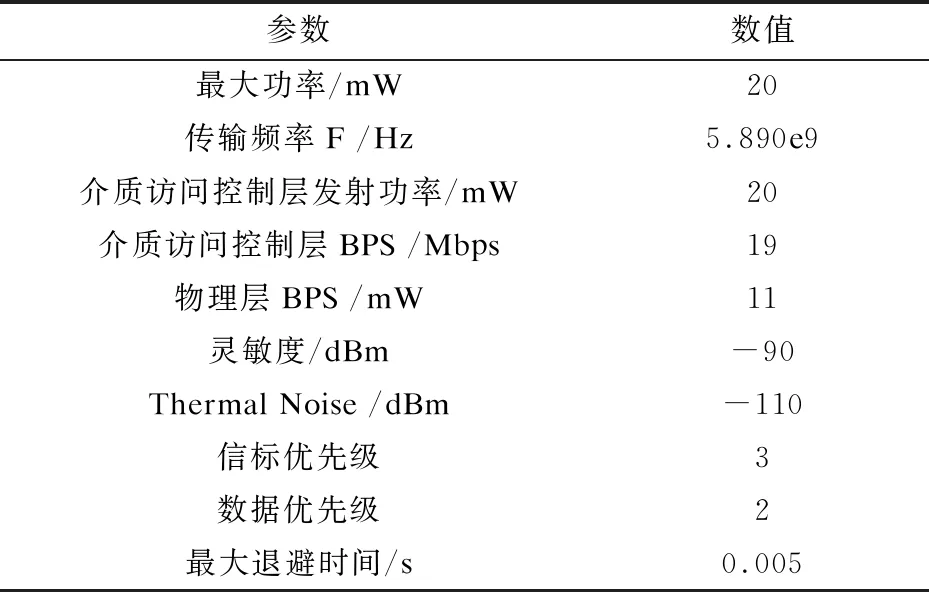
表2 IEEE 802.11p协议基本参数

2.2 测试方法设计

2.2.1 不可靠通信条件分析

在CACC系统运行中，多种因素都会对其稳定性造成影响，其中不可靠通信条件对CACC的稳定性及有效性造成影响。该文选取两个构成不可靠通信条件的影响因素：延迟和丢包率[14-16]，通过仿真CACC模型在不同延迟和丢包率下的运行情况对其进行测试分析。

(1)延迟(delay，DE)，延迟是数据包从源车辆正确传输到目标车辆所需要的时间，其平均值为平均延迟。在车联网环境下车辆跟驰速度快且跟驰间距小，这就要求车辆之间的通信延迟必须保持在极低的范围以内，因此这个指标对于CACC安全稳定具有特别重要的意义。

(2)丢包率(packet loss rate，PLR)，PLR为目标节点丢失的数据包与源节点应用层发送的数据包的比值关系，即丢失数据包的统计度量，主要体现了车联网的两个主要特性：网络可靠性、网络拥塞/通信状况。

2.2.2 测试方案设计

本研究在跟驰行驶和紧急刹车两种场景下，通过仿真改变延迟和丢包率对三种不同的CACC控制模型的性能表现进行测试。在跟驰场景下，头车车速正弦变化，初始车速为100 km/h、振幅为10 km/h、频率为0.2 Hz，后7辆车利用CACC控制模型跟随于头车，设置所有车辆相互之间发送车辆信息的丢包率为5%，仿真时间持续60 s，记录8辆车的速度信息；再将丢包率分别提升至10%、40%，重复仿真并记录所有车的速度信息；最后设置丢包率为0，所有车辆相互之间发送车辆信息的延迟为5 ms，仿真时间持续60 s，记录所有车的速度信息，再将延迟提升至10 ms、100 ms，重复仿真并记录所有车的速度信息。

在紧急刹车场景下，头车初始速度为100 km/h，5 s后开始以-8 m/s2的加速度减速，后7辆车基于设定的CACC控制模型跟随头车，设置所有车辆相互之间发送车辆信息的丢包率为5%，仿真时间持续60 s，记录8辆车的速度信息；再将丢包率提升至10%、40%，重复仿真并记录所有车的速度信息；然后设置丢包率为0，所有车辆相互之间发送车辆信息的延迟为5 ms，仿真时间持续60 s，记录所有车的速度信息；最后将延迟提升至10 ms、100 ms，重复仿真并记录所有车的速度信息。由于速度可以直观体现出队列中每辆车的状态变化，所以用速度作为指标用来研究丢包和延迟对CACC纵向控制仿真的影响。

3 仿真结果及分析

为了保证输出结果的可视化效果，实验中选取8辆车中的头车(1号车)、3号车、5号车、7号车来分析丢包和延迟对三种CACC控制模型造成的影响。

3.1 丢包率对CACC控制性能的影响

3.1.1 头车速度正弦变化场景

由图2(a)、(b)、(c)可看出，在丢包率相同的情况下，Rajamani控制模型跟驰效果最好，后车和前车速度几乎保持同步变化。而Ploeg控制模型跟驰效果最差，后车车速滞后于前车车速变化，并且速度大小也不能与前车车速保持一致，每一辆车的最大速度都小于前一辆车。S. Santini控制模型后车车速也相对滞后于前车车速变化，且车速小于头车，但除头车外后车车速能基本保持一致。

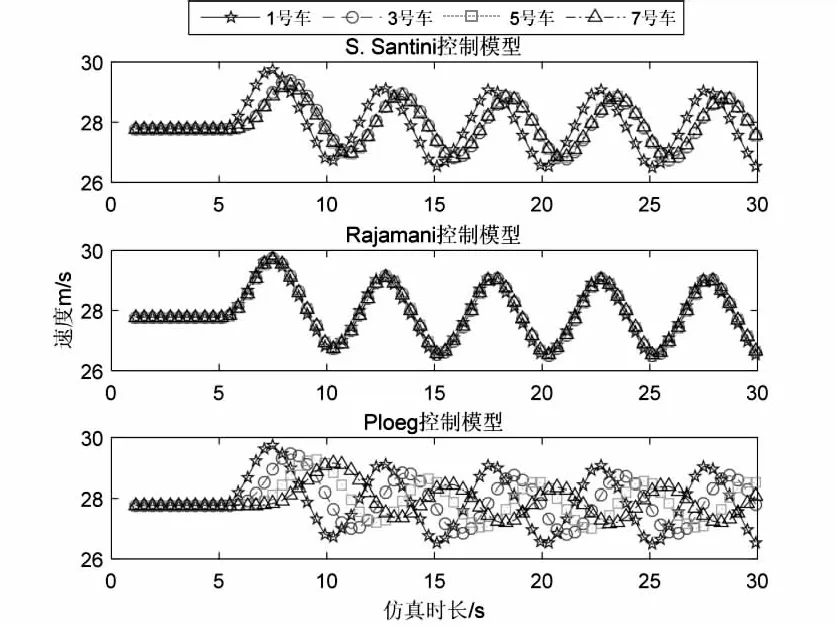
(a)丢包率5%

横向对比图2(a)、(b)、(c)可看出，随着丢包率增大，三种模型中跟驰车辆的速度变化都会滞后。

Rajamani控制模型和S. Santini控制模型速度滞后量相对较小，在40%丢包率情况下的速度变化比10%丢包率情况速度变化滞后0.5 s左右，Ploeg控制模型的滞后量较大，在40%丢包率情况下的速度变化比10%丢包率速度变化滞后1 s左右，且跟驰车辆速度最大值增加约0.2 m/s。由此可以看出，当头车速度正弦变化时，三种控制模型都会被丢包率影响，丢包率越大，跟驰车辆车速变化越迟，其中Rajamani控制模型受丢包率影响最小，Ploeg控制模型受丢包率影响最大。

3.1.2 头车紧急刹车场景

丢包对CACC控制模型紧急刹车情况下的影响基于图3所示的结果分析，由图3可知，当头车紧急刹车时，S. Santini控制模型中除头车外所有跟驰车辆过1 s左右开始减速，并且速度开始快速下降，降到大约7 m/s时速度下降变缓；Ploeg控制模型中每辆车比前车迟大约1 s开始减速，所有车辆速度均匀下降，大约4 s车速下降为0 m/s；Rajamani控制模型中所有车几乎同时开始刹车，并且车辆减速度几乎一致，车速在5 s内匀减速至0 m/s。通过对比图3(a)、(b)、(c)可知，随着丢包率增大，三种模型中跟驰车辆开始减速的时间都略微推迟0.1 s左右，受到丢包率影响区别不大。

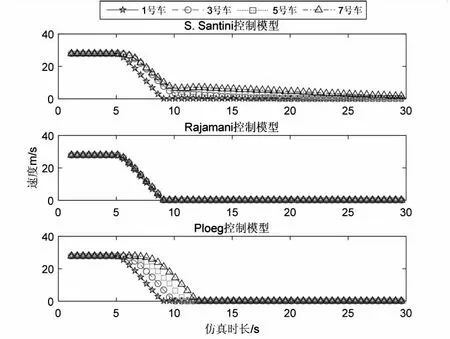
(a)丢包率5%

3.2 时延对CACC控制性能的影响

3.2.1 头车速度正弦变化场景

图4是通信延迟条件下头车车速正弦变化时车辆速度曲线图。由图4可知，通信延迟相同的情况下，Ploeg控制模型跟驰车辆车速变化明显落后于前车车速变化，Rajamani控制模型跟驰车辆速度变化与头车几乎相同，S. Santini控制模型跟驰车辆车速变化落后于头车，但是除头车外其余所有车辆速度变化几乎相同。对比图4(a)、(b)、(c)可知，通信延迟越大，跟驰车辆速度变化越不灵敏。

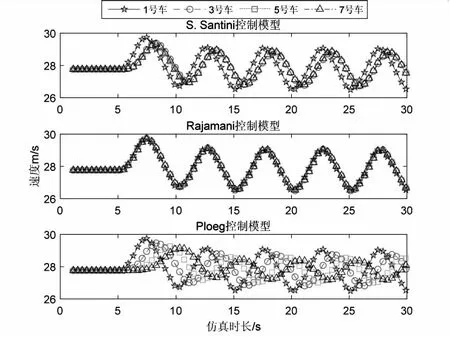
(a)通信延迟5 ms

总的来看，在头车速度正弦变化场景下，Ploeg控制模型更容易受到通信的延迟影响，Rajamani控制模型更稳定。

3.2.2 头车紧急刹车场景

头部紧急刹车的情况下不同通信条件车辆速度随时间变化的曲线图如图5所示。从图中可以看出，在通信延迟相同的情况下，Rajamani控制模型跟驰车辆车速变化延时较小，而S.Santini控制模型和Ploeg控制模型跟驰车辆车速变化都有较明显的延时，其中Ploeg控制模型延时最大。横向对比图5(a)、(b)、(c)可以看出，随着通信延迟的增大，跟驰车辆的速度变化延迟也会增大。

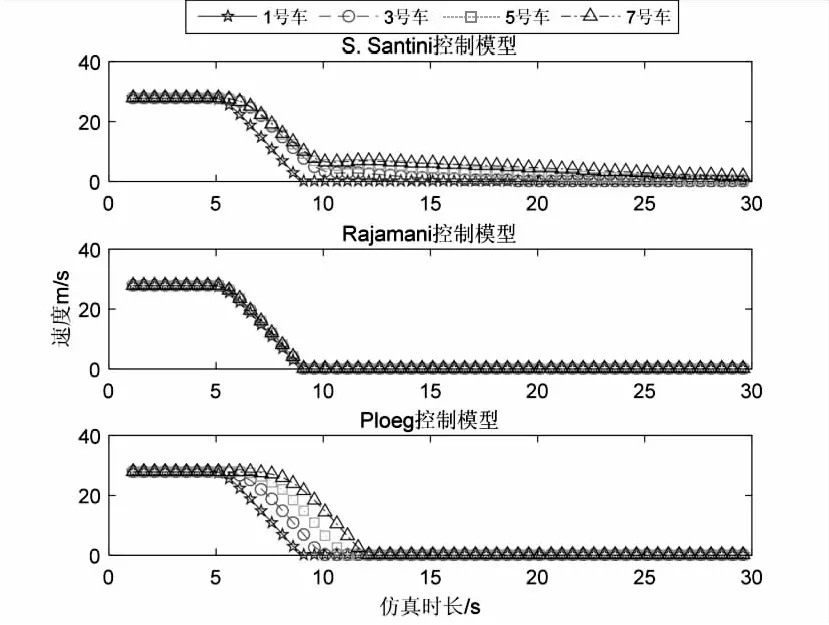
(a)通信延迟5 ms

总的来看，在头车紧急刹车场景下，Rajamani控制模型相对更加稳定，而Ploeg控制模型更容易受到通信的延迟影响。

4 结束语

基于Veins仿真平台，分别测试了丢包率和时延对S. Santini、Rajamani和Ploeg三种典型CACC模型控制性能的影响。针对头车速度正弦变化和头车紧急刹车两种情况分别测试了丢包率为5%、10%和40%下的车辆速度变化，测试结果表明：头车速度正弦变化时，Rajamani控制模型受丢包率影响最小，Ploeg控制模型受丢包率影响最大；头车紧急刹车时，三种模型中跟驰车辆开始减速的时间都略微推迟0.1 s左右，但受到丢包率影响区别不大。针对头车速度正弦变化和头车紧急刹车两种情况分别测试了延迟5 ms、10 ms和100 ms下的车辆速度变化，测试结果表明头车速度正弦变化时，Ploeg控制模型效果最差，最好的是Rajamani控制模型；头车紧急刹车与头车速度正弦变化测试场景下的测试结果类似，Rajamani控制模型表现最稳定，Ploeg控制模型稳定性最差，但三种控制模型跟驰车辆的速度变化延迟都会随着通信延迟的增大而增大。