内外不确定因素同时估计与补偿的鲁棒分布式跟踪控制

张 特李世尧朱 波

(1.电子科技大学航空航天学院,四川成都 611731;2.中山大学航空航天学院,广东广州 510275)

1 引言

与自主无人系统的单体控制相比,协同控制可以通过个体之间数据交互、协调合作提升任务的执行效率,且能够解决复杂环境中更具挑战性的任务,例如协同搜救、协同作战、编队巡航等[1–3].这些协同控制任务能够通过基于领航–跟随的分布式跟踪控制问题去描述,在大自然中存在的生物集群现象中已经证实了基于领航–跟随的系统能够加强群体中个体间的通信和定位,且存在节能的特性[4].因此,基于领航–跟随的分布式跟踪控制具有重要的研究意义[5].

在实际应用场景中,受复杂环境及传感器本身缺陷的影响,分布式跟踪控制方法的设计通常需要考虑到一些外部因素的影响.针对个体间在进行数据传输的过程中存在通信时滞现象,文献[6]研究了领航者在速度不变条件下多智能体时滞系统的领航–跟随一致性问题,文献[7]研究了基于网络的领航–跟随一致性,提出了一种基于网络的一致性控制协议,文献[8–9]研究了基于事件触发的多智能体线性时滞系统的领航–跟随一致性问题;文献[10–15]针对多智能体系统在输入受扰状态下的分布式一致性跟踪问题,其中文献[10–12]采用不确定与干扰估计器(uncertainty and disturbance estimator,缩写为UDE)[16–17]对不确定因素和干扰的力矩效应进行估计及补偿,文献[13]通过设计自适应控制律对外部扰动进行了补偿,文献[14–15]通过神经网络对不确定动态和输入扰动进行了估计和补偿;传感器在测量过程中极易受到外界影响产生测量噪声,针对此问题,文献[18–19]考虑状态受噪声影响的多智能体领航–跟随一致性问题,其中文献[19]通过时变增益减小噪声对系统的影响.

在领航者跟踪这种任务中,领航者和跟随者可能处在相同的干扰环境中.以多无人机协同跟踪目标无人机为例,领航无人机和跟随无人机往往都会受到气流干扰.针对这种情形,为了实现高精度的分布式同步跟踪,在为跟随者设计分布式控制器时,不仅需要考虑跟随者自身所受扰动对运动同步的影响,往往也需要补偿干扰对领航者运动的影响,以保证运动同步的快速性和准确性.然而,很多现有文献(例如文献[20–21])在为跟随者设计分布式控制律时,假定领航者的动态是不受干扰的,且没有挖掘跟踪误差最终界与核心设计参数之间的关系,导致参数调节缺乏理论指导.

为此,本文研究领航者和跟随者同时存在模型不确定项及受到外部扰动影响下的分布式同步跟踪问题,并以多架3–DOF直升机的角位置高精度鲁棒同步跟踪控制任务为例,进行控制律的设计、仿真验证及实验验证.该模型平台由加拿大Quanser公司提供,其角运动明显受建模不确定因素和外部干扰的影响(安装有独立的主动干扰系统(ADS),对升降通道的运动影响明显),是良好的鲁棒控制验证平台[12,22–23].

本论文的技术贡献如下:1)分析了领航者的干扰和跟随者自身的不确定因素对同步跟踪影响的差异性,设计不同的低阶估计器(基于速度测量的二阶ESO和一阶UDE),以修正分布式跟踪控制律中的前馈项,并补偿自身的不确定因素,从两个方面提升同步跟踪精度;2)采用统一的奇异摄动理论框架分析了ESO和UDE的核心参数对同步跟踪误差稳态界的影响,为实现简单的跟踪性能调节提供了保证.3)构建了包含两架实物3–DOF直升机模型的面向协同控制算法验证的“虚实结合”实验环境,“虚”是指环境中包括纯数字模型作为节点,“实”是指环境中包括一定数量的物理实体作为节点,如图1所示.设计了四组对比实验,证实了内外不确定因素同时补偿的必要性,也验证了调参方法的有效性.

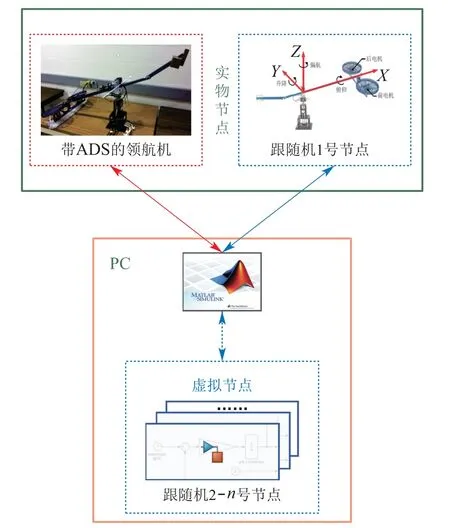
图1 “虚实结合”实验架构Fig.1 The architecture for experimental verifications with both virtual and real helicopters as nodes

2 模型简化与问题描述

2.1 模型简化

参考文献[24],针对第i架3–DOF直升机的升降通道和俯仰通道(本论文不考虑偏航通道的控制问题),采用拉格朗日法建立的多刚体模型为

其中:αi和βi分别代表升降角和俯仰角,Vfi和Vbi分别为作用在前向电机和后向电机的电压,mi表示俯仰通道的有效重量,lbi表示平衡杆和直升机本体的距离,cαi,cβi分别表示升降和俯仰通道的粘滞阻力系数,i=0代表领航机,i=1,···,n代表跟随机,Jei和Jpi分别代表升降通道和俯仰通道的转动惯量,其余参数的物理含义及单位参考文献[10].

为了方便控制器的设计,将模型(1)简化为

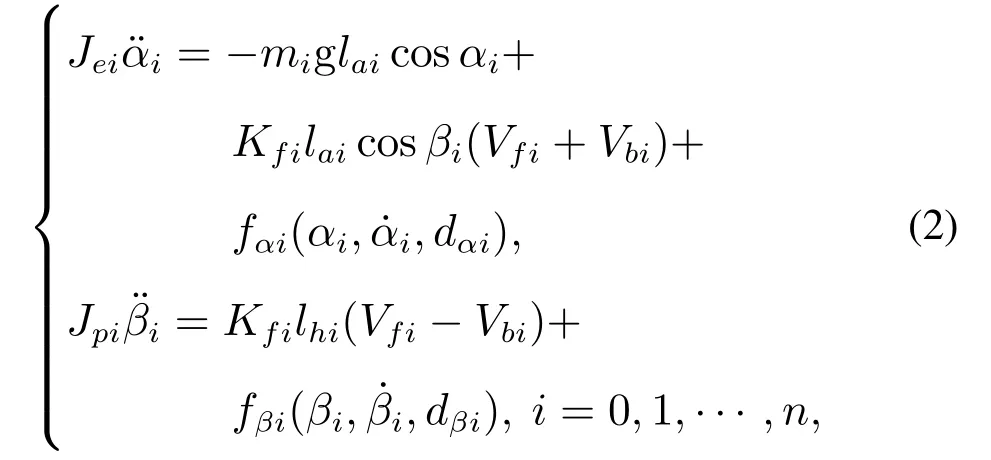
其中fαi和fβi分别表示升降通道和俯仰通道的集总扰动.注意到式(1)中忽略了两项,其中速度的阻尼项可以视为模型的不确定项,另一项把它当作系统的有界时变干扰.除此之外,为了使得本文的设计能够不仅限于3–DOF直升机的模型特性,考虑在扰动中加入角度阻尼项增加设计的普适性.因此,两个通道的集总扰动分别表示为

其中Δαi,Δα˙i,Δβi,Δβ˙i为有界常数.

对每架3–DOF直升机模型(2),考虑以下输入变换

通过以上变换,升降运动和俯仰运动的非线性动力学模型可进一步简化为

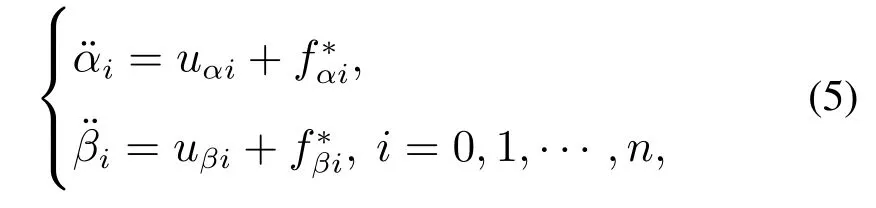
其中简化后的扰动为

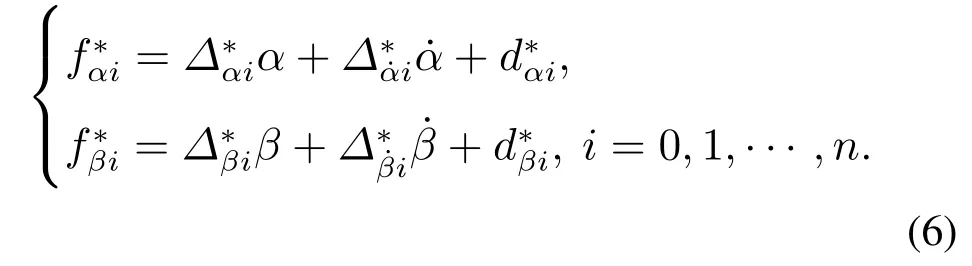
至此,通过反馈线性化实现了对每架3–DOF直升机的输入输出反馈线性化.进而由uαi,uβi可计算出前向电机和后向电机电压为

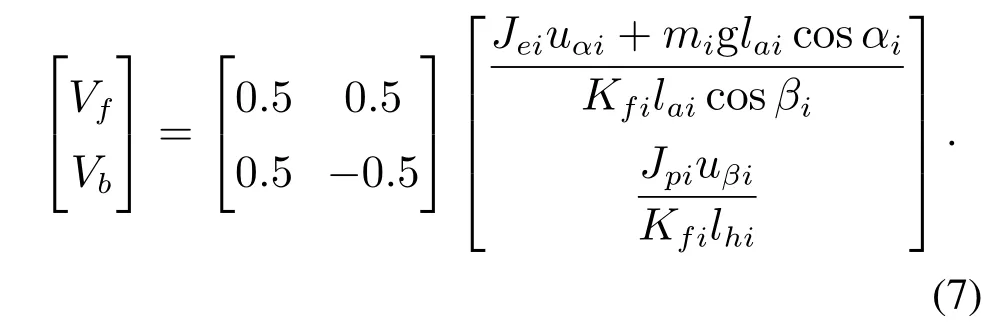
2.2 问题描述

在本文中,利用代数图G=(V,E,A)对3–DOF直升机之间的通信结构进行建模,其中,V={v1,v2,···,vn}为图G的节点集,E ⊆V ×V为边集.若{vj,vi}∈E,则节点vj为vi的邻居.A=[aij]∈Rn×n是权重为aij≥0的邻接矩阵,其中,aii=0,aij >0 当且仅当{vj,vi}∈E.若存在一个与其它节点都连通的节点,这个节点被称作根节点,图G则存在有向生成树.

定义图G的Laplacian矩阵为L=D −A,其中D为图G的入度矩阵.对于本文考虑的轨迹跟踪问题,通信拓扑G¯包含n+1个智能体,其中n个智能体为跟随者,另外一个为领航者.定义矩阵B¯=diag{b1,b2,···,bn},若智能体i能够获取领航者的信息,bi >0,否则bi=0.

考虑以多个3–DOF直升机为节点构成的多智能体系统,其中n个跟随机模型由系统(5)给定,节点之间的拓扑结构满足如下条件.

假设1存在一个有向生成树,其中领航者为根节点.

由系统(5),领航机的动力学模型为

下面,给出跟随机和领航机的输入扰动满足的有界性和光滑性条件.

考虑系统(5)中两个通道具有相同的形式,为了方便后续的分析,定义新的变量y ∈{α,β}.同时定义跟踪误差函数为

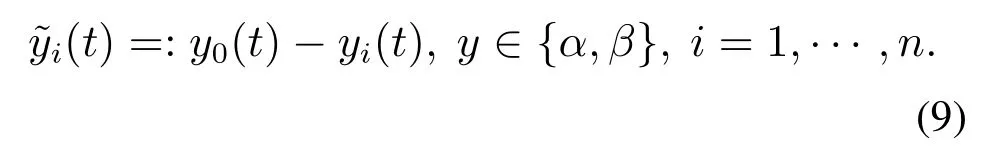
定义1在跟随机的集总扰动的条件下,跟踪误差满足

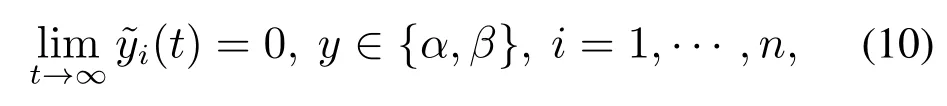
则称系统(5)实现了渐近跟踪.

定义2在其他条件下,跟踪误差满足

则称系统(5)实现了近似渐近跟踪.其中:ς是一个正常数,代表的最终界,tς是对应的调节时间.

为了公式的简洁和清晰,后续内容将省略公式中的变量y ∈{α,β}和节点i=1,···,n.

3 控制器设计

定义局部邻居同步误差(local neighborhood synchronization error,LNSE)

3.1 渐近跟踪控制器µyi设计

通过上述对控制器结构的分析,在不考虑自身扰动的条件下,µyi可设计为

由式(5)(8)(12)(18)和式(21),可得LNSE的节点动态方程为

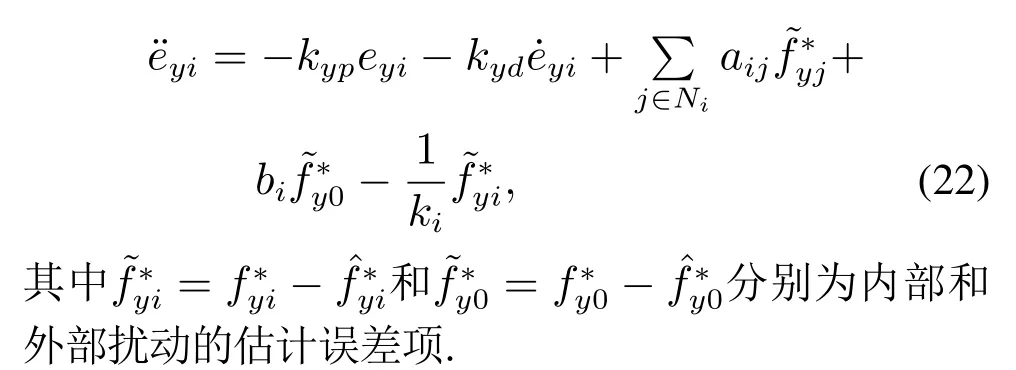
考虑到扩张状态观测器不需要控制器结构的特性,对领航机输入扰动的估计策略设计采用此方案能够降低机间通信的负担.因此,采用如下二阶线性扩张状态观测器[25–26]对领航机输入扰动进行估计.

3.2 干扰估计设计

与对领航机集总输入干扰(外部扰动)的估计不同,跟随机对自身集总输入干扰(内部扰动)的估计无需考虑机间通信压力,考虑到UDE相较于ESO有以下典型优势:1)最大程度利用了系统模型信息,能够更加准确的估计集总输入干扰;2)相较于ESO存在多个设计参数,UDE的设计参数更少[16,27],且参数决定了UDE的估计带宽,调参更为简单.本文采用UDE对跟随机的输入干扰进行估计与补偿,UDE的核心思想是干扰估计信号与原干扰信号存在如下滤波关系:

注意到,式(26)中的角加速度项为3–DOF直升机不可测的物理量,为了保证上述系统的物理可实现性,即通过设计G(s)使得式(26)的等效计算式避免使用角加速度信息.考虑设计滤波器G(s)为

通过上述控制器的设计与分析,结合节点闭环系统(22)和(32),可以得到第i个跟随机的闭环系统控制结构如图2所示.

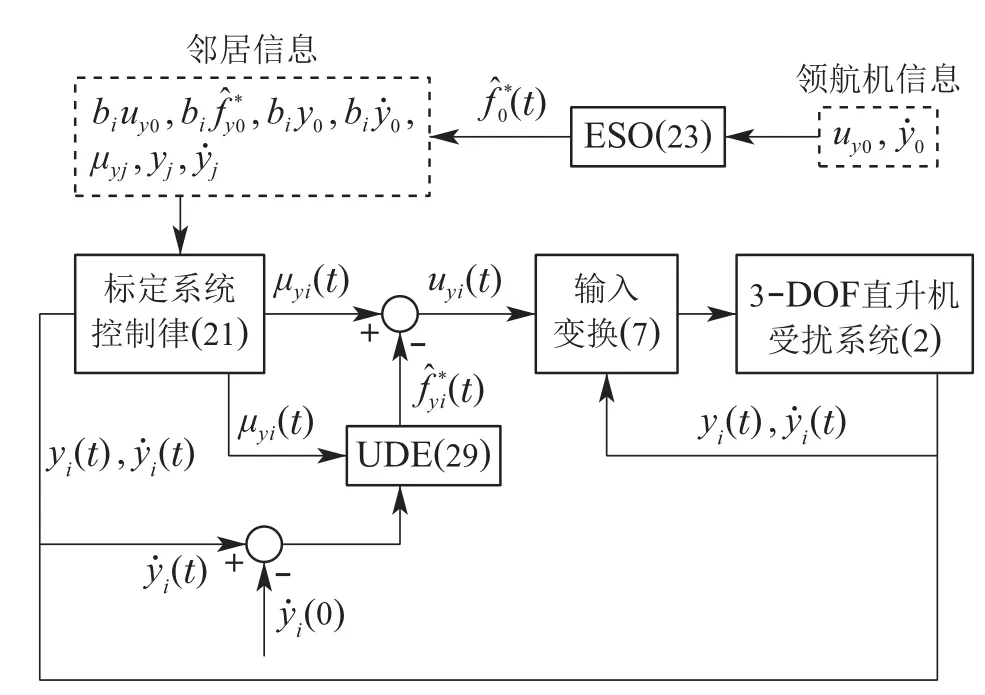
图2 第i架跟随机的鲁棒控制结构图Fig.2 The proposed robust control configuration for the i-th helicopter

4 系统稳定性及UDE性能分析

为了方便后续分析,定义如下变量:

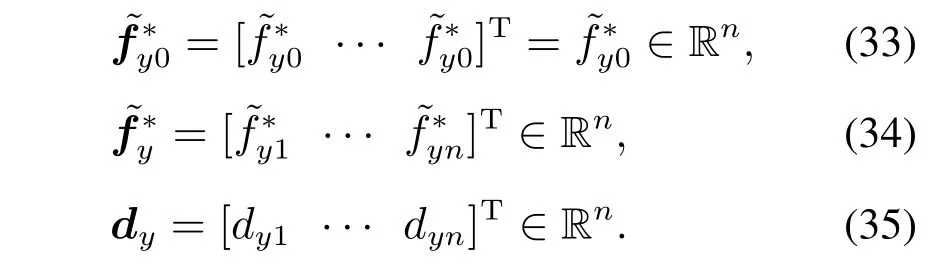
由LNSE节点动态方程(22)可得其网络动态方程为

同理,结合方程(36),UDE的节点估计误差方程(32)可进一步表示为网络估计误差方程

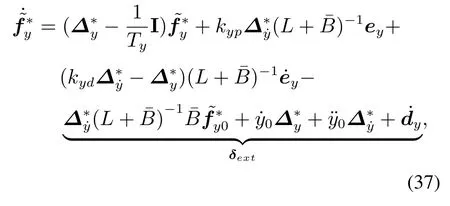
证考虑到误差系统(36)和(37)存在状态间的耦合关系,为了便于进一步的分析,将估计误差方程(37)两端同时乘以设计参数Ty,联立LNSE的动态方程(36),可以得出如下两个子系统构成的标准奇异摄动方程

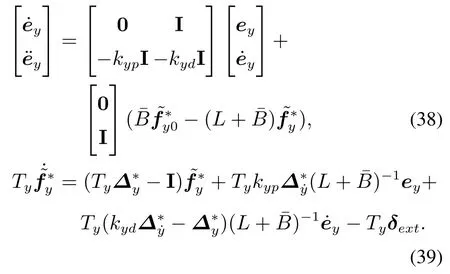
首先,对于1),本文将利用文献[28]中的定理11.4进行证明.假设系统的所有外部信号为0,即δext=0,,那么系统(38)简化为

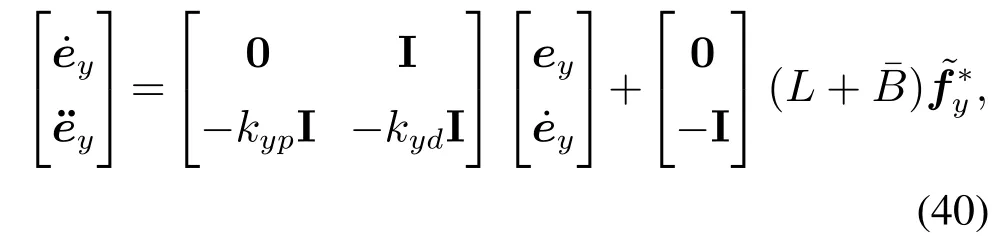
同理,系统(39)简化为

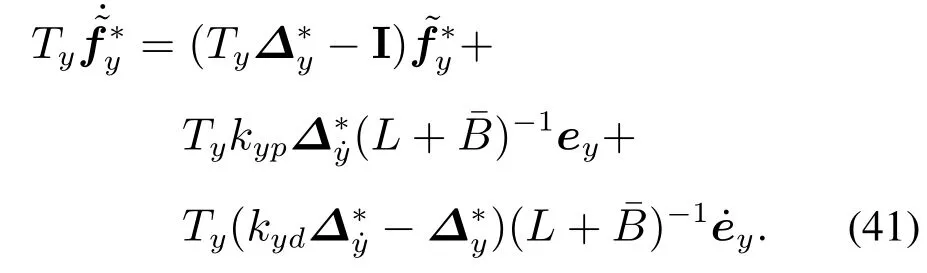
显然,式(42)有一个位于原点的孤立根,将此根代入式(40)可得

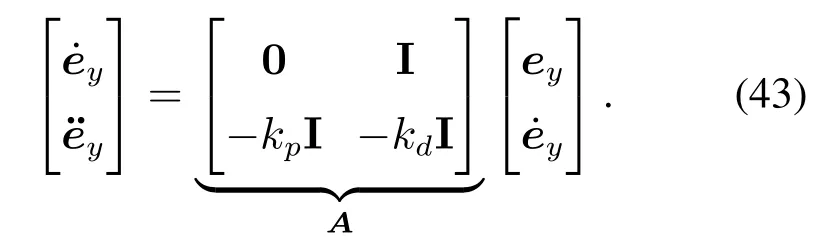
因此,通过最终界函数选取ς=Ty得证本定理的2)和3). 证毕.

值得注意的是,本文通过最终界(ultimate bound)的概念来刻画观测器和估计器的估计精度,分别通过引理2和定理1给出了观测器与估计器的估计误差的最终界与设计参数(σy和Ty)之间的关系.具体来说,引理1中的第2条结论和定理1证明中的式(50),简洁明了的指出了估计误差的最终界大小与设计参数大小之间存在正比的关系,即设计参数越小,估计误差的最终界越小,估计精度越高.

设计参数满足Ty >0,上述系统是输入状态稳定的.当,系统(53)会逐渐退化为非受迫系统,系统状态渐近收敛到零,1)得证.同理,在满足1)的条件下,由引理2,系统(36)也退化为非受迫系统,2)得证. 证毕.

定理2在定理1的基础上给出了UDE实现渐近估计和系统实现渐近跟踪需要满足的条件.

5 仿真及实验验证

本节首先将通过数值仿真实验验证本文控制策略与参数调节机制的有效性;进一步,开展包括Quanser公司的3–DOF直升机实验平台的实验验证.在实验环节仅有两架3–DOF直升机实验平台,为体现出分布式控制背景,融合两架硬件实物平台“(实”节点)和两个直升机Simulink数字模型(“虚”节点)进行包括四个节点的“虚实结合”实验.

首先给出本文仿真实验与“虚实结合”实验的实验条件,升降通道的动态系统中的相关参数值参考文献[12],领航机的控制器结构为PD加前馈的形式,且其期望信号为

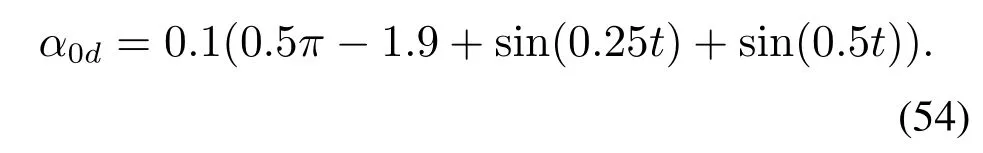
在“虚实结合”实验中,3–DOF直升机平台的扰动来源于其本身模型简化和辨识误差带来的模型不确定项,ADS以及传感器、环境等因素的干扰;在数字仿真实验中,所有仿真模型的数字扰动和模型不确定项均为

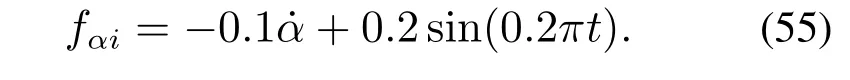
领航机和跟随机升降角初值分别为(单位为度)

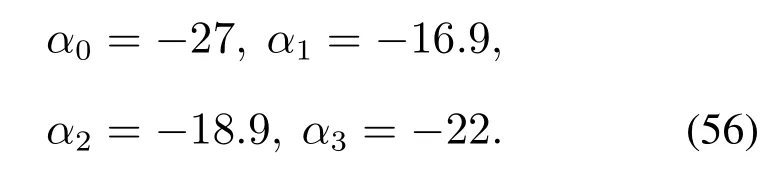
控制器(21)中的反馈增益分别为

ESO中的设计参数分别为

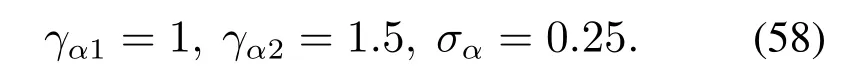
UDE的设计参数为

由于本文面向的问题是跟随机基于内外部扰动的同时补偿的分布式领航者跟踪控制,为了便于对比内外部扰动和估计器参数对系统整体跟踪性能的精度影响,以升降通道的跟踪控制为例,仿真实验与“虚实结合”实验均考虑以下4种对比方案:

方案1:一号跟随机仅通过ESO对外部扰动进行补偿(不补偿自身的模型不确定因素),其余跟随机通过UDE对自身模型不确定因素进行补偿.

方案2:一号跟随机仅通过UDE对内部扰动进行补偿(不补偿外部参考加速度中的不确定项,即不修正领航者的加速度信息),其余跟随机通过UDE对自身模型不确定进行补偿.

方案3:一号跟随机同时通过ESO和UDE同时对内外扰动进行补偿,其余跟随机通过UDE对自身模型不确定进行补偿.

方案4:相较于方案3,取更小的观测器和估计器参数,验证小参数下的性能,观测器和估计器参数分别调节为σα=0.1,Tα=0.2.

5.1 仿真实验

数值仿真的拓扑结构如图3所示,结果如图4–7所示.图4为方案1的仿真实验结果,由于一号跟随机没有对其内部扰动进行估计与补偿,其内部的扰动和不确定项会显著影响其跟踪精度,而二、三号跟随机通过获取一号跟随机的标称控制器信息,补偿了领航机外部扰动的同时又通过UDE估计并补偿了自身的扰动与不确定项,因此,在该方案中二、三号机的跟踪效果显著优于一号机.

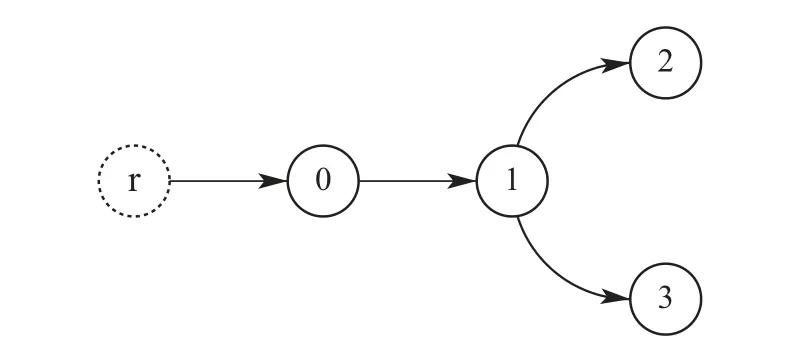
图3 通信拓扑结构Fig.3 The considered communication topology

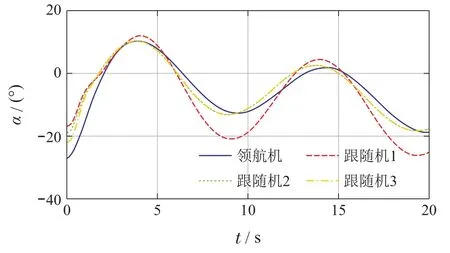
图4 仿真方案1领航机和跟随机的升降角轨迹Fig.4 The elevation angle trajectories of leader and followers for simulation case 1

方案2的仿真结果如图5所示,由于一号跟随机没有对领航机的扰动进行估计与补偿,该外部扰动会显著影响其跟踪精度;由于二号和三号跟随机的控制输入包括一号跟随机的标称控制器信息,该扰动会同时影响二号跟随机和三号跟随机的跟踪精度,但是三台跟随机均通过UDE对自身扰动进行了估计与补偿,因此三台跟随机的轨迹随时间收敛且与领航机存在较大跟踪误差.

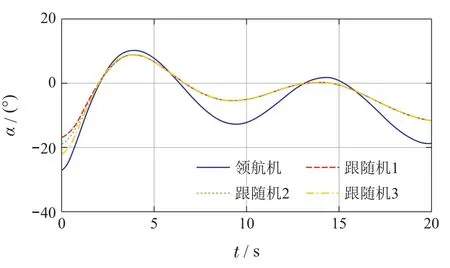
图5 仿真方案2领航机和跟随机的升降角轨迹Fig.5 The elevation angle trajectories of leader and followers for simulation case 2

在方案3中,一号跟随机同时对领航机和自身的扰动进行了估计与补偿,二号和三号跟随机对自身扰动进行了估计和补偿.由图6可以看出,相较于方案1和方案2,整体得跟踪性能有了大幅提升,但ESO和UDE的设计参数值较大影响了二者对内外扰动的估计精度,因此3台跟随机与领航机的轨迹存在一定的的跟踪误差.

图6 仿真方案3领航机和跟随机的升降角轨迹Fig.6 The elevation angle trajectories of leader and followers for simulation case 3

方案4的仿真结果如图7所示,与方案3相比,该方案调小一号跟随机中ESO的设计参数的同时调小3台跟随机中UDE的设计参数.实验结果显示出3台跟随机对领航机的高精度轨迹跟踪效果,证实了观测器和估计器的调参方案的有效性.

图7 仿真方案4领航机和跟随机的升降角轨迹Fig.7 The elevation angle trajectories of leader and followers for simulation case 4

5.2 “虚实结合”实验

“虚实结合”实验结构如图8所示,包括两个由Quanser公司的3–DOF直升机实验平台的“实”节点和两个Simulink仿真中的数字“虚”节点.“虚实结合”实验结果如图9–12所示.对比仿真实验结果可以看出,整体趋势上二者存在一定的差别,这是因为在“虚实结合”实验中,领航机的扰动主要来源于ADS系统,跟随机的扰动来源于模型简化和辨识误差带来的模型不确定项、环境干扰等因素;而在仿真实验中,外部干扰信号和模型不确定项是人为设计的.但是通过对比“虚实结合”实验与数字仿真实验的结果可以发现,虽然在轨迹趋势上有所不同,但整体的实验效果一致,同样论证了同时对内外扰动进行补偿的必要性和参数调节机制的有效性.

图8 “虚实结合”实验结构图Fig.8 The experimental verification including both virtual and real 3–DOF helicopters as nodes

图9 实验方案1领航机和跟随机的升降角轨迹Fig.9 The elevation angle trajectories for experimental verification 1

通过以上两种不同形式的实验验证,说明了针对多运动体的同步跟踪控制问题,跟随者在同时受内外扰动影响下,分别通过设计ESO和UDE对其进行估计和补偿是必要的,能够大大提升跟随者对领航者的跟踪性能,且参考引理2和定理1的结论,通过对估计器与观测器进行参数调节能够进一步提升跟踪精度,从而说明了本文设计的基于内外扰动同时估计与补偿的分布式鲁棒跟踪控制器以及参数调节机制的合理性与有效性.

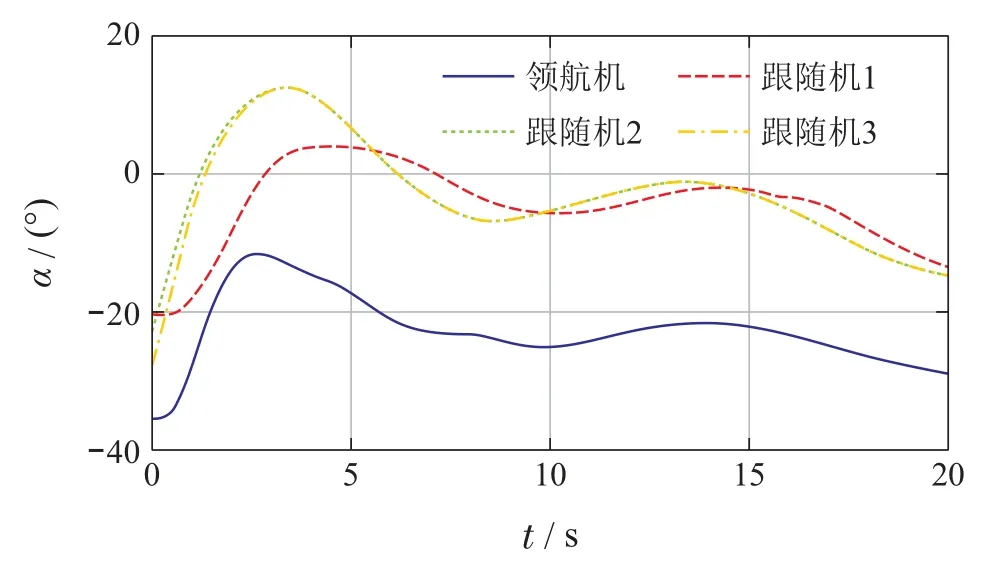
图10 实验方案2领航机和跟随机的升降角轨迹Fig.10 The elevation angle trajectories for experimental verification 2

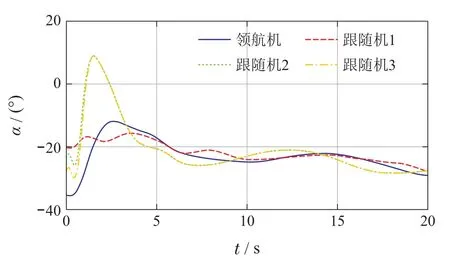
图11 实验方案3领航机和跟随机的升降角轨迹Fig.11 The elevation angle trajectories for experimental verification 3

由于篇幅的限制,俯仰通道仿真实验与“虚实结合”实验方案1–4的结果见网页https://blog.csdn.net/simatete/article/details/109057486.

图12 实验方案4领航机和跟随机的升降角轨迹Fig.12 The elevation angle trajectories for experimental verification 4

6 结论

本文以3–DOF直升机模型为例,研究了多运动体系统在同时受内外扰动影响下跟随者的鲁棒跟踪控制问题.重点设计了针对领航者扰动和自身不确定因素的估计器,包括基于速度测量的二阶ESO和一阶UDE.采用了奇异摄动理论分析了ESO和UDE的核心参数对同步跟踪误差稳态界的影响,并给出了渐近跟踪的条件.数字仿真及“虚实结合”实验结果证实了内外干扰同时补偿的必要性,以及参数调节机制的有效性.无速率测量条件下3个运动自由度的鲁棒同步控制设计将是下一步要考虑的问题.