二阶非线性多智能体系统有限时间分布式优化

娄如思,王璐瑶,马 丹

(东北大学信息科学与工程学院,辽宁 沈阳 110819)

1 引言

多智能体系统是多个具有独立运算、存储、通信等能力的个体通过信息交互共同完成一定任务的动态系统.这类系统能较好地描述互联多个体的复杂行为、多智能体系统的一致性、分布式优化、编队控制及其鲁棒性等问题[1–4],近年来受到国内外学者的广泛关注.

多智能体系统的优化是指每个智能体都存在一个目标函数,通过相邻智能体之间的通讯和协调,最小化所有智能体目标函数的和.随着动态系统中智能体数量的增加,复杂的地理环境以及通讯网络的大量使用,集中式控制不再适用于解决多智能体系统的优化问题.取而代之的是只需要自身和邻居智能体的信息,且在计算量、运行成本、可扩展性、鲁棒性等方面有着巨大优势的分布式控制.分布式优化问题广泛应用于智能电网的经济调度[5]、传感器网络的参数估计[6]、网络中的资源分配[7]等实际工程中.

Yang等[8]针对多智能体系统的分布式优化问题进行了综述,并将其应用到能源系统的最优协调问题.基于梯度的算法也广泛应用于解决多智能体系统的分布式优化问题.Tsitsiklis等[9]首先提出了基于梯度的分布式优化算法解决凸优化问题.Feng和Hu[10]考虑了负梯度方法设计非光滑的控制协议研究一阶多智能体系统的分布式凸优化问题.Lu和Tang[11]针对无向连通拓扑图提出了分布式Zero-gradient-sum(ZGS)算法,并证明了该算法能够指数收敛到全局最优解.Guo和Chen[12]将ZGS算法延伸到强连通且加权平衡的有向图中.

然而,在许多工程应用中,往往要求在有限时间内达到指定的性能,这对多智能体系统分布式优化也提出了挑战.Lin等[13]结合有限时间理论,研究了切换拓扑下具有约束的一阶多智能体系统的有限时间分布式优化问题.Song和Chen[14]在文[11]的基础上,将ZGS算法拓展到有限时间分布式ZGS算法.在实际系统中不可避免的存在干扰或未知信息等情况,为了保证系统的鲁棒性,研究存在干扰的非线性多智能体系统的分布式优化问题极具有实践意义.Wang等[15]和Wang和Hong[16]针对具有干扰的一阶多智能体系统,设计分布式优化控制器处理多智能体系统的优化问题.Liu等[17]结合小增益方法研究非线性多智能体系统的优化问题.Huang等[18]研究时变的通讯拓扑图下非线性多智能体系统的时变凸优化问题.以上研究都是针对低阶多智能体系统,二阶及高阶非线性多智能体系统分布式优化问题[19–20,24]的研究还不够充分.

本文结合实际系统中非线性和未知参数的广泛存在,考虑一类具有未知参数的二阶非线性多智能体系统.兼顾工程实际中的有限时间实现最优调节等需求(如智能电网),研究固定拓扑下,二阶非线性多智能体系统的有限时间自适应分布式优化问题.在提出的加速智能体状态收敛至目标函数最优解的控制策略下,给出一种基于幂积分方法的光滑的自适应分布式控制协议,保证在给定惩罚因子下,多智能体的状态在有限时间达到目标函数的最优解的邻域.最后,通过仿真验证了理论结果的可行性和有效性.

2 问题提出

考虑具有未知参数的二阶非线性多智能体系统

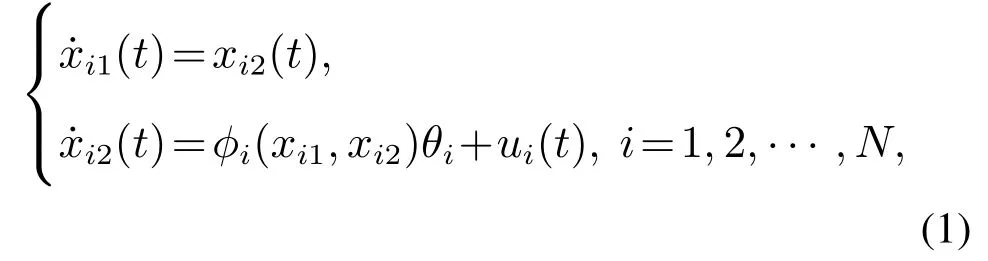
其中:xi1和xi2分别表示第i个智能体的位置和速度;ui表示第i个智能体的控制输入;φi(xi1,xi2)∈R1×l表示已知的非线性向量函数,θi ∈Rl×1表示未知的常参数,l是一个正常数.

第i个智能体的局部目标函数如下:

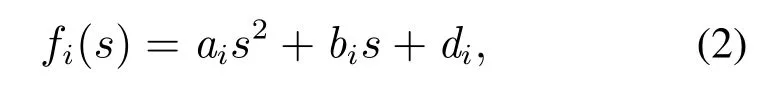
其中ai,bi,di是标量,且满足ai >0.自变量s表示第i个智能体的状态分量xi1(t).则多智能体系统(1)的总体目标函数定义为N个智能体的局部目标函数的和

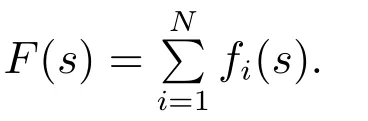
本文的目标是找到下列优化问题的最优解:

本文考虑智能体之间只能通过通讯拓扑和其邻居进行通讯,即第i个智能体只能获取自身的目标函数fi(s),不能通过通讯拓扑获取邻居的目标函数.在实际工程系统中,如网络的资源分配问题、智能电网的经济调度问题等,均将局部目标函数解释为代价(成本)函数,每个个体都具有一个代价(成本)函数,则整个系统的总代价(成本)由系统中所有个体的代价(成本)函数和来表示,所要达到的目标就是代价(成本)函数的和最小.

这里考虑固定无向连通的拓扑.本文将通过设计有限时间自适应分布式控制协议ui(t),i=1,2,···,N,使多智能体状态分量xi1(t),i=1,2,···,N在有限时间内达到最优解s∗的邻域.

定义1考虑多智能体系统(1),对于任意初始状态,若存在一个正常数T和一个充分小的正标量r,使得∀i,j=1,2,···,N,满足

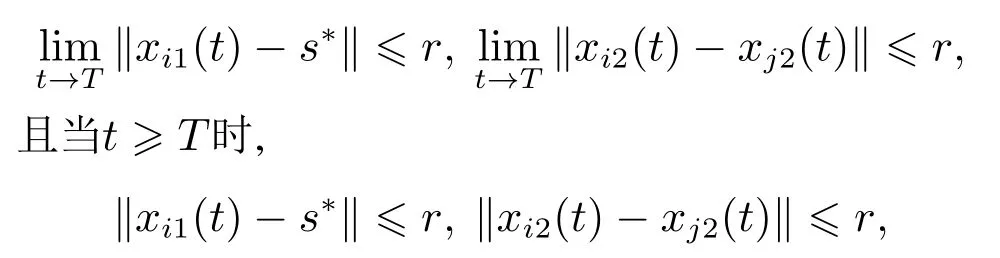
则称多智能体系统(1)能达到有限时间实用一致.

当位置状态达到一致时,则有

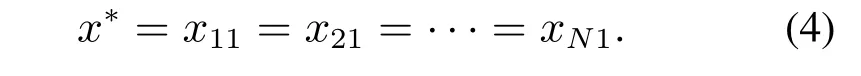
因此,问题可转化为求解具有等式约束的凸优化问题:

其中:βm >0,m=1,2,···是常数惩罚因子,第2项是惩罚项,惩罚项和位置状态与通讯拓扑图的拉普拉斯矩阵相关.当多智能体系统(1)达到实用一致时,惩罚项为0.

下面的引理将在主要结果中使用.

引理4[24]考虑一类非线性系统x˙=f(x,u),假设存在一个C1类的函数V(x):D →R,定义域D ⊂Rn,存在正实数α>0,0<γ <1,以及0<η <∞,如果V(x)在定义域D内正定,且V(0)=0,满足如下不等式:

则称非线性系统是半全局有限时间实用稳定的,若D=Rn,则系统是全局有限时间实用稳定的.

下面,基于构造的惩罚函数(6)给出一个新的控制策略,使得多智能体系统(1)的位置状态xi1(t)更快地收敛至优化问题(3)的最优解s∗.

步骤1给定一个较小的初始惩罚因子βm >0,惩罚因子的放大系数c>1,置m=1.

步骤2设计有限时间分布式控制协议ui(t),使得惩罚函数的负梯度(此时为βm的函数)在有限时间收敛至零的邻域内.

步骤3当惩罚函数的负梯度收敛至零的邻域内时,置βm+1=c ∗βm,返回步骤2,直至βm不再影响分布式控制协议ui(t).从而多智能体系统(1)的状态xi1(t)趋近于最优解s∗的邻域内,即≤r.

3 主要结果

本节将针对控制策略中的步骤2,设计有限时间分布式控制协议ui(t)和自适应律,使得惩罚函数(6)的负梯度在有限时间收敛至原点的邻域内,从而保证多智能体系统(1)在有限时间趋于最优解s∗的邻域.

定理1考虑无向连通拓扑下,多智能体系统(1)在有限时间分布式控制协议

下面,基于反步法,采用幂积分技术逐步设计虚拟控制协议,并最终获得分布式控制协议ui(t),使得惩罚函数(6)的负梯度在有限时间内收敛至原点的邻域内.

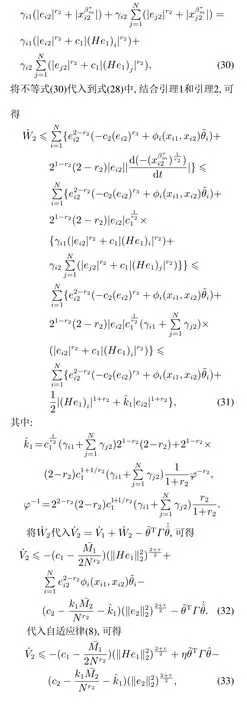
结合定义1和引理4,可知,在有限时间分布式控制协议(7)和自适应律(8)共同作用下,惩罚函数(6)的负梯度在有限时间收敛至原点的邻域内,即多智能体系统(1)的所有状态x1(∞)趋近于最优解s∗.

4 仿真分析

考虑一类由4个二阶非线性智能体构成的多智能体系统

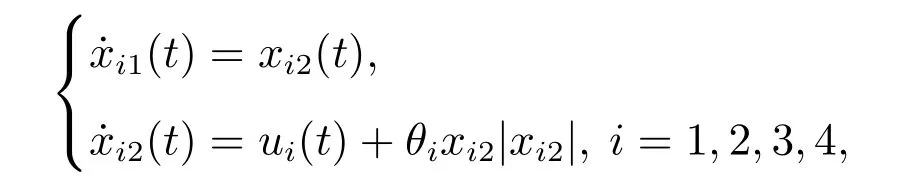
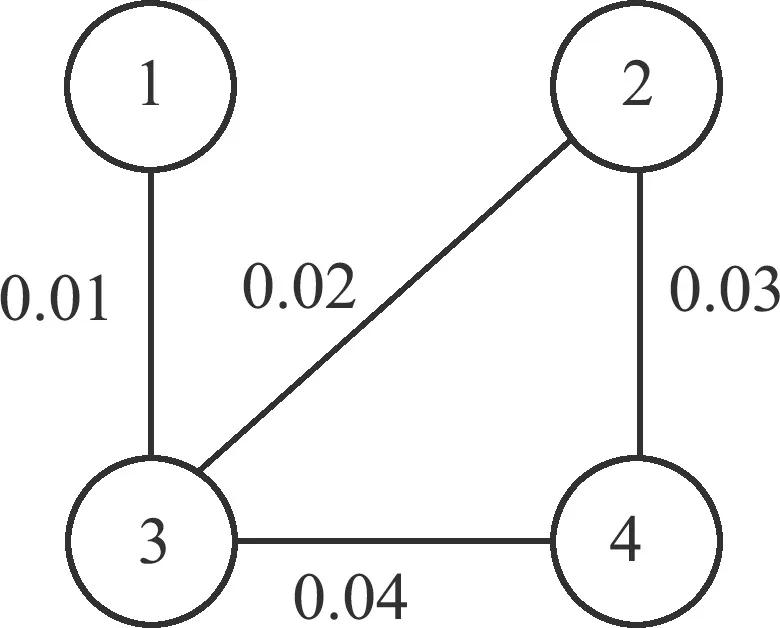
图1 通讯拓扑图Fig.1 Communication topology

其对应的拉普拉斯矩阵L由图1可得.给定4个智能体各自的目标函数分别为

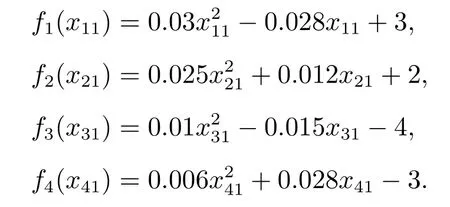
根据定理1,采用分布式控制协议为

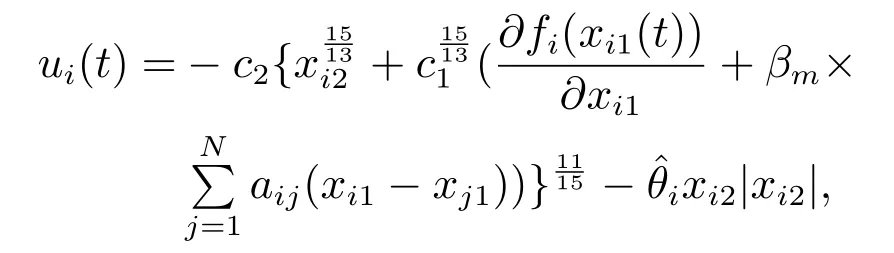
以及自适应律

给定初始参数c1=4,c=3,p=2,q=15,c2通过计算可以获得,c2参数依赖βm的取值.控制器参数选择具体如表1所示.

表1 控制协议具体参数Table 1 Controller parameters

则系统的状态轨迹由图2和图3给出.

由图2可以直观的看出多智能体系统的状态xi1经过有限次选取βm,最终收敛到最优解s∗的邻域内.每更新一次βm,多智能体系统的状态xi1都进一步的汇聚,最终收敛至最优解s∗的更小的邻域内.图3给出了系统的状态xi2,因为非线性函数中含有系统的状态xi2,导致在更新βm时状态xi2产生波动,经过短暂的参数调整之后,状态xi2开始快速的收敛到一致.选择同一初始条件,采用文献[10]中利用符号函数设计的算法,如图4所示.与文献[10]中协议相比,本文基于幂积分方法设计连续光滑的分布式控制协议可加快系统的收敛速度.与高阶多智能体系统一致性协议[24]相比,本文提出的协议使得多智能体系统达到一致后,一致性的状态滑向目标函数(3)的最优解.图5给出了自适应参数误差的仿真曲线,从图中可以发现,参数误差最终趋于常数,且保持不变.

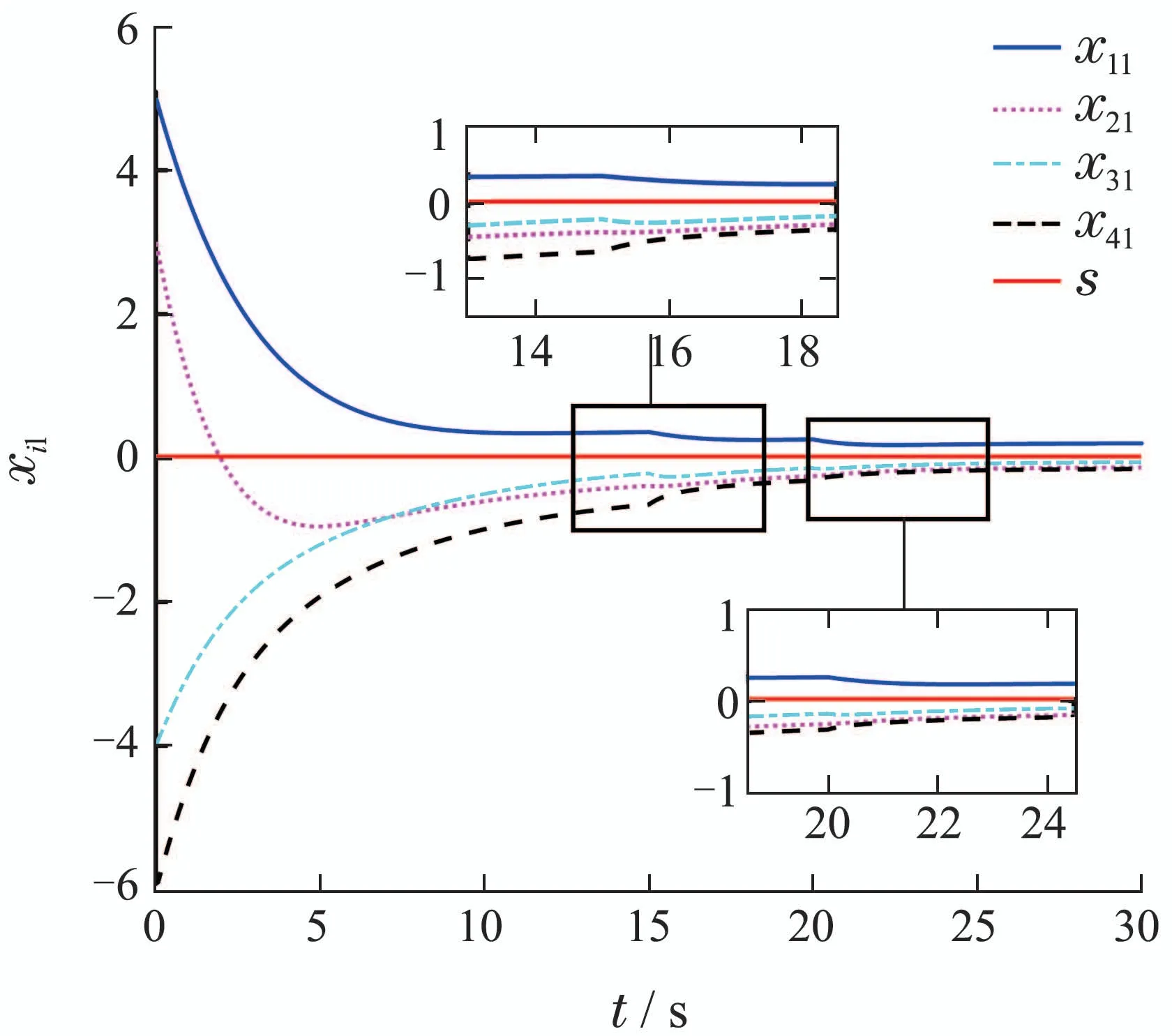
图2 系统状态轨迹xi1Fig.2 Trajectory of states xi1

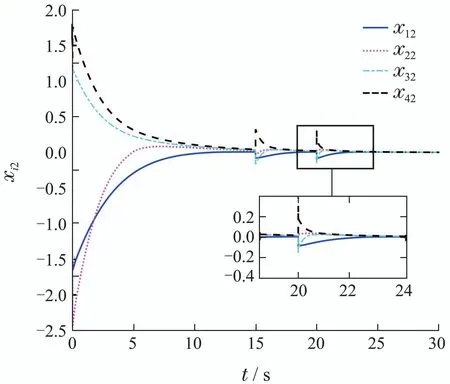
图3 系统状态轨迹xi2Fig.3 Trajectory of states xi2

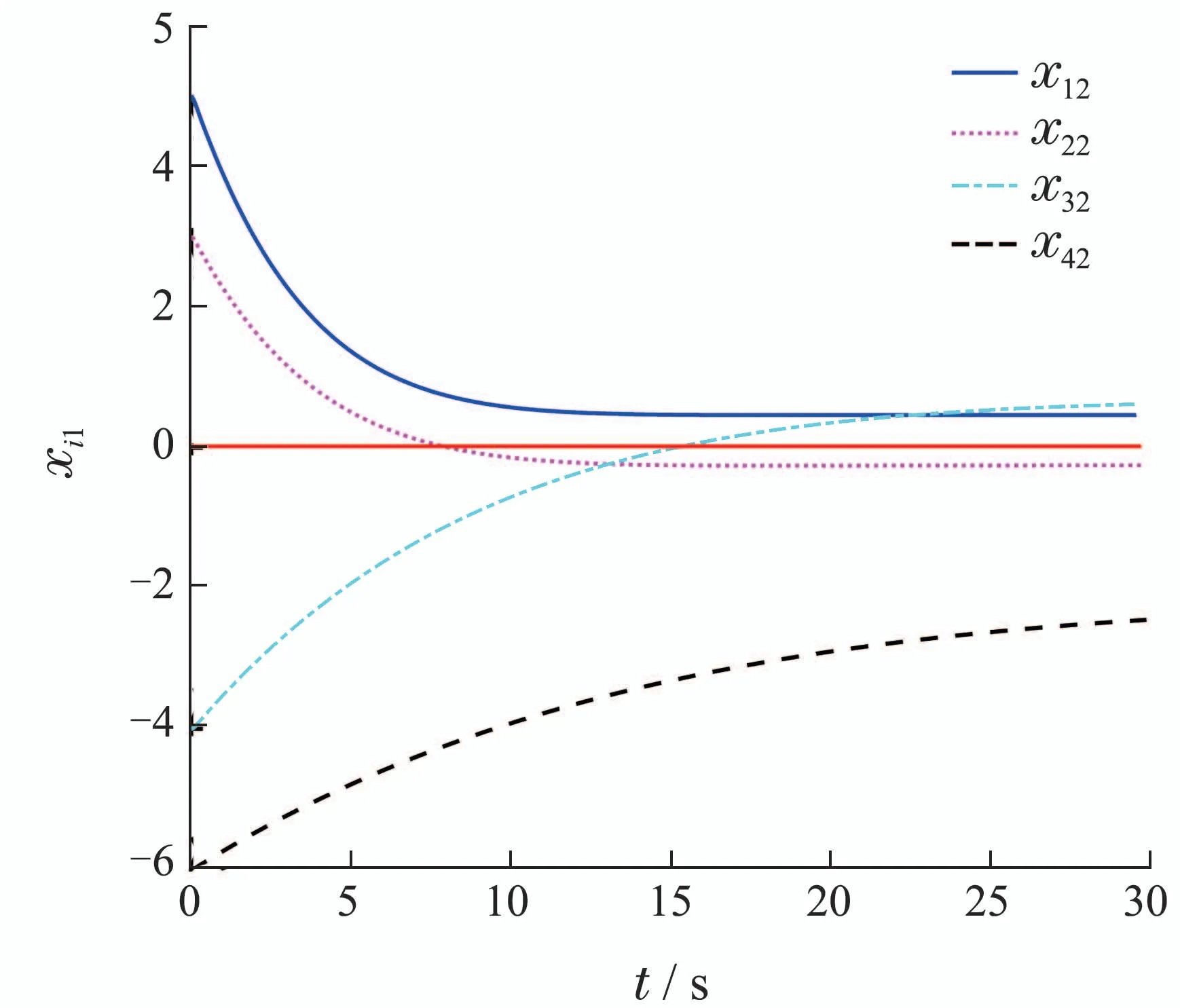
图4 传统算法Fig.4 Traditional algorithm

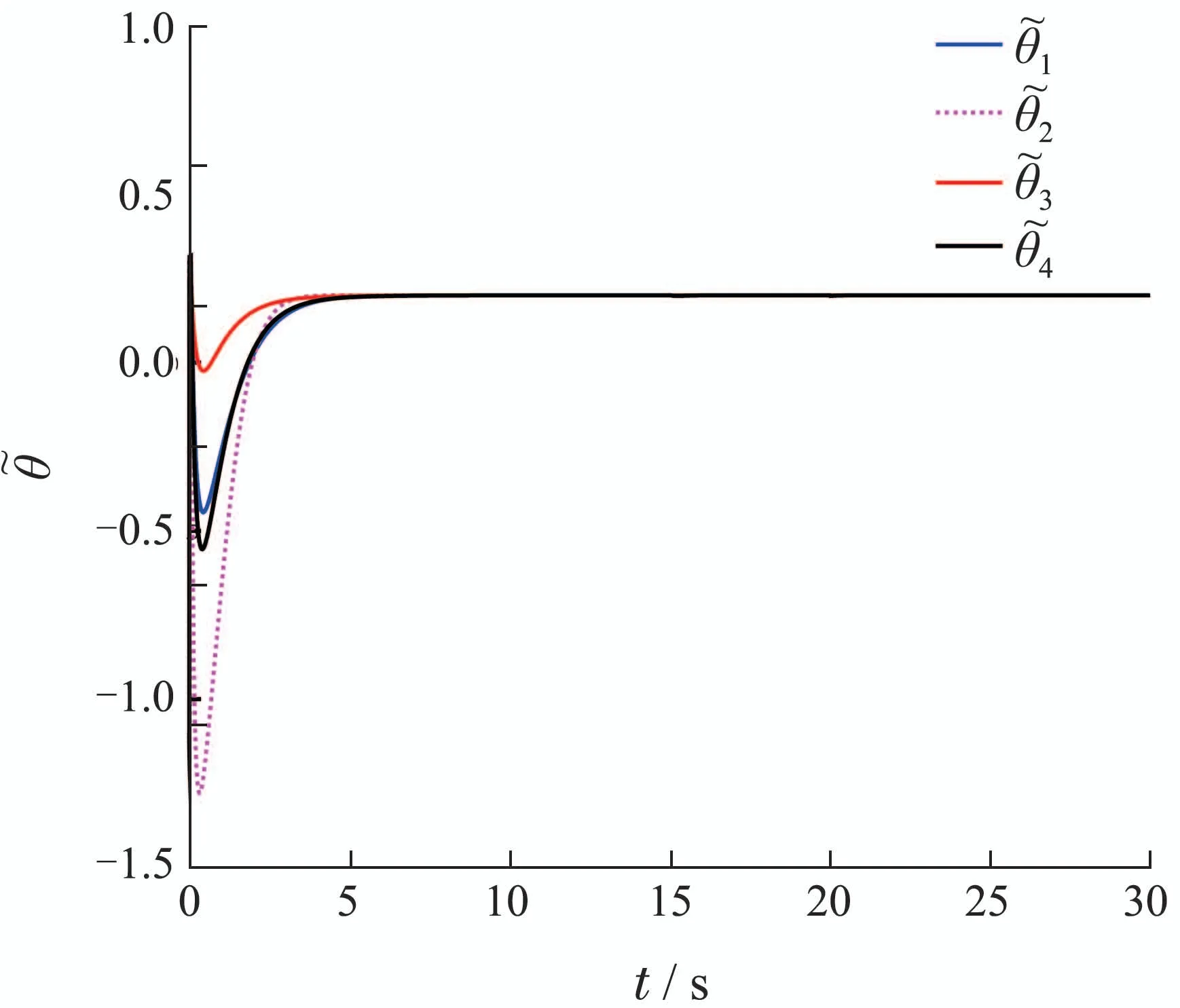
图5 自适应参数误差θ˜Fig.5 Trajectory of unknown parameter error θ˜

5 结论

本文在固定无向拓扑下,对一类二阶非线性多智能体系统的分布式优化问题进行了研究.将多智能体系统分布式优化问题,转化为带有等式约束的优化问题,并构造相应的惩罚函数,基于惩罚函数,结合幂积分技术和负梯度方法,设计了有限时间分布式控制协议,并通过调整惩罚项使得多智能体系统能够达到一致的最优解.最后,通过仿真验证了理论结果的有效性.