加筋混凝土梁抗剪承载力统一计算方法研究

2021-07-30 03:01屈文俊何松洋刘文博

铁道学报 2021年6期

屈文俊，何松洋，刘文博

(1.同济大学土木工程学院, 上海 200092；2.中国电力工程顾问集团西南电力设计院有限公司送电结构科，四川成都 610000；3.中国民航机场建设集团公司建筑所，陕西西安 710065)

加筋混凝土梁多为钢筋混凝土梁、FRP筋混凝土梁和FRP筋-钢筋混合配筋混凝土梁，依据其主拉应力图以及抗剪破坏现象，其抗剪加强筋的布置方式基本一致，即设置横向抗剪箍筋。从表面上看，其差异为不同抗剪筋力学性能的差异，可以尝试推荐统一的抗剪计算公式。根据混凝土构件的剪切破坏模式[1]，基于修正压力场理论(MCFT)[2-3]，利用材料间的应变协调和应力平衡关系，对加筋混凝土梁的抗剪承载力计算方法进行理论推导，建立加筋混凝土构件抗剪承载力模拟计算方法，参照已有的研究成果，试图提出一个便于工程应用的统一计算公式。

1 加筋混凝土梁抗剪破坏模式

加筋混凝土梁包括了钢筋混凝土梁、FRP筋混凝土梁和混合配筋混凝土梁，其剪切破坏模式总体上是相似的，具体破坏形态因为材料的差异存在一定的差别。

钢筋混凝土梁按照腹筋的布置形式可分为无腹筋梁和有腹筋梁。无腹筋梁的斜截面剪切破坏模式主要有三种形态[4]：斜拉破坏、剪压破坏和斜压破坏。不同规范的计算公式，都是建立在剪压破坏模式之上的。

FRP筋混凝土梁按照腹筋的布置形式也可分为无腹筋梁和有腹筋梁。无腹筋FRP筋混凝土梁剪切破坏模式与混凝土梁相似[5]。配置FRP箍筋混凝土梁的剪切破坏模式主要有两类[6]：一类为FRP箍筋断裂而引起的破坏，另一类为梁剪跨区加载点处混凝土剪压压碎而引起的破坏。FRP规范推荐的破坏模式与钢筋混凝土梁剪压破坏模式类似，以FRP箍筋应变达到应变极限和剪压区混凝土压碎作为破坏条件，据此建立了FRP箍筋混凝土梁的抗剪计算公式。

混合配筋梁的剪切破坏模式与钢筋混凝土梁类似[7]，包括了斜压、剪压和斜拉三种破坏模式。剪压破坏包括两种：①与传统钢筋混凝土梁的剪压破坏形态完全一致，破坏时钢筋纵筋未屈服，但钢箍筋已经屈服，称为剪压破坏模式；②最终发生斜截面剪切破坏时，钢箍筋屈服，且跨中纵向钢筋也发生了屈服，称为弯剪破坏模式。

综上，加筋混凝土梁的抗剪破坏模式大体可以分为斜压、剪压和斜拉三种，为了充分利用箍筋的强度，并使得破坏具有一定的延性，实际工程中希望梁发生剪压破坏，抗剪计算公式的推证是建立在剪压破坏模式之上的。为了统一考虑剪跨比的影响，对于钢筋混凝土梁和FRP筋混凝土梁，偏于安全地取λ>2.5为斜拉破坏的判别标准。

2 加筋混凝土梁抗剪承载力的理论计算

Mitchell等[8]提出了拉力场的计算理论，但是试验结果表明，混凝土开裂后斜裂缝之间仍存在不可忽略的拉应力。因此，Vecchio等[2]在压力场的基础上提出了修正压力场理论(MCFT)，MCFT通过裂缝间的平均拉应变来考虑裂缝间混凝土的拉应力，认为混凝土开裂后，剪力由拉、压应力共同承担。研究表明，修正压力场理论(MCFT)的计算结果与试验结果更加吻合，更被广泛地应用于各国规范中[9-12]。

本文拟在经典修正压力场理论(MCFT)的基础上[13]综合考虑钢筋混凝土梁、FRP筋混凝土梁和FRP筋-钢筋混凝土梁三种梁的配筋方式，以及钢筋单元、FRP筋单元和混凝土单元的相互关系，根据钢筋混凝土构件的剪切原理，并结合应力平衡条件和应变协调条件对加筋混凝土梁的抗剪承载能力进行计算分析。

2.1 应变协调条件

取开裂后加筋混凝土单元进行应变分析，分析单元见图1(a)。

由于不考虑筋材的滑移，则有

εbx=εcx=εx

(1)

εby=εcy=εy

(2)

式中：εbx、εby分别为钢筋或FRP筋在x、y方向的应变；εcx、εcy分别为混凝土在x、y方向上的应变；εx、εy分别为单元体在x、y方向上的应变。

单元的应变状态摩尔圆见图1(b)，由莫尔圆及几何关系有：

图1 应变协调条件

混凝土单元x方向的应变为

(3)

混凝土单元y方向的应变为

(4)

式中：εc1为混凝土主拉应变；εc2为混凝土主压应变；θ为混凝土斜裂缝夹角。

2.2 应力平衡条件

混凝土及筋材单元的应力状态见图2。由x方向的受力平衡为

图2 混凝土单元及筋材单元的应力状态

(5)

由于假定单元表面正应力和剪应力均匀分布，同时，不考虑配筋引起的混凝土面积减少，式(4)可以简化为

σx=σcx+ρsxσsx+ρfxσfx

(6)

同理由y方向的受力平衡为

σy=σcy+ρsyσsy+ρfyσfy

(7)

式中：σsx、σsy分别为钢筋在x、y方向的应力；σfx、σfy分别为FRP筋在x、y方向的应力；σcx、σcy分别为混凝土在x、y方向上的应力；τcxy为混凝土单元的剪切应力；σx、σy分别为单元体在x、y方向上的应力。ρsx、ρfx分别为钢筋、FRP筋在x方向配筋率；ρsx、ρfx分别为钢筋、FRP筋在x方向配筋率；τxy为单元体剪应力。

单元的应力摩尔圆见图3，根据摩尔圆几何关系为

图3 单元应力摩尔圆

σc2=σc1-τxy(tanθ+cotθ)

(8)

式中：σc1为混凝土主拉应力；σc2为混凝土主压应力。

2.2.1 横向平衡条件

纯剪状态下的梁单元平衡条件见图4。横向受力见图4(a)。

图4 纯剪状态下的梁单元平衡条件

y向平衡关系(不考虑应力正负符号，所有值绝对值化)为

(9)

假定截面上剪应力均匀分布，即

(10)

联立式(9)和式(10)得出统一抗剪承载力为

(11)

式中：Asv为钢箍筋面积；Afv为FRP箍筋面积；σsv为钢箍筋应力；σfv为FRP箍筋应力；bw为梁截面宽度；s为箍筋间距。式(11)即为修正压力场理论的抗剪承载力计算公式，但式(11)中σc1、σsv、σfv、θ为未知量。若取σc1=0.7ft(ft为混凝土抗拉强度)，σsv=fsv，Afv=0，θ=45°，式(11)即可化为我国混凝土设计规范中的均布荷载作用下的抗剪承载力计算公式。

2.2.2 竖向平衡条件

纯剪状态下的梁单元竖向受力如图4(b)所示。x向混凝土的合力(不考虑应力正负符号，所有值绝对值化)为

Nv=Vcotθ-σc1bwh0

(12)

2.3 混凝土及筋材本构关系

2.3.1 钢筋及FRP筋本构关系

根据工程设计的经验，钢筋采用理想弹塑性本构模型，FRP筋采用线弹性模型。

2.3.2 混凝土受压本构关系

混凝土受压本构关系采用文献[2]考虑受拉软化效应的本构模型为

(13)

(14)

式中：σc2max为混凝土峰值压应力；ε0为混凝土峰值压应力对应的应变。

2.3.3 混凝土受拉本构关系

当εc1≤εcr(εcr为混凝土开裂应变)时，混凝土开裂前，拉应力与拉应变呈线性关系，采用线弹性本构[2]为

σc1=Ecεc1

(15)

当εc1>εcr时，推荐采用如下本构关系[2]为

(16)

2.4 弯剪复合状态下的计算方法

2.4.1 纯弯状态

纯弯状态下的计算简图见图5，不考虑混凝土拉应力的影响，α1、β0为混凝土受压区等效图形系数。

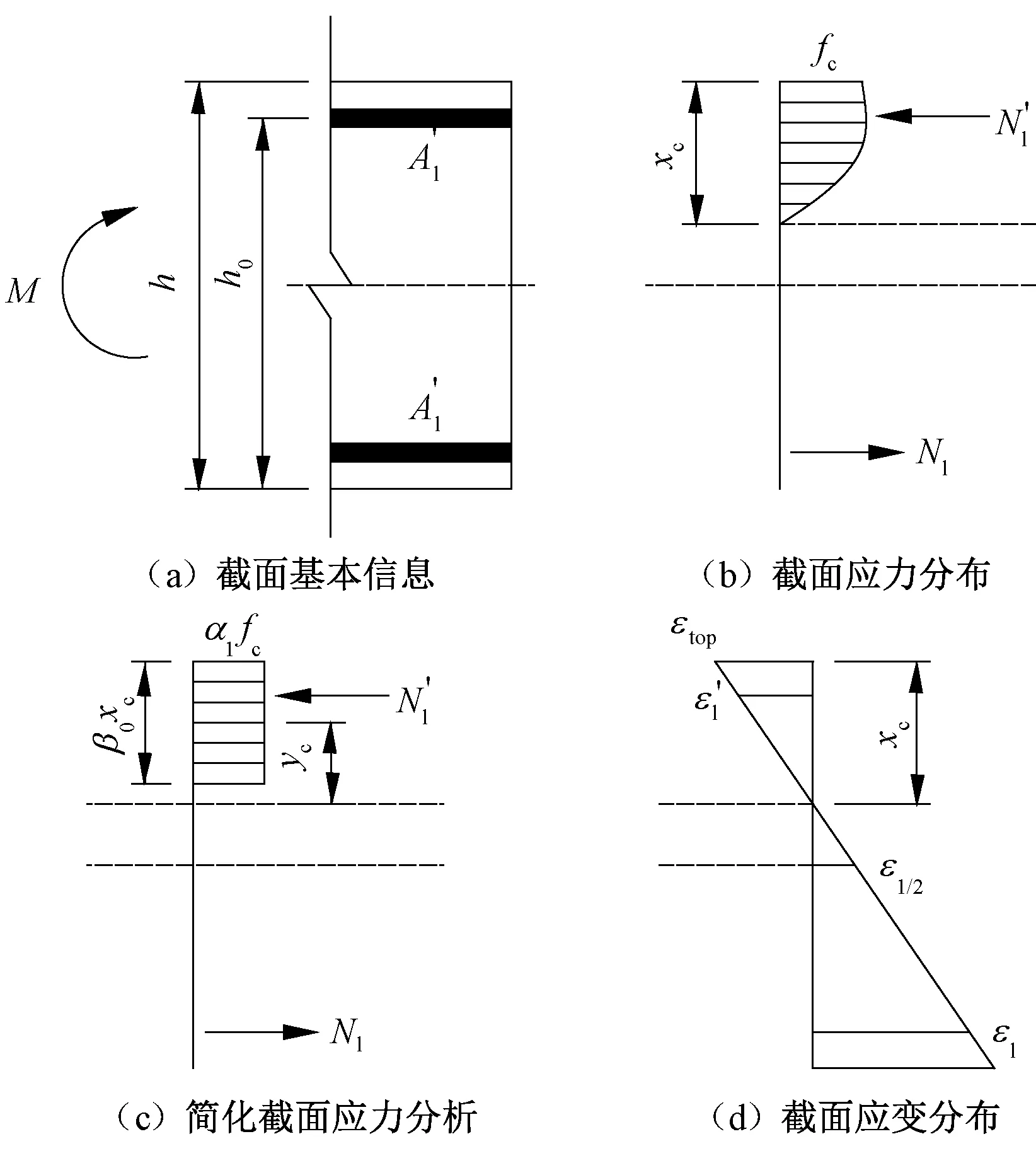
图5 纯弯状态下的截面计算简图

由图5的几何关系有

(17)

当εtop≤ε0时，混凝土受压区合力为

(18)

当εtop>ε0时，混凝土受压区合力为

(19)

受拉及受压筋内力为

(20)

(21)

此时，截面的弯矩为

M=Nc(h0-β0xc/2)+N′l(h0-a′s)

(22)

式中：xc为混凝土受压区高度；yc为等效图形的形心至截面中和轴的距离；εtop为梁顶混凝土受压应变(取绝对值)；h0为混凝土受压区有效高度；a′s为纵筋合力点到截面受压区边缘的距离；εl、ε′l分别为受拉、受压纵筋应变；ε1/2为截面0.5h高度处纵向应变；fc为混凝土抗压强度设计值；El为筋材的弹性模量；Al为受拉筋的面积；A′l为受压筋的面积。

2.4.2 弯剪复合状态

实际工程中，混凝土梁在受剪区域实际上是处于弯剪复合状态，附加的弯矩会增大截面的纵向应变，进而减小梁的抗剪承载力。在弯剪复合受力状态下，纯剪下假定的截面剪力均匀分布也会由于弯曲应力的影响而重分布，导致梁中混凝土单元的主应力方向会随着截面高度而变化，从而引起斜裂缝倾角θ沿梁高而不断变化，这使得分析难度大大增加。在实际分析时，为了便于计算，一般先假定斜裂缝倾角θ为定值，并根据1/2梁高处的纵向应变计算斜裂缝倾角θ。

文献[2]采用MCFT理论计算时，取纯剪状态下的纵向应变εx作为截面1/2高度处的应变，并据此计算其余各参数，本文通过与试验数据对比分析发现，采用截面1/2高度处的应变计算弯剪复合受力状态下的抗剪承载力时，大多数情况下是偏不保守的，即Collins[2]的取值方法高估了梁的抗剪承载力。这是因为梁在受弯时，截面受压区高度通常会小于0.5h，即截面0.5h高度处仍处于受拉状态，0.5h高度处的应变仍为拉应变，且弯曲产生的拉应变与剪切产生的纵向应变方向相同，叠加后0.5h高度处的应变会增大，所以在弯剪复合受力状态下，截面1/2高度处的实际纵向应变是大于εx的，而纵向应变越大，抗剪承载力就越小，此时仍采用εx作为截面1/2高度处的应变的初始值，就会使计算得到的抗剪承载力偏不保守。本文通过对搜集的试验数据进行统计分析，建议取弯曲内力臂为0.9h0时截面0.5h高度处的弯曲应变与剪切应变εx叠加作为弯剪复合状态下截面0.5h高度处的纵向总应变ε1/2，计算式为

ε1/2=εx+ε0.9h0

(23)

两种取值方法的计算结果见表1。

表1 ε1/2两种取值方法计算结果对比

由表1可知，ε1/2=εx时，AR几乎都小于1，偏于不保守，且保证率很低；而取ε1/2=εx+ε0.9h0时，AR值都大于且接近1，保证率相对较高，更符合实际。

2.5 抗剪承载力计算

弯剪复合状态下的计算流程见图6。

图6 加筋混凝土梁抗剪承载力计算流程

2.6 理论计算结果与试验结果的对比

为了验证理论计算方法的合理性，本文搜集了国内外学者关于钢筋混凝土梁、FRP筋混凝土梁及FRP筋-钢筋混合配筋混凝土梁的抗剪试验数据，试验梁的数量见表2。

表2 试验梁数据库

为了便于对比分析，本文选取国内外的钢筋混凝土梁设计规范[14-17]以及FRP筋混凝土梁设计规范[18-20]作为比较对象，理论计算结果与各国规范的抗剪承载力计算结果见表3。

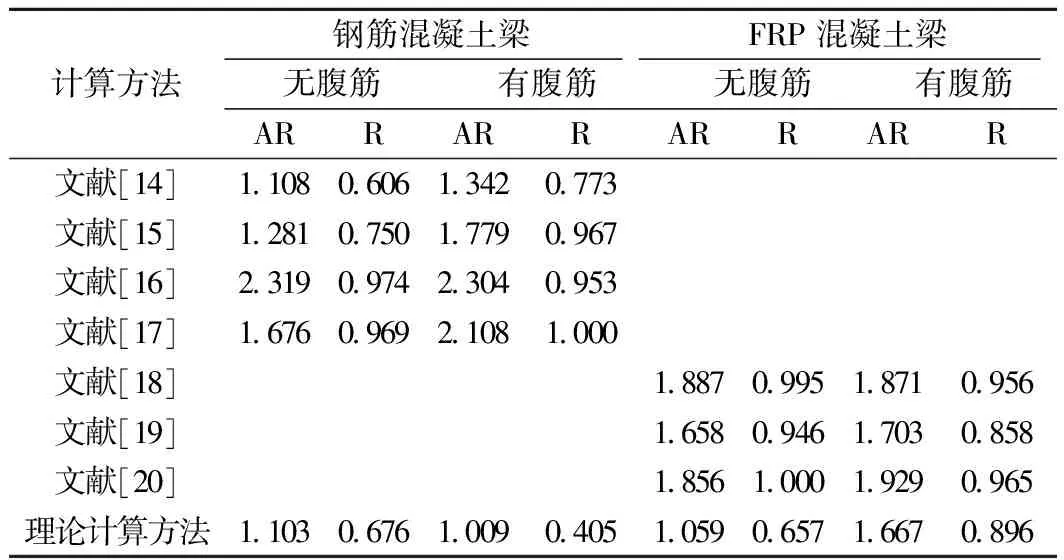
表3 理论计算结果与各国规范的计算结果

另外，由于国内外并没有计算FRP筋-钢筋混合配筋混凝土梁的抗剪承载力设计规范，所以单独列出混合配筋混凝土梁的计算结果，见表4。

表4 混合配筋混凝土梁抗剪承载力的计算结果

2.6.1 各国规范计算结果与试验结果的对比

钢筋混凝土梁的抗剪能力计算上，规范计算的AR位于1.108～2.319之间，均大于1，R位于0.606～1.0之间，均大于60%，且文献[14]的计算结果与试验结果最为接近。

FRP筋混凝土梁的抗剪能力计算上，规范计算的AR位于1.658～1.929之间，均大于1，R位于0.858～1.0之间，均大于85%，规范计算结果与试验结果偏差较大。

2.6.2 理论计算结果与实验结果的对比

钢筋混凝土梁的抗剪能力上，理论计算的AR位于1.009～1.103之间，均大于且接近1，说明理论计算结果与试验结果吻合较好。

FRP筋混凝土梁的抗剪能力计算上，无腹筋梁的AR为1.059，说明理论计算结果与试验结果吻合较好，有腹筋梁的AR为1.667，吻合相对较差，但仍然偏于安全。

混合配筋混凝土梁的抗剪能力计算上，理论计算的AR为1.029，说明理论计算结果与试验结果吻合较好。

对比结果说明，可以采用理论计算方法进行模拟实验，且文献[14]的计算结果与试验结果吻合较好。

3 计算公式形式的推荐

3.1 计算公式的确定

参照成熟的研究成果和标准规范，以剪压破坏模式为计算公式的模型基础。从剪压破坏形态来看，抗剪承载力极限状态下主裂缝宽度决定了箍筋的允许拉应力。允许拉应力与箍筋的弹性模量成正比，剪压破坏时，钢箍筋与FRP箍筋的应变大致相同，FRP箍筋的允许应变值参照文献[7]给的建议值，取为0.002。本文以修正压力场理论推出的抗剪承载力表达式(10)为基础，参照文献[5，14]给出的抗剪计算公式形式，推荐统一计算公式取为

(24)

式中：β1、β2和β3为待定参数；ss、sf分别为钢箍筋间距及FRP箍筋间距；bw为截面宽度，矩形梁取截面宽度，T或I型梁取腹板宽度；h0为截面有效高度；fc为混凝土抗压强度；fyv为钢箍筋的屈服强度；Efv为FRP箍筋的弹性模量；αλ为剪跨比影响系数，ρeff,l为纵筋等效配筋率[5]，计算式分别为

(25)

(26)

其中，Esl、Efl分别为钢纵筋和FRP纵筋的弹性模量；Asl、Afl分别为钢纵筋和FRP纵筋的截面面积。

为了确定β1、β2和β3三个参数，将通过本文提出的计算模型进行数值模拟实验，通过无腹筋钢筋混凝土梁的数值模拟实验来确定β1，在确定好参数β1的基础上，通过有腹筋钢筋混凝土梁的数值模拟实验来确定β2，然后通过有FRP腹筋混凝土梁的数值模拟实验来确定β3，参数确定的原则是保证每个数值试验计算结果的保证率达到90%以上，以此保证统一计算公式的可靠度满足设计要求。

数值模拟试验设计了2 176根简支混凝土梁，梁的跨度均为5 000 mm。为了便于分析，选取了两种截面尺寸：300 mm×400 mm和300 mm×600 mm，具体的参数变化见表5。当受拉纵筋为钢筋时，布置4根钢筋；当受拉纵筋为FRP筋时，布置5根FRP筋；箍筋采用双肢箍。其中，钢纵筋采用HRB400，屈服强度为fy=360 MPa，钢箍筋采用HPB300，屈服强度为fy=270 MPa；FRP纵筋弹性模量[7]104取为Ef=4.0×104N/mm2，FRP箍筋弹性模量[7]104取为Ef=5.0×104N/mm2。