牵引电力电子变压器次谐振现象机理及抑制策略

刘华东，张志学，陈 涛，黄子昊

(1.西南交通大学 电气工程学院，四川 成都 611756；2.中车株洲电力机车研究所有限公司，湖南 株洲 412001)

为了减小高速列车牵引主变压器的重量和体积，提高牵引系统的传输效率和灵活性，多种采用高频变压器HFT(High Frequency Transformer)的拓扑被学者提出[1-5]。这类拓扑的思路是把单相工频高压交流电经过电力电子变换器变为中高频交流电，经过高频变压器进行隔离和降压之后再与牵引逆变器相连。这种采用多电平整流器和高频隔离的新型变换器拓扑，被称为电力电子变压器(Power Electronic Transformer,PET)[6-7]，用于轨道交通牵引系统的电力电子变压器(Power Electronic Transformer for Traction，PETT)[8-11]。为了提高效率，PETT多采用级联整流器和LLC谐振变换器结合的拓扑[12]。

由于PETT采用单相整流拓扑结构，直流侧电压中将包含二倍频谐波电压[13-14]；在网侧级联整流器中，由于死区时间和直流侧电压二次脉动等原因，电流中将会产生大量的低次谐波，如3、5、7次等谐波，耦合至直流电压中，将产生大量偶次谐波，如4、6次等谐波电压[15-16]。同时，直流侧电压中还包含大量网侧级联整流器开关频率特征次谐波和LLC谐振变换器开关频率特征次谐波[17]。直流电压这种谐波特性将在网侧整流器和LLC谐振变换器中交叉耦合，直流侧电压中的低次谐波(如100，200 Hz等)和级联整流器开关频率特征次谐波都可能在LLC谐振变换器中发生次谐振现象，将直流侧电压中的低频谐波分量放大，严重影响LLC谐振变换器软开关实现范围，增加谐振变换器的电路损耗。目前尚无文献揭示这种现象的原理，也无文章针对此现象提出相应的系统参数优化设计方法和控制策略。

本文揭示直流侧二倍频等低次谐波电压在LLC谐振变换器中产生次谐振的机理，分析次谐振引起ZVS范围减小和电路损耗增加的原因，定量计算谐波电压放大系数与网侧功率、直流电容值、直流电压谐波次数和网侧谐波电流次数的关系。给出网侧开关频率、直流电容等系统参数的优化选取方法和低次谐波的抑制策略。试验验证了本文所推导数学模型和定量分析的正确性，所提方法和策略的有效性。

1 PETT拓扑结构

PETT主电路拓扑如图1所示，分为高压级联整流器、LLC谐振变换器、逆变器负载。

(1) 高压级联整流器

高压级联整流器由多个H桥单元串联而成，通过电感Ls接入25kV高压牵引网上。每一个H桥单元分别经过整流输出多个不同电位的分布式直流电压。级联整流器的主要功能是保持电网侧单位功率因数，输入电流为正弦波，维持分布式直流电压稳定和平衡。一般情况下，为了提高装置效率，单个H桥单元开关频率一般选为几百赫兹。

(2) LLC谐振变换器

LLC谐振变换器将高压级联整流器输出的多个不同电位的直流电压逆变为高频方波，再经过高频隔离变压器HFT耦合至副边，再整流为低压直流输出，完成电压转换和高低电位隔离。原次边变换器均采用H桥方式，能量可以根据牵引和制动工况实现双向流动。

为了提高牵引系统效率，LLC谐振变换器原边利用谐振元件实现全负载范围内的ZVS和小电流关断；次边实现零电流关断(Zero Current Switch，ZCS)。为了减小高频变压器体积和重量，电路谐振频率一般选为2 kHz以上。如果开关器件允许，一般认为谐振频率越高越好。

由图1可知，级联整流器中间直流侧电容均连接单相H桥整流器和LLC谐振变换器，中间直流侧电压将含有2倍频等低次谐波电压，同时，还包含整流器和谐振变换器的开关特征次谐波。

2 LLC谐振变换器次谐振现象

2.1 次谐振机理

LLC谐振变换器的拓扑如图2所示，本文以能量正向流动为例进行描述。Udc为图1中级联整流器某个H桥的输出直流电压，Lr、Lm分别为高频变压器Tr的漏感和励磁电感，Cr为谐振电容，ir为谐振电流，Uo为输出直流电压。

图2 LLC谐振变换器示意图

由上述可知，直流电压Udc中包含不同频率的谐波电压，可以表示为

(1)

式中：Udc0为直流分量；Udck为k次谐波电压幅值；ω为工频电压角频率；ψk为k次谐波电压初始相位。

根据LLC谐振变换器的原理，输入电压Udc经过Q1、Q2、Q3、Q4逆变成50%占空比的方波电压输出，开关频率为fs。这可以等效为一个频率为fs、幅值为1的正负方波信号S(ωst)对Udc进行采样，从而得到Uab。

Uab=S(ωst)×Udc

(2)

其中

(3)

对周期函数式(3)进行傅里叶分解，可得

(4)

将式(1)、式(4)代入式(2)，可得

k=1,2,…,N;n=1,3,5,…，M

(5)

由于n≥3时，电压幅值很小，且LC谐振回路在n≥3频率段的阻抗非常大，所以不考虑n≥3时电压所产生的电流，只考虑n=1时的情况，则有

(6)

进一步对式(6)计算，可得

(7)

如果对式(7)进一步做三角运算可知，谐振电路的输入电压激励Uab不仅含有ωs分量，还含有(ωs±kω)分量(又称为“差频”分量)。当k值较小时，这些频率分量的阻抗非常接近，在LC谐振时，阻抗都接近为0，特别是差频分量(ωs±2ω)(由直流电压中的2次分量产生)，含量丰富且频率接近谐振。所以，LLC谐振变换器电流中将含有大量由低次谐波电压产生的谐波分量，类似于电机控制时的“拍频”现象[18]。这些分量电流的叠加会使谐振电流异常波动，影响LLC谐振变换器ZVS实现的范围，并产生额外的损耗。

2.2 次谐振现象对ZVS范围影响分析

由上述可知，LLC谐振变换器电流中含有多频率段的谐波分量，这些分量谐波电流的叠加会使谐振电流异常波动。在谐振电流波动至幅值较大时(见图3红框内区域)，方波电压将会产生震荡，导致当IGBT开通时，就不再是ZVS，增加开关损耗，降低IGBT器件的安全性。下面分析谐振电流波动大时，导致ZVS失败的原因。

图3 次谐振现象波形

如图4所示，LLC谐振变换器的关断电流为Iturn-off，开关器件(图2中Q1～Q4)死区时间为Td，结电容(图2中C1～C4)放电时间为Tc，二极管(图2中D1～D4)续流时间为ΔTφ。

图4 ZVS范围影响

由文献[12]可知，要完成原边ZVS过程，死区时间Td应该满足

Tc≤Td≤Tc+ΔTφ

(8)

当Td>Tc+ΔTφ，即续流时间小于死区时间时，方波电压将产生震荡，也不满足ZVS。如图4所示，在t1时刻，Q1、Q4关断，关断电流为Iturn-off，关断后，结电容C2和C3放电，C1和C4充电。C2、C3放电完成后，二极管D2和D3开始续流，Q2和Q3两端电压为零，为零电压开通准备了条件，当Q2、Q3的驱动脉冲在D2、D3续流时间段内有效，则Q2、Q3完成零电压开通。如果在电流到零时，死区过程仍未结束，Q2、Q3仍然没有驱动脉冲，则C1、C2、C3、C4之间开始充放电，Q2、Q3两端电压不再为零，甚至随着结电容的充放电出现震荡。当Q2和Q3的驱动脉冲达到时，就不再是零电压开通。

由文献[19]进一步推导出二极管续流时间ΔTφ的简化计算式为

(9)

式中：Ipeak为电流幅值；ωr为电路角频率；Iturn-off为LLC谐振变换器关断电流。由文献[14]可知，当LLC谐振变换器的电路参数、输入电压和开关频率确定后，ωr和Iturn-off保持不变。因此，ΔTφ与Ipeak成反比，当电流幅值越大时，二极管续流时间越短，也就是说ZVS越容易失败。

因此，在谐振电流波动时，为了保证实现全负载范围的ZVS，一般情况下，就需要提高关断电流或减小死区时间。这样将会增加IGBT关断损耗，增加安全风险。

2.3 次谐振现象对电路损耗影响分析

如果在LLC谐振变换器电流波动时，仍能保持全负载范围的ZVS和ZCS，则LLC谐振变换器的开关损耗保持不变，通态损耗由于谐波分量的增加而增大。下面将定量分析LLC谐振变换器通态损耗与谐波分量的关系。

IGBT在开通时，可等效成一个电阻Rj。电路中电能损耗计算使用的电流为均方根电流值[20]。当电流中含有谐波时，电流的波形会发生畸变。根据定义，畸变波形下谐振电流的均方根值为

(10)

式中：I1为LLC谐振变换器的基频ωs电流；I2,I3,…，Ih为其他频率段的谐波电流。

在计算时段T内，基频电流在IGBT等效电阻Rj上产生的通态损耗PLoss-1为

(11)

假设在k次谐波下IGBT等效电阻仍为Rj，则k次谐波电流在IGBT上产生的通态损耗PLoss_k为

(12)

所以，IGBT的通态谐波总损耗为

(13)

从以上分析可以看出，由于LLC谐振变换器中其他频次的谐波分量增加，会使谐振电流的有效值增加，从而引起附加的通态损耗，降低LLC谐振变换器的效率。为了对次谐振现象引起的电路附加损耗进行定量分析，假设电流谐波总含量THDr为

(14)

由于

(15)

所以

(16)

从式(16)可以看出，由次谐振产生的额外通态损耗等于谐振电流的总谐波含量的平方，即如果次谐振现象产生30%的总谐波，则LLC谐振变换器通态损耗增加9%。

3 谐波电压放大定量分析

3.1 低次谐波电压数学模型

单相系统中，直流电压中存在二次电压脉动，究其原因是由于交流侧功率和直流侧功率不平衡造成的。通常情况下，都是以瞬时功率平衡的思路，来分析直流侧电压存在二次电压脉动和其他低次偶数谐波电压的原因。单相PWM整流器等效电路如图5所示。

图5 单相PWM整流器等效电路

如图5所示，假设网侧电压为理想电压，瞬时值为us，基波有效值为UN，电流瞬时值为is，基波有效值为I1N，k次谐波有效值为IkN，ω为工频角频率，直流侧电压为Udc，Udc中直流分量为Udc0，二倍频电压幅值为Udc2，负载为RL1，直流侧支撑电容为C1，忽略其他高次谐波及连接电感上的压降，只考虑电流中的奇次谐波，结合文献[15-16]，可以得到二倍频电压幅值Udc2为

(17)

由式(17)可知，二倍频电压幅值与输入功率成正比，与电容值近似成反比。由文献[16-19]可知，当PWM整流器网侧电流中含有3、5、7次等谐波时，PWM整流器直流侧含有4、6、8次电压脉动Udc4、Udc6、Udc8。定量推导过程与2次电压类似，可近似表示为

(18)

(19)

(20)

实际上，由于网侧整流器和LLC谐振变换器的开关作用，在直流电压中，还存在一定的2fc(fc为网侧整流器开关频率)和2fs(fs为LLC谐振变换器开关频率)的高次谐波。一般情况下，如果fc与fs相差很大时，2fc谐波也可能会在LLC谐振变换器中产生次谐振现象。由于其定量推导非常复杂，本文不做详细推导。

3.2 谐波电压放大系数定量分析

仍以直流电压中的2倍频分量为例进行计算，如图2所示，假设LLC谐振变换器电路增益为M，高频变压器变比为N，开关次特征谐波电压幅值为Udcn，初始相位角为σn，则输出电压Uo可表示为

(21)

输出电容Co的电流ic为

(22)

由式(22)计算可得

(23)

负载电流可以表示为

(24)

由于电容的高频吸收作用，负载电流中的高频电流可忽略，那么有

(25)

由于

iD=ic+iL

(26)

将式(23)和式(25)代入式(26)可得

(27)

由于LLC谐振变换器次边二极管整流导通和关断的时序与原边IGBT的时序完全一致，因此，在i2经过二极管整流后，同样等效于一个频率为fs、幅值为1的正负方波信号对iD进行采样，从而得到i2。

同上可得

i2=s(ωst)×iD

(28)

将式(4)代入式(28)可得

(29)

如果只考虑n=1时的情况，则有

(30)

进一步做三角运算可知，i2中主要含有3种频率分量，分别为ωs、(ωs-2ω)、(ωs+2ω)。这3种频率分量的电流瞬时值表达式为

(31)

sin[(ωs-2ω)t+α1]

(32)

sin[(ωs+2ω)t+α2]

(33)

由图2可知

(34)

其中

n=1,3,5,…，N

(35)

由式(35)可知，励磁电流im中也含有差频分量。但由于励磁回路阻抗较大，通过计算得到im中含有的ωs、(ωs±2ω)差频分量远小于i2中的差频分量。所以，在原边谐振电流的差频分量主要由式(32)和式(33)决定。2、4、6次谐波电压也有类似的结果。

4 LLC次谐振抑制方法

4.1 系统参数的优化选取

(36)

(37)

同理，对式(17)进行近似计算，可得

(38)

将式(38)代入式(36)和式(37)可得

(39)

(40)

由式(39)和式(40)可知，当额定功率等系统参数确定后，差频电流的幅值主要是由LLC谐振变换器的输出电容和PWM整流器直流电容的比值决定，而且近似成正比例关系。与中间直流电压Udc成反比关系。2、4、6次谐波电压产生的差频电流也有类似的结果。

4.2 直流侧电压偶次脉动抑制

直流侧电压中除了存在2次脉动外，还会因为电网侧电流的3、5、7等低次谐波，使得直流电压中存在4、6、8等偶次电压脉动。一般来说，2次电压脉动在不加额外电路的情况下，很难消除，但如果加入辅助电路，又与PETT轻量化的目标相违背[10-14]。因此，本文的目标是允许2次脉动的存在，通过一定的控制策略来抑制电网侧低次谐波，尽量消除直流电压中4、6、8等偶次电压脉动，从而消除偶次电压谐波引起的次谐振现象。本文抑制电网侧低次谐波的思路是在级联整流器控制器中加入可以抑制对应次数的谐波控制器。图1中级联整流器可等效为图5中的单相H桥整流器，谐波控制器通过提取总电流is中的某次谐波分量，再通过PI调节器控制该次谐波分量为零。谐波控制器与重复控制有类似的频率特性，即可以在特定的频率处产生无穷大的增益，从而可以对这些频率处的谐波电流实现无静差跟踪或者对这些频率处的扰动产生全抑制作用。

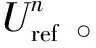
图6 谐波控制器原理

5 试验验证

5.1 样机概况

为了验证文中PETT的功能，制造出一套25 kV/1 800 kV·A的PETT样机。PETT电网侧采用级联整流器，DC/DC变换器采用LLC谐振变换器，直流侧输出电压1 800 V给牵引逆变器供电。全功率样机参数见表1，样机如图7所示。

表1 全功率样机参数

图7 样机实物

如图7所示，样机系统主要由充电电路、高压模块(高压级联整流器)、高频变压器、低压模块和控制器组成。其中，高频变压器的主要作用为隔离高低电位，原边为高压模块，副边为低压模块。

5.2 参数优化选取试验验证

根据4.1节参数优化选取的计算和推导，改变C0/C1的比值和中间直流电压Udc的大小，验证参数优化选取的原则和经验。

图8(a)中，Co为4 mF，C1为2 mF；图8(b)中，Co为1 mF，C1为2 mF。因此，当Co/C1的比值由2变至0.5时，谐振电流的波动明显减小。

图8 谐振电流波形

图9(a)中，中间直流电压为3 600 V，交流侧输入功率为200 kW。图9(b)中，中间直流电压降至1 800 V，保持输入功率不变，则谐振电流波动增大，同时直流电压的波动增大。

图9 不同直流电压的谐波电流波形

在实际设计过程中，在综合考虑LLC谐振变换器软开关的范围、功率器件的耐压等级、装置整体效率、系统动态响应速度、二次电压允许波动范围和装置体积的基础上，尽可能的提高直流侧电压，减小电容C0，适当增大整流侧电容C1，减小差频分量。

5.3 直流侧电压偶次脉动抑制验证

由于在轻载时，网侧低次电流谐波含量最大，直流侧中偶次谐波含量(主要指4、6、8次谐波)也最大。本文在最恶劣的工况下测试低次谐波对直流电压及谐振电流的影响。

图10为轻载时测试波形，网侧电流小于10 A，中间直流电压额定值2 200 V。图10(a)为未采用谐波控制器时网侧含有大量的低次谐波电流，直流侧电压含有100、200、300 Hz等偶次谐波。图10(b)为采用谐波控制器后，网侧电流中低次谐波被消除，直流侧电压仅仅含有100 Hz的2倍频电压。

图10 轻载时测试波形

图11为轻载时级联整流器电压、整流器电流、直流电压和LLC谐振回路电流。由图11可知，采用谐波控制器后，网侧电流正弦度比未采用谐波控制器时的正弦度好，谐振电流的波动也更小。

图11 谐振电流效果对比

由此可见，通过抑制电网侧低次谐波，能够降低直流侧耦次谐波的含量。同时，也能够减弱LLC谐振变换器的次谐振现象，减小谐振电流的波动。但此控制策略无法消除直流电压中2次脉动对LLC谐振变换器的影响。

6 结论

PETT直流侧电压中的低次谐波电压引起LLC谐振变换器中产生次谐振现象。本文在分析次谐振产生机理后，得到以下结论：

(1)LLC谐振变换器电流中会由于次谐振现象，产生大量的差频谐波分量。这些分量电流的叠加将会使谐振电流异常波动，影响LLC谐振变换器ZVS实现的范围。所以，在设计LLC谐振变换器关断电流时，为了保证全负载范围内的ZVS，需要考虑差频谐波分量的影响。

(2)差频分量的存在，还会使开关管产生额外的通态损耗。在分析LLC谐振变换器的散热条件和效率时，需将额外的通态损耗计算在内。通态损耗增加的百分比为谐振电流总谐波含量的平方。

(3)通过定量分析可知，减小LLC谐振变换器的差频分量，可以通过提高直流侧电压、减小输出电容和中间电容的比例、消除网侧电流低次谐波等方法实现。但是，差频分量的产生是由于直流电压中含有2倍频等偶次谐波电压，由于PETT的单相拓扑结构，在不设计2次滤波支路的情况下，2倍频电压始终存在。因此，LLC谐振变换器差频分量只能抑制部分，无法彻底消除。