基于深度学习的城轨列车轴承复合故障诊断研究

姚德臣，刘恒畅，杨建伟，李 熙，崔晓飞

(1.北京建筑大学 机电与车辆工程学院， 北京 100044；2.北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室， 北京 100044；3.北京市地铁运营有限公司， 北京 100044)

随着城市轨道交通运营里程的迅速增加，运送客流规模急剧增大，城轨列车作为城市轨道运输的载体，如何在快速运行条件下保障城轨列车的运行安全已经成为各城市共同面临的严峻考验。以某地铁统计数据为例，在轨道车辆走行部故障中机械部件故障高达78%，轴承是最易损坏的零部件之一[1]。

列车轴承最常见故障模式为局部损伤或缺陷，缺陷部位通过其他接触元件表面时会产生冲击振动[2]。因列车运行环境的特殊性，极易导致轴承复合故障发生。列车轴承复合故障发生时，其振动信号往往是非线性非平稳的，且包含有多种频率成分，而且在其运行过程中，这些频率成分的幅值和频率又会受到周期性冲击力的调制。因此，列车轴承复合故障振动信号是一种非线性非平稳的多分量调幅-调频信号[3]。传统滚动轴承故障诊断方法通常包括以下步骤：

(1)原始振动信号的数据预处理。

(2)振动信号特征提取。

(3)使用指定的模型进行故障分类[4]。

特征提取是为了提取信号中有用的故障信息，从而提高故障诊断的准确率[5]。常用的特征提取方法包括短时傅里叶变换(STFT)、小波变换、主成分分析法等。就目前国内外常用于故障特征提取的各种信号处理方法来说，虽然都具有一定的效果，但在针对非平稳、非线性信号的适用性方面以及方法本身的理论方面，仍存在着不同程度的局限性。

目前多数故障诊断方法在面对非平稳、非线性信号时需要人工选择特征，不同的特征选择决定了故障诊断的效果；另一方面现有特征提取方法随着数据量的增大，算法性能会逐渐降低。为克服上述诊断方法缺点，深度学习理论被引入到故障诊断领域。深度学习来源于机器学习，目前被广泛应用于图像检测、图像分类、自然语言处理等领域，被称为未来走向人工智能的途径之一。与传统浅层模型相比，深度学习避免了对诊断经验和特征提取的需求，同时能够满足在“大数据”时代，对故障诊断准确率的高要求[6]。

CNN最初被作为一个深度学习架构提出，可以直接使用图片像素矩阵作为输入，避免了繁琐的特征提取。CNN模型具有三大特点：权值共享，局部连接，降采样[7]。局部连接意味着每个神经元结点只需要接收局部的像素点作为输入，不用像传统的多层感知机(MLP)每一个神经元都要接收图片的全部像素点信息。权值共享则意味着同一卷积层中每一个过滤器的权重是一样的，因此卷积层的参数量只和卷积核的尺寸大小有关。降采样来自于池化层，减少了输出参数量，使模型具有对输入数据平移的容忍性，提高了模型的泛化能力。CNN模型解决了传统神经网络在层数加深后计算复杂度大、过拟合的问题，大幅提高了模型的泛化能力。

CNN模型已广泛应用于故障诊断领域。文献[8]提出基于卷积神经网络的滚动轴承故障诊断，利用CNN模型成功对美国凯斯西储大学公开的轴承故障数据进行分类。文献[9]于1998年提出了手写字体识别的LeNet-5模型，由于其较强的泛化能力，至今仍在很多领域被改进应用。文献[10]提出短时傅里叶变换和LeNet-5模型结合分析轴承故障。文献[11]提出卷积神经网络和小波时频图相结合的滚动轴承故障诊断。上述方法都能有效诊断轴承外圈、内圈和滚动体故障，但较难辨识轴承复合故障。

本文采用一维振动信号转二维图像的思想，利用CNN模型特征挖掘能力，免去了故障诊断中筛选特征环节，提高了故障诊断效率，为改进轴承故障诊断路线提供了新思路。

1 理论分析

1.1 技术路线

本文提出的基于深度学习的城轨列车轴承复合故障诊断方法，利用CNN模型图像分类的功能对轴承复合故障进行诊断。首先需要将采集到的一维振动信号进行标准化，并转换为二维数组，将数组以图形方式保存作为特征样本，分为训练集和测试集；在Le-Net5模型的基础上建立深度学习模型；将训练集作为模型的输入，对模型进行训练，获取适合城轨列车轴承故障诊断的最佳网络架构和参数；最后将测试集输入到训练好的模型中，对模型效果进行评估。故障诊断方法流程见图1。

图1 诊断方法流程

1.2 图像生成

原始振动数据为一维时间序列信号，而CNN模型的输入数据要求是二维矩阵。为了将一维时间序列转换成二维数据矩阵[12]，实验基于固定取样间隔R，每次取样M个采集点为一个行向量li，将li进行归一化。对于取N个行向量所构成的M×N矩阵P，为一个图像样本。实验中R取1 024，M、N取64。li归一化公式为

P=[l1l2…ln]T

(1)

(2)

式中：x*为归一化前的值；xmax为最大值；xmin为最小值。

振动信号生成图像样本见图2，经过伪彩色处理后的故障图像样本见图3。

图2 振动信号生成图像样本

图3 振动信号故障图像样本

1.3 深度学习

深度学习模型一般由输入层、卷积层、池化层(降采样层)、全连接层和输出层组成。

输入层是整个深度学习模型的输入，一般会对输入数据进行数据预处理，比如去噪、数据归一化等，在本实验中，输入层的数据即灰度图的像素矩阵。

卷积层是卷积神经网络能够发挥其优势最重要的层次，与传统的全连接神经网络不同，卷积层中每一个节点的输入都是上一层中的一小块，因此卷积神经网络具有稀疏交互的特点，而这一特征通过“卷积核”实现[13]。卷积核也称过滤器，卷积核用来提取输入数据中最基本的特征，卷积核的数量越多，卷积层能够提取的图片有效高阶特征也就越多。每一个卷积核的输出被称为特征映射(Feature Map)，卷积核的尺寸决定了特征映射的尺寸，卷积核的深度决定了下一层节点矩阵的深度。卷积神经网络具有权值共享的特性，即每一个隐含节点的参数都是一样的，所以卷积层的参数数量与卷积核的尺寸和深度有关，相对于传统全连接神经网络，卷积神经网络的参数个数减少了几个数量级。卷积操作计算过程见图4。

图4 卷积操作

构建卷积层时，需要设置图像填充方式和卷积步长。图片每次进行卷积运算后，输出图片的尺寸都会变小，在边缘像素点的信息也可能丢失。为避免上述问题，提出对图像使用全0填充，在输出的节点矩阵边界位置补充0使得输出节点矩阵和输入节点矩阵的尺寸相同。卷积步长表示卷积核每次在进行卷积运算时，其在图片上的步进长度[14]。例如一个输入图片尺寸为n×n、卷积核尺寸为f×f、全零填充的值为p、卷积步长为s的卷积层输出矩阵尺寸为

(3)

卷积层后通常会接池化层，池化层可通过缩小矩阵的尺寸进一步减少模型的参数数量，池化层通过一个与卷积核类似的结构完成运算，与卷积核区别在于，池化层通过计算矩阵区域中的最大值或者平均值达到缩小矩阵尺寸的目的，计算最大值方法的池化层被称为最大池化层，计算平均值方法的池化层被称为平均池化层。目前较常应用的为最大池化层。池化层使得CNN具有对图像缩放、旋转和平移的不变性[15]。最大池化层的计算过程见图5。

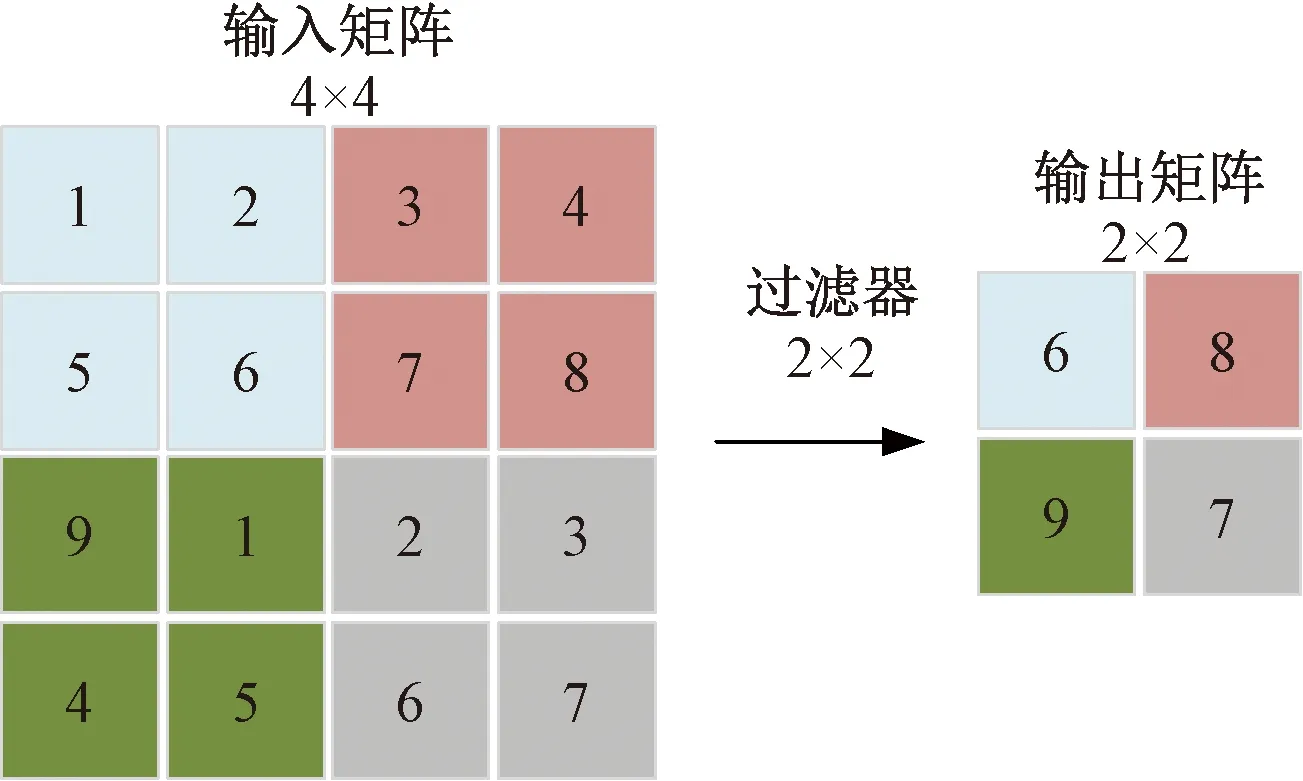
图5 最大池化操作

2 实验验证

2.1 构建数据集

为了验证本文所提算法的有效性，设计轴承故障试验台。试验台由驱动电机、联轴器、齿轮箱和磁粉制动器等组成，齿轮箱按城轨列车齿轮箱传动比定制。在试验台整个运行过程中，采集振动加速度信号，采样频率为12 kHz，转速为1 200 r/min，包含5种轴承状态：正常、内圈故障、外圈故障、滚动体故障以及复合故障。实验用的轴承型号为NJ202ECP。部分状态轴承见图6，外圈故障轴承由于外圈无法拆卸，所以没有拍摄故障图片。

图6 轴承运行状态

实验在Tensorflow的框架下开发，使用AMD的R5-2600x CPU(主频3.6GHz)，WIN10 64位操作系统，NVIDIA GTX1060显卡，主机上安装了 CUDA 9.0，Cudnn7.3对显卡运算进行加速。

每类故障中随机抽取500个样本，组成一个具有2 500个样本的训练集，再从剩余的数据集中分别从每种状态随机抽取100个样本建立一个具有 500个样本的测试集。

由于多分类CNN模型的输出为一个概率分布，所以要求输入标签必须是概率分布的形式，从而能够计算出模型输出与输入标签之间的交叉熵，根据交叉熵对网络进行优化。为解决上述问题，数据集中的样本全部使用独热编码(one-hot)制作标签，one-hot编码即将数字转化为一个只有一位是1，其余均为0的向量。使用one-hot编码的标签见表1。

表1 标签编码

实验算法基于Tensorflow开源深度学习框架进行设计，本实验采用数据集通过Tensorflow提供的统一存储格式TFRecord进行存储。

2.2 深度学习模型

在Le-Net5模型基础上建立适用于轴承故障诊断的深度学习模型，原始Le-Net5模型共有7层，包括3个卷积层、2个池化层和2个全连接层。原始Le-Net5模型见图7。

图7 原始Le-Net5模型

采用原始Le-Net5模型对轴承状态进行辨识，存在训练时间长、泛化能力差、分类效果不理想的问题。

为提高模型的收敛速度和精度，分别对模型的训练迭代次数、卷积核的尺寸、学习率、层数和优化器的选择等进行了实验。常用的卷积核尺寸有1×1，3×3，5×5。经多次验证，将卷积核尺寸定为5×5，卷积步长和池化步长均设为1。卷积操作和池化操作均使用全零填充，池化层使用最大池化方法。

原始的Le-Net5使用梯度下降法(Gradient)对模型参数进行优化，出现了训练时模型无法收敛的情况，即使加大训练迭代次数损失函数loss依然较大。因此在实验中将优化器替换成Adam优化器，Adam是一种自适应参数更新算法，可以在训练过程中改变学习率的值，根据梯度的一阶矩估计和二阶矩估计提供自适应性学习率。Adam优化器的详细流程见表2。β1、β2为指数衰减率，α为初始学习率，ε为常数避免除数为0的情况。

表2 Adam优化器的详细流程

为防止模型出现过拟合问题，提高模型的准确率，使用Dropout和L2正则化进行过拟合优化。为提高模型的泛化能力，Dropout通过在训练模型时，随机将指定比例的神经元节点的权值一般失活比例选为50%，本次实验中也设定为50%。

L2正则化通过权重衰减的方式，限制模型的学习能力，防止过拟合问题的出现。L2正则化的衰减公式为

(4)

式中：L为加上权重衰减后的损失函数；J为初始损失函数；λ为正则化惩罚参数；w为权重参数。

2.3 诊断结果

对模型中优化器种类和过拟合优化的使用进行多次实验，不同模型在训练集和测试集上的实验效果见表3。批尺寸(batch size)设为100，训练迭代次数设为4 000，学习率设为0.001，模型的网络连接方式为C1-P1-C2-P2-FC1-FC2。C代表卷积层；P代表池化层；FC代表全连接层。模型的网络结构见图8。

表3 不同模型实验效果

图8 模型网络结构

图9、图10分别为模型在使用不同优化器和过拟合优化时，loss值的优化效果以及训练时精度的变化。由图9、图10可以看出，Adam优化器相对于Gradient优化器可以加快模型收敛的速度，提高对loss值和训练精度的优化效果。

图9 不同优化器对loss的优化

图10 不同优化器训练集的精度

通过t-SNE算法可对模型在测试集上的预测进行降维和可视化，使输出的多维预测数据展现在2维空间上。t-SNE算法详细过程见表4[16]。表3不同模型在测试集上的数据分布见图11。

图11 不同模型的测试集数据分布

表4 t-SNE算法详细过程

为评测不同模型对每个状态的分类精度，对不同模型诊断结果使用混淆矩阵进行可视化，矩阵最右列代表输出类的精度，最后一行代表召回率。表3不同模型在测试集上的混淆矩阵见图12。

图12 不同模型的混淆矩阵

从实验结果可以确定最佳CNN模型。模型在训练时使用Adam优化器和过拟合优化时，可有效辨识列车轴承的复合故障。

3 结论

本文针对传统故障诊断方法，需要进行特征提取、依赖专家知识等缺点，提出基于深度学习的城轨列车轴承复合故障诊断方法，将其应用在列车轴承复合故障诊断中。通过实验，得到如下结论：

(1) CNN模型能够实现端对端的诊断模式，省去了传统诊断方法中复杂的特征工程。只需向模型输入转换后的图形，即可输出诊断结果。

(2) 通过使用Adam优化器对模型参数进行优化，能够加快损失函数收敛速度，提高模型的训练效率。

(3) 通过在训练中使用L2正则化和Dropout进行过拟合优化，能够有效提高模型的泛化性。最终模型在测试集上可以准确识别列车轴承的复合故障。

实验结果表明本文提出的基于深度学习的轴承故障诊断方法能较好地辨识城轨列车轴承复合故障。