需求和回收不确定的闭环供应链渠道结构选择

张 盟，郭健全

（1.上海理工大学管理学院，上海 200093；2.上海理工大学上海-汉堡国际工程学院，上海 200093）

0 引言

随着资源浪费和环境污染日益严重，可持续发展受到广泛关注［1］。回收再制造作为闭环供应链的重要部分，能够延长废旧品的使用寿命，缓解环境污染，降低生产成本，所以企业越来越重视回收再制造［2］。然而，闭环供应链系统更加复杂：如在不确定环境下，企业如何选择最优渠道结构并制定最优生产决策等，使闭环供应链面临诸多挑战［3］。

再制造闭环供应链面临更多不确定因素，市场需求、回收率、回收质量和再制造成本等主要不确定因素增加了企业在回收、生产和销售等决策上的难度［4］。市场需求的变化极大地影响企业的生产决策，不确定回收质量同时影响着回收率和再制造成本，因此需求和回收质量是重要的不确定因素［4］。Kim 等［5］考虑需求不确定建立了非线性规划模型；Ma 等［6］研究了需求不确定对价格的影响；Xiong 等［7］基于回收质量不确定研究了动态定价对总利润的影响；Heydari 等［8］在回收质量不确定下建立收益共享机制来分担不确定风险。上述文献单独讨论了整体需求和回收质量不确定性，然而现实市场需求往往划分为新产品和再制造品［9］，且经常同时出现需求和回收质量不确定，基于此，本文同时探讨不确定需求（新产品和再制造品需求）和回收品质量对最优决策的影响。

针对求解不确定问题的方法，Farrokh 等［10］采用随机规划法处理需求和成本不确定问题；Kim等［5］运用鲁棒优化解决需求不确定问题；Tsao 等［11］运用模糊机会约束规划法解决需求不确定问题。随机规划需要足够多的统计数据支持［10］；鲁棒优化过于注重置信水平，导致结果较为保守［5］；模糊机会约束规划法既可以解决缺少精确数值的问题，又能够避免结果过于保守［11］。因此，本文采用模糊机会约束规划法解决新产品和再制造品需求不确定问题。

政府补贴对回收再制造活动具有激励作用。Wang 等［12］研究了补贴制造商对经济效益和回收数量的影响；Sun 等［13］基于补贴制造商建立了进化博弈论模型；Li 等［14］探讨了政府消费补贴对社会福利和环境效应的影响；Bian 等［15］对比研究了补贴消费者和制造商对碳减排的影响。上述文献单独讨论了补贴制造商或消费者，未考虑回收质量对补贴额的影响，本文将回收质量考虑到政府补贴中，研究政府对制造商和消费者的差别权重补贴对最优决策的影响。

针对销售渠道选择问题，Li 等［16］采用直销渠道并研究了设计投资对均衡决策的影响；Xie等［17］基于双渠道销售研究了分级回收对缓解低质量回收的影响；Alamdar等［18］在零售商分销模式下考虑销售努力建立了六种博弈论模型；Xie等［19］研究了双渠道环境下闭环供应链的契约协调。上述文献只涉及单一销售渠道结构，直销和分销在不同情况下各有优劣，直销节省了产品库存成本，但是随着直销平台费用的增加，相较于分销显示出劣势，分销节省了直销平台费用，但是随着产品库存成本的增加，相较于直销显示出劣势［20］。因此，本文建立了四种销售渠道结构系统总利润模型，研究了不同情况下销售渠道结构的最优选择问题。

综上所述，本文以闭环供应链系统总利润最大化为目标，在市场需求和回收品质量水平不确定环境下考虑政府差别权重补贴和直销平台费用，构建了四种销售渠道结构闭环供应链系统总利润模型。运用模糊机会约束规划法解决新产品和再制造品需求不确定问题，并采用粒子群优化（Particle Swarm Optimization，PSO）算法和遗传算法（Genetic Algorithm，GA）对比求解模型算例。本研究可为企业在不确定环境下制定最优回收、生产和销售策略提供参考，同时为企业在不确定环境下选择最优销售渠道结构提供借鉴。

1 模型构建

1.1 模型假设

1）在一个周期中原材料只采购一次［21］；

2）不考虑提前期、缺货或过剩［22］；

3）单位再制造品利润大于单位新产品利润［22］；

4）回收品质量水平服从指数分布［3］；

5）政府实行差别权重补贴政策，消费者补贴权重为w，制造商补贴权重为1-w，0 ＜w＜1［23］。

1.2 符号说明

本文参数和决策变量的符号说明如表1和表2所示。

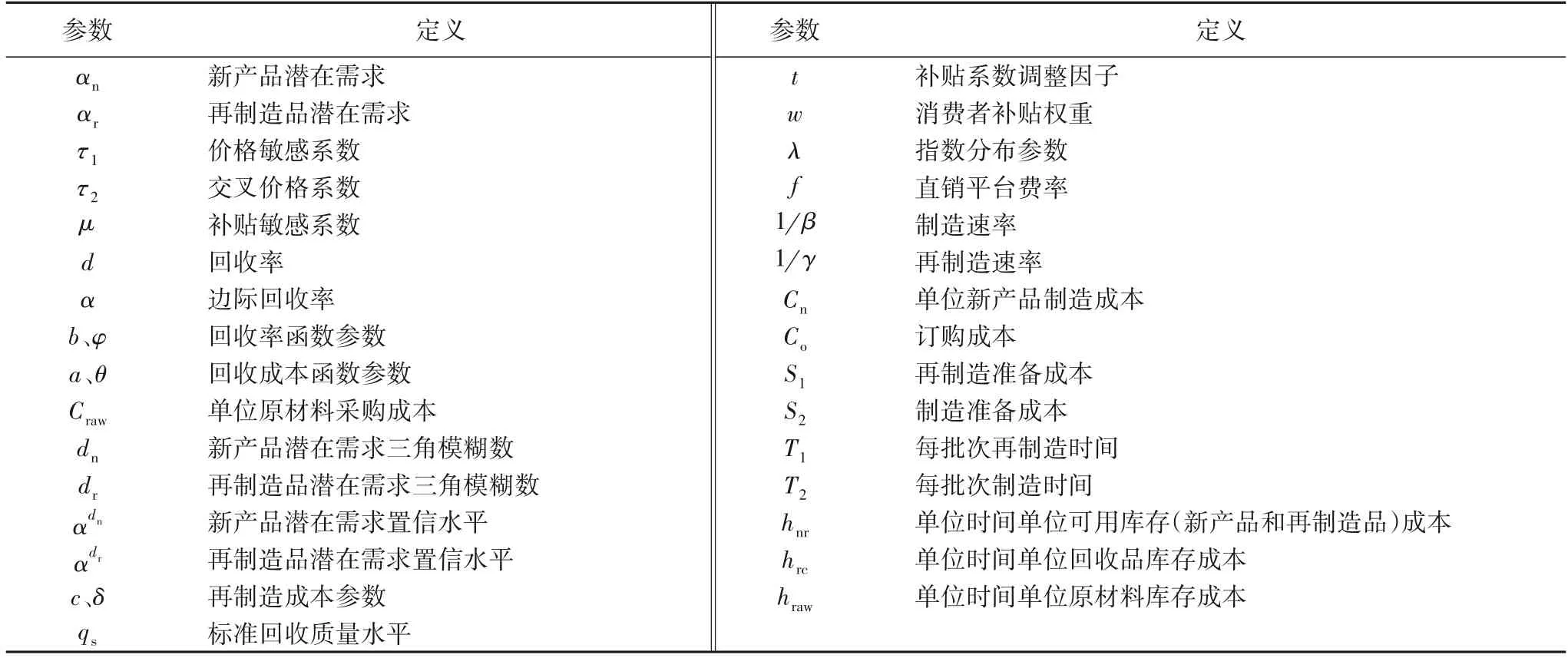
表1 参数符号说明Tab.1 Symbol description of parameters

表2 决策变量符号说明Tab.2 Symbol description of decision variables

1.3 函数构建

整体市场需求D包含新产品市场需求Dn和再制造品市场需求，函数为：

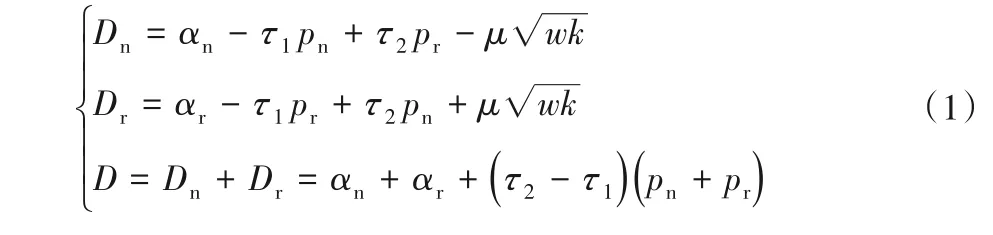
定义回收率d=αD，边际回收率α=be-φq［1］（0 ≤q≤1，0 ≤b≤1）。q为回收品质量水平，且服从指数分布q～E(λ)，λ为指数分布参数，q的概率密度函数为：

1.3.1 回收成本函数

定义回收成本比率p=ae-θ(1-x)［2］，a和θ为回收成本参数，0 ≤a≤1，p是单位回收成本与单位生产成本的比值。平均回收成本V1=d.Cn+Craw)E(p)，计算可得：

1.3.2 再制造成本函数

定义再制造成本比率j=ceδ()1-x［3］，c和δ为再制造成本参数，0 ≤c≤1，j是单位再制造成本与单位制造成本的比值，平均再制造成本V2=dCnE(j)，计算可得：

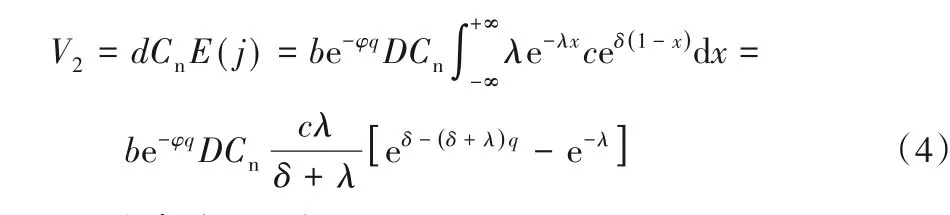
1.3.3 政府补贴函数

政府对制造商和消费者采取差别权重补贴政策。根据Guo 等［24］的研究，针对不同回收质量水平，单位再制造品补贴为k=则制造商总补贴额为：

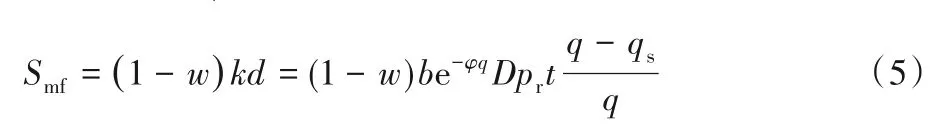
消费者购买再制造品的总补贴额为：

1.4 系统模型

制造商采购原材料用于新产品生产并回收废旧品用于再制造活动，新产品和再制造品通过直销或分销渠道进行销售，消费者从直销/分销渠道购买新产品或再制造品，并将废旧品回收给制造商，政府对制造商和购买再制造品的消费者进行补贴，如图1所示，整个过程形成物料循环流动。

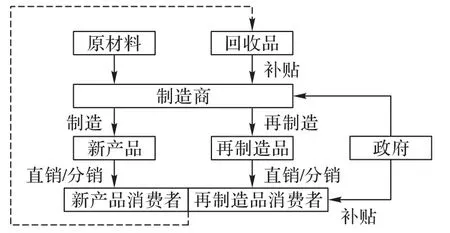
图1 闭环供应链系统模型Fig.1 Closed-loop supply chain system model

四种渠道结构如表3所示：第1种渠道结构采用直销渠道销售两种产品；第2 种渠道结构采用直销渠道销售新产品并采用分销渠道销售再制造品；第3 种渠道结构采用分销渠道销售新产品并采用直销渠道销售再制造品；第4 种渠道结道结构采用分销渠道销售两种产品。

表3 四种不同渠道结构Tab.3 Four different channel structures

1.4.1 库存水平

一个周期T包含l个制造期T2和m个再制造期T1，可得mDT1=dT，lDT2=DT-dT。库存状况如图2 所示，再制造品和新产品库存上升速度为回收品和原材料库存下降速度为

图2 库存状况（以m=2，n=2为例）Fig.2 Inventory status（with m=2，n=2 for example）

经过推导可得最大再制造品库存Ir、最大新产品库存In、最大回收品库存Irc和最大原材料库存Iraw为：

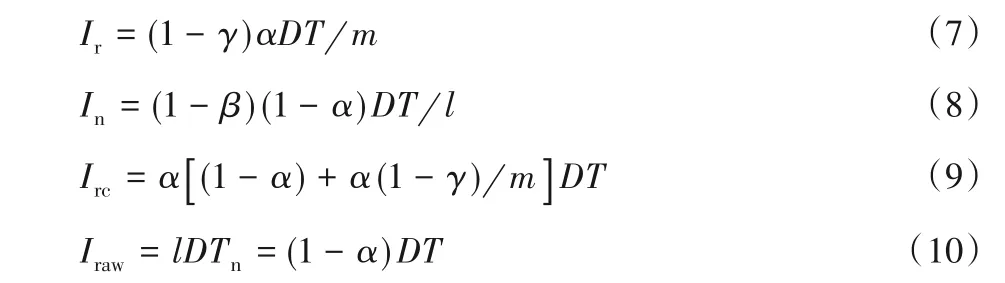
1.4.2 平均库存持有成本

再制造品和新产品平均库存持有成本为Hr和Hn、回收品和原材料平均库存持有成本为Hrc和Hraw，计算可得：

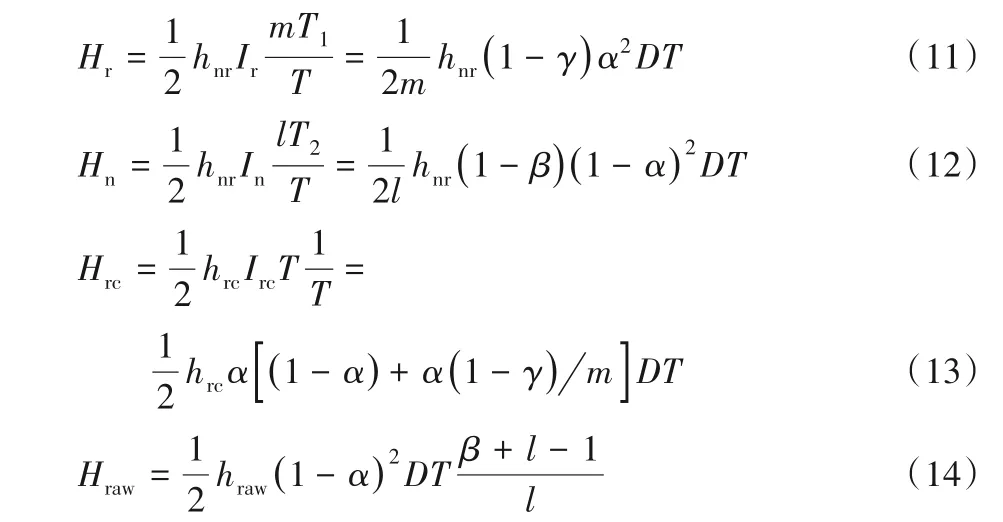
1.4.3 平均总利润

制造成本指新产品生产成本；订购成本指补充库存成本；原材料持有成本指维护原材料的成本；生产准备成本包括制造和再制造准备成本。平均制造成本V3、平均订购成本V4、平均原材料持有成本V5、平均生产准备成本V6计算可得：

直销和分销各有优劣，通过构建四种渠道结构系统平均总利润模型，研究不同情况下销售渠道结构的最优选择问题。

模型一 新产品和再制造品均采用直销渠道NSRS：

模型二 新产品采用直销，再制造品采用分销NSRL：

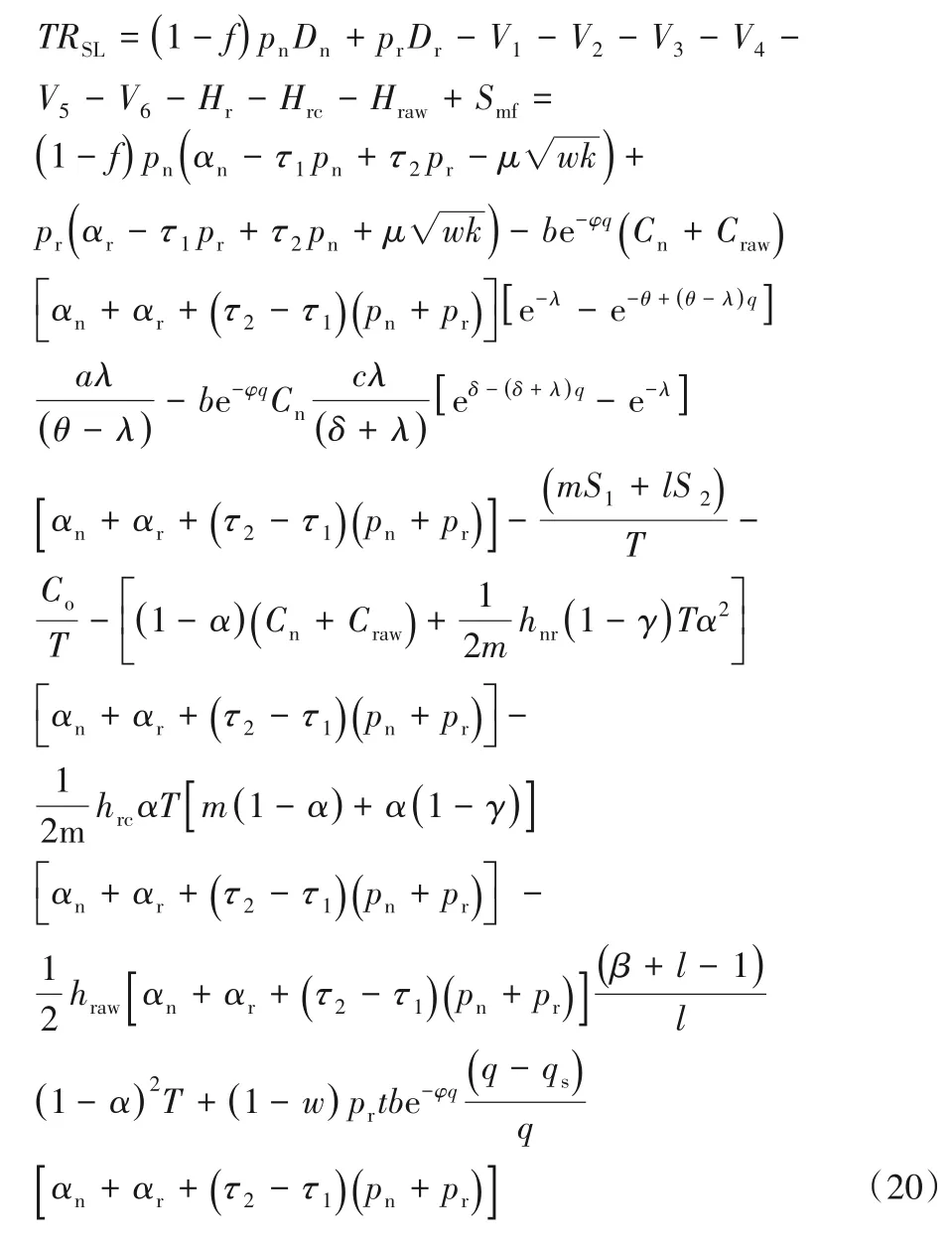
模型三 新产品采用分销，再制造品采用直销NLRS：

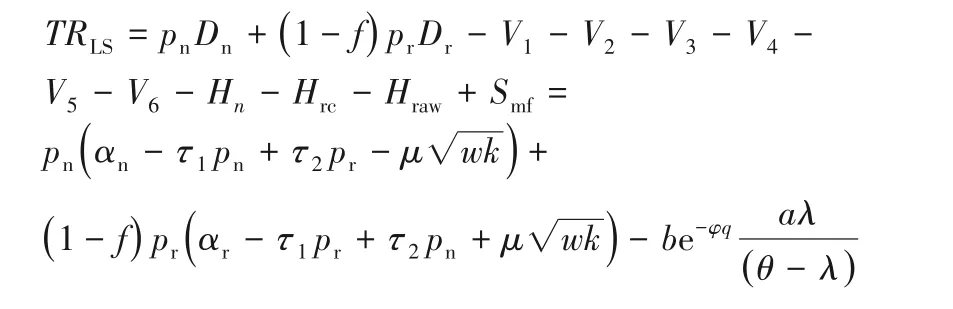
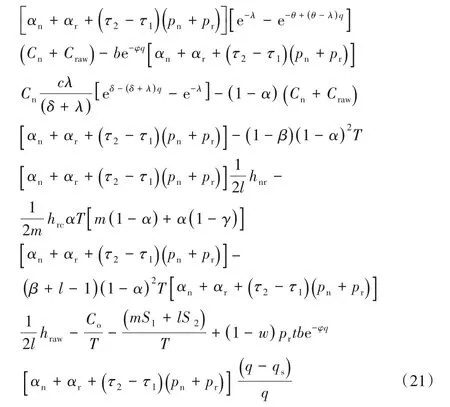
模型四 新产品和再制造品均采用分销渠道NLRL：

1.4.4 模糊机会约束清晰化

模糊机会约束规划（Fuzzy Chance Constrained Programming，FCCP）法的主要思想是将模糊约束转化为与之等价的确定式［11］。定义新产品和再制造品潜在需求模糊数为dn=(dn1，dn2，dn3)和dr=(dr1，dr2，dr3)，模糊隶属函数为：

由模糊机会约束规划法的清晰化定义及其引理可得：

其中：Pos{·}表示{·}中事件成立的可能性。

2 算法设计

传统优化方法求解具有连续/整数混合变量和不确定约束的非线性离散优化问题需要大量计算时间，元启发式算法被认为是有效解决方式［24］，例如GA、PSO 算法、蚁群优化（Ant Clony Optimization，ACO）算 法、禁忌搜索（Tabu Search，TS）等。

已知研究大多采用GA 和/或PSO 算法获得函数优化、选址与路径规划等问题的近似最优解，其中王心月等［3］验证了GA 与PSO 算法求解非线性离散优化问题时可以获得高质量解，Guo 等［24］采用PSO 算法与GA 对比求解函数优化问题，Soleimani等［25］通过GA与PSO算法验证了相关模型的信度。

PSO 算法和GA 均是用于搜索近似最优解的元启发式智能优化算法［26］，二者各有优劣：PSO 算法实现快，但易陷入局部最优；GA 能够同时处理多个种群个体，降低陷入局部最优的风险，但效率相对较低［27］。

本文主要研究闭环供应链管理问题，对比使用PSO 算法和GA 是为了求得高质量的近似最优解，进一步验证模型信度与算法效度。两者迭代过程具有互补优势，且相关研究采用两种算法对比验证了此类模型的信度，计算结果较好，其他如ACO 算法和人工蜂群（Artificial Bee Colony，ABC）算法等可能也可以解决该问题，在以后的研究中可以考虑。

2.1 粒子群优化算法

PSO 算法源于鸟群觅食行为的智能优化算法，在初始阶段生成一批随机解，通过不断迭代寻找最优解［26］。因其操作简单和易实现等特点，而被广泛应用于物流网络构建、路径规划等问题［28］。具体操作步骤如下：

1）随机初始化粒子位置、速度和各项参数：本文粒子群规模为30，最大迭代次数为200，搜索空间维数为6。

2）根据适应度函数获得粒子的适应度值：本文适应度函数为式（19）～（22）。

(4)环网柜处还需设置电压互感器，根据安装地电气条件和安装要求，选择电压互感器型号为JDZ9-10Q，高压侧电压为10 kV，低压侧电压100 V。绝缘性能优良、耐潮湿。

3）评估适应度值：根据历史和当前适应度值，找出粒子当前最优位置pbest和整个粒子群最优位置gbest。

粒子i的第d维速度和位置更新公式为：

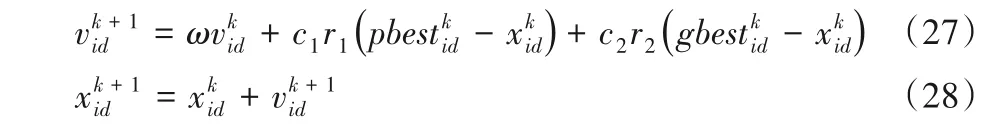
其中：c1和c2为加速常数；r1和r2为随机数，取值范围为［0，1］；ω是惯性权重。本文ω取0.729 8，c1=c2=2。

5）若达到终止条件（最大迭代次数），输出最优解，否则返回步骤2）。

图3 PSO的迭代收敛曲线Fig.3 Iterative convergence curve of PSO

2.2 遗传算法

GA 是基于遗传机制和自然选择的智能优化算法，通过复制、交叉和变异使群体不断进化，直到获得最优解［27］。因其具有并行性、全局寻优能力、自动调整搜索方向等特点，被广泛应用于物流网络构建、车辆路径规划、函数优化等问题［29］。具体操作步骤如下：

1）染色体编码与初始化。一条染色体对应问题的一个解，一个基因对应解的组成元素。本文染色体基因数为6，最大迭代次数为200，群体规模为40，交叉和变异概率为0.7 和0.03。本文采用二进制编码，随机产生0/1 初始种群，如表4所示。

表4 GA的初始种群Tab.4 Initial population of GA

2）计算适应度值。根据适应度函数f(x)=计算适应度值，object分别为式（19）～（22）。

3）个体选择。采用赌轮盘法进行个体选择，目标函数值越大，染色体越容易被选上，被选择的概率为：

4）交叉和变异。交叉变异过程如表5 所示，依据交叉和变异概率，随机产生交叉和变异位置。

表5 GA的交叉、变异操作过程Tab.5 Cross and mutation process ofGA

5）若达到终止条件（最大迭代次数），输出最优解，否则返回步骤2）。

3 算例分析

根据制造行业实际情况和相关文献［1-2，24］研究，设置参数值：hnr=2，hrc=0.2，hraw=0.2，Cn=30，Craw=20，Co=1000，S1=1500，S2=1500，a=0.9，b=0.9，c=0.1，γ=0.6，β=0.5，φ=2，λ=1，τ1=3，τ2=2，qs=0.2，μ=80，t=0.9，w=0.4，f=0.3。本文采用数据集进行模拟运算，潜在需求三角模糊数如表6所示。

表6 潜在需求三角模糊数Tab.6 Potential demand triangle fuzzy numbers

3.1 不确定环境下的最优决策

表7 采用GA求解不同置信水平下的最优决策Tab.7 Optimal decision at different confidence levels by using GA

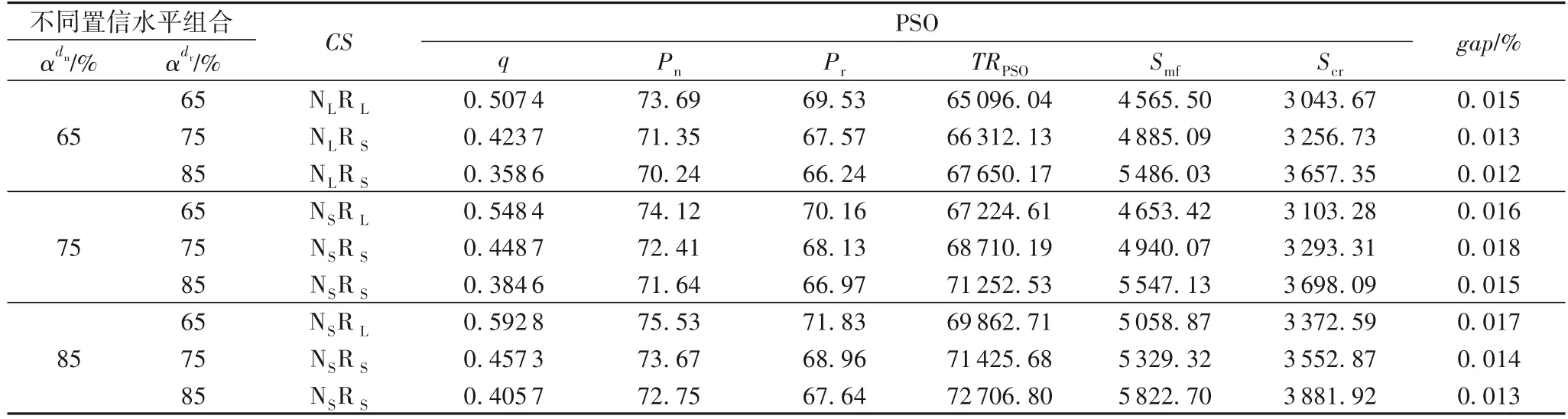
表8 采用PSO求解不同置信水平下的最优决策Tab.8 Optimal decision at different confidence levels by using PSO

管理启示：①随着再制造品潜在需求置信水平的增加，企业应生产较多的再制造品，通过增加政府补贴额来提高总利润；②随着新产品潜在需求置信水平的增加，企业应生产较多的新产品，通过降低采购运营成本来提高总利润；③企业可以根据新产品和再制造品潜在需求置信水平的不同组合制定最优回收、生产和销售决策，逐渐提高总利润。

3.2 不确定环境下的最优渠道结构选择

在新产品和再制造品需求不确定环境下，为进一步可视化分析销售渠道结构的最优选择问题，本文将销售渠道结构数值量化为：第1 至第4 种渠道结构分别赋值1、2、3、4，销售渠道数值量化为：直销渠道赋值10，分销渠道赋值20。

管理启示：①不确定新产品和再制造品需求会影响最优销售渠道结构选择，企业可以结合不同潜在需求置信水平，对销售渠道进行调整；②随着新产品和再制造品潜在需求置信水平的增加，企业应将新产品和再制造品从分销渠道逐渐调整为直销渠道；③企业可以根据不同潜在需求置信水平组合选择最优销售渠道结构，逐渐提高总利润。

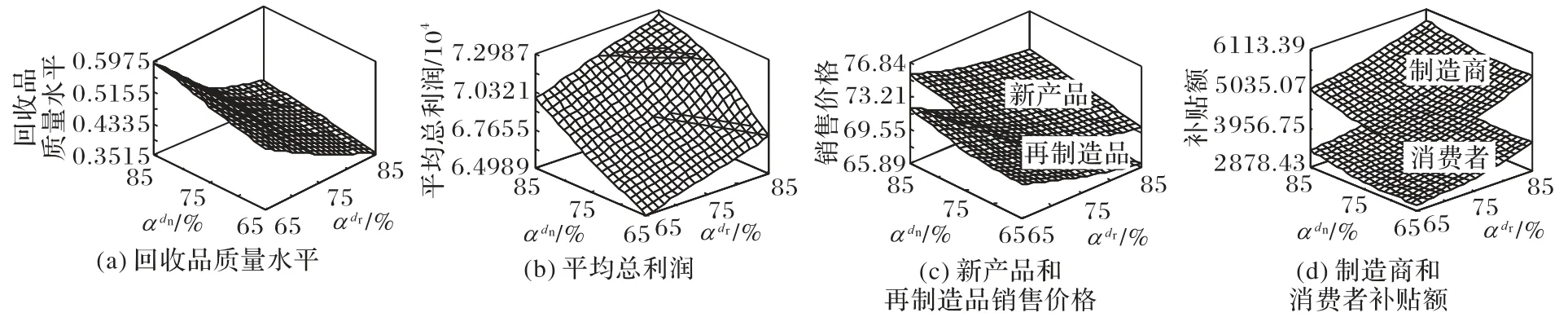
图4 不同潜在需求置信水平对最优决策的影响Fig.4 Influence of different confidence levels of potential demands on optimal decision

图5 不同潜在需求置信水平下的最优销售渠道和渠道结构Fig.5 Optimal sales channels and channel structures under different confidence levels of potential demands

4 结语

基于不确定市场需求和回收品质量水平，综合考虑政府差别权重补贴和直销平台费用，构建了四种销售渠道结构下的闭环供应链系统总利润模型，研究了闭环供应链系统的最优决策问题。采用PSO算法和GA对比求解模型算例，验证了算法的效度和模型的信度。

本研究可为企业在不确定环境下制定回收、生产和销售策略提供参考，同时为企业选择最优销售渠道结构提供借鉴。本文采用PSO 算法和GA 求解模型，进一步研究可以考虑ACO算法、ABC算法等其他元启发算法。