基于脉冲位置幅度调制的距离速度同时测量
黄少伟,黄婉琳,雷闰龙,毛雪松*
(1.肇庆学院计算机科学与软件学院/大数据学院,广东肇庆 526061;2.武汉科技大学信息科学与工程学院/人工智能学院,武汉 430081)
0 引言
车辆行驶的智能化是汽车工业发展的重要方向,实现方式上包括自主式和网联式两个大类[1-2],其中自主式智能驾驶要求通过测量装置获取道路中障碍物的位置和速度,用于计算出一条安全的行驶路径[3]。测量包括主动和被动两种方式[4],主动测量方式由测量装置发射电磁波,并通过接收反射电磁波来获取障碍物的特征参数;被动测量方式由测量装置的接收器感知障碍物的自然特性,如反射自然光、辐射热等来获取障碍物的特征参数。被动测量方式通常能获得很高的解像度,但受环境因素干扰较大;主动测量方式虽然不能获得被动测量方式的解像度,但受外部因素干扰小,测量的准确度更高。主动测量的典型装置有毫米波雷达和激光雷达,毫米波雷达采用发射频率调制连续波的方式实现障碍物距离和速度的同时测量[5-6]。由于毫米波雷达的空间解像度较差,单位时间内的测量次数不必很多,因此完成一次测量的发射信号长度可以较长[7-8]。与毫米波雷达相比,激光雷达的空间解像度可提高近两个数量级,因而要求在更短的时间内能够完成一次测量[9]。市场上大多数激光雷达采用发射短脉冲的方式完成目标距离的测量,但因脉冲长度过短,不能覆盖移动目标产生的多普勒信号一个周期,无法直接测量目标的速度。增大脉冲长度可以实现激光雷达的速度测量,但这样做一方面使距离分辨率劣化[10],另一方面向空间辐射大量无助于目标检测的电磁能量,因此需要研制一种在光电器件上可以实现的、长度介于频率调制连续波和短脉冲之间的测量信号波形,使激光雷达能够保持较高的空间解像度,并完成对道路场景中障碍物距离和速度的测量。
测量信号波形分为连续波和脉冲序列两大类,文献[11-12]中研究了连续波方式实现激光雷达距离和速度同时测量;但这些研究没有考虑智能驾驶要求完成一次测量的信号波形非常短,通常只有几微秒,也没有考虑连续波方式在驾驶环境中存在的干扰问题。相对来说,脉冲方式的干扰概率远低于连续波方式,因此本课题组提出了几种基于脉冲序列调制的激光雷达距离和速度同时测量方法[13-15],并通过仿真实验验证了这些方法的正确性,从理论上讨论了这些方法用于道路环境中目标检测的可行性与可靠性;但这些方法存在一个共性的问题,即计算外差信号多普勒频率时,需要根据距离测量结果确定外差信号中目标回波的头位置。在实际应用中,距离测量虽然使用数据累加方法增强目标回波信号检测能力,但对接收机输出信号信噪比(Signal-to-Noise Ratio,SNR)的要求远远高于傅里叶解析。通常距离测量要求信噪比约为0 dB,而傅里叶解析在信噪比为-30 dB 的情况下仍能计算出淹没在噪声中信号的频率。因此,设计一种方法使速度测量独立于距离测量具有非常重要的现实意义,当某个方向检测到存在运动目标,但未能检测出距离时,可自动增加该方向测量信号的发射功率,提高激光雷达对环境的自适应能力。
针对上述问题和应用需求,本文在前期工作的基础上,提出了一种在发射端同时调制脉冲位置和幅度的方法,即根据伪随机码“1”码的位置确定发射脉冲的位置,根据相邻“1”码的间隔确定发射脉冲的幅度,实现对接收端输出外差信号做频率计算时,无须根据距离测量结果确定外差信号的头位置,也无须根据速度测量结果来修正目标的距离,从而使距离测量和速度测量相互独立。
1 系统框架与问题描述
激光雷达测量装置的系统框图如图1 所示,包括激光器、发射端、接收端、调制部分和信号处理部分等模块,图中的PD表示光电转换器。调制码发生器产生发射波形所需的位置幅度调制码型,并作用于光外部调制器上,使发射端发射位置幅度调制的光信号。通常光调制器输出光信号幅度只有几毫瓦,为提高激光雷达对环境的测量能力,需要在调制器后增加光放大器提高发射信号的峰值功率。接收端使用光分离器将接收到的光回波信号分为两路:一路用于距离测量,另一路用于速度测量。选择使用双检测器结构是因为光信号的频率很高,1 550 nm 波长激光的频率高达1.9×1014Hz,因此必须使用相干检测的方式输出包含于回波信号中的多普勒频率。另一方面,相干检测输出的多普勒频率对回波的脉冲序列产生幅度调制效应,脉冲序列中靠近多普勒正弦信号零点的脉冲受调制影响幅度明显降低,对距离测量性能产生影响。
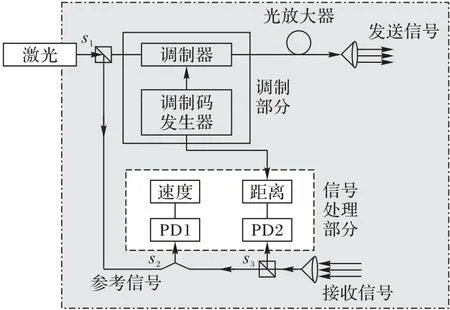
图1 激光雷达原理框图Fig.1 Laser radar priciple block diagram
对于采用伪随机码调制的激光雷达,文献[13]提出了非等间隔采样信号频谱分析方法:

可以计算出PD1 输出外差信号的多普勒频率,测量出目标的速度,其中f(ti)表示伪随机码“1”码位置对应的信号幅值,ΔTi表示相邻“1”码之间的时间间隔。与傅里叶变换的计算公式对比,可以看出为了计算多普勒信号的频率,需要将PD1 输出外差信号“1”码对应幅度倍乘相邻“1”码的时间间隔。如果PD1 输出的外差信号淹没在接收器的噪声中,则无法确定“1”码的位置,故不能用式(1)计算外差信号的频率。为确定外差信号头位置(头位置确定,则所有“1”码位置就可以确定),要利用PD2输出信号并结合PD2和PD1之间固定的时延等信息计算出目标距离。如果目标距离不能正确测量,则目标速度就不能正确测量。
2 距离速度测量方法
2.1 速度测量
PD1输出回波信号与本地信号的混频信号可表示为:
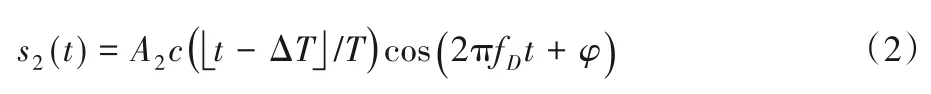
其中:φ包含因时延引起的相位变化;c(·)表示调制码;T表示码元宽度;ΔT表示从发射到接收之间的时延;表示向下取整。在调制码为“1”的码元区间内,s2(t)的采样值与多普勒余弦信号A2cos(2πfDt+φ)一致;但在“0”码元区间内,s2(t)的采样值为0,偏离多普勒余弦信号值。为了能够在接收端利用快速傅里叶变换(Fast Fourier Transform,FFT)方法计算出多普勒频率,需根据式(1)对“1”码元区间内采样信号幅值做修正。文献[14]即为利用该方法,根据距离计算结果确定回波信号的头,从而确定每个“1”码所在的位置。为了使速度测量不依赖于距离测量的结果,可以将幅值修正过程调整到发射端,构成新的调制码,如图2 所示。发射脉冲的位置由伪随机码“1”码的位置决定,脉冲的幅度由相邻码符号之间的关系决定:如果“1”码的后续码元为“1”码,则保持原码幅度不变;如果“1”码的后续码元为“0”码,则统计“0”码的个数;如果“1”码的后续码元“0”码个数为Ni,则将该“1”码的幅度乘以Ni+1。如果连“0”码的个数过大,则前面的“1”码幅值会过大,导致光器件无法实现过大功率光信号,因此需要在连“0”码过大的位置插入“1”码,本文选择最大连“0”码个数为3。
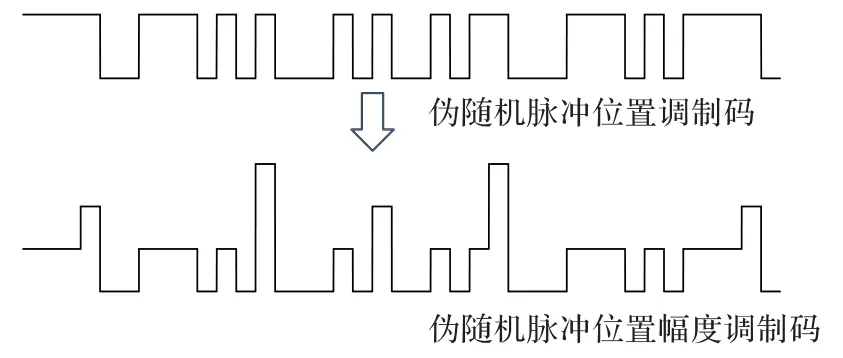
图2 调制码的格式Fig.2 Format of modulation codes
电光调制器输出光强度与调制电压之间的关系[16]为:

式中:a为插入损耗;Iq为输入光强度;I(t)为输出光强度;V(t)为射频端口的调制电压;Vπ为直流驱动电压。电光调制器后的光纤放大器在输入光功率变化较小的范围内可视为增益不变,因此放大后的光信号码元之间的幅度倍数关系可以与放大前码元之间倍数关系保持不变。为使调制器输出光信号幅度按照图2 的位置幅度关系变化,可以根据式(4)设置电光调制器的射频端口调制电压。

2.2 距离测量
激光雷达的发射端输出信号为:
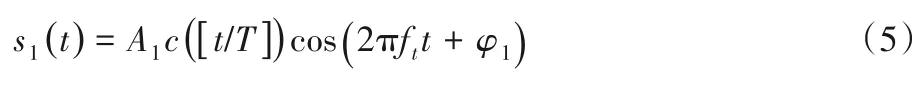
其中:A1表示发射信号的幅度,ft表示发射光信号的频率,φ1为初始相位。
由于光频率太高,接收端光电转换器PD2 只对光强度敏感,因此输出信号为:

其中:A2为PD2 输出电信号的幅度,n(t)表示接收电路的噪声。接收端距离测量部分信号处理器的任务是从光电转换器输出信号中测量出时延,并根据时延计算出目标的距离。由于信号s3淹没在噪声中,不能通过仪器直接给出时延的值。可以利用文献[14]计算相关函数确定峰值位置的方法,但是相关函数法需要按码元个数移位相乘再相加,运算量大。本文采用类似文献[15]处理Golomb 序列调制的数据累加方法来确定伪随机码调制的回波信号时延,可以降低运算量。
如图3 所示,第一行为PD2 输出信号,作为原理演示,忽略了噪声。信号处理部分检测调制码所有“0”码到“1”码的跳变时间点,记录相邻跳变点之间的时间间隔。然后,根据这些时间间隔,将PD2输出信号向左分别移位相应的时间,构成第二行、第三行……直到最后一个跳变点对应的行。最后将所有行相加,得到和信号,和信号中出现由最小值到最大值的跳变,该峰值跳变位置对应于回波信号相对于发射信号的时延。相比相关函数的方法,这种数据累加的方法需要移位的次数与从“0”码到“1”码的跳变次数相等,移位次数大幅下降,而且对信号运算使用加法,而不是乘法,运算量也大幅下降。统计表明,伪随机码的“0”码到“1”码的跳变次数约为码长的1/4。

图3 脉冲位置幅度调制的数据累加方法Fig.3 Data accumulation method for pulse position and amplitude modulation
3 仿真结果与分析
3.1 测量原理的仿真验证
假设激光雷达1 s 内完成测量20 万次,最大测量范围为150 m,则可取测量信号序列时长为4 μs,等待时长为1 μs。取调制码的码元宽度为2 ns,则完成单次测量的调制码序列包含2 000 个码元。另一方面,假设激光雷达的发射波长为1 550 nm,运动目标的相对速度在0~360 km/h 范围内,则相对运动产生的多普勒频率在0~129 MHz范围内。对每个码元采样一次,则129 MHz 信号一个周期内可采样点数大于3,测量信号长度可覆盖多普勒信号500 多个周期,因此可以完成高频信号频率的计算。多普勒频率低于一定值的情况下,可以认为被测对象相对静止,这类目标只需测出相对距离即可。智能驾驶中期望测量的最低速度为人的步行速度,取1 m/s,仿真中取测量信号长度为5 μs,因此可以测量出的最低速度为0.2 m/s,可以满足智能驾驶对速度参数的要求。
图4 给出PD2 输出信噪比为0 dB 情况下,利用图3 所给的数据累加算法获得的结果。在信噪比为0 dB 的情况下,信号淹没在噪声中。经过数据累加后,则出现一个明显的最小值跃迁到最大值,利用此特征来判断测量信号的飞行时间对应的信号延迟。由于激光光束很窄,非球面透镜的发散角可以做到0.1 mrad 左右,这样即使在100 m 远处,光束的宽度只有1 cm,因此在一个光束内出现两个目标的概率可认为是零。在不考虑回波信号二次反射的情况下,PD2 的输出信号中不会出现两个目标反射信号的叠加。即使考虑二次反射,通常二次反射信号非常弱,其影响可忽略不计,因此在一次测量中只需找出一个目标即可。通过寻找数据累加得到的信号中最大值和最小值,并检验最大值和最小值时间间隔的方式即可判断出信号幅值最大值位置是否对应目标距离。
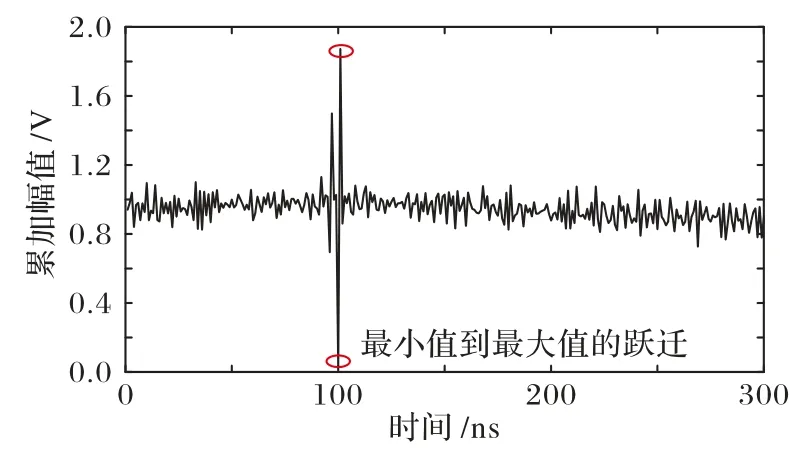
图4 信噪比为0 dB的情况下数据累加后的信号Fig.4 Signal obtained by data accumulation when SNR equals to 0 dB
为完成速度测量,可分析PD1输出信号的多普勒频率,在无噪声的情况下,PD1 输出的信号为幅度被调制的余弦波。图5 的下图给出幅度被调制的、频率为1.29 MHz 的多普勒信号样本,上图给出一个周期的余弦信号细节表示。对这种形式的信号采样,虽然得到的不是余弦信号的等间隔采样信号,但由于信号幅值被预调制,因此可以直接使用快速傅里叶变换算法计算出余弦信号的频率。
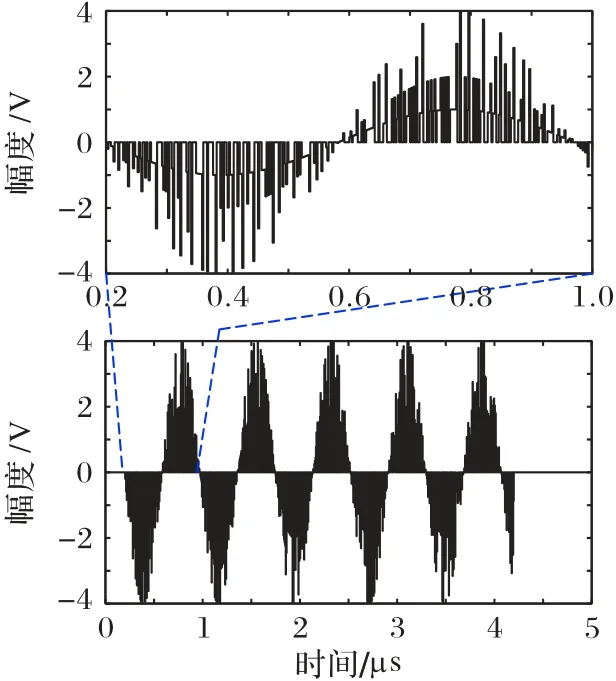
图5 PD1输出的外差信号Fig.5 PD1 output heterodyne signal
从每个脉冲序列的发射时刻开始计时,对PD1 输出信号采样长度为5 μs 的数据样本,采样频率为500 MHz。当信号淹没于噪声中时,不同于文献[14]利用距离信息定位PD1 输出信号中回波的方式,本文方法对5 μs 信号直接做快速傅里叶变换求出多普勒频率。类似于文献[14-15],取多普勒频率分别为1.29 MHz、5 MHz、10 MHz、20 MHz、50 MHz、129 MHz这6 个频率做快速傅里叶变换,在信噪比为-13 dB 的情况下得到如图6所示的频率谱。

图6 多普勒信号频谱分析结果Fig.6 Spectrum analysis results of Doppler signal
3.2 可靠性分析
运用快速傅里叶变换和图3 所示的数据累加方法,对回波信号在信噪比为-40 dB 到0 dB 范围内各取样点处做10 万次速度测量和距离测量验证,统计给出发生速度测量和距离测量错误的概率。距离测量方面,将脉冲序列预先设定一个延时叠加到噪声中,然后通过改变脉冲序列的幅度改变信噪比,最后在不同信噪比下比较数据累加方法获得的峰值位置与预先设定的延时,如果二者不一致,则统计为测量错误。
速度测量方面,将傅里叶变换的正频率范围内频谱峰值对应的频率和负频率范围内频谱峰值对应的频率取绝对值并求平均,作为多普勒信号的频率。考虑到傅里叶变换本身存在频率计算误差,如果傅里叶变换计算得到的频率和实际多普勒频率相差0.2MHz,则统计为频率测量错误。对距离和速度的测量错误统计结果如图7 所示,当信噪比分别为0 dB和-13 dB 时,距离测量和速度测量的误检测概率降为0,表明速度测量所需的信号功率比距离测量所需的信号功率低一个数量级,图1中PD2下方的光分离器可选分光比为90∶10。

图7 距离测量和速度测量在不同信噪比下的误检测概率Fig.7 Error detection rates of range and speed measurement under different SNR
距离测量误差取决于脉冲的宽度和检测装置的硬件电路两个方面,硬件电路的讨论超出本文的范围。脉冲的宽度可以决定距离测量的分辨率,与前期工作[15]一致,本文选取的脉冲宽度为2 ns,因此在硬件电路相同的情况下,所得的距离分辨率相同。速度测量方面,本文仿真中选取的脉冲序列长度为4 μs,比文献[15]中的1 024 ns 时间窗口更长,因此测量精度更高。图8 给出利用FFT 分析余弦等间隔采样数据和PD1输出数据频率在1 MHz 到129 MHz 频率范围内的误差对比,仿真中选取的频率增量步长为0.1 MHz,因此即使进一步降低频率增量步长,PD1 输出数据利用FFT 获得的频率误差不会超过0.2 MHz,对应速度误差0.16 m/s,可以满足智能驾驶车辆环境感知的需求。

图8 FFT分析PD1输出数据与余弦等间隔采样数据的频率误差对比Fig.8 Comparison of frequency error between PD1 output data and cosine uniform sampling data by FFT
对PD1 输出信号做傅里叶变换,得到的峰值可能来自多普勒信号,也可能来自噪声。图7 给出当信噪比大于-13 dB时可以确保频谱的峰值均来自多普勒信号,因此对含噪信号在大于信噪比-13dB 的情况下计算频率误差,并与无噪声情况对比,结果表明噪声不构成频率计算误差的影响因素。
4 结语
激光雷达在道路环境信息感知的应用中,目前只能测量目标的距离,而不能测量目标的速度。前期工作提出的伪随机码调制方法从理论上可以实现激光雷达距离和速度同步测量,但是速度的测量必须建立在距离正确测量的基础上,如果距离测量出现较大随机误差或测量数据丢失,则不能完成速度的测量。本文提出了一种利用伪随机码调制激光雷达发射信号脉冲序列位置和幅度的方法,并针对PD2 输出波形特征设计数据累加,获得目标反射回波信号的飞行时间。对PD1输出采样获得的非等间隔多普勒信号直接使用快速傅里叶变换方法,可计算出多普勒频率。用计算机仿真的方法在多个信噪比下对距离和速度测量的稳定性进行分析,并与前期基于伪随机码调制的方法对比,验证了方法的可靠性。与前期工作对比,本文的主要工作在于使速度测量独立于距离测量,在距离测量失败的情况下,也可独立完成目标速度测量。由于速度测量对信噪比要求较低,通常速度测量会更稳定,当检测到某个方向存在运动目标,但无法测出目标距离时,可通过算法控制提高该方向发射信号功率,实现目标距离的测量,增强激光雷达的智能化。

