基于混沌麻雀搜索算法的无人机航迹规划方法
汤安迪,韩 统,徐登武,谢 磊
(1.空军工程大学研究生院,西安 710038;2.空军工程大学航空工程学院,西安 710038;3.94855部队,浙江衢州 324000)
0 引言
随着无人机(Unmanned Aerial Vehicle,UAV)技术的不断发展,国内外学者对于无人机作战应用的研究日益增多。无人机航迹规划是任务规划系统的关键部分,是一个典型的非确定性多项式(Nondeterministic Polynomial,NP)问题[1]。随着规划问题复杂度的不断增加,其难度和计算量迅速增长,很难找到一种有效应对所有复杂环境的航迹规划方法。为解决不同条件下的航迹规划问题,学者们不断对航迹规划算法进行研究和改进。文献[2-8]研究了快速扩展随机树(Rapidexploration Random Tree,RRT)算法、A star 算法、粒子群优化(Particle Swarm Optimization,PSO)算法、遗传算法(Genetic Algorithm,GA)在UAV 航迹规划中的运用。Yang 等[2]将环境势场引入RRT 算法,但得到的规划航迹与实际最短航迹有一定差距;刘华伟等[3]将人的智能决策引入RRT算法,但是该算法依赖人的主观判断,容易陷入局部最优;赵锋等[4]将启发式权重系数引入A star 算法,但权重系数的线性调整策略不能很好地适应复杂的优化问题;Zhang 等[5]在PSO 算法中设置异步变化学习因子,但搜索能力依赖于步长的分段设置;程泽新等[6]在GA 中引入差分进化策略,但改进后的算法计算量增大,航迹规划实时性较差。
自1975 年美国教授Holland 根据达尔文进化论以及自然界优胜劣汰机制提出了GA 以后,越来越多的学者通过对不同生物种群和物理现象进行分析,从中获取灵感,提出了多种群智能优化算法,包括:灰狼优化算法(Grey Wolf Optimizier,GWO)[7]、萤火虫算法(Firefly Algorithm,FA)[8-9]、天牛须搜索(Beetle Antennae Search,BAS)算法[10]、鲸鱼优化算法(Whale Optimization Algorithm,WOA)[11]、天牛群优化算法(Beetle Swarm Optimization,BSO)[12]。
麻雀搜索算法(Sparrow Search Algorithm,SSA)[13]通过麻雀个体搜寻食物和反捕食进行迭代寻优,具有调整参数少、收敛速度快、计算简单等优点;但和其他群智能算法一样,在求解复杂工程优化问题时,容易“早熟”,导致收敛精度不高,且易于陷入局部最优解。SSA 的更新方式可大致分为两种:1)向当前最优位置靠近;2)向原点靠近。通过仿真实验可知,在进行航迹模型最优航迹求解时,每次收敛是直接跳跃到当前最优解附近,容易丢失全局最优航迹解,仅可能得到满足约束的可行解,并且有概率得不到可行解。为了改善全局搜索能力,防止陷入局部最优解,借鉴Xu 等[14]引入混沌算子的思路,本文将立方映射混沌算子[15]引入SSA算法,提出了一种混沌麻雀搜索算法(Chaos Sparrow Search Algorithm,CSSA)。CSSA 在对麻雀位置初始化过程中使用混沌序列,同时使用反向学习策略(Opposition-Based Learning,OBL)[16],有效保证了初始种群的均匀性;使用精英反向学习策略扩大在精英反向解所在区域内的搜索,增强全局搜索能力,并引入正弦余弦算法(Sine Cosine Algorithm,SCA)[17],对追随者位置更新进行优化,增强种群多样性,有利于算法跳出局部最优和快速收敛;对警戒者数量进行线性递减,平衡算法全局和局部搜索能力;当算法陷入停滞时,采用高斯游走策略帮助算法跳出局部最优。最后通过15 个基准测试函数验证了CSSA 的优越性。同时在威胁环境下进行航迹规划仿真,并与PSO、SSA、WOA、BSO、GWO等对比,仿真结果验证了所改进算法的有效性。
1 麻雀搜索算法
SSA 主要模拟了麻雀觅食的过程。麻雀觅食过程是发现者-跟随者模型的一种,同时还叠加了侦查预警机制。麻雀中容易找到食物的个体作为发现者,其他个体作为跟随者,同时种群中选取一定比例的个体进行侦查预警,如果发现危险则放弃食物,安全第一。由文献[13]可知,SSA 是一种优于GWO、PSO、引力搜索算法(Gravity Search Algorithm,GSA)等算法的一种新的群智能优化算法。
SSA 算法中有发现者、追随者以及警戒者,分别按照各自规则进行位置更新,更新规则如下:
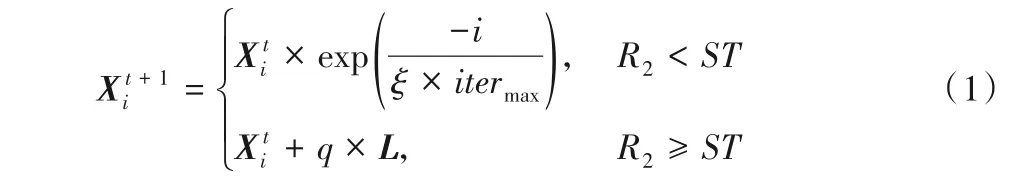
其中:t为当前代数表示在t+1 代第i只麻雀的适应值;itermax是最大迭代数;ξ∈(0,1)是一个随机数;R2表示警戒值;ST表示安全阈值;q是一个服从正态分布的随机数;L是一个一行多维的全一矩阵。
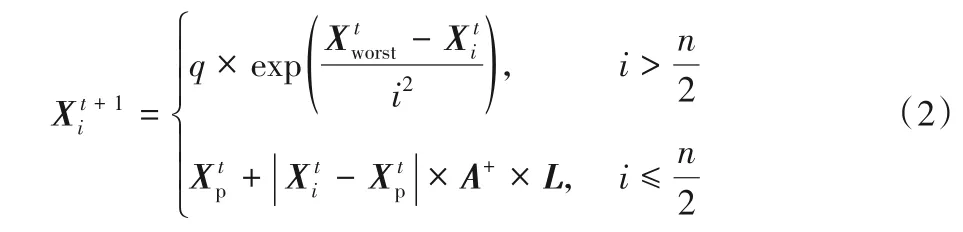
其中:Xp表示被发现者占据的最佳位置;Xworst表示当前最差位置;A是一个各元素为1或-1的一行多维矩阵。

算法实现具体如下:

2 改进的麻雀搜索算法
2.1 立方混沌映射
SSA 和其他智能算法一样,在求解复杂优化问题时,在迭代后期种群多样性降低,易于陷入局部最优,导致收敛精度不高。为了提高算法全局搜索能力,避免迭代后期种群多样性降低,考虑到混沌算子具有随机性与规律性的特点,且能在一定范围内不重复遍历所有状态,采用混沌算子初始化种群,从图1 可以得知立方映射比Logistic 映射的均匀性要好,因此采用立方映射混沌算子。立方映射公式如下所示:
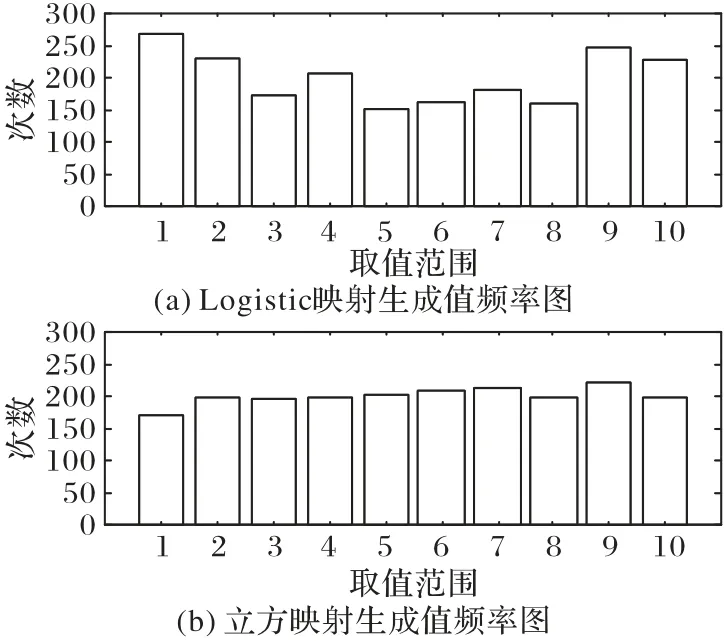
图1 映射对比图Fig.1 Mapping comparison diagram
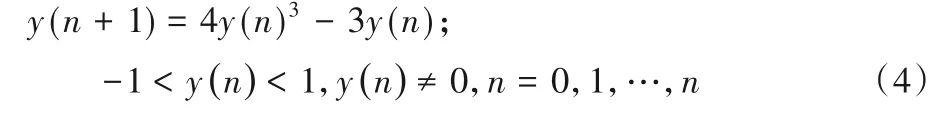
初始化麻雀种群由M个d维个体组成,采用立方映射初始化麻雀种群的具体方法为:随机产生一个每维均为-1 到1的d维向量y1作为第一个个体,之后用式(4)对第一个个体的每一维进行迭代得到剩余(M-1)个个体,最后使用式(5)将立方映射产生的变量值映射到麻雀个体上。

其中:Xlb、Xub为每个个体在各个维度上的上下边界;Xi为实际个体变量值。
2.2 精英反向学习策略
OBL 是近年来计算智能领域出现的一种新策略,研究表明反向解更接近全局最优解的概率比当前解高出50%,使用该策略能够有效增强种群多样性,防止算法陷入局部最优。
精英反向学习策略(Elite Opposition-Based Learning,EOBL)则是针对OBL不一定比当前搜索空间更易搜索到全局最优解这一问题提出的,该策略利用优势个体来构造反向种群,以此增强种群多样性。

利用动态边界来代替搜索空间的固定边界,能够积累搜索经验,使生成的反向解位于逐步缩小的搜索空间,加速算法收敛。当生成的反向解位于边界之外时,使用随机生成的方法进行重置。如式(9)所示:

2.3 正弦余弦算法
正弦余弦算法(SCA)是利用正弦函数与余弦函数的震荡特性进行寻优,其优点是收敛性好,易于实现。
SCA 首先随机生成N个搜索个体,依据适应度函数计算每个个体的适应度,将适应度最好的个体记为最优个体X*,寻优过程中个体位置更新公式为:
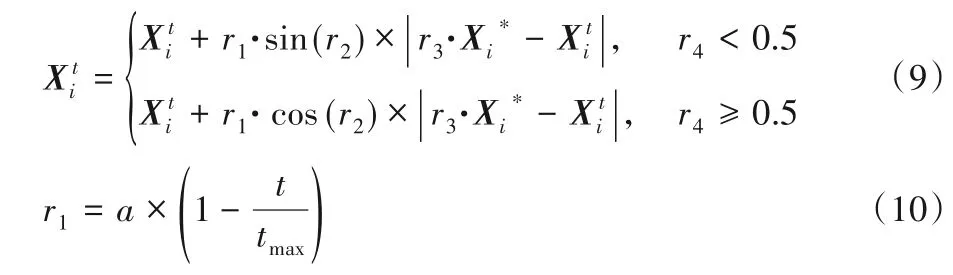
2.4 改进的麻雀搜索算法
针对SSA 存在的不足,首先使用立方映射混沌算子进行种群初始化,并利用反向选择策略生成初始反向解加入初始种群,从其中选择最优的N个个体作为最终的初始种群。利用精英反向学习策略对麻雀种群中的发现者进行选择,以此提高发现者种群的质量,发现者作为种群中的优势群体,利用精英反向学习策略,能够增强其多样性,为较好的全局搜索奠定基础,同时可以利用反向解引导算法跳出局部最优,并且通过动态边界不断缩小搜索空间,有利于提高算法收敛速度。
另外,在保留SSA追随者觅食和争夺机制的基础上,利用SCA 对其进行改进。在觅食和争夺机制中,追随者向最优位置的移动是跳跃式的,这种方式虽然有助于算法后期收敛速度的提升,但是也容易导致种群在短时间内迅速聚集,降低了种群多样性,易于陷入局部最优。利用SCA 进行追随者位置更迭,可以减少搜索盲点。
警戒者的存在能够增强算法的全局搜索能力,但是其数量在迭代过程中保持不变,会导致算法后期收敛速度减慢,因此采用线性递减的方式对警戒者数量进行控制:在算法初期,数量多,有利于全局搜索;在算法后期,减少警戒者数量,有利于算法的收敛。警戒者数量线性递减公式如下:

其中:Num为当前警戒者数量,Numini为初始警戒者数量;t为当前迭代次数,tmax为最大迭代次数。
当算法陷入停滞时,采用高斯随机游走策略生成新个体,以此帮助算法跳出局部最优。位置生成公式如下:
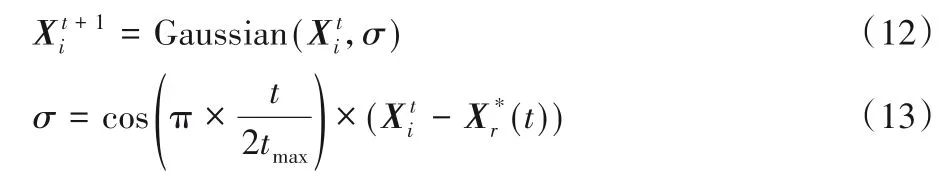
CSSA流程如图2所示。

图2 CSSA流程Fig.2 Flowchart of CSSA
3 航迹规划问题
3.1 航迹规划原理
航迹规划的最主要目的就是在已知飞行区域内产生一条能够在规定时间内从起飞点(U)到达目标点(T)、且有效避开敌方威胁区域的最优航迹。通过采用离散航迹点并将航迹点进行连线得到一条满足约束的最优航迹,如图3,由于是点与点之间的连线段,需要进行航迹平滑处理,后续仿真实验采用B样条曲线[18]进行处理。
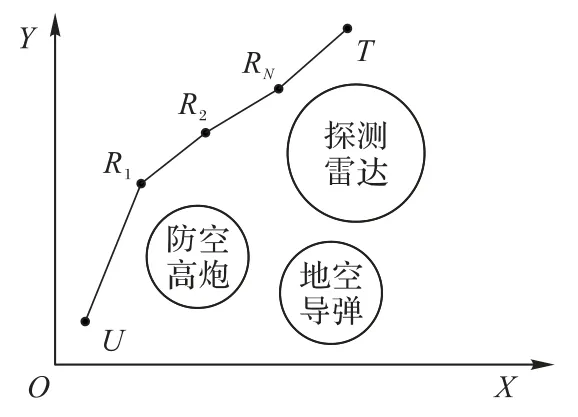
图3 航迹规划原理Fig.3 Principle of path planning
3.2 坐标系转换
传统二维航迹规划考虑两个方向上的变量,为简化研究问题维数,对二维航迹规划问题进行降维处理,以UAV起点U为坐标原点,将起点U和目标点T连线作为横轴,垂直于线段UT作纵轴,建立新的坐标系,如图4 所示。在图4 中,将线段UT等分为N+1份,则转换后的航迹点横坐标已知,只需求解出航迹点纵坐标,将得到的横纵坐标转换到XOY坐标系中,即可得到所规划航迹点,最后通过平滑曲线处理即可得到可行航迹。
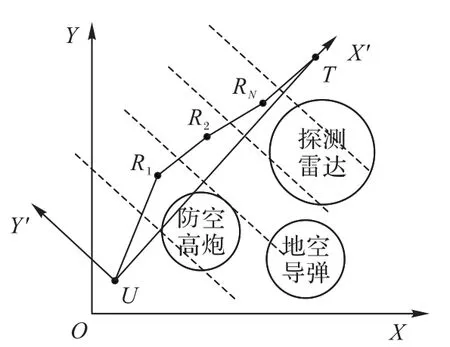
图4 坐标系转换Fig.4 Transformation of coordinate system
3.3 B样条曲线
B样条曲线是贝塞尔曲线的一般化形式,公式如下:

其中:m是节点zi的个数,zi的取值范围是{z0,z1,…,zm-1} 并且x0≤x1≤…≤xm-1;Pi是控制节点,共有m-n-1 个控制节点;Li,n表示n阶的B样条基数,公式如式(15)、(16)。
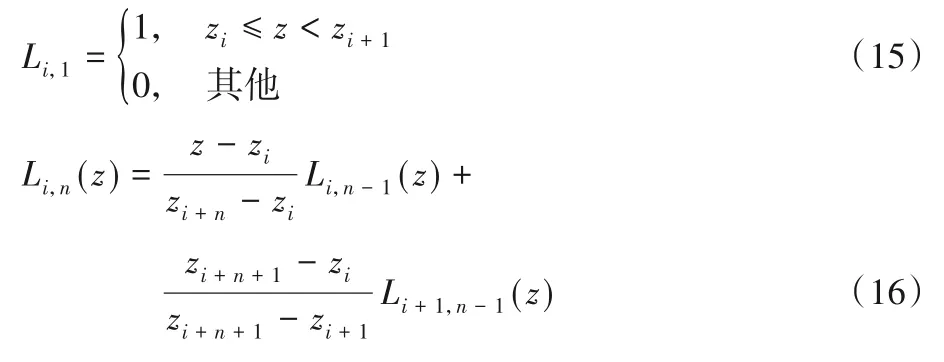
B 样条曲线的计算成本较低,能够控制样条形状,易于保证路径连续性。而Dubins 曲线不具有曲率连续性,贝塞尔曲线稳定性不够,因此仿真实验选用B 样条曲线处理航迹平滑任务。航迹平滑效果如图5所示。

图5 B样条曲线航迹平滑效果Fig.5 Effect of B spline curve path smoothing
3.4 约束函数和适应度函数
基于智能优化算法随机生成的种群个体不一定符合搜索空间的要求,需要建立合适的适应度函数并考虑各种约束,用来淘汰种群中不符合约束的个体,从而获得较优个体。静态全局航迹规划主要考虑UAV 的油量代价、飞行高度代价以及威胁代价;同时需要考虑到UAV 自身性能,如最大转弯角、最大俯仰角。本文建立二维航迹规划的目标函数,故不用考虑最大俯仰角约束。
3.4.1 油量代价
UAV 在执行任务过程中考虑油量代价,是为了避免UAV在完成任务后没有足够燃油返航的问题。假定UAV 在任务中执行恒定速率,则油量与航迹长度成正比,表示为如下代价函数:
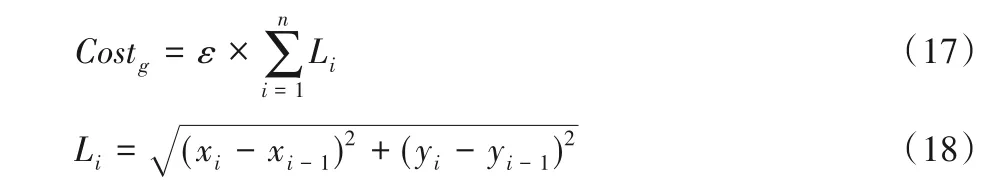
其中:ε为油量约束和航迹长度的比值为相邻航迹点连线段之和,航迹长度采用欧几里得距离,Li为第i段二维航迹距离;(xi,yi)为第i个航迹点的坐标。
3.4.2 威胁代价和禁飞区约束
UAV 在执行任务时会遇到敌方的防空系统,其中包括探测雷达、防空高炮、地空导弹等威胁,将上述威胁在二维平面上近似看作一个个圆形区域,探测范围或打击范围作为其半径,规定UAV不能通过圆形区域。
采用如下方法判断是否穿过威胁区:
1)分别计算两相邻航迹点与威胁源圆心距离D1和D2。
2)情况一:D1、D2有一个或两者都小于威胁源半径r,则穿过该威胁区,如图6(a)。
3)D1、D2均大于威胁源半径r,则计算威胁源心和两航迹点连线距离D3。
4)情况二:若D3≥r,则不穿过该威胁区,如图6(b);若D3<r,则计算威胁源圆心到相邻航迹点连线段中点距离D4。
5)情况三:D4≥r,则穿过威胁区,如图6(c)。
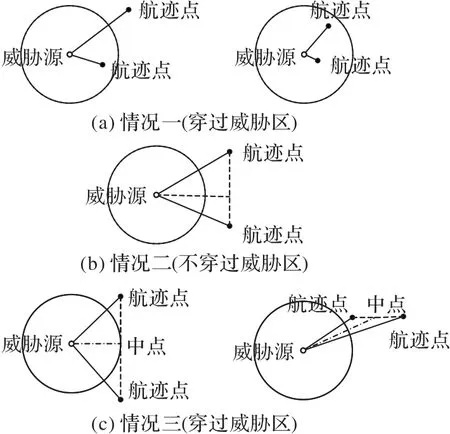
图6 威胁区穿越判断Fig.6 Judgment of crossing threatened zone
3.4.3 最大转弯角约束
由于UAV 性能限制,实际飞行的最大转弯角不能无限制[19],同时在转弯过程中,无人机会稍微偏离规划的航迹,此时航迹曲率就要被考虑,所以要求生成的相邻航迹段间的夹角不能超过最大转弯角,在仿真实验中规定最大转弯角为60°。
3.4.4 最大航程约束
假设UAV 执行任务后需要原路安全返回基地,那么UAV携带燃油要能够进行往返飞行,设定最大航程为550 km。
综上,航迹规划目标函数模型如下:

其中:σ为威胁惩罚系数,即生成航迹不满足约束时,代价会剧增,在仿真实验中设σ为10E+5。
4 仿真与验证
4.1 算法测试
为了验证改进算法的先进性,分别采用PSO、BSO、WOA、GWO、SSA 和CSSA 对测试函数进行求解,测试函数如表1 所示。上述实验均在Intel Core i5 CPU,2.50 GHz,16 GB 内存,Windows 10(64 位)的测试环境中进行,并采用Matlab R2016a软件编写。在测试中,将各算法的种群规模设为100,迭代总数设为500,各个测试函数的维度如表1所示。

表1 测试函数Tab.1 Test functions
分别对各个测试函数进行30次仿真实验,统计30次实.得到的平均值、标准差,如表2所示。

表2 算法测试结果比较Tab.2 Comparison of algorithm test results
其中F1~F7为单峰测试函数,主要用于测试算法的开发能力,分析这七个单峰函数求解情况可知,对于F1、F3、F4、F6四个测试函数,CSSA 寻优效果最佳,均能稳定得到全局最优解;对于F2、F5两个测试函数,CSSA 虽不能稳定收敛到最优解,但收敛效果和收敛精度优于对比算法,且F5作为一种极其复杂的病态测试函数,其全局最优解在一条香蕉型的峡谷上,谷中曲面上的最速下降方向与到达全局最优值的方向近似垂直,且山谷内的值变化不大,大部分优化算法很难找到全局最优解,而CSSA 在求解F5时明显优于其他算法;对于F7测试函数,CSSA 与其他对比算法差别不大。从整体上看,对于单峰测试函数,CSSA寻优效果优于其他算法,且稳定性较好。
F8~F15为多峰测试函数,其中F12~F15是固定维度函数。该类测试函数有多个局部最优解,智能优化算法在求解时易于陷入局部最优,因此多峰测试函数主要用于测试算法的探索能力。在求解F8时,六种算法对于该函数寻优效果均不理想,GWO 最优;在求解F9时,CSSA 优于三种算法;在求解F10、F11时,优于其他对比算法;在求解F12时,六种算法收敛效果相近,但CSSA 稳定性更好;在求解F13时,CSSA 和PSO 效果最佳,优于其余四种算法;在求解F14时,CSSA 效果仅次于PSO,优于其余四种算法;在求解F15时,CSSA、SSA、WOA 和GWO均能收敛到全局最优解,但CSSA稳定性更好。以上统计数据表明,CSSA整体寻优能力优于PSO、WOA、BSO、GWO和SSA。
为进一步分析六种算法的寻优能力,根据表2 的均值对算法在各个测试函数中的结果进行比较排序,若相等则比较标准差,结果如表3 所示,表最后一行为各算法的平均排序结果。CSSA 排序第一,六个算法中的寻优性能最强,且明显优于SSA。其余算法排序为:SSA、PSO、WOA、GWO和BSO。

表3 算法结果排序Tab.3 Sorting of algorithm results
为验证CSSA 的稳定性与收敛性,列出了F1、F3、F5、F9、F11和F14六个测试函数的箱式图和迭代收敛曲线图。
图7 为6 种算法独立运行30 次求解6 个测试函数得到的箱式图,由图知CSSA在求解时,均未出现异常点,并且收敛值的分布相对其余四种算法更加集中,明显优于对比算法,说明CSSA在求解问题时鲁棒性更强。

图7 不同算法在6个基准测试函数上的收敛箱式图Fig.7 Convergence box plots of different algorithms for six benchmark test functions
图8 为各算法收敛曲线图,实线为CSSA。在求解F1、F3、F5、F13时,CSSA 收敛速度优于对比算法;对于F9、F11,CSSA 收敛速度优于PSO、WOA、BSO、GWO 四种算法。由于F5的全局最优解较难求得,因此迭代后期收敛速度较慢。整体上CSSA收敛速度优于其他五种算法,且具有较好的收敛速度与收敛精度。
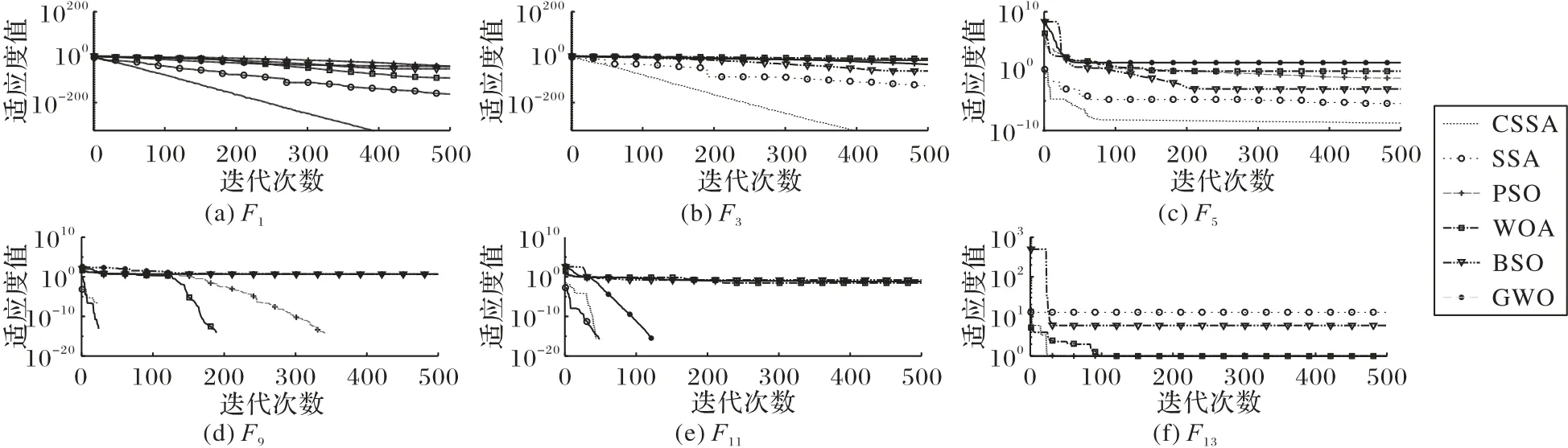
图8 各算法收敛曲线Fig.8 Convergence curves of different algorithms
4.2 仿真计算与验证
航迹规划问题实质上是一个非确定性多项式求解问题,运用CSSA求解航迹规划问题即用CSSA对目标函数进行求解寻优。麻雀种群代表航迹,每一只麻雀代表一条可能航迹,每只麻雀的维数代表航迹点的个数,每只麻雀的各维数值即为航迹点坐标值,麻雀个体适应度即为目标函数值,目标函数由代价函数和约束函数构成,麻雀种群中发现者是当前目标函数值较优个体,跟随者是当前目标函数值较差个体,通过对发现者和跟随者位置的更新,来得到麻雀种群的最优位置,进行若干次迭代寻优后,返回最优解即为所求最优航迹。
仿真实验环境为:Intel Core i5 CPU,2.50 GHz,16 GB 内存,Windows 10(64位)。
航迹规划模型参数设置如下:战场空间为xmax=100 km,ymax=100 km,航迹节点数Num=20,最大转弯角为60°,最大航程550 km,UAV 起点为(1 km,1 km),目标点为(95 km,90 km),威胁源参数如表4所示。
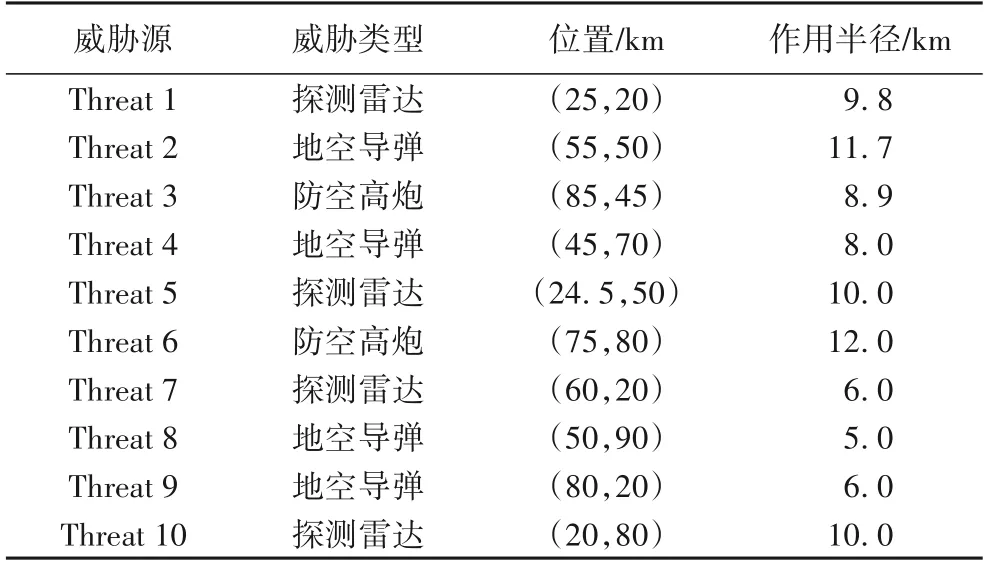
表4 威胁源参数Tab.4 Threat parameters
分别使用PSO、SSA、以及CSSA 对静态航迹规划模型式(19)进行求解,进而得到所需航迹。算法种群规模设置为100,每一个种群即为一条航迹,最大迭代数量为100,进行50次仿真实验。图9(a)~(c)分别为CSSA 规划航迹、SSA 算法规划航迹以及PSO 算法规划航迹,图10 为三种算法航迹规划迭代收敛曲线。仿真实验数据如表5所示。

表5 威胁环境下算法效率对比Tab.5 Comparison of algorithm efficiency under threat environment
由图9(a)~(c)比较可知,CSSA规划的航迹优于PSO算法和SSA 算法所规划航迹,CSSA 规划的航迹能够贴近威胁飞行,减少航迹代价。
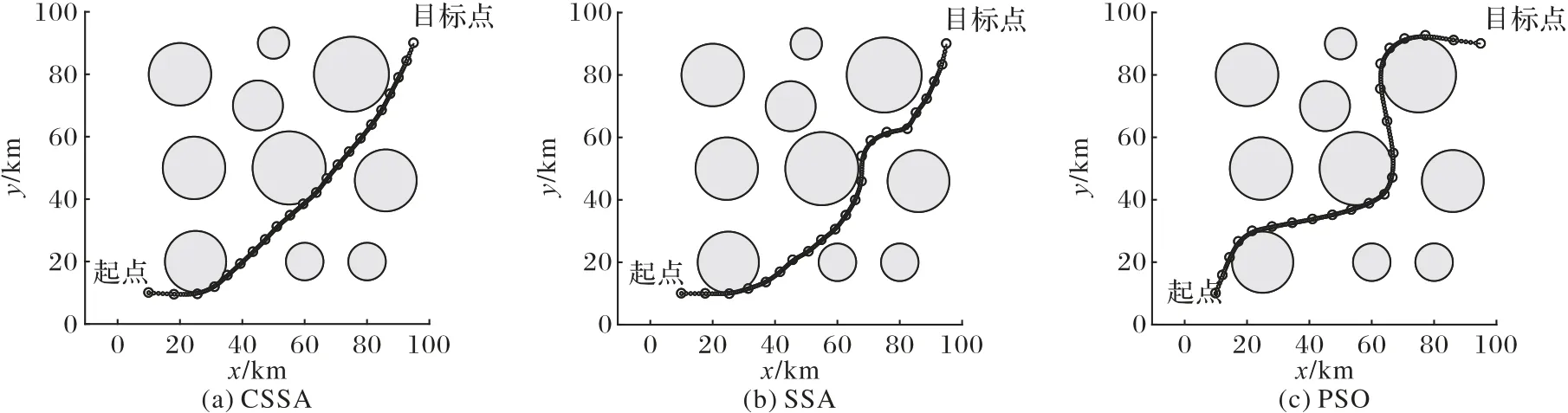
图9 三种算法航迹图Fig.9 Path charts of three algorithms
由图10 可知CSSA 在第50 代左右开始收敛,SSA 在第60代左右开始收敛,PSO在15代就开始收敛,说明PSO算法收敛较快,但CSSA 虽然收敛速度前期慢于PSO,但后期能够稳定收敛到最优值,且CSSA收敛速度快于SSA。

图10 三种算法迭代曲线对比Fig.10 Comparison of iterative curves of three algorithms
表5 表明CSSA 得到的平均适应值和最小适应值都低于PSO 算法和SSA 算法,并且能够稳定对航迹规划模型进行求解,从而得到一条代价最优、满足约束的安全可行航迹。
5 结语
本文提出利用改进麻雀搜索算法来解决UAV 航迹规划问题。麻雀搜索算法通过麻雀的搜寻食物与反捕食及位置更新来搜索最优解,将立方映射混沌算子、反向学习策略和正弦余弦算法引入到基本麻雀搜索算法中,采用多样改进策略,增加种群多样性,平衡算法的开发与探索能力,避免麻雀搜索算法陷入局部最优,从而找到全局最优解。函数测试表明,改进算法在求解质量上有明显提高,航迹规划仿真结果也表明,基于改进麻雀搜索算法的航迹规划能够有效跳出局部最优,并且提高计算速度,稳定地规划出一条可行高效的UAV 飞行航迹。

