基于机器学习的砂型铸造涂料悬浮率的预测

翟秀云，陈明通

（1.攀枝花学院智能制造学院，四川 攀枝花 617000；2.攀枝花学院公共实验中心，四川 攀枝花 617000）

在砂型（芯）工作表面上涂敷涂料是改善铸件质量的经济、实用且收效显著的方法[1-3]。随着机械制造、航空航天、石油化工、航海等行业的快速发展，对于高质量铸件的需求量越来越大，国内外砂型铸造涂料的研究也日益深入。传统的新涂料的研制方法为“炒菜”式方法，即凭经验决定涂料制备的配方和工艺，再通过反复的实验以获得所需性能的涂料，整个过程费时费力[4-6]。

上个世纪科学家们提出了“材料设计”的思想，即通过计算预报新材料的组分、结构与性能，或者说，通过理论设计来“定做”具有特定性能的新材料。运用基于机器学习的数据挖掘方法，对材料设计的相关数据加工处理，建立辅助新材料、新物质的预测模型，已经成为新材料设计的主流。在此基础上可以辅助新材料研制和新产品开发，达到“事半功倍”的效果[7-8]。近年来，机器学习在铸造涂料的设计研发、铸造工艺的优化中得到了成功应用[9-10]。

本工作中，收集了文献[9]中的铸造涂料悬浮率数据建立了数据集，利用多种机器学习方法构建悬浮率的预测模型：支持向量回归（Support Vector Regression，SVR）模型与反向传输神经网络（Back Propagation Neural Network，BPNN）模型。验证结果表明SVR 与BPNN 是实现铸造涂料悬浮率预测的非常有前途的建模工具。同时，本工作的方法可以为新的铸造涂料设计提供参考，并加快涂料开发的进度。

1 数据集与计算方法

1.1 数据集

铸造涂料悬浮率数据集来自于文献[9]，由12 个铸造涂料悬浮率（Y，93.0%～99.0%）样本组成。有14个涂料成分作为输入变量，分别为锆英粉、石英粉、铝矾土、镁橄榄、硅镁粉、石墨、棕刚玉、滑石粉、海泡石、97 悬浮剂、LA 悬浮剂、SN 悬浮剂、2123 树脂、铁红，用参数X1～X14 表示。数据样本详见参考文献[9]。将数据集分成两部分：用于建模的训练集和用于验证的测试集。在选择测试集数据时，有以下原则：

1）测试集样本的悬浮率即不是整个数据集中最大值也不是最小值，以避免超范围预测；

2）测试集样本数占样本总数的20%～30%.

为了遵循以上原则，把序号7 和12 的样本作为测试集样本，其余数据作为训练集样本。

1.2 支持向量回归

支持向量回归（SVR）[11，12]是解决非线性回归问题的有效方法，也是一种有监督的学习算法，已广泛应用于各个领域。其考虑了经验风险和预期风险之间的平衡，使计算模型具有良好的预测和泛化性能。在有限样本情况下，其目标是得到现在样本信息下的最优解，也是全局唯一的最优解。

回归模型中，目标是让训练集中的每个点（xi，yi）尽量拟合到一个线性模型yi=wφ（xi）+b.SVR 定义一个常量ε>0，SVR 的损失函数度量为：

SVR 目标函数的原始形式：

式中：C 是设定的惩罚因子值；ξi、ξi*为松弛变量的上限与下限。

接着求优化函数对于w，b，ξi、ξi*的极小值，再求拉格朗日乘子a，a*的极大值。求解后的目标函数如下：

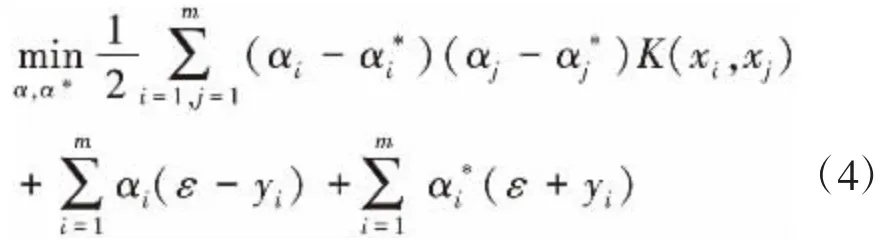
其约束条件为：

由此可得拉格朗日待定系数和，回归函数则为：

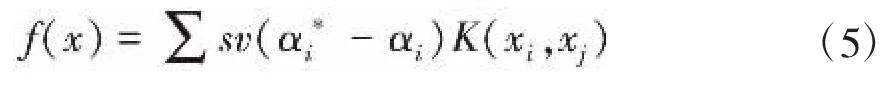
式中K 为核函数，本文中采用了径向基形式的核函数（Radial Basis Function，RBF），其表达式如下：

1.3 模型的评价

本文中所用的模型的评价指标有：均方根误差（Root Mean Square Error，RMSE）和平均相对误差（Mean Relative Error，MRE），计算表达式如下：

式中ei和pi分别为涂料的悬浮率的实验值与预测值；n 为样本的数量。

1.4 计算的实施

本次计算是在上海大学的材料数据挖掘在线计算平台（OCPMDM）上进行的[13]，可以免费使用，网址为：http：//matdata.shu.edu.cn/ocpmdm/，其前身为HyperMiner 软件包[14]，可从以下网址上免费下载：http：//chemdata.shu.edu.cn：8080/MyLab/Lab/download.jsp.

2 结果与讨论

2.1 变量筛选

变量筛选[11]是建立一个成功模型的关键因素，可以降低模型的特征空间维度，进一步降低过度拟合的风险，去除与目标值无关的特征和噪声干扰，还可以缩短训练时间，提高模型的预测能力和泛化性能。

本工作中，采用遗传算法（Genetic Algorithm，GA）[15，16]筛选自变量以形成最优特征集。GA 属于进化算法，是一种受自然选择过程启发的元启发式算法。与其他优化算法相比，遗传算法能够从响应面上的局部最优解出发，在不需要响应面上的知识或梯度的情况下，求解多种优化问题。

图1 说明了如何使用GA 搜索最优特征集。从图1 可以看出，SVR 算法经过8 次迭代后，最小的RMSE 出现，此时的最佳特征集包含了作为模型的输入的2 个参数（见表1），分别为X1（锆英粉）和X6（石墨）。

表1 用于建模的训练集与测试集

图1 GA 搜索最优特征集

2.2 模型的建立

2.2.1 RBF-SVR 模型

首先利用SVR 的留一法交叉验证（LOOCV）与网格搜索对RBF-SVR 的三个超参（C、ε 和γ）进行调优，他们的范围分别为1～100、0.01～0.1、0.5～1.5，步长值分别为2、0.02 和0.2，超参的网格搜索过程如图2 所示。当评价函数MRE=0.552 时为最小，此时，C=5、ε=0.01、γ=0.9.

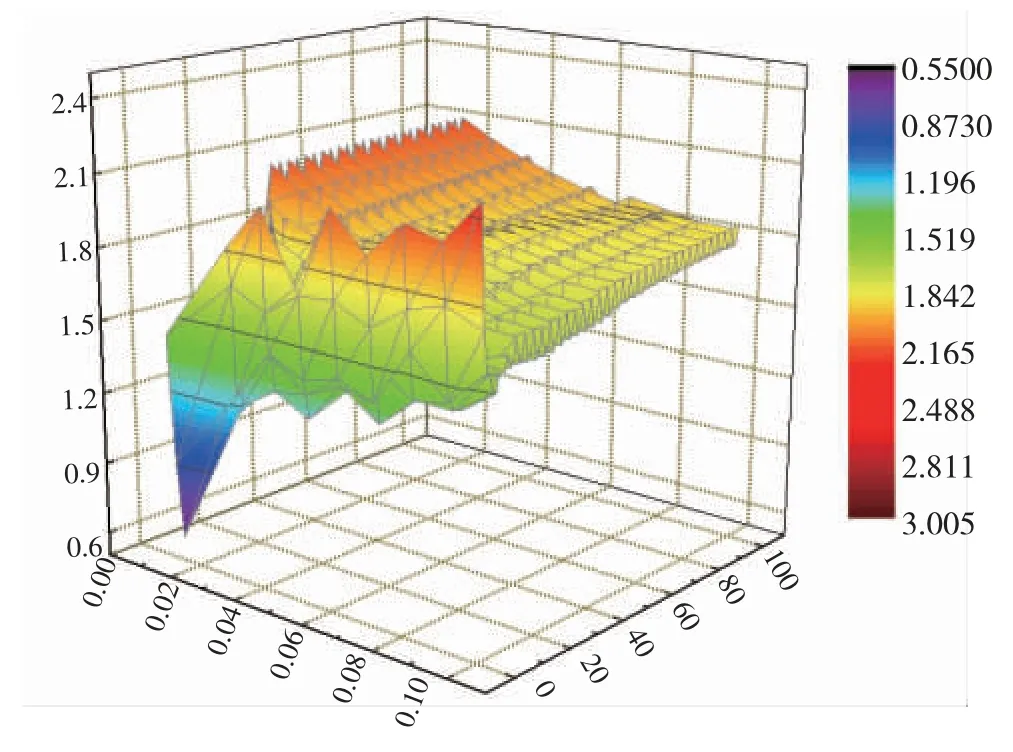
图2 RBF-SVR 模型的超参优化

利用最佳特征集和优化后的超参建立的RBF-SVR 模型如下：

式中：x 是未知向量，xi是模型的支持向量。n 和βi分别是支持向量的个数和拉格朗日乘子。

图3 对训练集与测试集样本的实验值和RBFSVR 模型的预测值进行了比较。从图中可以看出，模型的RMSE=0.892，相关系数R=0.959，决定系数Q2=0.889，训练集和测试集样本都非常靠近拟合线，说明模型具有极好的预测性能。此外，模型LOOCV的结果为：RMSE=1.009，R=0.931，Q2=0.858.以上数据说明所建的模型是预测铸造涂料悬浮率的一个非常有效的工具。

图3 悬浮率的实验值与RBF-SVR 模型的预测值

2.2.2 BPNN 模型

BPNN 模型的参数为：隐含层层数设为1，节点数2 个，输入、输出层节点数分别为2、1.模型的预测结果为：RMSE=0.177，R=0.998，Q2=0.995，LOOCV 的结果为：RMSE=1.634，R=0.836.图4 显示了训练集与测试集样本的实验值和BPNN 模型的预测值的接近情况，该图清晰地表明了BPNN 模型的预测性能和本文中的SVR 模型非常接近，都具很好的外推性。

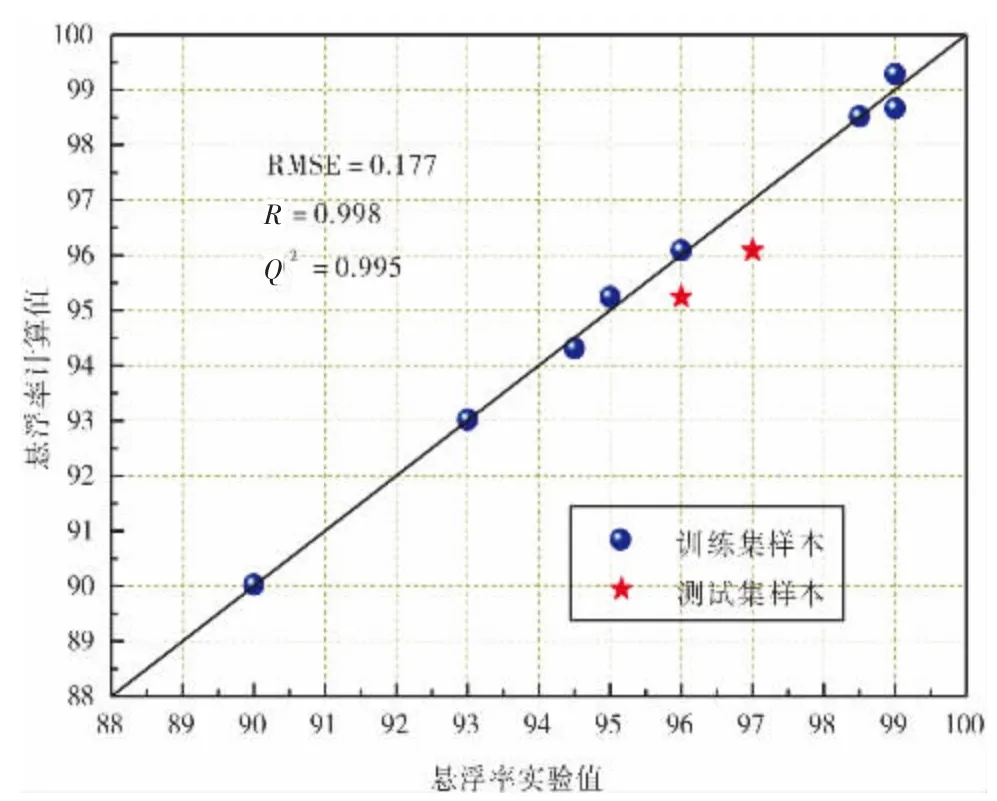
图4 悬浮率的实验值与BPNN 模型的预测值

BPNN 模型与RBF -SVR 模型对测试集的2组样本的预测值及对应的相对误差见表2 所示。从表2 中可以发现由于BPNN 模型对两个样本的预测值的相对误差的绝对值更小，所以其外部测试性能比RBF-SVR 模型更优。同时，由于两个模型的相对误差都比较小，说明他们的预测值都非常接近实验值，因此仅用两个自变量预测悬浮率是合适的。

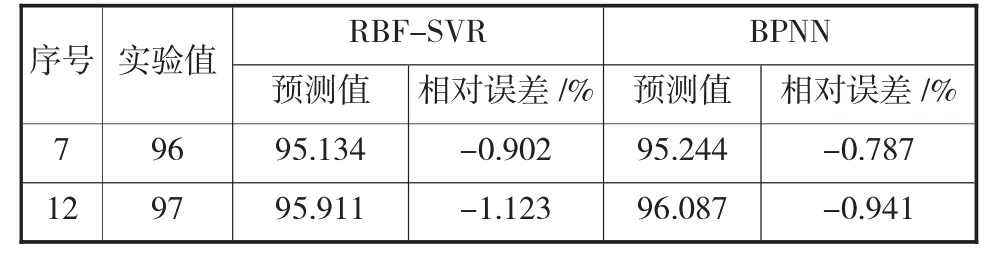
表2 两个模型对测试集预测的结果比较

3 结论

本工作中，利用收集的文献中的数据建立了用于预测铸造涂料悬浮率的样本集，由于自变量过多，为了防止模型过于复杂及提高模型的精度，采用了基于支持向量回归的遗传算法对变量进行了筛选，结果发现仅用两个铸造涂料的成份（即锆英粉、石墨）就可以实现悬浮率的预测。在此基础上，建立了两个模型：RBF -SVR 模型与BPNN 模型，交叉验证、外部测试验证的结果表明它们都具有很好的预测和外推性能。此外，如果能收集更多的同类型实验数据，模型的精度可以进一步提高。本文使用了多种机器学习方法实现了涂料悬浮率的准确预测，计算方法和过程可以为其它铸造涂料性能预测模型的建立提供有价值的参考。