高性能Ed25519算法硬件架构设计与实现

于 斌 黄 海 刘志伟 赵石磊 那 宁

(哈尔滨理工大学计算机科学与技术学院 哈尔滨 150080)

1 引言

数字签名算法在信息安全领域中具有重要作用，常用的算法有RSA 和椭圆曲线数字签名算法(Elliptic Curve Digital Signature Algorithm,ECDSA)等。在最新的传输层安全性协议1.3版(the Transport Layer Security protocol version 1.3,TLS1.3)中，椭圆曲线算法被收录为基本算法[1]，其中爱德华兹曲线数字签名算法(Edwards-curve Digital Signature Algorithm, EdDSA)作为主要的数字签名算法之一，受到研究者的广泛关注。

Curve25519曲线最初由Bernstein提出，用于密钥交换时称为X25519[2]，其Edwards曲线形式用于数字签名算法，称为Ed25519，与另一同类曲线算法Ed448一起被收入到TLS1.3中，成为重要的签名算法。业界对相关算法做了大量研究，如Faz-Hernández等人[3]使用矢量指令的方式使计算机执行E d 2 5 5 1 9 的速度得到大幅提升；I s l a m 等人[4]在P-256的曲线上兼容了Ed25519的计算，使其具有更好的通用性；戴紫彬等人[5]改善了架构，使密码处理器能够高效并行；Kim等人[6]讨论了Curve25519和Edwards25519曲线上加法运算的转换效率；Salarifard等人[7]通过快速约简实现模乘并完成了Curve25519曲线上标量乘的设计；Turan等人[8]在可编程门阵列(Field Programmable Gate Array, FPGA)上实现了完整的Ed25519功能；Mehrabi等人[9]做了低功耗低面积的设计，完成了X25519功能并支持ED25519的标量乘运算；魏伟等人[10]研究了椭圆曲线密钥交换协议的比特安全问题；在低延迟、侧信道保护方面的研究也有诸多进展[11–13]。

上述各类研究多使用在物联网(Internet of Things, IoT)设备中，偏重于轻量级设计，对签名和验签速度无特别要求。但在特定应用领域，如服务器端，每秒内需要进行大量的签名验签，运算量巨大，现有算法难以满足应用需求。针对这个问题，本文设计了一种高性能Ed25519算法的硬件实现架构，并在TSMC的55 nm互补金属氧化物半导体(Complementary Metal OxideSemiconducto,CMOS)工艺下完成了硬件实现。首先分析了完整的Ed25519算法，划分关键的运算单元；其次对其中的标量乘单元、模L单元和解压单元进行了设计，并充分考虑复用以减小硬件开销，采用速度较快的模约简方式实现模乘，配合此模乘结构调整了点加倍点操作步骤，并使用窗口法完成了标量乘功能；然后利用已有的模乘结构完成模L单元和解压单元；最后实现完整设计并进行性能分析。仿真结果表明，所设计的Ed25519算法硬件实现架构具有速度高、硬件使用率高、计算周期少等优点。

2 Ed25519算法介绍

Ed25519是椭圆曲线签名算法的一种，选用的曲线为Edwards25519曲线，方程为

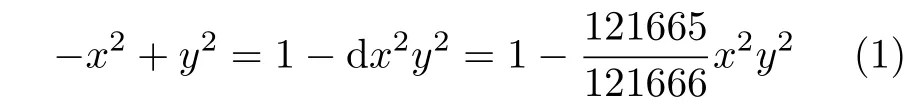
在EdDSA的标准中，共描述了公钥生成、签名和验签3个功能的算法[14]。按其工作过程，首先需进行公钥生成，如表1所示。

表1 Ed25519公钥生成算法流程

由公钥生成算法流程可以看出，运算部分主要是1次SHA-512和1次对椭圆曲线基点B的标量乘。最后的压缩过程实际是保留y的全部信息和x的末位信息，组合成为256 bit公钥。

当有待签名消息M时，需进行的签名过程如表2所示。模操作中的参数L与参数p一样，均为椭圆曲线的固定参数。签名算法的运算部分主要是2次SHA-512、1次标量乘以及对L的模乘和约简运算。

当接收方获得消息M及签名结果R||S，结合发送方的公钥pk，可进行验签操作，具体过程如表3所示。验签过程的解压操作是表1和表2中压缩操作的逆运算，根据压缩结果来计算x的原值。验签算法的运算主要来自2次解压操作、1次SHA-512、2次标量乘和1次点加运算。

表2 Ed25519签名算法流程

表3 Ed25519验签算法流程

3 高速ED25519算法及硬件架构设计

根据Ed25519算法的工作流程，其硬件实现架构设计如图1所示。在整个架构中，SHA-512的设计目前已相对成熟，故不作重点讨论，本文主要针对运算量大的标量乘、模L和解压3部分进行研究和设计，包括标量乘中的点加倍点和模运算等具体操作。

标量乘单元由标量乘控制、乘法器、模约简单元、模逆和模加减构成。其中标量乘控制完成了标量乘算法及点加倍点算法的控制，但仅是对数据的选择控制和部分临时数据的暂存，最终的实现依托模运算，而乘法器和模约简单元配合完成模乘运算。模L单元由模L控制、模加减、乘法器和模约简单元构成，解压单元由解压控制、模加减、乘法器和模约简单元构成，由于标量乘、模L和解压是串行运算关系，故复用了模加减、乘法器和模约简。图1中的SHA-512使用通用结构[15]，乘法器使用单元库中现有结构以保证性能，此两部分不做单独设计。最终，Ed25519控制调用各部分实现公钥生成、签名和验签功能。

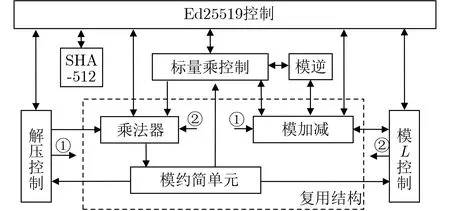
图1 Ed25519完整结构图

3.1 标量乘单元设计

标量乘单元性能的优劣是整个Ed25519的直接体现，完整的标量乘运算分为标量乘算法、点加倍点算法和模运算算法3个层次，标量乘调用点加倍点来实现，而点加倍点调用模运算完成。为了提高签名验签速度，在最底层的模运算中采用快速模约简的方式来设计模乘，点加倍点也需随之调整操作流程，最顶层的标量乘算法采用窗口法来实现。

3.1.1 标量乘算法

本设计中标量乘算法采用窗口法[16]，窗口宽度为2 bit，并针对Ed25519验签进行了设计，增加了1次点加操作，如表4所示。

表4 宽度为2的窗口法

并未采用较热门的非相邻形式(Non-Adjacent Form, NAF)算法，是因为整个系统中有统一时钟，采用NAF算法需对k进行预处理，会消耗额外周期而导致标量乘的总周期数增加，宽度为2 bit的窗口法比NAF算法额外计算11次点加和1次倍点，需要108个周期数完成(详见3.1.2节)，小于NAF算法预计算k所需的平均周期数128个。窗口大小若继续增加，虽会带来总周期数的减少，但会导致存储单元数量的指数增加，预计算所需周期数也会同样增多，故本文最终选定窗口大小为2 bit。

3.1.2 点加倍点算法

点加和倍点运算在标准文档中给出了计算步骤，为得到更好的性能，将2元射影坐标(x, y)转换为4元扩展齐次坐标(X, Y, Z, T)，转换公式为

点加和倍点计算按表5的步骤完成，左侧完成点加，右侧完成倍点，其中d与式(1)中相同，等式左侧均为计算中涉及的临时变量或输出结果。

由于底层的模乘采用模约简来实现，乘法结果需等待一个周期约简后才能再次相乘，考虑到乘法器的使用效率，把表5的操作流程做重新排布，表6是排布后倍点的操作流程，点加也按同样考虑，排布为表7所示操作流程。

表5 点加和倍点操作流程[14]

表6 倍点操作流程

表4窗口法的预计算中2P1按倍点操作，4倍点则执行两次倍点，所以循环过程按“倍点→倍点→点加”的顺序来进行，表6中的步骤(7)，(8)能与表7中的步骤(1)，(2)同时完成，还可以和表6中的步骤(1)，(2)同时完成，两种运算最后的等待约简步骤也可以与下一运算的初始步骤同时运行，即倍点和点加无论如何搭配工作，乘法器均可连续工作，整个标量乘循环只有在结束时等待约简1次即可，乘法器的使用率近似达到百分之百。按此计算，1次“倍点→倍点→点加”实际只需25个周期，无点加时1次“倍点→倍点”实际只需16个周期。

3.1.3 模运算算法

模运算包含模加减、模乘和模逆。为保证表6和表7中的操作可以执行，需正常的模加和模减单元各1个。由于模乘设计采用快速模约简的方式实现，考虑到乘法器延迟较大，在模约简单元输出端连接1个模加和1个模减单元，可以在1个周期内对模约简的结果多做1次模加减操作。此外模逆也需要复用模加和模减单元来简单完成，整个模运算部分的结构如图2所示。

图2 模运算单元

表7 点加操作流程

计算标量乘只需255 bit乘法，但模L运算需要计算257 bit乘法，故选用单元库中的257 bit乘法器，可同时满足标量乘和模L运算需求。模约简公式通常可以根据模数特点利用多项式来推导[17]。在Ed25519中，参数p＝2255–19＝2255–24–22+1，位宽为255 bit，乘法结果A的位宽为510 bit，根据p值的形式特点，设A＝A254·2508+A253·2506+···+A1·22+A0,Ai的宽度为2 bit。其中低256 bit即A127·2254+···+A0，设为T；高254 bit即A254·2508+···+A128·2256做两轮多项式除法，第1轮后得到剩余项A254·2257+(A253+A254)2255+ (A252+A253–A254)2253+(A251+A252–A253)2251+···+(A128+A129–A130)25+(A128–A129)23+(–A128)21，第2轮消去A254·2257+(A253+A254)2255，得到新增剩余项A254·26+(A253+2A254)24+A25322–(A253+A254)，把各部分重新整理后，可得表8所示的快速模约简算法。其中T值是256 bit，Si和Di是255 bit，最后一步待约简的9个和差结果的范围在–2p～5p内，然后接入一个加减法阵列计算出所有可能，并根据标志位来选择正确的输出，整个模约简结构如图3所示。

表8 Ed25519快速约简算法

图3中额外增加了选择信号来选择输入参数是L或p，以及增加了+3q的输出，这两处是为了在模L约简过程中使用，由于模L时不会同时进行模p，可以最大限度复用硬件资源，模L约简算法及设计见3.2节。

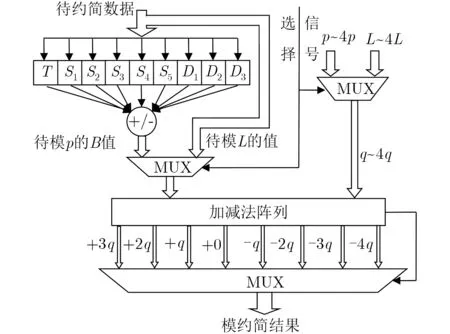
图3 模约简整体结构

模逆只在从4元坐标转换为2元坐标时使用1次，采用二进制右移算法[18]，至多512个周期即可完成运算，每次循环向右移位1次，并做除2操作，可用模加完成。

以上各部分按层次调用，即可完成标量乘运算。

3.2 模L单元的硬件设计

模L运算中的L值形式复杂，不适合做快速约简；且L为253 bit，待约简数值最大为512 bit，异于常规约简的2倍位宽形式；同时考虑到模L运算使用次数较少，单独设计会造成资源闲置；综合以上几点，对比较常用的Barrett约简[19]做改进，复用已有的257 bit乘法器，得到基于Barrett约简的模L算法如表9所示，其中“[ ]”为取整操作。

表9 基于Barrett约简的模L算法

原Barrett约简是对256 bit做模约简，在步骤4中判断输出结果是否大于模数，并进行修正。由于L是253 bit，将L扩大8倍，变为256 bit 8L，采用Barrett约简会得到一个范围在0～8L的值，减去3L后送入图3所示的模约简单元，复用该单元便可得到最终结果，所以直接在步骤(4)中把修正的数值改为减11L和减3L。此方法只需将乘法器扩展2 bit、模约简单元增加少量结构、模减单元扩展1 bit以及额外增加部分控制逻辑即可实现模L约简。

3.3 解压单元的硬件设计

解压的目的是根据坐标x值的最后一位和坐标y值，来计算x的完整坐标值，计算公式为

解压运算采用标准中推荐的算法来实现[14]，需计算

再对t进行判断和修正即可，主要计算量集中在模幂操作，由于参数p固定，可得

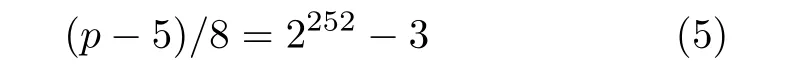
根据其形式特点，复用快速模约简的模乘结构，为达到乘法器的最高使用率，设计了如图4的模幂操作步骤图，其中的b＝uv7，是模幂的底数。按此操作步骤运行，完成b的(2252–3)次模幂只需506个周期。

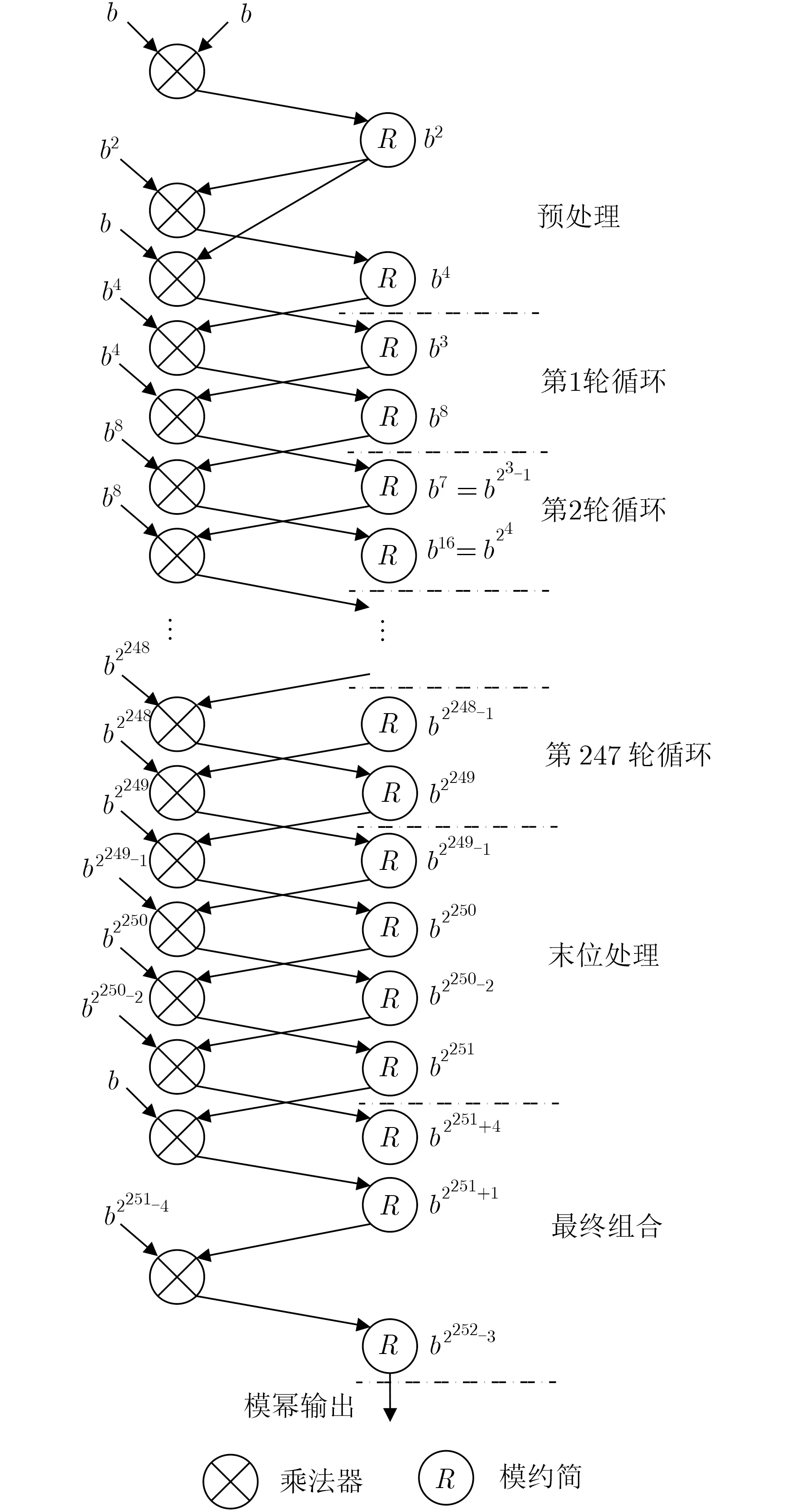
图4 b的2252–3次模幂操作步骤图

4 硬件实现与性能分析

最终设计采用55 nmCMOS工艺库进行综合，可得表10和表11所示的性能参数结果。整个设计能够工作在360 MHz主频下，约占用746×103个等效门，平均每秒可以运行11.12×104次的公钥生成、10.76×104次的签名和4.81×104次的验签，即使对于极端特殊的情况，理论上也能达到每秒9.06×104次的公钥生成、8.82×104次的签名和3.99×104次的验签。由于未设置额外存储器，1次待签名信息需小于512 bit。

表10 Ed25519性能参数

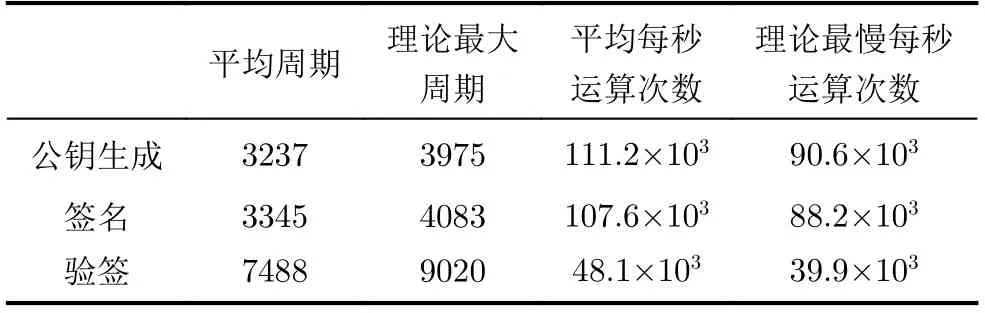
表11 周期及运算次数

由于Ed25519的实现多用于IoT设备，习惯基于短位宽乘法的迭代来设计，而FPGA中的DSP单元可以更灵活地提供乘法性能，故已知研究常在FPGA上进行。文献[8]在FPGA上完成了Ed25519的全过程，其优化算法每秒分别可以计算474次的公钥生成、621次的签名和272次验签，表12使用的是文献[8]中每个功能所需的平均时间。

完整的Ed25519硬件实现很少，为了进一步评估性能，用Xilinx的Zynq-7035对本设计的标量乘做简单约束实现，并给出表13的对比结果。本设计中并未投入精力对257 bit乘法器做进一步时序优化，用以在FPGA上达到较高工作频率，所以使用了周期数来衡量运算速度，用消耗的Slices和Cycles的乘积再乘以10–6得到的结果值做性能对比的参考，其中文献[9]未给出Slices参数，使用LUT/4来近似计算。

由表13可以看出，文献[8]的标量乘使用了15个DSP做循环迭代来计算256 bit模乘，这样消耗的硬件资源很少，对于IoT设备是较好的选择，但需要消耗很多周期。最终使用该标量乘来完成的Ed25519，在其执行速度上也如表12所列一样，并未有太多竞争性。文献[9]采用基8的循环移位模乘，所以没有DSP单元的消耗，但整体性能稍差。文献[11]使用快速模约简，分为高128 bit和低128 bit来进行模乘，所以所需周期数是所有文献中最少的，同样，硬件资源的消耗情况也是所有文献中最大的。文献[12,13]也是使用FPGA中的DSP单元按17 bit分段进行模乘，只是迭代过程各有区别。与上述文献相比，本设计中标量乘的整体性能可提高约10%，具备一定的优势，而标量乘是整个Ed25519的核心单元，也能从一定层面上反映整体的性能。

表12 Ed25519运算速度对比(μs)

表13 标量乘单元性能对比

5 结论

本文对椭圆曲线签名算法中的Ed25519算法进行了研究，使用快速模约简计算模乘，并据此完成了点加倍点操作步骤的重新排布，然后使用窗口法实现了标量乘运算。设计中改进Barrett约简用于模L的实现，还为解压算法设计模幂的操作步骤，充分复用已有单元，在保证运算速度的前提下，尽可能地减小硬件开销。最后实现的硬件电路能够完成Ed25519的完整操作，相较于其他设计，在运算速度上具有显著优势。