基于CNN扰动的极化码译码算法

赵生妹 徐 鹏 张 南 孔令军*

①(南京邮电大学通信与信息工程学院 南京 210003)

②(中国航天系统科学与工程研究院 北京 100048)

1 引言

极化码是一种基于信道极化理论的信道编码[1]，自Arikan提出以来，引起了广泛的关注[2]，串行抵消(Successive Cancellation, SC)译码算法是Arikan针对极化码的结构提出的极化码独有的译码算法，在SC 算法下，通过严格的数学证明，得到极化码可以在二进制离散无记忆信道(Binary Discrete Memoryless Channel, B-DMC)下进行无差错传输，并且容量可达[3]，与此同时，SC译码算法具有较低的计算复杂度，仅为O(Nlog2N)。然而在实际状况下，码长不可能“足够长”，一旦发生错误的比特判决(比特错误)，由于顺序译码的特性，错误的比特没有机会被纠正[4]。

因此，基于SC译码算法的改进算法成为极化码译码的研究热点，研究者提出了一系列算法来改善极化码的SC译码性能[5]。文献[6]提出了SC翻转(SCF)译码，在SC解码失败(通过CRC校验检测)，则尝试识别并翻转先前译码期间发生的第1位错误，一直尝试直到译码通过CRC校验，或达到最大尝试次数。在文献[7]中，针对SC译码只保留一条译码路径，从而导致正确路径容易丢失的问题，提出了串行抵消列表(Successive Cancellation List,SCL)译码算法，其可保留L条路径。尽管SCL译码具有优越的性能，但是由于保留了L条路径使其计算复杂度高、内存需求大、译码吞吐量低。因此，文献[8]提出了简化的SCL译码算法(Simplified SCL, SSCL)和快速简化的SCL译码算法(Fast Simplified SCL, Fast-SSCL)，虽然它们都能降低计算复杂度，但是性能将有所下降。基于CRC辅助SCL译码算法(CA-SCL)[9]改进的自适应SCL译码算法(ADaptive SCL, AD-SCL)[10,11]，则根据译码序列的CRC校验结果判断是否增大L值重新译码，降低了整体译码复杂度同时获得较好的译码性能，但是在低SNR时重译次数较高。文献[12]提出一种基于分段CRC的自适应SCL译码算法(Segmented-CRC ADaptive SCL, SCAD-SCL)，文献[13]提出了多级CRC辅助校验的SCL译码算法，降低了平均复杂度和时延。

针对极化码SC译码算法性能不佳，且现有性能较好的SCL等改进译码算法复杂度较高的现状，本文从SC配置的次优性和极化码的最小距离[14]进行分析，通过向接收信号添加次级独立随机噪声以改善极化码译码器的性能[15]。传统的SC译码算法通常仅提供一个输出，如果该输出被证明是无效的码字，则声明译码错误。然而，利用扰动算法，可以通过向接收信号添加次级独立噪声来产生其他可能的候选码字。最近深度学习在处理噪声等任务中取得了巨大的进步[16]，因此，本文通过CNN来对接收信号提取噪声特征，根据接收信号在码空间中与有效码字的偏离程度，动态调节扰动噪声的大小(噪声方差)，对添加了扰动噪声的接收信号重新计算似然信息并译码，设计迭代算法，重复该过程直到获得有效的码字或者达到迭代阈值。在复杂度较低的情况下，可提升误码率(Bit Error Ratio, BER)性能。

2 极化码基本原理

由极化码的编码过程可知，极化码的构造就是容量趋于1的比特信道(又称为极化信道)的选择过程，是以最优化SC译码性能为标准的，根据极化信道转移概率函数式，各个极化信道具有确定的依赖关系：信道序号大的极化信道依赖于所有比其序号小的极化信道。基于这种关系，SC译码对比特进行判决时，需要假设之前得到的译码结果都是正确的，正是在这种情况下，极化码被证明了是信道容量可达的。因此对于极化码而言，基于SC的译码算法是最合适的，只有这样才可以充分利用极化码的结构，保证在足够码长时容量可达。

3 基于CNN扰动的极化码译码算法

3.1 扰动噪声译码

在实际通信系统中，噪声是最不期望存在的，因为信道中的噪声会对发送信息产生影响，严重时可造成有效信息在接收机处不能恢复，严重影响通信系统的性能。然而，从译码纠错空间的角度分析，特定的扰动噪声可能会有助于译码，进而提升了译码器的性能。图1为基于码空间的线性码纠错译码示意图，其中M个码字的可纠错区域分别标记为a1, a2, ···, am。若以可纠错区域a2为例，当发送与其对应的码字c2时，接收信号y由于在信道中受到噪声的干扰，落在译码空间中位置可能是随机的。如果错误在可纠正范围内，则其应将落在a2区域内，则根据译码规则可以获得正确估码c2，得到与该码字对应的发送信息。如果落在该a2区域之外，则表明信道噪声对该信号产生了较大的干扰，超出了纠错能力范围，导致译码失败。从图1中可以看出，如果在接收信号中添加次级独立的扰动噪声，那么接收信号y在译码纠错区域内的落点就会发生偏移，有可能会移动到可纠错区域之内。如果译码过程中发生的错误相对较少[17]，那么信道接收信号有可能非常靠近其特定的纠错区域。添加扰动噪声产生的这种有益效果可以用随机共振的现象来进行解释，其定义是向信号中添加随机独立噪声使其增强[18]。

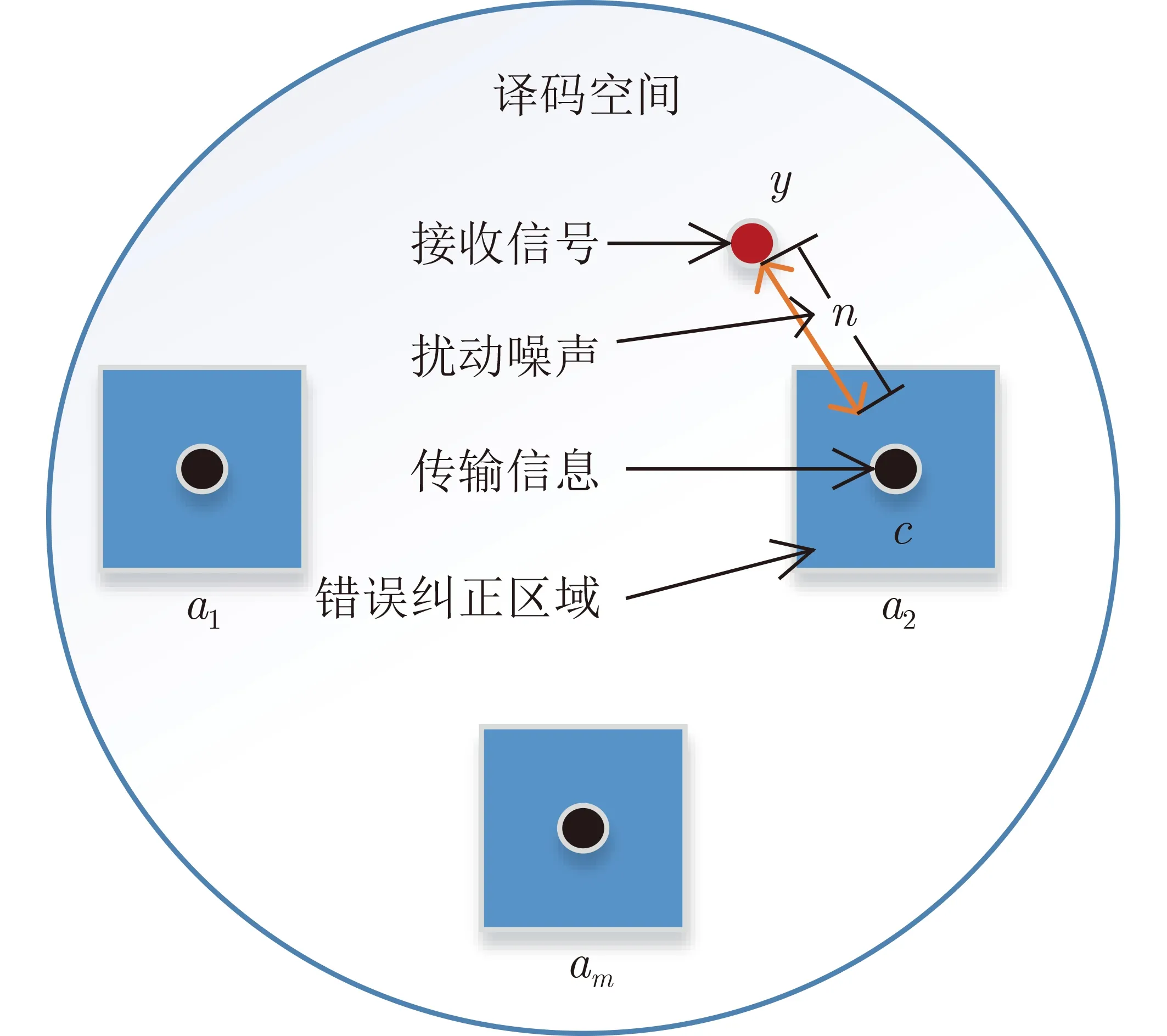
图1 译码空间示意图

然而，若只是添加独立的随机噪声，将使得接收信号的落点在译码空间中较为随机，要使其回到正确可纠错区域内可能需要尝试多次。因此，本文利用卷积神经网络强大的学习能力，从接收信号中提取特征，并根据接收信号与发码间的偏离程度，动态地调节扰动噪声的均值与方差，有效地将接收值y调回到其可译码纠错区间内，通过对添加了扰动噪声的接收信号重新计算似然比并译码，获得有效的译码。

3.2 基于CNN扰动的极化码译码算法

图2是基于CNN扰动噪声的极化码译码流程图，具体算法见表1。首先用SC译码器对信道接收值进行译码，估计值通过式(4)判决得到

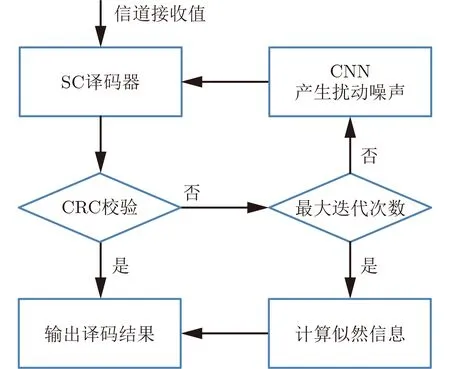
图2 基于CNN扰动噪声的极化码译码流程图

表1 基于CNN扰动噪声译码算法

如果译码结果通过CRC校验则表明译码成功，输出译码结果，如果译码失败则通过CNN对信道接收值提取特征，产生扰动噪声np，将其加到y上，y'＝y+np，且使用y'代替y重新进行SC译码，这里对添加扰动噪声后的接收信号LR进行修正，

其中，x(uˆi)为译码结果序列通过极化码编码与BPSK调制后的向量。然后把最大值L(uˆi)对应的译码结果作为输出。

3.3 神经网络设计与训练

神经网络利用类似于人脑的分层模型结构，从底层到高层对输入数据逐级提取特征，在底层信号到高层语义之间建立起映射关系。本文设计的CNN网络的参数如表2所示。

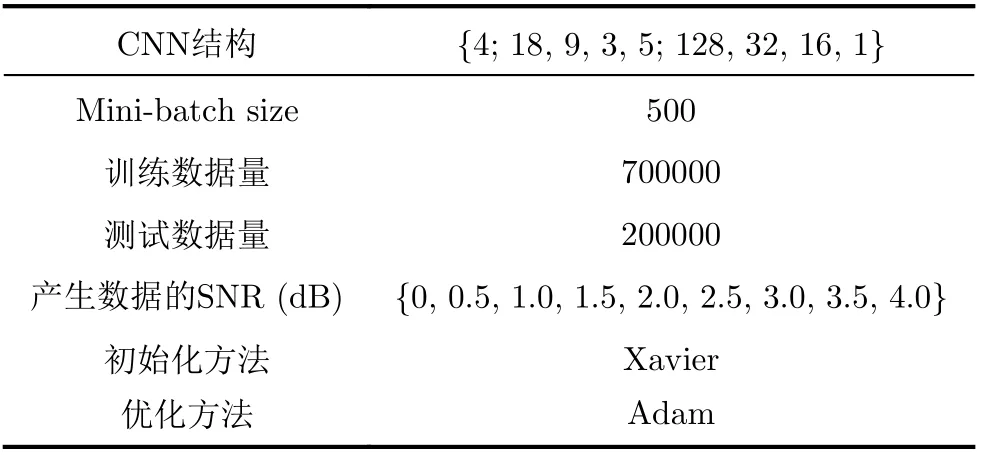
表2 CNN训练相关参数

本文分两个阶段来训练神经网络，由于整个训练过程是离线完成的，所以不会增加译码的复杂度。在这里，根据参考文献[16]中的定义，使用了损失函数的正态性检验，以便测量接收值在译码纠错空间的可能性，便于之后的似然信息的计算。损失函数定义为

其中，n表示真实噪声向量，n'是CNN输出噪声向量，偏度D和峰度K定义为

(1) 进行了大量的模拟，使用极化码编码随机信息比特，然后用SC译码带有噪声的BPSK符号，如果译码结果不通过CRC校验，则表明译码失败，需要加入扰动噪声。在这种情况下，储存一对y以及能够使其回归到译码可纠错区域的扰动噪声(对加入的随机噪声取负)np。

(2) 使用训练数据训练神经网络以最小化损失函数。将数据库分为两组：训练集和验证集。训练集用于训练网络，而验证集用于避免过度拟合。虽然训练质量受某些超参数的影响，但是在本文中，不关注这些超参数的优化，只选择一组有效的超参数。

(3) 考虑到在加入扰动噪声之后译码仍然失败的情况，所以要循环迭代，重复加入扰动噪声，这在第1阶段是未被训练的，所以要进一步训练神经网络，使其在上一次扰动噪声的基础上输出正确的扰动噪声。为了解决这个问题，在第2阶段继续训练CNN，如图3所示。在每次迭代中，基于CNN生成新的数据。然后，使用更新后数据库强化学习来训练神经网络。

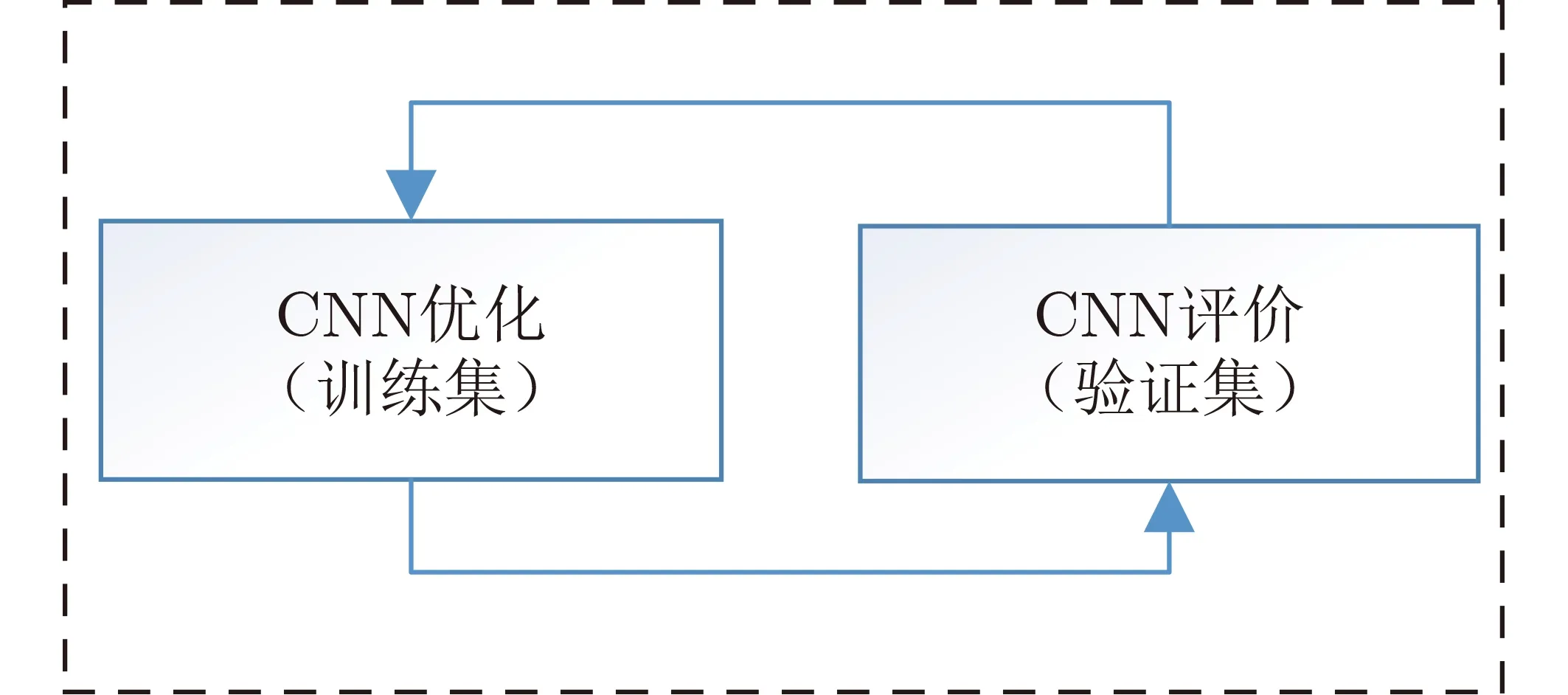
图3 强化学习迭代训练CNN

4 仿真结果分析

本文通过数值仿真来分析基于CNN扰动的极化码译码算法的性能，以验证该算法的有效性。极化码码长N为1024，码率为0.5，信道条件为高斯白噪声信道。图4为不同译码算法的性能比较，从图中可以看出，本文所提出的译码算法与SC译码算法相比可获得约0.6 dB的增益，与添加随机扰动噪声(PA)相比(重译次数门限T为10)，约有0.4 dB的增益。本文的译码算法在低信噪比时与SCL(L＝16)译码算法相比有接近0.1 dB的增益。但是，在信噪比＞2.75时，所提译码算法性能不如SCL(L＝16)译码算法。这是因为当信噪比较高时，噪声较小，可提取的特征也减少，由CNN输出的扰动噪声将接收信号带回可译码区域的能力下降，BER性能下降趋势缓慢。本文认为这可能是由于神经网络的识别能力随着信噪比的提升下降而导致的。因此，针对这种现象，可以采用以下措施：(1)增加CNN网络的训练量，特别是在高噪声比下的训练数据，以提高CNN在高信噪比时对噪声特征的识别能力，进一步提升所提译码算法的BER性能；(2)提高重译的门限次数T，以提升高信噪比下所提算法的BER性能，可获得与SCL(L＝16)结果相当的性能。

图4 不同译码算法性能比较

为了进一步说明基于CNN扰动的Polar译码算法性能，图5显示了基于CNN的扰动译码算法与基于深度神经网络(DNN)的扰动译码算法的性能对比，其中DNN最大迭代次数为10。从图中可以看出，基于CNN的扰动译码算法性能更好，与基于DNN的扰动译码算法相比，性能约有0.4 dB的提升。

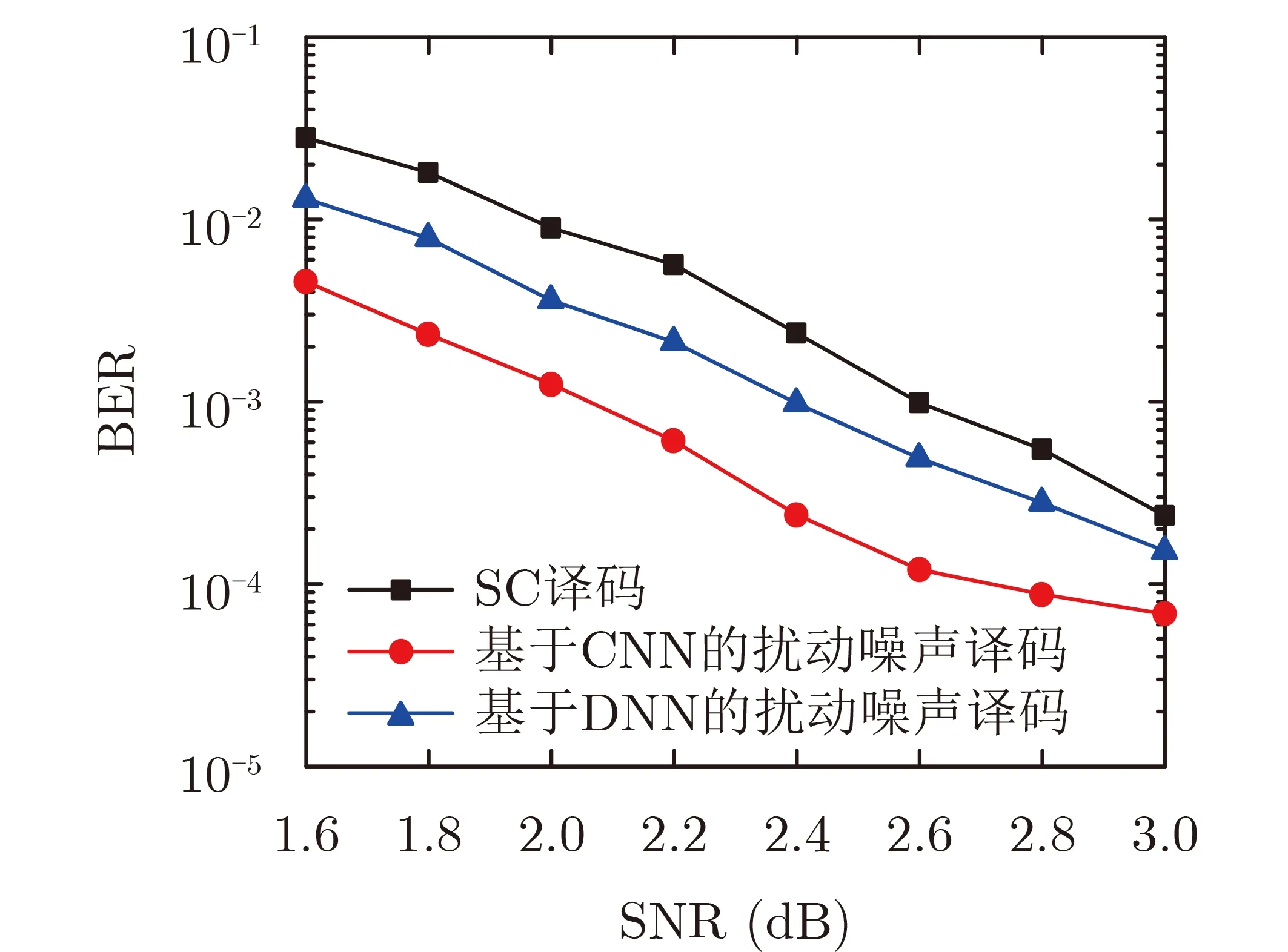
图5 基于不同神经网络的译码算法的性能比较

通过增加迭代的次数来进一步降低BER，图6为不同最大迭代次数下的BER性能，从图中可以看出，只设置1次迭代已经有相当不错的性能，说明CNN已经可以产生较为满意的扰动噪声，随着最大迭代次数的增加，性能逐渐增加，但是增益缓慢。考虑到译码复杂度，当T＝10时，译码效果最佳，有着较好的BER性能和较低的计算复杂度。

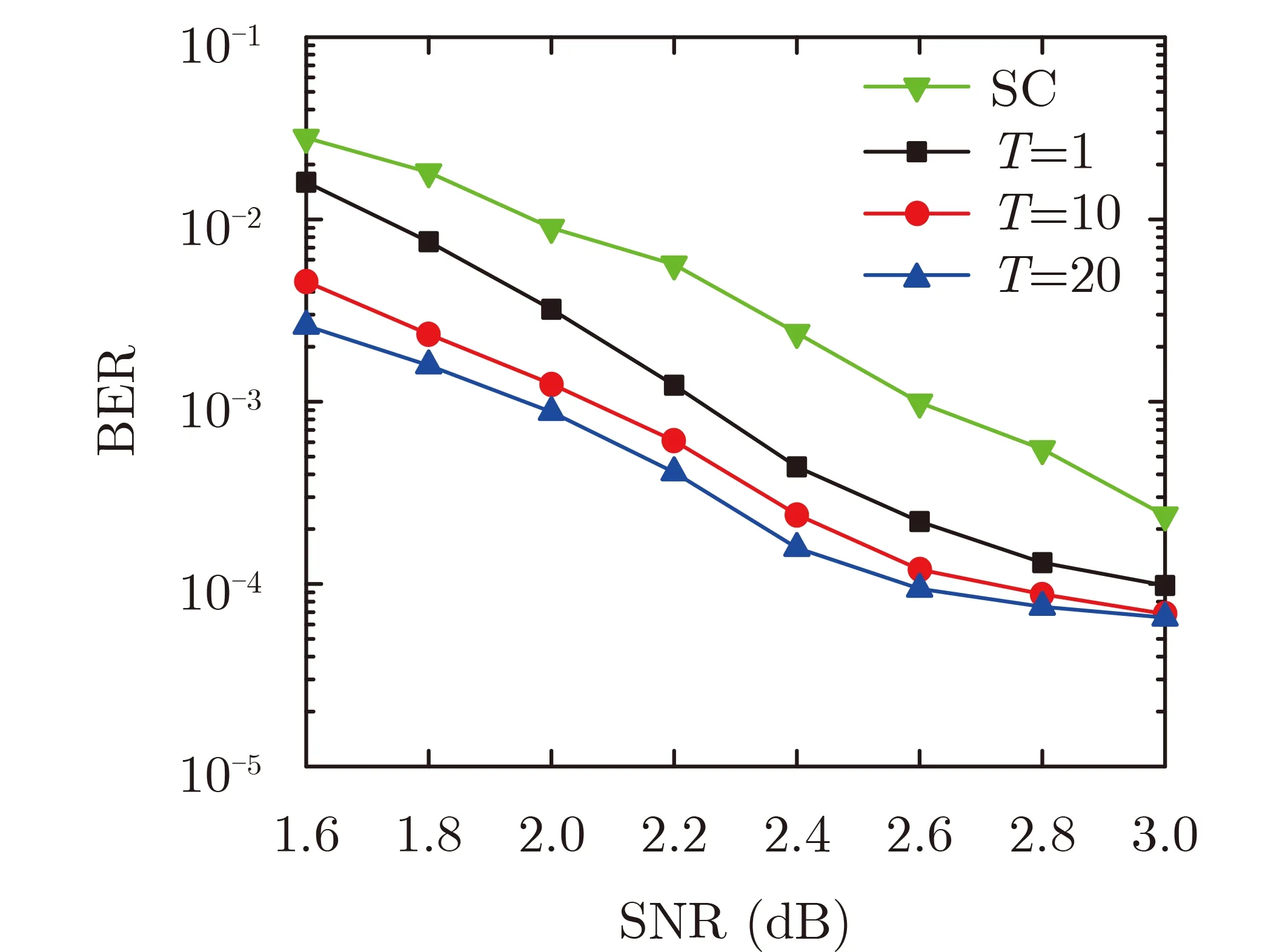
图6 不同最大迭代次数下译码性能对比

与传统SC算法相比，本文所提译码算法具有更多计算，因而复杂度较高。但是由于仅在SC译码失败时才需要后续的计算，所以平均来说译码复杂度不高。图7为不同译码算法的平均SC译码次数，从图中可以看出，SC与SCL的译码次数是不随着信噪比的增加而变化的，本文提出的译码算法只针对译码失败的序列进行迭代，所以当信噪比提高时，发生译码失败的概率减小，所以译码复杂度和SC译码算法相比几乎相同。

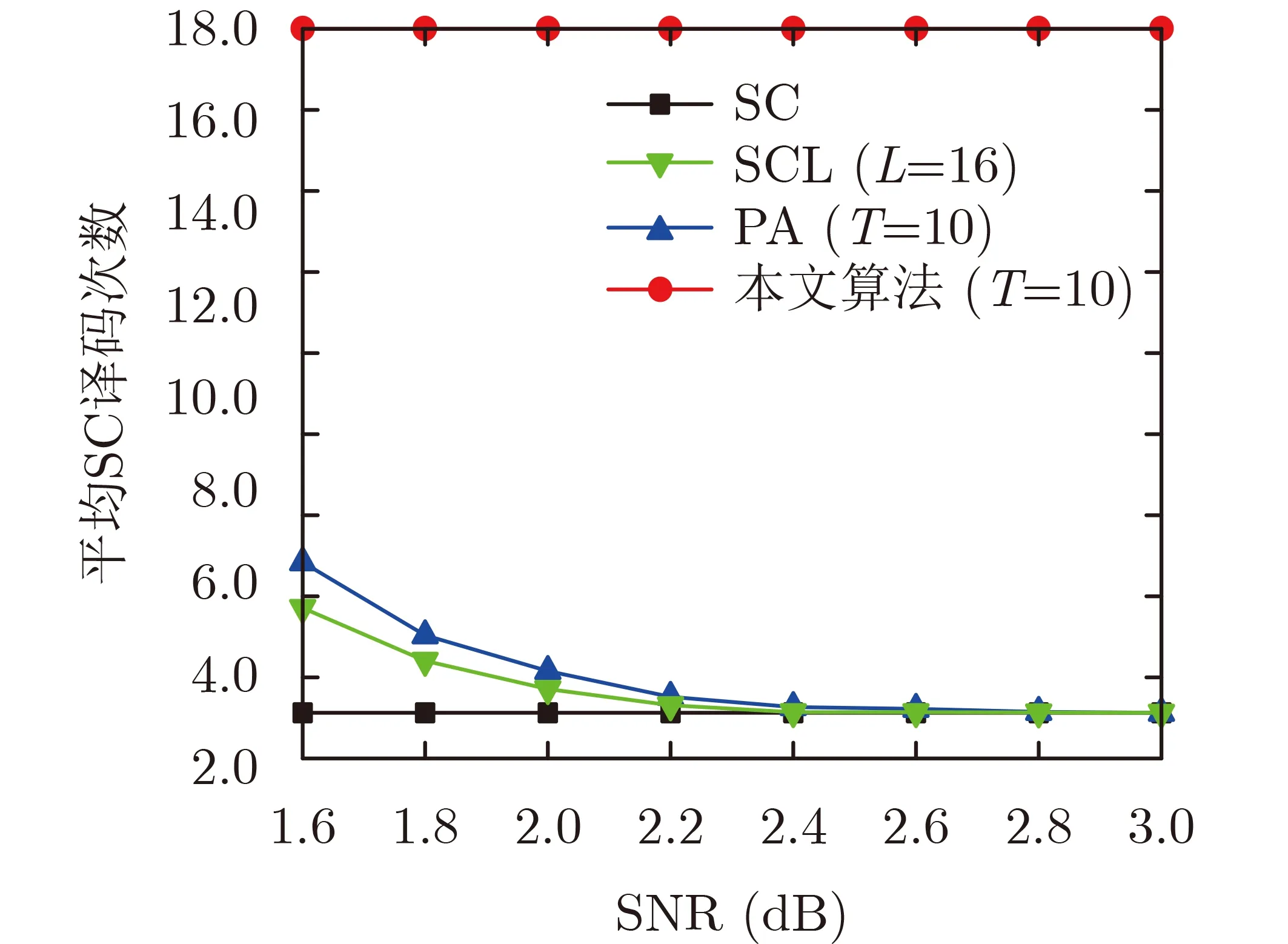
图7 不同译码算法的平均SC译码次数

5 结束语

为了提升SC译码的性能，本文采用译码后处理技术，针对码空间译码可纠错区域的特点，通过CNN产生特定的扰动噪声，使译码失败的接收信号重新落在可纠错区域之内，有效地提升了极化码的SC译码算法的性能。仿真结果表明，在同等条件下，本文提出的算法与SC算法相比在复杂度较低的前提下具有更加优异的性能，与SCL(L＝16)译码算法相比，在译码性能相当的前提下有效地降低了译码时延。此外，本文以SC为例给出了基于CNN扰动噪声译码方法，该思想也可以推广到极化码的其他译码算法或其他信道编码的译码算法之中[19,20]。