电动汽车锂离子电池荷电状态估算方法研究综述

张照娓 郭天滋 高明裕* 何志伟 董哲康

①(杭州电子科技大学电子信息学院 杭州 310018)

②(浙江省装备电子研究重点实验室 杭州 310018)

③(香港理工大学电机工程系 香港 999077)

1 引言

随着全球变暖、各种极端气候的出现，柴油、汽油车造成的温室气体排放问题越来越被重视，为了减少城市污染，电动汽车和混合动力汽车的发展受到了广泛关注。为了确保电动汽车的运行安全性、耐久性、可靠性和效率，执行必要的管理和诊断功能，电池管理系统(Battery Management System, BMS)被广泛应用于电动汽车中[1]。荷电状态(State of Charge, SoC)表示电池的剩余可用电量，是BMS需要监测的重要的状态之一，它提供有关电池中剩余的可用能量及其潜在充电和放电策略的可靠性信息[2]。

传统的SoC估算算法有放电测试法、阻抗谱法、安时积分法、开路电压法等，但这些方法估计误差较大且无法进行实时估计。因此近年来基于模型的滤波估计方法和基于数据驱动的方法得到了广泛的关注与研究。基于模型的滤波估计方法是对电池建模，利用电池模型来模拟电池行为。随着计算机技术的发展和大数据时代的到来，基于数据的人工智能算法得到了迅速的发展[3]，它不需要对电池进行建模，依靠大量的数据训练模型，以建立电池可测量因素与SoC的对应关系。

为了推动锂离子电池SoC估计算法的发展，近年来，一些学者对目前常用的SoC估算算法进行了分析与总结。文献[4]对电池的SoC估计方法进行了综述，主要介绍了3种电池模型以及基于模型的估算方法，但是基于数据驱动的方法并没有得到具体的介绍。文献[5]对锂离子电池的SoC估计方法进行了深入的文献综述，重点讨论了估计误差、优点和缺点。但是没有提供SoC算法实现的任何数学表示、流程图以及框图。文献[6]分析了5种误差源对基于模型的SoC观测器的影响，并实现了理论与仿真。文献[7]将SoC估计方法分为经典的估计方法和智能算法两类，讨论了算法的执行过程和优缺点。本文简要分析了锂离子电池特性和影响电池SoC估计因素，通过总结最新的研究成果，综述了近年来电池SoC估算方法及其优缺点，并对未来的研究方向进行了展望。

2 锂离子电池和SoC

2.1 锂离子电池

锂离子电池于1976年被提出，1979年Goodenough教授在牛津大学证明了锂钴氧化物可以用来制造一种能够储存能量的可充电电池，索尼公司于1991年将第一块锂离子电池商业化[8]。相较于其他类型电池，锂离子电池具有能量质量比高、循环性能好、自放电率低、无记忆效应等优点，并且其快速充电能力强，在电动汽车以及混合动力汽车中得到了广泛的应用。

以磷酸铁锂电池为例，其工作原理如图1所示，电池的充放电过程就是锂离子嵌入和脱嵌过程。在充电过程中，正极材料失去电子，锂离子在电场力的作用下从正极穿过电解液和隔膜，到达负极嵌入到石墨层中，同时电子通过外电路到达负极，使负极的电荷达至平衡。在放电过程中，电子从负极材料流出，失去电子的锂离子也从石墨层间脱嵌而出，从负极脱嵌后的锂离子再次通过电解液及隔膜回到正极材料，电子通过外电路流向正极，使正极的电荷达至平衡。电化学反应方程式可表示为

图1 锂离子电池工作原理示意图

2.2 电池SoC

SoC反映电池的剩余电量，通常使用美国先进电池联合会(United States Advanced Battery Consortium, USABC)给出的定义，即在特定放电倍率的条件下，电池剩余电量占额定容量的百分比

其中，S为电池的SoC, QC为电池当前电量，QI为电池的额定容量。S的取值范围为0～1，当S＝0时表示电池完全放电，S＝1表示电池完全充满。SoC提供了有关电池中剩余的可用能量以及电池潜在充放电策略的可靠性的信息。准确了解电池的剩余电量，可以有效避免过充过放现象，对电池健康状态评估，提高电池使用寿命，保障行驶安全有着重要的意义[9]。

锂离子电池作为高度复杂的非线性系统，SoC无法直接测量得到，只能通过电池端电压、充放电电流及内阻等参数来对其进行估算。然而这些参数还会受到电池老化、环境温度变化及汽车行驶状态等多种不确定因素的影响，同时电池的额定容量也在不断发生变化。对于电动汽车而言，复杂的地形和路况带来了复杂的功率输出，而能量反馈则进一步增加了估算难度，因此如何准确估计锂离子电池的SoC已成为电动汽车发展中亟待解决的问题[10]。

3 SoC估算方法

通过总结最近发表的有关SoC估算方法的文献，本文将各类算法归为5类，分别为查表法、安时积分法、基于模型的估算方法、基于数据的估算方法和混合方法，如图2所示。本节将对这5类方法分别做出简要概述。

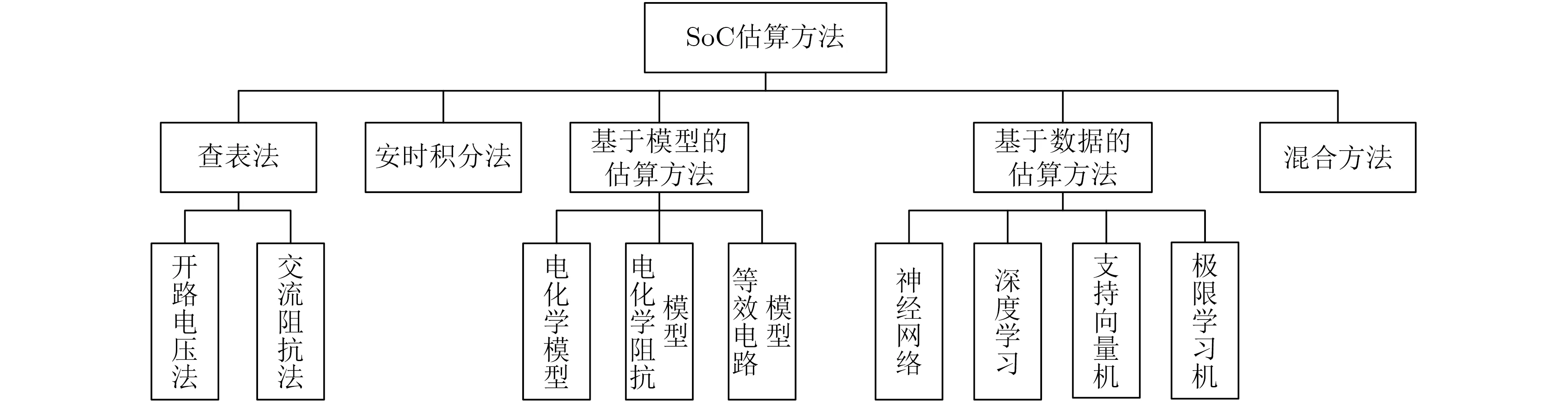
图2 锂离子电池SoC估算方法分类

3.1 查表法

查表法利用了电池外部特性参数与SoC之间的映射关系，通过实验来表征电池行为，将电池参数与SoC的关系列表化。目前常用的查表法有两种，一种是开路电压 (Open Circuit Voltage, OCV)法[11]，另一种是交流阻抗法[12]。

3.1.1 开路电压法

电池的OCV在数值上接近电池电动势，且与内部锂离子浓度之间存在一定的映射关系，通过大量密集的实验建立OCV-SoC查找表，当电池处于工作状态时，通过测量电池的OCV，根据OCV与SoC之间的映射关系估计电池的SoC[13]。需要指出的是，由于电池内部欧姆电阻、极化电阻、电化学极化和浓度极化产生的磁滞现象，需要静置使电池内部的电解质均匀分布以获得稳定的端电压[14]。另外，通过放电实验建立的OCV-SoC查找表，只适用于相同实验条件的电池估计，当目标电池处于不同温度、不同生命周期时，再利用之前建立的查找表计算SoC误差将会变大。在放电过程中期，OCVSoC曲线变化非常平坦，SoC估计变得非常敏感，在这种情况下，较小的OCV误差会导致较大的SoC估计误差[15]。

3.1.2 交流阻抗法

交流阻抗法是查表法类别下的另一种方法，电池的交流内阻与电池SoC有着密切的关系，通过电化学阻抗分析仪来测量电池的交流阻抗，来建立阻抗查找表。与OCV法类似，在测量锂离子电池的交流阻抗之前，需要将电池静止一段时间以达到稳定状态。然而，在电池SoC较大时，其阻抗变化不明显，而当电池的SoC下降到一定水平时，阻抗会迅速上升，并且电池的交流阻抗受到温度的影响很大。

3.2 安时积分法

安时积分法，又称作电流积分法，是目前应用最广泛的锂离子电池SoC估计方法之一[16,17]，其主要思想是测量电池的放电电流并将电流随时间进行积分来计算一段时间内放出的电量，进而估计电池的SoC[18]。安时积分法计算公式为

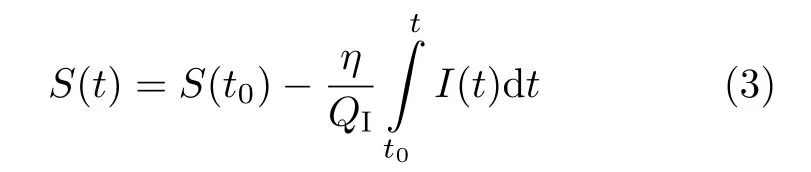
式中，S(t0)为初始荷电状态，η表示库仑效率，I(t)为电池的瞬时放电电流。通过对放电电流进行积分得到电池在t～t0这段时间放出的电量，用初始荷电状态减去放出电量即为当前时刻电池的荷电状态。

安时积分法是一种相对简单的可以进行电池SoC在线估计的方法，在估算的过程中，只需要关注系统中流入和流出电量以及电池的初始荷电状态，具有简单性和稳定性，易于应用在低功耗电池管理系统中[19]。但是安时积分法更适合用于放电电流比较稳定的情况，在实际应用中，电动汽车在行驶的状态下电池的放电电流很难达到持续稳定的状态。

3.3 基于模型的估算方法

3.3.1 电池模型

(1) 电化学模型(Electrochemical Model, EM)。EM根据电化学反应过程计算电池的端电压和SoC，是一种基于多孔电极和溶液浓度理论的电池模型[20]。P2D模型使用一组耦合偏微分方程描述了锂离子电池固相锂离子浓度和电势，是一种在锂离子电池SoC估计中应用最广泛的EM[21]。电化学模型主要反映电池内部化学反应机理，模型准确度高，但是很难确定所有的参数，具有巨大的计算复杂度和耗时性[22]。

(2) 电化学阻抗模型(Electrochemical Impedance Model, EIM)。电化学阻抗谱(Electrochemical Impedance Spectroscopy, EIS)是Heaviside在1894年提出的一种电池测量技术，常用来建立电化学阻抗电路模型[23,24]。EIM采用EIS的方法获得在频域范围内的交流等效阻抗模型，通过EIS测定等效电路的构成以及各元件的大小，然后使用一个复杂的等效网络来匹配阻抗谱，EIM可以准确描述电池特性，但在实际应用中匹配过程难度大、复杂并且不直观，并且阻抗模型只有在特定的SoC和温度有用，无法预测直流反应及电池运行时间[25]。

(3) 等效电路模型(Equivalent Circuit Model,ECM)。ECM用来描述和模拟电池的动态特性，它将电池看作一个二端口网络，用电压源、电阻、电容等器件组成电路，来模拟电池内部特性[26,27]。目前已经提出各种ECM模型用于锂离子电池的SoC估计，常见的有Rint模型[28]、Thevenin模型[29]、2阶电阻电容并联等效模型[30]、新一代汽车的合作伙伴关系(Partnership for a New Generation of Vehicle,PNGV)模型[31]等，如表1所示。

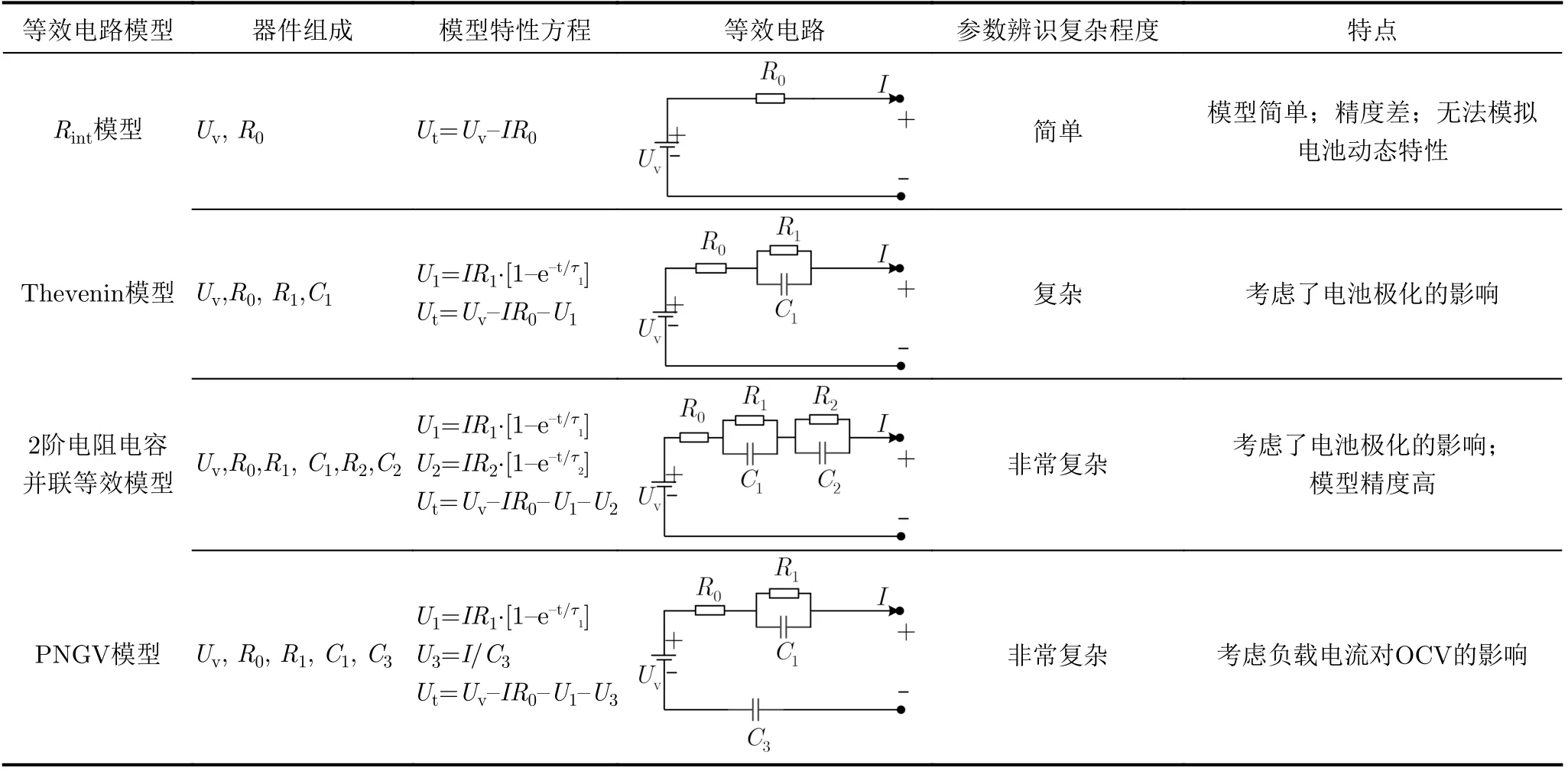
表1 4种常用等效电路模型

另外还有改进PNGV模型[32]、分数阶模型[33]等，改进的模型拟合出的曲线与真实电压曲线匹配度更高，但是电路模型也变得更复杂，参数的增加使得参数辨识更难实现。ECM结构简洁，便于计算，研究人员常将ECM与诸如卡尔曼滤波器之类的自适应算法相结合进行电池SoC估算[34]。

3.3.2 基于模型的非线性观测器

为了实现动态SoC估计，常将非线性观测器与电池模型相结合，构成基于模型的SoC估算方法。基于模型的估算方法使用闭环结构，能够对初始状态未知的电池SoC进行估计，估算方法结构如图3所示。该方法可以使用不同的算法来计算增益，例如卡尔曼滤波器及其变体[35–38]，粒子滤波器(Particle Filter, PF)[39,40]，H无穷滤波器(H Infinity Filter,HIF)[41–44]，以及其他状态观测器类如比例积分观测器(Proportional-Integral Observer, PIO)[45,46]，滑模观测器(Sliding-Mode Observer, SMO)[47,48], Luenberger观测器(Luenberger Observer, LO)[49,50]等。

图3 基于模型的锂离子电池SoC估计方法结构图

(1) 扩展卡尔曼滤波器(Extended Kalman Filter,EKF)。卡尔曼滤波器(Kalman Filter, KF)是一种用于动态线性系统状态估计的最优递推估计方法，其基本思想是将测量的端电压与建模的端电压进行比较，并通过一个增益矩阵将差值反馈给SoC的预测值。由于KF仅适用于线性系统，在非线性系统中的估计性能较弱，因此学者们常常将KF的两个扩展方法EKF和无迹卡尔曼滤波器(Unscented Kalman Filter, UKF)，应用于锂离子电池SoC的估计来处理非线性问题[51,52]。EKF在每一个时间步采用一个线性化过程，通过1阶泰勒级数展开来逼近非线性系统。

为了提高EKF对电池ECM非线性区域的估计性能，文献[53]通过Lyapunov稳定性分析设计了在线参数观测器对电池内部参数进行辨识，再对卡尔曼过程进行重新建模。为了降低计算成本，文献[54]提出了一种基于勒贝格采样(Lebesgue Sampling,LS)的LS-EKF估计SoC的方法，LS通过“仅在必要时”执行，能够消除不必要的计算。

(2) 无迹卡尔曼滤波器(UKF)。EKF通过1阶泰勒级数展开来逼近非线性系统，仅达到1阶精度，并且1阶近似可能导致噪声的后验均值和协方差误差较大。为了克服泰勒级数展开算法的不足，文献[51]提出了基于无迹变换的UKF方法。UKF通过引入加权sigma点的概念来解决EKF的近似问题，采用预先确定的采样点对系统进行采样，理论分析证明其估计精度明显优于EKF[55]。

为了减少外部因素对系统估计精度的影响，研究学者们对UKF算法进行了改进。基于UKF算法，文献[56]提出一种改进的噪声抑制算法来估计电池的SoC，对卡尔曼滤波器增益和估计的残差进行校正以增强滤波效果，同时加入了无效值消除算法以提高其稳定性。文献[57]提出了一种基于自协方差最小二乘(Autocovariance Least-Squares, ALS)技术的改进UKF算法来实现对电池SoC的估计，ALS与UKF结合可以在提高收敛速度的同时得到更高精度的SoC估计。近年来学者们还将许多改进的UKF算法应用到了SoC估计中，如自适应无迹卡尔曼滤波[58]、平方根球形无迹卡尔曼滤波[42]等。

(3) 粒子滤波器(PF)。EKF和UKF算法要求系统噪声为高斯分布，对于非高斯系统噪声，通常使用基于概率分布理论的PF来处理。在实际应用中，有必要考虑简并或样品贫化问题，因为在这种情况下，少数粒子几乎占了全部权重，当有效粒子Neff的数量低于一定的阈值NT时，通常通过重采样来避免这种现象。

PF在实际应用中同样存在一定的局限性。针对PF算法中的简并性，文献[59]利用人工免疫算法对PF进行优化，优化后的人工免疫粒子滤波算法能更好地满足真实变化曲线。针对PF算法中的粒子贫化问题，文献[60]考虑到PF对噪声的敏感性，提出了一种自适应加权容积粒子滤波器估计SoC的方法，在自适应加权估计的基础上调整容积点的权值，抑制了系统噪声对状态估计的干扰。此外，UKF和PF结合形成的无迹粒子滤波算法也用于克服PF算法中存在的粒子贫化不足的问题[61,62]。

(4) H无穷滤波器(HIF)。Elsayed和Grimble在1989年首次引入HIF[63]，基本思想是使滤波误差系统传递函数的H无穷范数最小，以保证噪声或系统误差对SoC估计误差的范数小于给定的衰减水平。文献[64]提出了一种基于HIF的SoC估计方法，与传统的KF方法相比，该方法在不要求系统的精确性和测量误差的前提下仍能保证SoC估计精度，对外界信号和动态模型中的不确定性也不敏感。在对EIS进行分析的基础上，文献[65]基于一种EIM模型，设计了一个HIF用于电池SoC的估计，提高了电池电压的估计精度。

(5) 其他状态观测器。文献[66]通过简单的比例积分整定过程，将比例积分控制器作为观测器的有效解，开发了一种参数实时调整的变参数电路模型。文献[67]利用偏差补偿递推最小二乘法实现在线参数辨识，并结合LO进一步实时估计SoC。文献[68]采用分数阶模型结合SMO实现了SoC的高精度估计，但由于分数阶非线性的特点，离线数据只能用来建立该模型，因此在工程上的应用受到了明显的限制。文献[69]考虑了锂离子电池在实际应用中温度的变化以及电池老化引起的容量变化，采用递归拟合技术自动更新电池的可变参数，并提出了一种改进的基于时变模型的离散滑模观测器以建立SoC估计器。

3.4 基于数据的估算方法

基于数据的估算方法是指通过测量电池参数如电流、电压、温度、内阻等，利用电池数据对SoC进行直接估计。近年来随着机器学习领域的快速发展，数据驱动的SoC估算方法常使用机器学习平台，通过智能算法自动学习网络参数并从中获取电池参数和SoC之间的关系[70,71]。常用于SoC估计的机器学习方法有神经网络与深度学习[72]、支持向量机(Support Vector Machine, SVM)[73]与极限学习机(Extreme Learning Machine, ELM)[74]等。基于数据的估算方法如图4所示。

图4 基于数据的估算方法

3.4.1 基于神经网络与深度学习的SoC估计方法

人工神经网络也简称为神经网络，是一种利用类脑神经突触联接的结构进行信息处理的数学模型[75]。神经网络的基本结构由输入层、隐含层、输出层组成，用于SoC估计的3层神经网络结构如图5所示。

图5 用于SoC估计的3层神经网络结构

输出层SoC可表示为

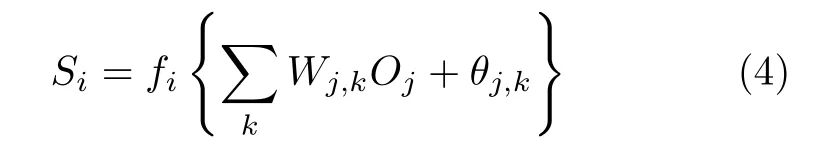
其中，Wj,k和θj,k分别表示隐含层到输出层的权重和偏置，Oj为隐含层的输出，fi为激活函数。

近年来进行SoC估计的神经网络结构主要有小波神经网络(Wavelet Neural Network, WNN)[76,77]、反向传播神经网络(Back-Propagation Neural Network, BPNN)[78]、径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)[79]等。文献[80]将自适应小波神经网络与离散小波变换相结合，提出了一种新的基于小波变换和Levenberg-Marquardt算法的混合小波神经网络模型来估计锂离子电池的SoC。文献[81]提出了一种改进的基于BPNN的锂离子电池SoC估计方法，采用主成分分析和粒子群优化两种算法来提高模型的精度和鲁棒性。文献[82]通过分析电池放电过程中电动势、剩余容量和等效内阻的变化规律，提出一种基于RBFNN的SoC估计方法。

为了解决传统神经网络的一些不足引起的梯度消失、过拟合等问题，基于神经网络的深度学习方法已经引起了学者们的广泛关注。常用于电池SoC估计的深度学习模型有卷积神经网络(Convolutional Neural Network, CNN)和循环神经网络(Recurrent Neural Network, RNN)，其中RNN的发展，尤其是对门控循环单元(Gated Recurrent Unit, GRU)和长短期记忆(Long-Short Term Memory, LSTM)网络的研究，为解决时间序列预测问题提供了新的方向[83]。文献[15]利用了一种LSTM-RNN网络来模拟磷酸铁锂电池的复杂动力学过程，利用电池数据离线训练该网络以建立电池参数与SoC之间的映射关系。文献[84]提出了一种基于GRU的RNN网络来估计锂离子电池的SoC，该方法在初始SoC值不确定的情况下具有很强的鲁棒性，并且能够很好地适应环境温度的变化。

3.4.2 基于SVM的SoC估计方法

支持向量机(SVM)是1995年由Vapnik等人基于统计学学习理论的结构风险最小化原则提出的，主要功能是将具有非线性特征的样本数据映射，并通过其核函数将输入的样本数据映射成高维特征向量，从而形成了输入数据与输出结果之间的非线性关系[85,86]。

为了提高模型的泛化能力和训练速度，文献[87]同时采用粒子群优化(Particle Swarm Optimization, PSO)算法对SVM参数进行优化，并通过交叉验证对预测模型的性能进行评估，将SoC预测问题转化为非线性回归问题。文献[88]建立了基于小样本集的最小二乘支持向量机(Least Squares Support Vector Machine, LS-SVM)模型进行SoC估计，有效减少了计算时间。

3.4.3 基于ELM的SoC估计方法

极限学习机(ELM)是一种针对单隐含层前馈神经网络的新算法，随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，与传统的BP神经网络算法相比，ELM具有良好的学习能力、较高的学习精度和较快的响应速度[89]。文献[90]用ELM法估算锂离子电池的SoC，然而隐藏的神经元是随机测定的，很难获得好的估计结果。为了提高ELM算法的计算性能，文献[70]采用引力搜索算法搜索隐含层神经元最优值，提出了一种改进的ELM方法建立锂离子电池SoC估计模型，通过在不同的操作条件下确定相应的隐层神经元的适当值，加快计算速度。

3.5 混合方法用于SoC估计

将两种或多种方法结合应用，形成一种混合方法，可以利用不同算法的优点来有效提高SoC的估计性能。近年来，学者们常利用数据驱动方法的优化方法结合基于模型的算法来提高SoC估计的准确性、鲁棒性和估算速度。

为了提高电池模型参数的动态跟踪精度，文献[91]将部分自适应遗忘因子递推最小二乘算法应用到ECM中，根据模型各参数本身的物理特性来调整遗忘因子，以适应在深放电范围和高动态工作条件下的变化。文献[92]采用偏最小二乘回归和移动窗口法建立了可以自动更新参数的分段线性电池模型，并结合线性卡尔曼滤波器来估计电池SoC，这种混合方法参数自动更新，不需要额外的参数识别方法，使线性卡尔曼滤波器的应用成为可能。文献[93]结合离散状态空间模型和自适应神经补偿器的方法来预测电池的SoC，它综合了组合状态空间模型的有效性以及神经补偿器的运行鲁棒性和自学习功能。文献[94]采用鲁棒递归最小二乘法对ECM的参数进行在线提取，并结合HIF实现了SoC估计，该混合方法将模型参数估计误差作为未知噪声添加到辨识模型中，能够抑制未知模型误差引起的干扰。

此外，自适应神经模糊推理系统是神经网络学习方法与模糊推理系统相结合的一种改进算法，该算法在映射、建模、决策、信号处理和优化等方面具有强大的功能，近年来也被用于电池SoC估计中[95–97]。

4 SoC估算方法对比分析

锂离子电池SoC估算方法可以分为5类：查表法、安时积分法、基于模型的估算方法、基于数据的估算方法以及混合方法。表2列出了各类算法的优缺点。

表2 各类SoC估计方法的主要优点和缺点

查表法是一种离线SoC估算方法，通过查找表可以准确快速地获得SoC值，不需要对电池建模和计算，但是利用查表法估算SoC的精度依赖于查表的准确度，并且电池的开路电压或内阻需要较长时间的静置才能达到稳定状态。

安时积分法只需要测量系统中流入流出的电量来对电池SoC进行估算，估算速度快且易于实现，是在实际工程应用中使用最多的一种SoC估计方法。然而安时积分法是一种开环估计方法，非常依赖于初始值的准确性和传感器测量值的准确性，经过长时间的电流积分，会存在累计误差。

基于模型的估算方法是一种闭环估计方法，不需要对初始SoC有精确了解，能够通过非线性估计算法计算误差增益。在实际应用方面，基于模型的SoC估算方法的主要缺点是建立模型的过程耗时长且复杂度高，并且参数在线辨识难度大。另外，锂离子电池是一个高度复杂的非线性时变系统，所建立的电池模型很难准确模拟不同放电条件下的电池状态，估算精度依赖于模型精度和参数辨识的准确程度。基于模型的估计的特点启发我们在保证估计精度的同时，简化电池建模过程和降低整个估计结构的复杂性。

基于数据的估算方法具有较强的学习能力，学习精度随着历史学习信息的积累而逐渐提高。与基于模型的SoC估算方法相比，基于数据的SoC估算方法不需要有关电池内部化学、复杂反应和模型参数估计的信息，只需利用历史监测数据寻找并发现规律，进而判别系统的荷电状态，省去建立物理模型的烦琐过程。然而，该方法对数据的高度依赖意味着数据的质量在很大程度上决定了模型的准确性和性能，例如数据量小或错误数值多常导致模型过拟合和欠拟合。

混合方法将基于模型的非线性观测算法与基于数据驱动的方法相结合，综合各自的优点，提高了SoC估计的准确性和鲁棒性。在大多数情况下，优化方法与基于模型和数据驱动的方法一起使用，这不仅提高了性能，而且提供了准确的估算结果。混合方法综合了多种算法和模型，会增大计算复杂度，使系统的能耗增大且估算速度变慢，在实际工程应用中不易实现。

在SoC估算领域，对基于模型和数据驱动的方法已经进行了大量的研究并取得了显著的效果，基于模型的SoC的估计方法适用于先验的系统模型，而在系统模型未知的情况下，使用基于数据驱动的估计方法能够获得更好的效果。近年来，由于处理器的发展，数据处理能力的提升，越来越多的研究指向数据驱动和基于模型方法相结合的估算方法。

5 结论与展望

SoC估算对于锂离子电池在电动汽车中的应用至关重要，本文首先介绍了锂离子电池的特性以及SoC估算中遇到的困难，对近年来用于锂离子电池SoC估算的相关方法进行了较为系统的综述，根据其性质将基于锂离子电池的SoC估算方法分为5类，并分别讨论了各自的优点和局限性。

近年来，对电动汽车锂离子电池SoC估计的问题已经引起较多学者的关注，有越来越多的估算算法应用到对电池SoC精确估计的问题上，然而未来尚有一些可以改进的方向：

(1) 将电池内阻、电池老化状态等参数加入到对电池SoC估计中，以提高算法的估计精度。

(2) 现有工作多是在实验室中进行仿真实验，在不同自然环境下(如雨、雪、冷、热、潮湿等天气)的算法估计性能有待研究。

(3) 从实际应用角度出发，估算成本问题以及算法在实际应用中的可实现性有待进一步考虑与研究。

(4) 目前的算法多是针对单体电池进行估算，然而实际中锂离子电池多以电池组的形式应用，对电池组SoC估算方法的研究尚未展开。

因此，在今后的研究方向上，可以重点关注锂离子电池SoC估计算法的实际应用性和成本问题。