航空发动机滚动轴承故障特征频率研究

王景霖，曹 亮，沈 勇，张 青，付 宇

（1.故障诊断与健康管理技术航空科技重点实验室，上海201601；2.中国民航大学 航空工程学院，天津300300）

滚动轴承是航空发动机转子系统中的主要部件，其工作状态直接影响到航空发动机是否安全、经济、可靠的运行。与其它部件比较，航空发动机滚动轴承寿命的差异相对较大，相同的设备，相同的制造材料，相同的工人，同一制造工艺制造一批轴承，其寿命可能会有很大的不同。有的轴承可能会在设计寿命内发生故障而失效。一旦滚动轴承发生故障而没有及时被维修工作人员发现，转子会出现不平衡的情况，高速旋转的叶片会瞬间撞击机匣，这样的撞击可能还会导致设备损坏，造成严重的经济损失，严重的可能还会伴随着人员伤亡，因此对发动机滚动轴承而言，需要采取及时地状态监控和故障诊断。

目前的航空发动机采用机载振动监控系统（airborne vibration monitoring system，AVM）来监测发动机零部件的振动情况，并收集记录振动信号。但是，由机载振动系统（AVM）测量的振动信号不仅包括轴承的振动响应，还可以包括齿轮的啮合振动或齿轮箱的振动响应信号。就滚动轴承的故障诊断而言，如何将这些信号分离就显得很重要[1-2]。因此，文中使用实验测量的故障数据作为源信号，应用Fast-ICA（快速独立分量分析）算法程序，将轴承振动信号中的故障信号分离出来，然后将包络谱分析得出的结果与公式计算出的理论轴承故障特征频率相比较，确定轴承的工作状况。这样的故障诊断，可以有效地防止设备因为滚动轴承早期故障而突然失效，防止重大安全事故和经济损失的发生。

1 信号分析

独立分量分析是一种高效率的数据信号处理方法，它能够从含有源信号的混合信号中提取或者分离出目标源信号。独立分量分析是伴随着盲源分离（BBS）的出现并且迅速发展的，盲源分离（BBS）是一个很历史的研究课题，“鸡尾酒会”问题就是一个非常典型的盲源分离案例[3]。假想一个情景，某一个鸡尾酒会，大厅里面有一组放在不同位置记录声音的麦克风，麦克风可以记录参与人员说话的声音、音乐的声音以及其他一切声音，因此它记录的是周围环境所有声音的信号混合物，也就是盲源分离中的观测信号。所以问题就是从观测信号的信号混合物中分离出每个人的话语声音，也就是源信号。假设该混合的系统是已经知道的，那么问题就转化为求逆操作混合矩阵，在现实中，这个混合系统对于人们来说是未知的，因此就要根据观测信号推理出源信号，这也就是盲源分离。文中经过独立分量分析提取出目标源信号，之后再采用包络谱分析分离出的轴承故障振动信号，与故障特征频率理论值比较，确定轴承是否发生故障。

1.1 快速ICA 算法

本文应用的算法程序是基于负熵的Fast-ICA算法[4-5]，负熵可以当作是非高斯性的度量，这之前已经被概率论证明了，所以混合信号的分离最大化了信号的非高斯性质。现在假定存在一个变量是y的随机向量，该随机的向量y 的熵如下式所示：

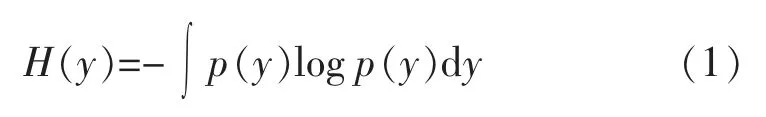
负熵是新定义的一种关于熵的形式，它都是正值或者为零，负熵J：

从上式能够知道，如果这个随机变量服从高斯分布，那么它的负熵为0。Hyvarinen 利用最大熵定理来表示负熵的近似值[6]，公式是：

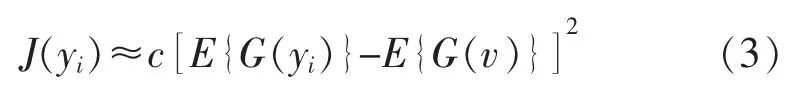
式中：c 为常数；v 为一个标准化高斯变量；G 不是一个二次函数，变量是一个之前已经被标准化的随机变量。ICA 算法最大化后：

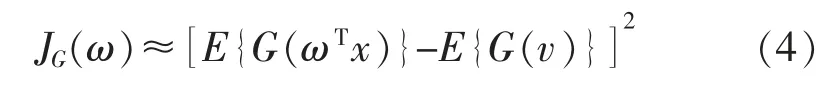
得到一个独立分量：yi=ωTx。ω 满足以下限制条件：

快速ICA 算法主要步骤如下：

（1）对观测数据X 白化处理，均值等于零；

（2）选择分量的数目m，设迭代次数p←1；

（3）选择一个随机初始权向量W；

（6）如果Wp不收敛的话，返回第5 步；

（7）令p=p+1，如果p≤m，返回第4 步。

1.2 包络谱分析

在独立分量分析分离出轴承故障振动信号之后，把分离出的故障振动信号进行包络解调分析，通过与计算出的理论故障特征倍频进行比较，确定故障的类型和位置。这样可以有效地避免滚动轴承因为早期失效而导致发动机故障，对航空器安全和经济的营运有着重要意义。包络谱分析[7-9]是对信号Hilbert 变换，然后再作FFT 变换。

对于一个给定的时域信号x（t），它的Hilbert 变换是：

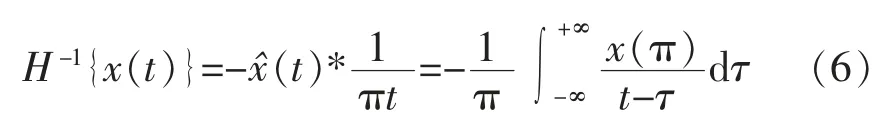
x（t）的解析信号就可以被定义为

对x（t）的解析信号作快速傅里叶变换（FFT），就可以获取信号的幅值调制信号：

该信号的包络就是解析信号图上的幅值。

2 航空发动机滚动轴承故障实例分析

2.1 实验数据和滚动轴承相关数据

本文研究的轴承内圈故障数据来自某大学，其在官方网站上面公布了采集的轴承故障振动信号数据，以mat 数据的形式。滚动轴承故障测试仪器如图1 所示。

图1 测试仪器图Fig.1 Test equipment figure

试验台包括测力器（右）、扭矩传感器（中间）、电动马达（右）、电子控制装备（没有显示）。测试轴承有不同故障规格的单点故障，通过电火花加工而得。测试轴承是深沟球轴承，型号分别是风扇端（SKF6203）和驱动端（SKF6205）。

电机的壳体风扇端与驱动端的12 点位置放置了一个加速度计，它可以连接到电机的支撑板上面或者电机的壳体上，其用来收集振动信号，以每秒12000 个采样点速度采集并记录。轴承故障如图2所示。

图2 滚动内圈故障图Fig.2 Inner ring fault figure

表1 轴承的故障尺寸Tab.1 Bearing fault size

表2 风扇端轴承几何尺寸Tab.2 Fan bearing geometry size

表3 驱动端轴承几何尺寸Tab.3 Driving part bearing geometry size

以上3 个表格描述了轴承故障尺寸和风扇端（和驱动端）轴承几何形状。在本次试验中，1797 r/min是驱动端转速，并且驱动端的滚动体个数是9 个，风扇端转速是1750 r/min，风扇端有8 个滚动体。跟据上面的数据，能够计算出滚动轴承内圈在不同转速下的理论故障特征频率。因此，当转速是1797 r/min时的条件下，驱动端内圈理论故障特征频率是：

风扇端轴承内圈理论故障特征频率：

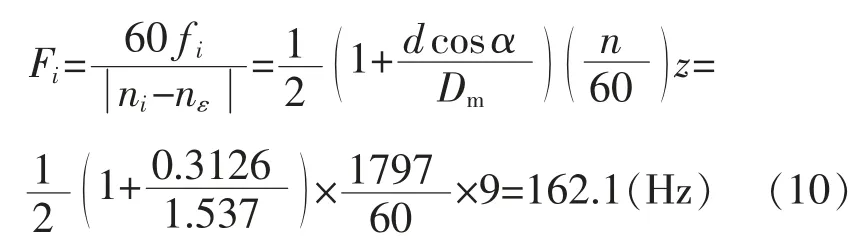
2.2 滚动轴承内圈故障分析

仿真用的是来自凯斯西储大学实验中的轴承故障振动数据和正常振动数据，但是在现实情况下可能会有一些其他信号的干扰，所以假设有s1和s2两路干扰信号，s1是公式中的f1=20 Hz，s2是一个随机噪声信号，其表达式是：

2.2.1 风扇端（SKF6203）

从实验中选取轴承风扇端的故障振动信号数据，并把它和算法程序一起在MATLAB 软件中打开、运行，将得到一个时域波形图，四路源信号时域波形图如图3 所示。

图3 SKF6203 源信号时域波形图Fig.3 SKF6203 source signal time domain waveform

四路信号混合后的时域波形图如图4 所示。

图4 SKF6203 混合后的时域波形图Fig.4 SKF6203 mixes time domain waveform

将混合信号经ICA 分离后的时域波形图如图5所示。

图5 SKF6203 ICA 分离信号图Fig.5 SKF6203 ICA separation signals

将提取出来的第二路轴承故障振动信号作包络谱分析，得到图6，从图中可以明显看出滚动轴承内圈的故障特征频率是144.8 Hz，与公式计算出的理论轴承故障特征频率144.3 Hz 相差较小，误差为0.35%。

图6 SKF6203 包络谱分析图Fig.6 SKF6203 envelope spectrum analysis diagram

2.2.2 驱动端（SKF6205）

从实验中选取轴承驱动端的故障振动信号数据，把它和算法程序一起在MATLAB 软件中打开并运行，将得到一个时域波形图。内圈故障时域波形源信号图包含四路信号，第一路是轴承正常工作信号，第二路是轴承故障的信号，第三路是加入干扰的正弦信号，第四路是随机噪音干扰信号，如图7所示。

图7 SKF6205 内圈故障源信号时域波形图Fig.7 SKF6205 inner ring fault signals

通过一个随机混合矩阵A 将上面四路信号（故障信号，正常信号，干扰信号噪音信号）混合在一起，其混合后的时域信号波形图如图8 所示。然后应用Fast-ICA 算法程序处理混合信号，ICA 分离信号后的时域波形图如图9。

图8 SKF6205 内圈故障混合信号时域图Fig.8 SKF6205 inner ring fault mixed signals

图9 轴承故障ICA 分离信号图Fig.9 Bearing fault ICA separation signals

采用包络谱分析经过ICA 分离出的轴承故障振动信号，分析结果如图10。

从图10 可以得出包络谱分析结果为161.8 Hz，与上文公式计算出的理论轴承特征频率很接近，只有很小的误差，大约在0.19%。

图10 SKF6205 轴承故障信号包络谱分析图Fig.10 SKF6205 bearing fault signal envelope spectrum

综合以上两次滚动轴承内圈故障分析，在不同转速、不同规格型号的情况下，Fast-ICA 都可以稳定的分离出轴承内圈故障振动信号，再通过包络谱解调分析，该信号的包络就是解析信号图上的幅值，可以稳定的提取出其故障特征频率。

2.3 数据分析

Fr是内圈故障的特征频率理论计算值，Fa是经过Fast-ICA 算法分离后的信号的包络谱分析结果。滚动轴承试验采样参数如表4 所示，Fast-ICA 算法的误差率如表5、表6 所示。

表4 数据采样参数Tab.4 Sampling parameters

表5 SKF6203 的Fast-ICA 算法误差率Tab.5 SKF6203 Fast-ICA algorithm error

表6 SKF6205 的Fast-ICA 算法误差率Tab.6 SKF6205 Fast-ICA algorithm error

通过上面两个表格的数据可以看出，对滚动轴承内圈而言，快速不动点算法（Fast-ICA）可以很好地把轴承故障振动信号分离出来，并且误差率都小于1%。

3 结语

本文基于航空发动机滚动轴承的故障诊断研究，提出了独立分量分析，利用凯斯西储大学的试验数据，对轴承的故障振动信号进行分离（记录的振动信号不仅包括轴承的振动信号，另有可能也包括齿轮相互啮合产生的振动信号和齿轮箱振动响应信号或其他周围环境噪音信号）。本文使用了一种基于负熵的快速固定点算法（Fast-ICA）来分离故障信号，并对分离后的故障信号进行包络谱分析（其幅值就是它的包络），然后和公式计算出的理论轴承内圈故障特征频率作对比，验证了快速不动点算法 （Fast-ICA） 对轴承内圈故障信号分离的有效性。以轴承内圈数据为例，分析了两组滚动轴承内圈故障（风扇端（SKF6203）和驱动端（SKF6205）），在不同转速、不同规格型号的情况下，Fast-ICA 都可以稳定的分离出轴承内圈故障振动信号，再通过包络谱解调分析，该信号的包络就是解析信号图上的幅值，可以稳定的提取出其故障特征频率。计算与数据分析表明，SKF6203 轴承在转速1750 r·min-1时，其内圈故障的特征频率理论计算值为144.3 Hz，包络谱分析后故障振动信号特征频率为144.8 Hz，误差率0.35%；SKF6205 轴承在转速1797 r·min-1时，其内圈故障的特征频率理论计算值为162.1 Hz，包络谱分析后故障振动信号特征频率为161.8 Hz，误差率0.19%；均取得了良好的效果，这种分析方法能够正确的检测出滚动轴承故障。