居民小区电动汽车有序充电策略研究

李海斌，李正明，汪 洋

（江苏大学 电气信息工程学院，镇江212013）

随着全球能源日渐枯竭，环境问题日趋严峻，电动汽车因其零排放、零污染的特点得到迅猛发展。工信部电动汽车发展战略研究报告预测[1]，到2030年，我国电动汽车保有量有望达到7000 万辆[1]。如此庞大数量的电动汽车若任由车主进行无序充电，尤其是在用电高峰期，势必会对电力系统的安全稳定运行产生负面影响[2]。因此，亟需制定相应的充电调度策略。

针对电动汽车有序充电问题，许多专家、学者已做出大量研究。文献[3]建立以购电成本最低为目标的充电站需求响应模型，并用滚动线性规划法求解。文献[4]基于分布式控制思想，用拉格朗日松弛法决策各电动汽车的充电计划，旨在获得最大收益。以上两个研究的优化算法尽管收敛速度较快，但难以应对多维度、多极值的复杂充电模型。文献[5]基于分时电价构建充电费用最低和开始充电时间最早的优化模型，对电网产生了削峰填谷作用，但仅考虑了电动汽车用户的利益，且易在谷时电价起始处产生新的用电高峰。文献[6]研究了换电站的换电池问题，将电池数量视作控制变量，建立了负荷波动最小的优化调度模型，提出一种改进的布谷鸟算法并求解。文献[7]建立了充电功率分布的两阶段优化模型，并借助多种群遗传算法求解，实现对电动汽车充电时间和功率的双重优化。文献[8]着眼于提高居民小区充电站的收益，提出网格选取法，简化求解且优化效果好。以上研究均采取可间断充电方式，尽管能提升车辆的充电灵活性，但频繁的通断电会缩短电池的使用寿命，一定程度降低了用户参与调度的积极性。

鉴于此，本文以某居民小区的电动私家车为研究对象，基于峰谷分时电价和不间断充电方式，以配电网用电负荷波动最小和电动汽车充电费用最低为目标，建立有序充电优化模型，并采用布谷鸟算法求解出各车的最佳开始充电时间，进而完成对车辆的优化调度。最后，依据算例仿真，验证本文所提策略的优化效果。

1 分时电价与电动汽车充电负荷

1.1 峰谷分时电价

峰谷分时电价是电力部门依据用电负荷波动情况，划分一天为峰、平、谷3 种时段类型，并分别制定电能价格。是当前供电公司积极推广的一种电价制度。用户通过响应峰谷分时电价，选择在电费较低廉的谷时段或者平时段用电，可降低日常电费支出；通过转移电网的高峰用电至低谷时段，高峰电力的供需缺口得以缓解，促进电力资源的优化配置[9]，实现对电网的削峰填谷。本文采用文献[10]中北京市电力公司制定的公共充电桩电价，具体电价信息如表1 所示。

表1 分时电价数据Tab.1 Data of time-of-use electricity price

1.2 居民出行特性

居民出行特性，包括早晨离家、晚上归家时间，车辆荷电状态（state of charge，SOC）等。充电所需时长可由SOC、充电桩的充电功率、效率计算得出。

根据美国交通部对全美私家车的调查统计[11]，车辆的最后返回时间Tr服从正态分布，概率密度函数如式（1）所示：

式中：μr为期望值，取17.47；σr为标准差，取3.41。

同样，车辆的最早离家时间Td服从正态分布，概率密度函数如式（2）所示：

式中：μd为期望值，取8.92；σd为标准差，取3.24。

归家时车辆的初始电量SOCr满足正态分布N（0.6，0.12）[12]。

电动汽车充电所需时长的计算公式如式（3）所示：

式中：Tc为充电所需时长；SOCd为车主离家时的期望电量；Bm为电池容量；Pc，ηc分别为充电桩的充电功率和效率。

1.3 基于蒙特卡洛的电动汽车充电负荷计算

蒙特卡洛法是一种利用随机数数列进行模拟试验[13]的数值计算方法，为服从某概率分布的变量随机抽取大量数据，进而实现模拟预测。

单个车辆的充电行为具有较强的独立性和随机性，难以预测且研究意义不大。大数据下，居民的出行数据可经分析、归纳近似满足相应的概率分布，如式（1）、式（2）所示。借助蒙特卡洛法抽取车主归家、离家时间及车辆的初始剩余电量等数据，得到各车对应的充电时段，叠加计算出车辆的总充电负荷。再以负荷的方差系数评判蒙特卡洛模拟的精度[12]，直至满足精度要求完成收敛，实现对小区电动汽车充电行为的模拟。图1 为电动汽车充电负荷计算的流程。

图1 充电负荷计算流程Fig.1 Charging load calculation flow chart

2 电动汽车有序充电控制

2.1 电动汽车有序充电优化模型

为兼顾配电网和用户的利益，有序充电既要求保障电网安全稳定运行，又强调降低电动汽车用户的充电费用。本文建立了多目标优化模型。

2.1.1 目标函数

目标函数1配电网负荷波动最小

负荷波动对应配电网运行的安全稳定性。负荷波动越小，负荷曲线越平滑，网络损耗越低。此目标函数可表示为

式中：M 为将一天平均划分的小时间段数，本文取96；N 为电动汽车数量；Si，j为第i 辆车j 时段的充电状态，当Si，j=0，表示未充电；当Si，j=1，表示正在充电；L0，j为j 时段居民小区的基础用电负荷；Lav为当日小区总用电负荷的均值。

目标函数2电动汽车充电费用最低

基于峰谷分时电价，在满足车主出行需求的前提下，转移电动汽车的充电负荷至电网负荷较低的（谷、平）时段，削减电费。该目标函数可表示为

式中：Pj为j 时段的电价；Δt 为单个小时间段的长度，本文取15 min。

2.1.2 约束条件

1）充电时间约束

基于不间断充电的方式，电动汽车只能在小区的停留时间段内连续充电，即归家后方可开始充电，离家前必须结束充电。

式中：Ts，i，Tr，i分别为 第i 辆车的开 始充 电 和归家时间；Te，i，Td，i分别为第i 辆车的结束充电和离家时间；Tc，i为第i 辆车的充电时长。

2）电池电量约束

电动汽车结束充电时，其电量应当不低于用户的期望值，且不超过电池总容量。

式中：SOCd，i，SOCr，i分别为第i 辆车的用户期望电量和初始剩余电量。

那也是香港电影的黄金时代。夏天的太阳晃得刺眼，暑假属于盗版VCD、周星驰的喜剧片、花里胡哨的鬼片、还有古惑仔系列，把青春期的小孩看得心潮澎湃。前段时间，《古惑仔》原班人马拍的《黄金兄弟》上映了，浩南、山鸡都已青春不再，岁月对男艺人也是一样的心狠手辣。

3）变压器容量约束

为保证配电网的安全稳定运行，小区总用电负荷必须低于变压器的最大可用有功功率。

式中：STN，λT，ηT分别为变压器的额定容量、功率因数和效率。

2.2 基于布谷鸟算法的优化求解

布谷鸟搜索算法（cuckoo search algorithm，CSA）是英国剑桥大学教授Yang[14]提出的一种新型启发式算法，该算法模仿了布谷鸟巢穴寄生繁殖和Levy飞行搜索[6]的行为，具备较强的搜索能力和通用性。

2.2.1 布谷鸟巢穴寄生

布谷鸟在其他鸟类的巢穴中产卵，并选择合适时机以提高孵化率。此外，有研究表明，刚孵化的小布谷鸟会本能地模仿宿主鸟幼雏的叫声以及破坏巢中的其他卵[15]。但是，宿主鸟依然有一定概率Pa发现部分不善伪装的布谷鸟卵，继而丢弃现有巢穴选择去别处重新筑巢。而新巢位置的选择具有一定规律，可充分利用鸟巢间的相似性，采用偏好随机游动加以确定。具体公式可表示为

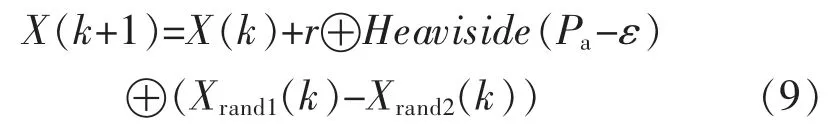
式中：X（k+1）和X（k）分别为第（k+1）次和k 次迭代时鸟巢的位置；r 和ε 均为0～1 的随机数；Heaviside（x）为阶跃函数，当x≥0 时，函数值为1，否则为0；Xrand1（k）和Xrand2（k）为第k 次迭代时随机抽取的某两个鸟巢位置。

2.2.2 Levy 飞行

Levy 飞行是一种随机游走机制[16]，步长由高频次的短步长和低频次的长步长共同组成，既保证了搜索精度又能避免陷入局部最优。在CSA 中，布谷鸟定期寻找新的宿主鸟巢产卵以提高整体孵化率，而Levy 飞行能形象地描述布谷鸟的飞行路径，即较准确地表示新鸟巢位置的更新。Levy 飞行的公式可表示为

其中：

式中：Xi（k+1）和Xi（k）分别为第（k+1）次和k 次迭代时第i 个鸟巢的位置；α 为步长缩放因子；Levy（β）为Levy 飞行的随机步长；u，v 是满足相应正态分布的随机数；Xbest（k）为第k 次迭代时适应度值最好的鸟巢位置；β 为常数，通常取3/2。

图2 为布谷鸟算法的运行流程。

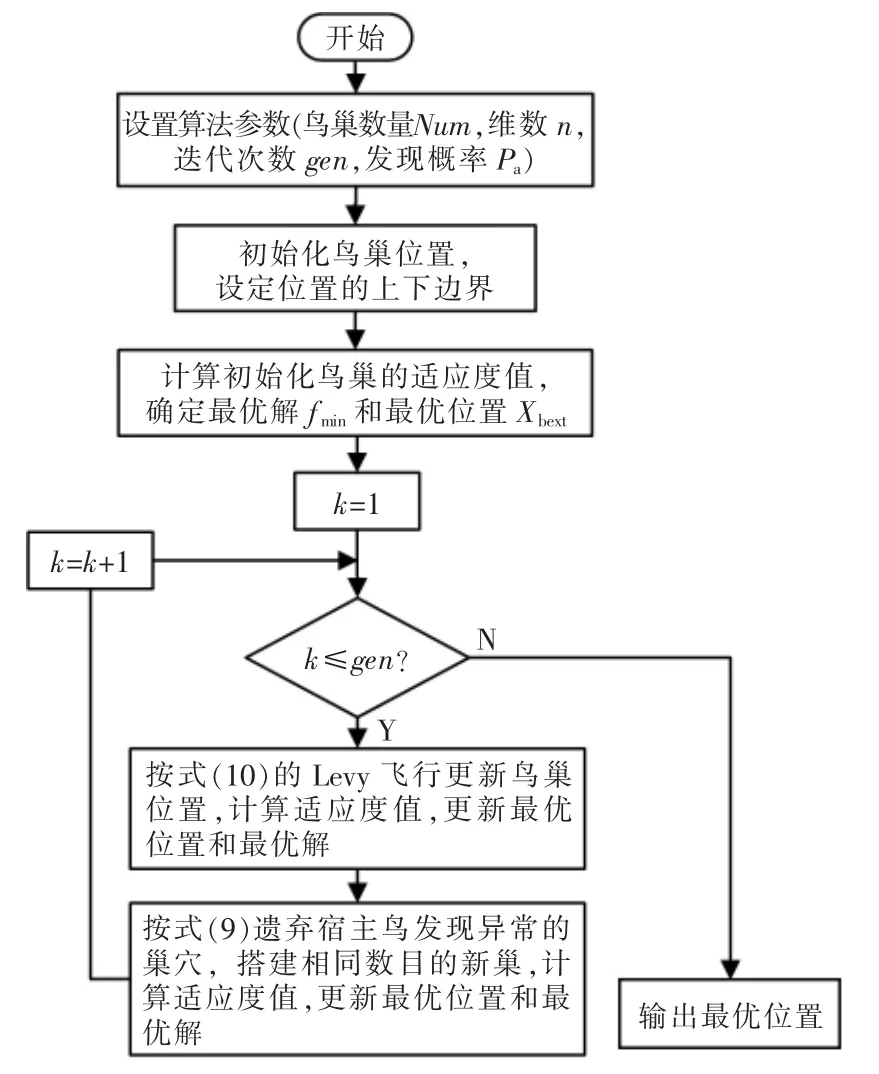
图2 布谷鸟算法流程Fig.2 Flow chart of CSA

在基于CSA 优化求解电动汽车有序充电的问题中，鸟巢维数对应电动汽车数量n，鸟巢位置表示各车的开始充电时间。根据前文中车辆的归家、离家时间设定上下边界，初始化生成一组符合要求的数据，经布谷鸟算法多次迭代更新，保留适应度值最优的鸟巢位置即为一组最优的开始充电时间。

3 算例分析

3.1 仿真参数设置

仿真算例中的居民小区有650 户业主，平均每2户拥有1 辆汽车。配电变压器额定容量为1600 kVA，功率因数、效率分别为0.85 和0.9，即最大可用有功为1224 kW。记录小区某个典型日的基础用电负荷[8]，绘制曲线如图3 所示。具体的分时电价参见表1。车主的最晚归家和最早离家时间分别按式（1）和式（2）进行抽取模拟。车辆的初始剩余电量满足正态分布N（0.6，0.12）[12]，期望电量取0.95。电动汽车型号统一为“帝豪EV450”，其电池容量52 kWh，充电功率、效率分别为7 kW 和0.9。

图3 居民基础用电负荷曲线Fig.3 Basic load curve of residents

算法中，鸟巢数量Num 和最大迭代次数gen 设置为100，发现概率Pa取0.6。

3.2 仿真结果分析

按3.1 节设置好仿真参数，分别假设小区电动汽车的渗透率为20%和40%，讨论不同数量电动汽车参与无序和有序充电时的负荷情况。

当渗透率为20%，即电动汽车保有量为65 辆时，其充电负荷曲线如图4 所示。

图4 20%渗透率下电动汽车的充电负荷Fig.4 Charging load of electric vehicles with 20%penetration rate

由图4 可知，电动汽车的充电负荷发生了偏移。其中，负荷高峰段由20 点附近向后偏移到22 点至次日凌晨4 点间； 负荷低谷段由8 点至11 点向后偏移4 h。通过转移部分高峰充电负荷至电价较低的谷、平时段，总电费由2032.81 元降至1586.43元，平均每位车主可节省约6.8 元的支出。

此时，将充电负荷和居民基础用电叠加，可得如图5 所示的居民小区总用电负荷曲线。

图5 20%渗透率下的总负荷Fig.5 Total load with 20% penetration rate

由图5 可知，居民小区的总负荷得到了“削峰填谷”。其中，负荷最高值由1159 kW 降至1035 kW，降幅达10.69%；负荷最低值由535 kW 升至694 kW，涨幅达29.72%。

当渗透率为40%，即电动汽车保有量为130 辆时，其充电负荷曲线如图6 所示。

图6 40%渗透率下电动汽车的充电负荷Fig.6 Charging load of electric vehicles with 40%penetration rate

由图6 可知，电动汽车充电负荷的分布情况与图4 相类似。经分析计算得知，总电费由3877.01 元下降为3135.93 元，即平均每位车主可节省约5.7元的支出。

图7 为电动汽车40%渗透率下居民小区的总用电负荷曲线。

图7 40%渗透率下的总负荷Fig.7 Total load with 40% penetration rate

由图7 可知，此时居民小区的负荷最高值由1432 kW 降到1217 kW，降幅达15.01%；负荷最低值由547 kW 升到737 kW，涨幅达34.73%。

综上所述，本文所提充电策略在降低电动汽车充电费用和平滑配电网用电负荷曲线等方面均具有较好的优化效果。表2 为两种渗透率下，电动汽车参与无序和有序充电的详细统计数据。

表2 充电统计数据对比Tab.2 Comparison of charging statistics

4 结语

文中提出了一种基于CSA 的电动汽车有序充电策略，该策略设定对车辆进行不间断充电，既能避免汽车频繁的通断电，又可以简化充电调度问题的研究。同时借助布谷鸟算法寻优求解得到最优的开始充电时间，确定充电时段，制定出符合用户和配电网双方利益的充电安排。由算例仿真的结果可知，该策略能够减少车辆的充电费用，降低车主的实际用车成本； 同时平滑总负荷曲线，降低配电网用电负荷波动，实现削峰填谷。