基于双滑模的PMSM传感器故障诊断与容错控制方法

王 玥

（西安工业大学 电子信息工程学院，西安710021）

永磁同步电机（简称PMSM），因为其轻量级，可达到理想的功率密度，且具有良好的抗过载能力，所以在各行各业中具有较为广泛的应用，并得到了迅速发展[1]。过去所一直沿用的PMSM 控制系统当中，会发生PI 控制器稳定性不佳的问题，PI 控制器容易受外界扰动影响，降低系统调速性能[2]。除此之外，由于必然存在负载变化和环境影响，速度传感器极易发生故障，使系统本身的控制性能不佳，不利于系统的长期运行[3]。故而，对其速度传感器可能发生的故障，进行严谨的诊断十分必要，同时还需要研究出有效的容错控制方法。

目前，PMSM 的故障诊断与容错控制系统多采用基于模型的方法，利用系统模型设计观测器，将观测状态量与测量状态量之间的残差作为故障判断依据。一般情况下，观测器可细致划分为若干类别，其中包含Luenberger 观测器[4-5]、滑模观测器等[6-7]。文献[4]秉持极点配置思想，借助变增益Luenberger观测器的作用，围绕PMSM 系统研究得到相对完善的控制方法，此设计方法能够对转子转速等参数进行较为精准的估算，提高系统的控制性能，但龙伯格观测器适用于噪声污染不严重的情况，不具有普适性；文献[5]以扩展卡尔曼滤波器为基础，研究得到了相应的速度传感器容错驱动系统，保证了系统的鲁棒性。但卡尔曼滤波器状态初始值难以确定，设置不当会导致滤波器发散[8]；文献[9]基于双滑模观测器的作用，研究得到科学合理的故障容错控制法，发生故障后，2 个SMO 分别用于重构电流和估算转子位置及转速，保证了系统在电流传感器故障下的可靠运行，然而，以往所沿用的滑模观测器主要将控制律设定为sign 函数，频繁通断会引发极大的抖振问题。通常情况下，PMSM 系统所选用的速度环主要为PI 控制器[10-11]，其基本结构相对简洁，便于实现，可减小静差，但当系统受到干扰时，无法保障控制过程中的良好鲁棒性。相比之下，滑模控制器不仅在响应速度上极为迅速，而且不会对模型提出严苛的要求，如果据此围绕PMSM 系统展开相应的速度环控制，那么，基于其良好的鲁棒性，可以有效改善系统速度环的鲁棒性和动态响应速度[12]。本文采用双滑模控制思想，基于滑模控制理论的稳定性，提高系统调速性能，与此同时，本文选用sigmod函数，将本来的sign 函数取而代之，提高观测器观测精度。

在本文中，主要围绕PMSM 系统中可能存在的速度传感器故障，以滑模控制器为基础，研究得到相应的容错控制方法等。利用滑模控制器对系统速度环进行改进，提高系统抗干扰能力，将基于滑模观测器所得到的转速和实际转速进行比对，以此获得残差，即能够达到良好的故障检测效果。同时，引入时间分析法进行二次检测，克服外界干扰与固定阈值带来的误检问题。基于所得仿真结果可知，这一方法能对故障进行迅速且精准的检测，同时保持电机系统良好的运行状态。

1 滑模速度控制器设计

在两相旋转坐标系d-q 下，PMSM 系统所对应的机械运动方程为

式中：uq代表q 轴的定子电压；iq代表其电流分量；R代表定子电阻；ψf则代表永磁磁链；与此同时，ωe代表电角速度；ωm代表了转子机械角速度，其中ωe=ωmpn；此外，J 代表转动惯量；TL代表负载转矩。

为了便于分析，定义系统状态变量为

式中：ω*为给定的转速参考值，为常量。结合式（1）有如下形式：

结合式（2）可以得到：

设计滑模面s 为

对滑模控制采用等速趋近律的方法，即

式中：ε1为滑模增益，且ε1＜0。基于此可以得到滑模控制器：

则有：

由式（7）得出q 轴电流参考值为

2 二阶超扭曲滑模观测器设计

两相静止坐标系α-β 条件下，PMSM 系统所表现的定子电流状态，遵循以下方程[13]：

式中：uα，uβ，iα，iβ分别为α，β 的定子电压以及相应的电流分量为扩展反电动势。

设计滑模观测器：

将式（11）与式（10）作差，即能够得到定子电流所对应的观测误差方程为

而设计电流观测误差为

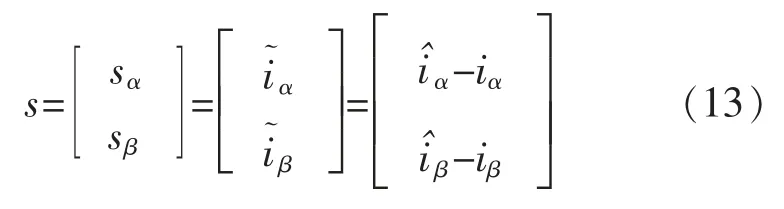
根据等速控制律设计滑模控制规律，并采用sigmoid 函数取代符号函数，即

式中：ε2为滑模增益，ε2＞0；F（·）代表sigmoid 函数；a 为可调参数，其值与滑模趋近速度有关。

如果观测器状态量为s=0，则秉持滑模控制的等效原理，能够得到下述公式：

选取正定Lyapunov 函数为

对式（16）求导可得：

根据观测器估计出的反电动势可以获得转子转速与转子位置[11]：

3 传感器故障诊断与容错控制方法设计

速度传感器因电机工作环境和工作时长的影响，极易发生故障，其频繁发生的故障主要包含恒偏移故障、恒增益故障等，故障模型[14]如下：

恒偏移故障

卡死故障

恒增益故障

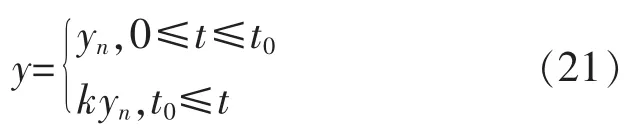
式中：y 为传感器输出值；yn代表传感器的实际输出值；t 为运行时间；t0表示故障发生的时间；c，λ，k 为常数。

根据滑模观测器的观测转速，将其与PMSM 输出转速之间的差值作为故障检测依据。在理想情况下，系统的输出转速与滑模观测器观测转速相等，速度残差为0。如果速度传感器出现故障，同时，速度残差不等于0，则可以将其和预先拟定的阙值进行对比，如果残差已经高于阈值，则能够得到故障之处，该过程公式为

式中：ρ 代表故障情况；en为速度残差；thn为设定的阈值。如果速度残差超过了阈值，那么代表故障已经发生，ρ＝1；如果其小于阈值，则速度传感器正常，ρ＝0。

因为受到参数变化等方面的诸多影响，在系统运行时，输出转速会发生波动，容易造成误检，为了减少这种情况的发生，以时间为基础进行检测。

定义故障检测时间tf，即传感器故障，ρ＝1 持续的时间，其值取决于系统的采样时间ts和灵敏度系数f。

若灵敏度系数过大，可能无法检测到故障；若灵敏度系数过小，则可能造成误检。在设定灵敏度系数时，应多次进行仿真实验，结合系统参数，设置合理数值。

定义时间te为从检测出故障ρ＝1 开始到故障检测时间tf经过的时间。故障检测标志位Flag 定义如下：

如果te＜tf，同时，Flag=0，则表示速度传感器正常；如果te≥tf，那么，Flag=1，即表示速度传感器发生故障。

当已经检测出故障后，需要基于切换控制，将速度环反馈回路与速度传感器切断，选择与观测器相连通，再将反馈量设定为观测器已观测的转速，将其实时传输至系统，即能够达到良好的故障容错控制效果。

上述方法的基本结构示意图如图1 所示。在此速度环中，SMC 将PI 控制器取而代之，利用速度传感器输出转速与SMO 输出观测转速比较产生残差，故障检测后输出故障判断标志位Flag，根据Flag 的值，容错切换控制器选择正常的转速值反馈回系统速度环。

图1 速度传感器故障诊断与容错控制结构框图Fig.1 Structural block diagram of speed sensor fault diagnosis and fault-tolerant control

4 数值仿真与结果分析系

基于MATLAB 软件，可构建出相对应的PMSM系统模型，并以此展开仿真验证，对传感器正常工作情况下传统PI 速度控制器和滑模速度控制器进行仿真对比，与此同时，围绕优化前后的两种滑模观测器，展开科学合理的综合分析，并给予容错控制方面的仿真结果，电机参数如表1 所示。

表1 电机参数Tab.1 Motor parameter

4.1 基于PI 和SMC 的系统仿真对比分析

分别搭建基于PI 控制器和SMC 的PMSM 仿真系统模型。仿真给定转速为Nref=1000 r/min，空载启动并在t=0.2 s 时施加10 N·m 的负载转矩，仿真时间为0.4 s，与此同时，选取滑模增益ε1＝200，a＝1，ε2＝200，α＝60。

速度环分别采用PI 控制器和SMC 时的系统响应波形如图2 所示。其中，图2（a）和图2（b）为分别基于PI 控制器和SMC 的系统三相电流响应波形；图2（c）为基于PI 控制器和SMC 的系统转矩响应波形；图2（d）为基于PI 控制器和SMC 的系统转速响应波形。

图2 基于PI 和SMC 的系统响应波形Fig.2 PI and SMC based system response waveforms

基于图2 所呈现的仿真结果对比能够得知，基于SMC 的系统三相定子电流更快达到稳态，波形更加平滑，转矩到达稳定状态速度更快，转速更快到达给定转速，且超调量小；在负载转矩增大后，基于SMC 的系统响应波形波动小，能更快的到达新平衡状态。验证了滑模控制器较于PI 控制器对速度环有更优越的控制性能。

4.2 基于传统滑模观测器与改进滑模观测器的仿真对比分析

基于传统滑模观测器和基于改进滑模观测器的观测转速与系统输出转速波形，以及二者的观测误差波形如图3 所示。其中，图3（a）和图3（c）为基于传统滑模观测器的转速响应波形及其与系统输出转速之间的误差；图3（b）和图3（d）为基于改进滑模观测器的转速响应波形及其与系统输出转速之间的误差。

图3 基于传统滑模与改进滑模的的响应波形Fig.3 Response waveforms based on conventional and modified sliding modes

基于图3所呈现的仿真对比结果能够得知，基于改进滑模观测器的转速可以更好的跟踪系统输出转速，达到了理想的观测精度，而且不存在较大误差，鲁棒性也极佳。

4.3 速度传感器故障诊断与容错控制

为验证以上方法是否可行，本文基于MATLAB软件，构建出相对应的PMSM 系统模型，并以此展开仿真验证，并给出对速度传感器故障诊断与容错控制的仿真结果。通过试验与经验总结选择故障检测阈值Nth=30 r/min；灵敏度系数f=3；则故障检测时间tf=3 ms。

（1）基于时间分析法的故障检测分析：假设在t=0.2 s 时，由于扰动影响，系统转速发生了一个持续时间为t1=0.002 s 的微小震荡，转速波形出现40 r/min的波动，如图4 所示；时间分析法中检测时间te与故障检测时间tf的变化波型如图5 所示； 引入时间分析法与未引入时间分析法的检测结果对比如图6所示。

图4 转速波形Fig.4 Speed waveform

图4 所示0.2 s 时刻，转速出现持续0.002 s 的波动，转速残差超过阈值。引入时间分析法，计时器开始计时产生时间te如图5 所示，直到转速波动消失，转速残差小于阈值，te清零。

图5 检测时间变化波形Fig.5 Detection of time-varying waveforms

图6（a）表示未引入时间分析法的故障检测结果，转速残差超过阈值，此时代表故障发生，Flag 为1，当波动消失后，转速残差小于阈值，标志置0；图6（b）表示引入时间分析法的故障检测结果，由于te始终小于故障检测时间tf，此时代表不存在故障，Flag 为0。

图6 一般方法与引入时间分析法的故障检测结果Fig.6 Fault detection results of general method and introduction of time analysis

（2）速度传感器恒偏移故障诊断：假设在运行时间t=0.2 s 时速度传感器发生恒偏移故障且偏移240 r/min。速度传感器发生恒偏移故障时的响应波形如图7 所示。

图7 速度传感器发生恒偏移故障的仿真结果Fig.7 Simulation results of a constant offset fault in speed sensor

速度传感器发生恒偏移故障后的系统输出转速和观测器估计转速如图7（a）所示；滑模观测器获得的估计转速与实际转速的残差和阈值如图7（b）所示，在故障发生后，其残差超过阈值。此时，触发故障检测时间te开始计时如图7（c）所示，直到到达故障检测时间Tfault，此时故障检测标志位Flag 置1，如图7（d）所示。

（3）速度传感器卡死故障诊断：假设在运行时间t=0.2 s 时速度传感器发生卡死故障且卡死在940 r/min。速度传感器发生卡死故障时的响应波形如图8 所示。

图8（a）给出了速度传感器发生卡死故障后的的系统输出转速和观测器估计的转速；图8（b）所示为残差和阈值波形，t=0.2 s 出现故障之后，残差高于了阈值；图8（c）所示故障时间te被触发，te计时直到到达故障检测时间Tfault，此时故障检测标志位Flag置1，如图8（d）所示。

图8 速度传感器发生卡死故障的仿真结果Fig.8 Simulation results of a jammed speed sensor failure

（4）速度传感器恒增益故障诊断：假设在运行时间t=0.2 s 时速度传感器发生恒增益故障，故障增益k=0.9。速度传感器发生恒增益故障时的响应波形如图9 所示。

图9（a）为速度传感器发生恒增益故障后的系统输出转速和观测器估计的转速；图9（b）为转速残差和阈值波形，t=0.2 s 出现故障之后，残差高于了阈值；图9（c）为故障时间te被触发开始计时直到到达故障检测时间Tfault=0.003 s，此时故障检测标志位Flag 置1，如图9（d）所示。

图9 速度传感器发生恒增益故障的仿真结果Fig.9 Simulation results of constant gain failure of speed sensor

如果Flag 为1，则检测故障发生，此时基于切换控制，基于观测转速实现闭环控制，切实保障系统的顺利运行。故障容错结果如图10 所示，传感器发生任何一种故障时，都能迅速检测到其故障，并做出相应措施，保证系统的稳定安全运行。

图10 速度传感器故障容错仿真结果Fig.10 Speed sensor fault tolerance simulation results

通过对基于滑模观测器的速度传感器恒偏移、卡死、恒增益故障的诊断与容错控制的仿真，可以看出在快速检测到故障的同时，系统可以将估计转速反馈回系统，很好地隔离了速度传感器的故障，切实保障PMSM 系统的不间断驱动。

5 结语

本文主要围绕PMSM 系统中存在的速度传感器，所发生的恒偏移、恒增益等故障，以双滑模结构为基础，研究得到相应的故障诊断与容错控制方法。速度环采用滑模速度控制器，将其与PI 控制器控制的系统进行仿真对比，证明了滑模速度控制器有助于提升系统自身的调速性能，可达到理想的鲁棒性。在设计滑模观测器后，利用其观测转速与实际转速比较生成残差，结合阈值与故障检测时间进行故障诊断，克服了误检问题。进而根据检测结果，将正常转速实时传递至系统，即能够达到良好的故障容错控制效果。基于仿真结果可知，这一方法能够快速检测出速度传感器故障，并可保障其容错运行，提高了系统的可靠性。