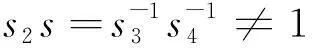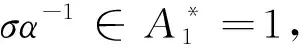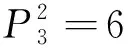有限传递图的偶圈对边集*

2021-07-29 01:41徐尚进

南宁师范大学学报(自然科学版) 2021年2期

徐尚进

(广西大学,广西南宁 530004)

1 引言

图是比较容易被人们直观理解并也容易激发人们产生丰富想像的对象.而图论研究的图,通常是经过抽象以后仅剩下一些顶点和连接这些顶点的边的几何图形.本文所涉及的图则更为特殊,即有限简单无向图,其顶点个数有限且无自环,边不重且无向,并还具有某些对称性.由于图的这些对称性需要通过其全自同构群的某些传递性来描述,因此需要运用群及其作用的理论.这方面工作属于群与图研究领域,我们称之为“传递图”研究.

我们先回顾代数结构的自同构群.

设Ω∶={α1,α2,…,αn}是一个有限集,则Ω到自身的双射(也称为“置换”)的全体关于映射的乘法构成一个n！阶有限群, 称为n次对称群, 记作Sym(Ω).

进一步,若Ω不是一个普通集合,而是一个代数结构,比如Ω是一个偏序集,或者是一个群、一个环,则我们通常会重点考虑Sym(Ω)中保持Ω的代数结构关系的置换σ：

(1) 当Ω是偏序集时,σ要能保持Ω的序,即由αiαj有其中表示αi在σ作用下的象(下同);

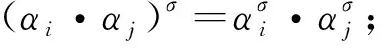
(3) 当Ω是一个环时,σ要能同时保持Ω的加法和乘法, 即

Sym(Ω)中能保持上述代数结构关系的置换称为Ω的自同构.容易验证,Ω的全体自同构组成一个群,称为Ω的自同构群,记作Aut(Ω).显然有

1 ≤Aut(Ω) ≤Sym(Ω).

由于自同构触及Ω的代数结构,因此研究Aut(Ω)及其作用对于了解Ω本身结构是有效的.

有限简单图作为由有限的顶点集和有限的边集决定的组合结构,也同样可以定义它的自同构群,并通过自同构群来研究图本身的性质,特别是图的对称性.为了方便陈述,我们先给出有限简单无向图及其全自同构群等有关概念.

定义1.1有限简单无向图Γ的顶点集记作V(Γ),|V(Γ)|称为Γ的阶.以顶点v,u∈V(Γ)为端点的(无向)边记作{v,u},边集记作E(Γ).与v∈V(Γ)连边的顶点全体称为v的邻域,记作N(v),|N(v)|称为v的度数,记作deg(v).如果Γ的一个由两两不同顶点组成的序列v0,v1,…,vl满足{vi-1,vi}∈E(Γ)(i=1,2,…,l),则这个顶点序列称为Γ的一条l-路,记作[v0,v1,…,vl],其中l称为这条路的长.特别地,长大于2且首尾相等的l-路[v0,v1,…,vl-1,vl=v0]称为l-圈,记作Cl.如果图Γ的任意两顶点之间至少存在一条路相连,则称Γ是连通的.

定义1.2有限简单无向图Γ的一个自同构是指顶点集V(Γ)上保边的一个置换σ∈Sym(V(Γ)),它满足:{u,v}∈E(Γ)当且仅当{u,v}σ∶={uσ,vσ}∈E(Γ).图Γ的自同构全体关于置换的乘法构成Sym(V(Γ))的一个子群,称为图Γ的全自同构群,记作Aut(Γ).

如图1,Aut(Γ1)=1,Aut(Γ2)=Sym({v1,v2,v3,v4})≌S4.

图1

考虑图Γ的全自同构群Aut(Γ)在其顶点集V(Γ)上的作用(本文记作Aut(Γ)↘V(Γ)).如果两个顶点v,u∈V(Γ)同属于一个轨道,即存在一个图自同构σ∈Aut(Γ)使vσ=u,则v与u明显具有相同的度数,即deg(v)=deg(u).如果Aut(Γ)↘V(Γ)传递,即对V(Γ)中任意两点v,u都存在一个图自同构σ∈Aut(Γ)使vσ=u,则称Γ是点传递图.这时Γ是正则图(即所有顶点度数相等).由于图自同构保持边不变,而边与边以及边与点之间的邻接情况又决定了图的结构,即图论性质,因此点传递图每个顶点的图论性质都一样, 这就是图的对称性.Aut(Γ)在顶点集V(Γ)上的作用也可以诱导在边集E(Γ)上的作用,即{v,u}σ∶={vσ,uσ}.如果这个作用是传递的, 则称Γ是边传递图.同样, 边传递图每条边的图论性质都一样, 所以也具有一定的对称性.

值得一提的是,图的点传递性与边传递性之间并没有联系.如图2,Aut(Γ3)=〈(123)(456),(12)(45),(14)(25)(36)〉,Γ3是点传递但不是边传递图,因为它的边{v1,v2}是某个3-圈的边,但边{v1,v4}不是,所以边{v1,v2}不能传到边{v1,v4};Γ4是完全二部图K3,4,Aut(Γ4)=〈(1234),(12),(567),(56)〉.Γ4边传递但不点传递, 因为它不正则.

图2

利用有限群很容易构造点传递图，比如本文用到的Cayley图.

定义1.3[1]设G是有限群,S是G#∶=G{1}的一个自逆子集(即S-1=S)，则以G为顶点集,以{{g,sg}|g∈G,s∈S}为边集定义的图称为G关于S的Cayley图,记作Cay(G,S).

性质1.4[2]设Γ∶=Cay(G,S)是群G关于其子集S的Cayley图.分别记A∶=Aut(Γ),A1是A关于G的单位元1的点稳定子,Aut(G,S)∶={α∈Aut(G)|Sα=S}，则

(1)G的单位元1的邻域N(1)=S;

(2)G的右正则表示R(G) ≤A,因此Γ是点传递图,因而是|S|-度正则图，并且A=R(G)A1,R(G)∩A1=1;

(3) Aut(G,S)=Aut(G)∩A≤A1，进而Aut(G,S)正规化R(G);

(4)Γ连通当且仅当G=〈S〉.

V(Qk)∶=V(k,2),E(Qk)∶={{v,εi+v}|v∈V(k,2),εi∈S}.

由于S-1=S且〈S〉=V(k,2),因此Qk是2k阶k-度连通无向图.图3中的两个图分别是2-,3-立方图.

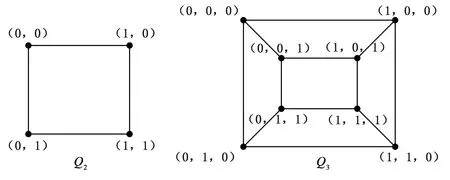
图3

比点传递和边传递条件更强的是弧传递条件.

定义1.6每条无向边{v,u}可看作是由一对方向相反的有向边(v,u)与(u,v)组成,因此无向图Γ的边集也可看作是由一对对方向相反的有向边组成.这时的有向边又称为弧,弧集记作Arc(Γ).如果Aut(Γ)诱导作用在弧集Arc(Γ)上传递,则称Γ是弧传递图.

根据定义,弧传递图明显是点传递和边传递的,但反之不然.例如图2的点传递图Γ3和边传递图Γ4都不是弧传递的.

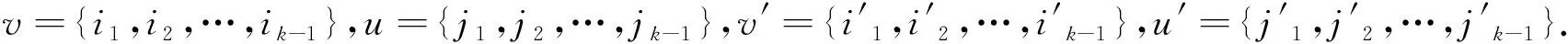
显然(v,u)σ=(v′,u′).由于置换σ把Ω的不相交的(k-1)-元子集仍变为不相交的(k-1)-元子集,因此σ保边,即σ∈Aut(Ok),从而Ok是弧传递的.

图4是2-,3-度奇图O2和O3.

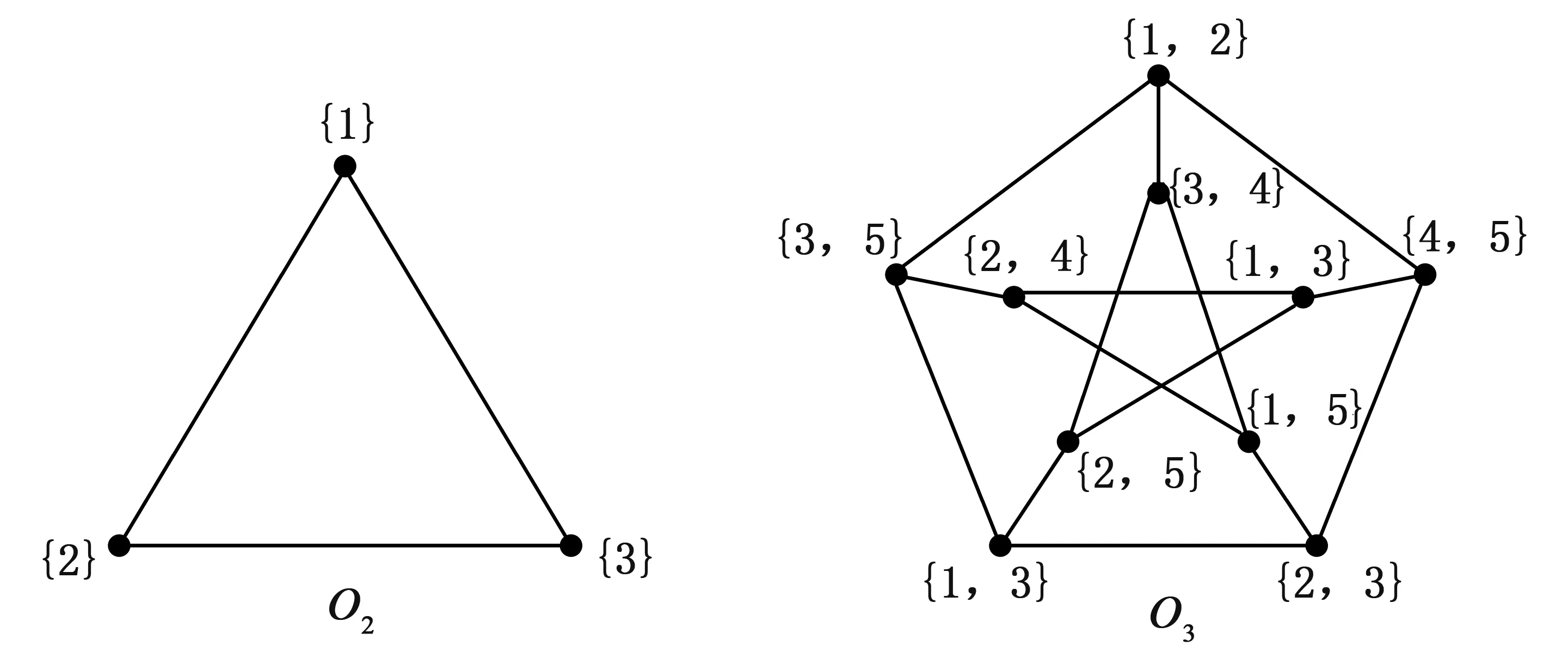
图4

需要提醒读者的是,k-立方图Qk和k-度奇图Ok都是有限传递图中较具代表性的.

接下来引入本文用到的偶圈(圈长为偶数)对边集的概念.

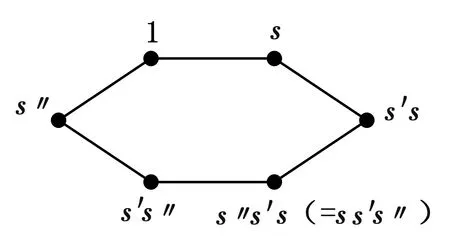
定义1.8设Γ是无向图,l=2k≥4是偶数.如果经过边{v0,v1}∈E(Γ)存在一个l-圈[v0,v1,…,vk-1,vk,vk+1,…,vl-1,vl=v1](见图5),则称边{vk,vk+1}是边{v0,v1}的l-圈对边.

图5

如果E(Γ)的一个包含边{v,u}的子集当且仅当包含边{v′,u′}时包含{v′,u′}的l-圈对边,则称该子集为边{v,u}的l-圈对边集,记作El(v,u).

注:(1) 若经过边{v,u}无l-圈,则El(v,u)={{v,u}};(2) {v′,u′}∈El(v,u)⟺El(v′,u′)=El(v,u).

例1.9观察可知,图2中Γ3的4-圈对边集共有4个,分别是E4(v1,v2)={{v1,v2},{v4,v5}},E4(v1,v3)={{v1,v3},{v4,v6}},E4(v2,v3)={{v2,v3},{v5,v6}}和E4(v1,v4)={{v1,v4},{v3,v6},{v2,v5}};而图Γ4的6-圈对边集只有1个,即E6(v1,v5)=E(Γ4).

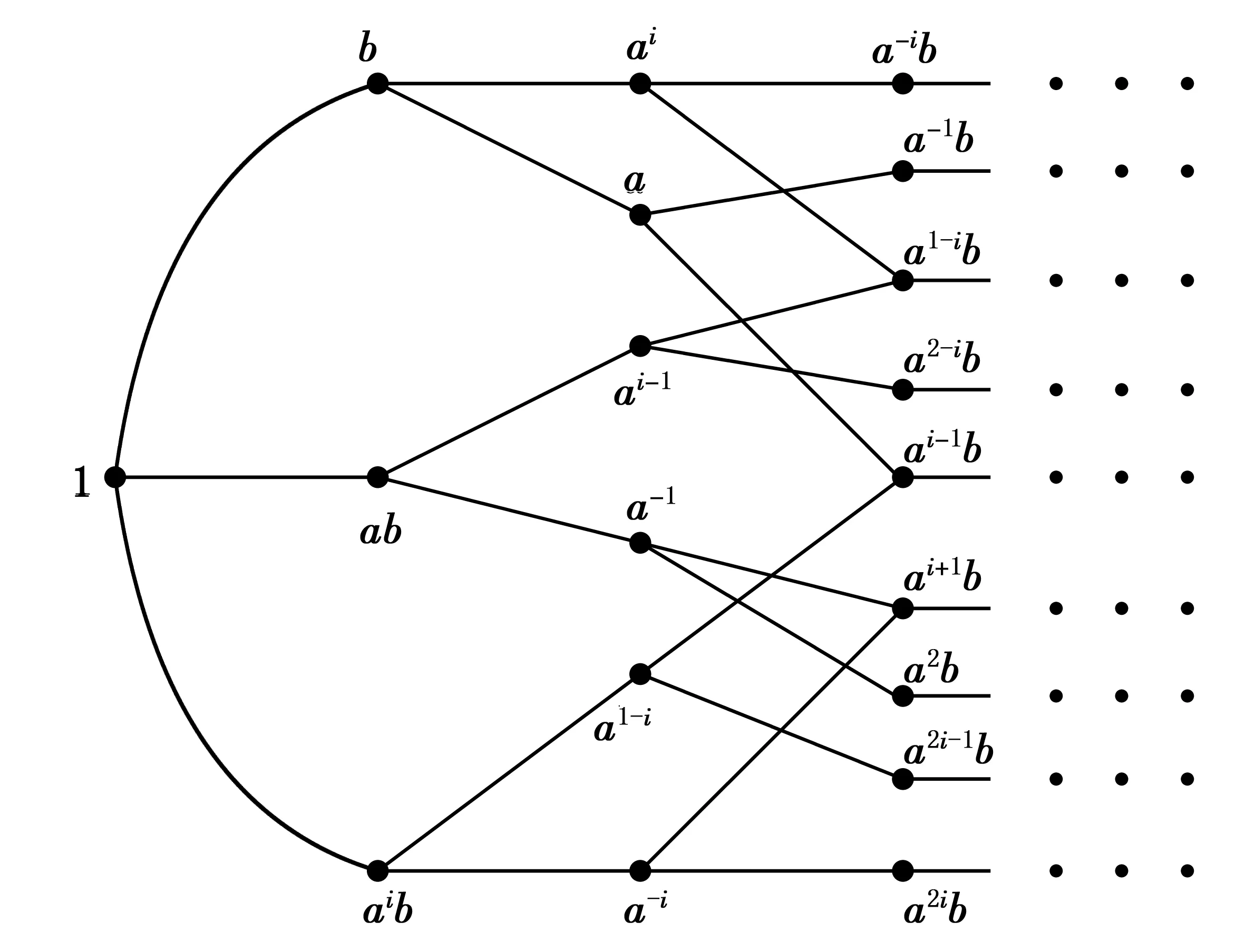
例1.10试决定k≥ 2-立方图Qk的4-圈对边集.

解任取{v,u}∈E(Qk).沿用例1.5的记号,则u=v+εi,其中εi∈S.然而经过边{v,u}的4-圈只能是[v,u,u+εj,v+εj,v],其中εj∈S,j≠i.说明边{v+εj,u+εj}是边{v,u}的4-圈对边,即{v+εj,u+εj}∈E4(v,u).根据偶圈对边集的定义,当边{v′,u′}∈E4(v,u)时,有∀ε∈S,边{v′+ε,u′+ε}∈E4(v,u).再由V(k,2)是S生成的加群,即知E4(v,u)={{v+w,u+w}|w∈V(k,2)}.

例1.11试决定k≥3-度奇图Ok的6-圈对边集.

解先证Ok连通,即证Ok的任意两顶点v与u之间存在一条路.为此,对|v∩u|=i0.取v′∶={1,2，…,k-1},u′∶={k+1,k+2,…,2k-1}∈V(Ok)，则{v,u′},{v′,u′}∈E(Ok)，再由|v′∩u|=i-1及归纳假设得,v′与u之间存在一条路, 因此v与u之间也存在一条路.即Ok是连通图.

然后决定Ok的6-圈对边集.任取{v,u}∈E(Ok).根据奇图的构造知,存在唯一的i∈Ω(v+u).由此可定义E(Ok)到Ω的映射f,使f(v,u)=i.显然,f(v,u)=f(v,u).以下证明Ok具有下述的一些性质,也决定其边的6-圈对边集.

(1) 若[v0,v1,v2]是2-路,则v0∪v2⊆Ωv1且f(v0,v1)≠f(v1,v2).

图6

图7

事实上, 由v0≠v2及Ω=v0+v1+{f(v0,v1)}=v1+v2+{f(v1,v2)},即知结论成立.

(2)Ok没有3-圈.

事实上,由(1)知任意2-路[v0,v1,v2]首尾的并集v0∪v2Ωv1，因此|v0∪v2|≤k.利用公式|v0|+|v2|=|v0∪v2|+|v0∩v2|及|v0|=|v2|=k-1,推出2k-2≤k+|v0∩v2|，因此|v0∩v2|≥k-2>0,即{v0,v2}∉E(Ok),说明Ok没有3-圈.

(3) 设[v0,v1,v2,v3]是Ok的一条3-路，则f(v1,v2)∈v0∩v3.

事实上,由(1),f(v1,v2)≠f(v2,v3)以及f(v1,v2)∈Ω(v1+v2)Ωv2=v3+{f(v2,v3)},即得f(v1,v2)∈v3.同理,f(v1,v2)=f(v2,v1)∈v0.(3)得证.

(4)Ok没有4-圈.

事实上,由(3)知任一条3-路[v0,v1,v2,v3]的首尾v0,v3有交,即{v0,v3}∉E(Ok),导致Ok没有4-圈.

(5)Ok存在5-圈当且仅当k=3.

v0Ωv1v2+{f(v1,v2)},v4Ωv3v2+{f(v2,v3)}.

再由v0∩v4=Ø及f(v1,v2) ≠f(v2,v3),推出v0+v4v2+{f(v1,v2)}+{f(v2,v3)}.比较两边的阶,得2k-2=|v0+v4|≤|v2|+2=k+1，因此k≤3,但只能有k=3.

(5)得证.

(6) 经过任一条3-路[v0,v1,v2,v3]有且仅有一个6-圈,并且圈上的每对对边都取相同的f值.

先证存在性.由v1∩v2=Ø及(3)有，f(v2,v3)∈v1,f(v0,v1)∈v2，从而f(v2,v3)≠f(v0,v1).于是可取与v3连边的顶点v4=Ω(v3+ {f(v0,v1)})∈V(Ok).而由f(v1,v2)∈v3=v3v4,又可取与v4连边的顶点v5=Ω(v4+{f(v1,v2)})∈V(Ok).这时,

f(v0,v1)=Ω(v3+v4)=f(v3,v4),f(v1,v2)=Ω(v4+v5)=f(v4,v5).

(1.1)

由于Ok无3-,4-圈,因此[v0,v1,v2,v3,v4,v5]是一条5-路(见图8).

图8

往证v0∩v5=Ø且v0∪v5=v2∪v3.事实上,由Ω=v0+v1+{f(v0,v1)}=v1+v2+{f(v1,v2)}，有v0+{f(v0,v1)}=v2+{f(v1,v2)},由此得

v0={f(v1,v2)}+v2{f(v0,v1)}.

(1.2)

而由Ω=v4+v5+{f(v4,v5)}=v3+v4+{f(v3,v4)}有v5+{f(v4,v5)}=v3+{f(v3,v4)},又得

v5={f(v3,v4)}+v3{f(v4,v5)}={f(v0,v1)}+v3{f(v1,v2)}.

(1.3)

由于f(v1,v2)≠f(v0,v1)及v2∩v3=Ø,故从(1.2)与(1.3)二式可推出v0∩v5=Ø且v0∪v5=v2∪v3.

至此,得{v0,v5}∈E(Ok),即[v0,v1,v2,v3,v4,v5,v0]是6-圈,并经过3-路[v0,v1,v2,v3](见图9).

图9

再由(1.1)及f(v0,v5)=Ω(v0∪v5)=Ω(v2∪v3)=f(v2,v3),知圈上的每对对边都取相同的f值.

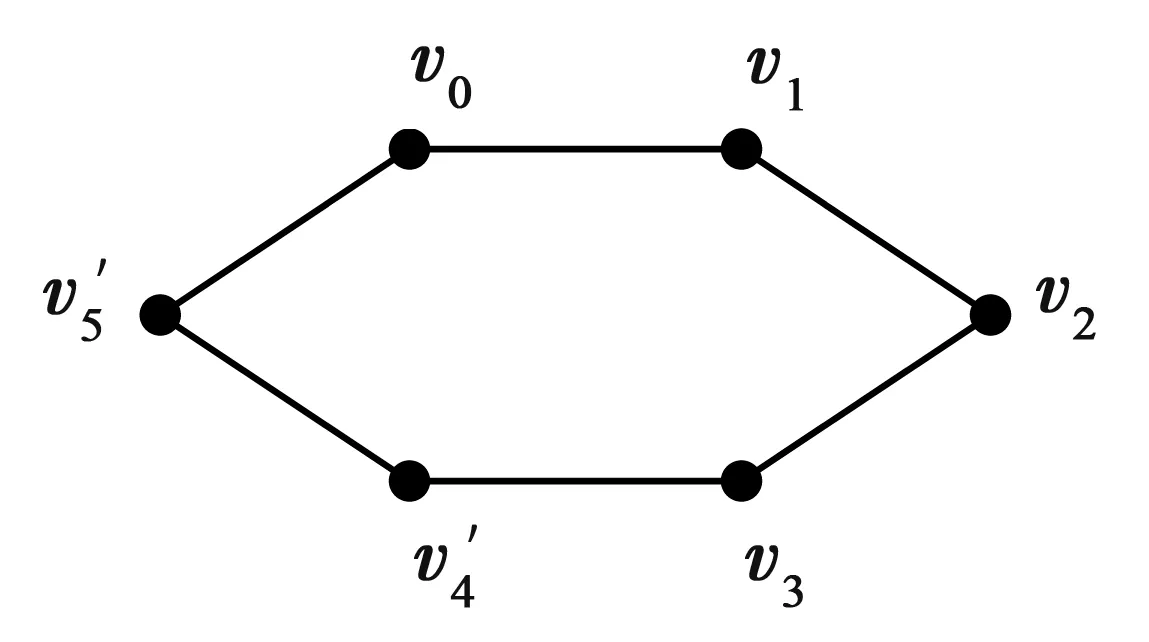
图10

(7) 边{v,u}∈E(Ok)的6-圈对边集E6(v,u)={{v′,u′}|f(v′,u′)=f(v,u)}.

由(6)及Ok的连通性即可证(7)成立.

偶圈对边集明显具有图论性质, 它在研究图的对称性时可发挥关键作用. 本文利用偶圈对边集的图论性质证明了具有6-圈的某些二面体群Cayley图的正规性. 偶圈对边集的概念也很新颖, 涉及的是图的传递性问题, 运用的是抽象群的理论.

本文引入的概念和记号大都是通用的, 对于未定义而引用的概念和记号, 读者可查阅文献[2,3].

2 预备知识

先介绍一些本文用到的概念、性质和结论.

性质2.2[2]Γ正规当且仅当A1=Aut(G,S).

引理2.3[2]设Γ∶=Cay(G,S)是有限群G的Cayley图.若|Aut(Γ)1|≤2,则Γ是正规Cayley图.

引理2.4[4]设Γ∶=Cay(G,S)是连通3-度非弧传递Cayley图,则Γ正规当且仅当Aut(Γ)1诱导作用在S上忠实.

引理2.5[5]设Γ∶=Cay(G,S)是有限交换群G的连通Cayley图.若S的任意两个非互逆二元子集{s1,s2}与{s3,s4}在s1s2=s3s4时相等,则Γ是正规Cayley图.

定义2.6在Cayley图Cay(G,S)中,由s1,s2,…,sl∈S组成的序列(s1,s2,…,sl)称为G的S-序列.如果s1,s2,…,sl∈S可生成以某顶点g∈G为起点的l-路(圈)[g,s1g,s2s1g,…,sl…s2s1g],则称(s1,s2,…,sl)为G的对应于该路(圈)的强S-序列.

由定义2.6易知

性质2.7S-序列(s1,s2,…,sl)是强S-序列的充要条件是，∀l≥j>i≥1,j-i

例2.8设Γ∶=Cay(G,S).若S中含有l>2阶元s,则Γ存在l-圈Cl.

证明显然,[1,s,s2,…,sl-1,sl=1]是Γ的l-圈Cl.而(s,s,…,s)(l个分量)是对应于该圈的强S-序列.

引理2.9设Γ∶=Cay(G,S).若s≠s′∈S可交换但不互逆,则Γ存在4-圈.

证明由s′s=ss′即知[1,s,s′s,s′,1]是Γ的4-圈.而(s,s′,s-1,s′-1)是对应于该圈的强S-序列.

引理2.10[2]图Γ弧传递的充要条件是Γ点传递且A∶=Aut(Γ)关于v∈V(Γ)的点稳定子群Av诱导作用在N(v)上传递.

定义2.11设Γ是简单图,K≤Aut(Γ).子集△V(Γ)称为K的不变区或K-不变区,如果△K△.对于只含一个元素的不变区,该元素称为不动点.特别地,当K=〈α〉时,〈α〉-不变区简称α-不变区,〈α〉-不动点则简称α-不动点.

引理2.12[6]设Γ∶=Cay(G,S)是群G的Cayley图,s∈S是A∶=Aut(Γ)关于1的点稳定子A1的不动点，则

(1) ∀α∈A,g∈G,sgα=(sg)α,(g,sg)α=(gα,sgα);

(2)A≤Aut(Cay(G,S{s}));

(3) ∀v∈V(Γ),svSv=N(v)是Av-不动点.特别地,当v∈N(1)=S时,sv是A1作用在N(1)上的核的不动点.

证明(1) 易知R(g)αR[(gα)-1]∈A1,因此s=sR(g)αR[(gα)-1]=(sg)α(gα)-1，于是sgα=(sg)α.进而(g,sg)α=(gα, (sg)α)=(gα,sgα).

(2) 设α∈A,s′∈S{s}，则由(1)知,(gα,sgα)=(g,sg)α≠(g,s′g)α=(gα,s″gα),由这推出s″∈S{s},即得α∈Aut(Cay(G,S{s})).

(3) ∀α∈Av,由(1)即得(sv)α=svα=sv.

引理2.13[2]若Cayley图Γ∶=Cay(G,S)连通,则|Aut(Γ)1|没有大于|S|的素因子.

证明用反证法.若有素数p>|S|且p||A1|,则A1含p阶元α.由于素数阶循环群〈α〉↘N(1)的轨道长只能是1或p,但不能是p(否则与|N(1)|=|S|

由引理2.13显然有

推论2.14记号及条件同引理2.13,并设△是含于S的阶最大的Aut(Γ)1-不变区,则|Aut(Γ)1|没有大于|△|的素因子.

推论2.15[6]3-度或4-度连通Cayley图Γ的点稳定子Aut(Γ)1是{2,3}-群.

3 主要结论

定理3.1设G是有限交换群,S=S-1G#(不必生成G),s∈S,则Cayley图Γ∶=Cay(G,S)满足:

(1) 经过边{1,s}至少有|S{s±1}|个4-圈;

(2)S的任意两个非互逆二元子集{s1,s2}与{s3,s4}在s1s2=s3s4时相等，则经过边{1,s}只有|S{s±1}|个4-圈;

(3) 经过边{1,s}只有│S{s±1}│个4-圈，则|E4(1,s)|=│〈S{s±1}〉│.

证明(1) 任取s′∈S{s±1},则(s,s′,s-1,s′-1)是一组强S-序列,并生成经过边{1,s}的一个4-圈[1,s,s′s,s′,1](见图11).因此经过边{1,s}至少有│S{s±1}│个4-圈.

图11

图12

(3) 由(1)及题设可知,经过边{1,s}的4-圈只能由s和s′∈S{s±1}做成的强S-序列(s,s′,s-1,s′-1)生成.这时,边{s′,ss′}={1,s}R(s′)恰是边{1,s}的一条4-圈对边,即{1,s}R(s′)∈E4(1,s)(见图13).任取s″∈S{s±1},则(s,s″,s-1,s″-1)也是一组强S-序列,它可生成由s′出发并经过边{s′,ss′}的一个4-圈[s′,ss′,s″ss′,s″s′,s′](见图13).这时,边{s″s′,s″ss′}={s′s″,ss′s″}={s′,ss′}R(s″)恰是边{s′,ss′}的4-圈对边,因此也有{s′,ss′}R(s″)={1,s}R(s′s″)∈E4(1,s),并且s′s″∈〈S{s±1}〉.

图13

由此可知E4(1,s)中的边形如{v,sv},其中v∈〈S{s±1}〉.往证,当E4(1,s)包含边{v,sv}时,对于任意s′∈S{s±1},边{v,sv}R(s′)恰是边{v,sv}的4-圈对边.事实上,利用强S-序列(s,s′,s-1,s′-1)可生成经过边{v,sv}的一个4-圈[v,sv,s′sv,s′v,v](见图13).而边{s′v,s′sv}={vs′,svs′}={v,sv}R(s′)正是边{v,sv}的一条4-圈对边,因此{v,sv}R(s′)∈E4(1,s).

上述事实等价于E4(1,s)={{1,s}R(g)|g∈〈S{s±1}〉},即证明了(3).

例3.2k-立方图Qk满足定理3.1的条件,因此是正规Cayley图,并且经过每条边都恰有k-1个4-圈.

证明沿用例1.5的记号并利用其结论,则k-立方图Qk是Cayley图Cay(G,S),其中G是加群V(k,2),S={ε1,ε2,…,εk}.若S的任意两个非互反二元子集{εi1,εi2}和{εi3,εi4}满足εi1+εi2=εi3+εi4,则εi3+εi4只有第i1和第i2这两个分量是1,其余分量是0,由此推出{εi1,εi2}={εi3,εi4}.即Qk满足定理3.1的条件.再由Qk的点传递性及引理2.5,即知Qk是正规Cayley图.这时,经过Qk的每条边都恰有|S|-1=k-1个4-圈.比如,经过Q2的每条边都恰有1个4-圈,经过Q3的每条边都恰有2个4-圈.

定理3.3取2n阶二面体群G∶=〈a,b|an=b2=1,b-1ab=a-1〉的4-元自逆子集S∶={ai,a-i,ajb,b},其中j≠±i,±2i,n/2，则4-度Cayley无向图Γ∶=Cay(G,S)满足:

(1) 经过边{1,b}和边{1,ajb}各有2个4-圈,并且|E4(1,b)|=|E4(1,ajb)|=o(ai);

(2) 经过边{1,ai}和边{1,a-i}各有2个4-圈,并且|E4(1,ai)|=|E4(1,a-i)|=2o(aj).特别地,当o(ai)≠2o(aj)时,{ai,a-1}和{ajb,b}都是Aut(Γ)1-不变区;

证明(1) 取两组强S-序列(b,ai,b,ai)和(b,a-i,b,a-i),即可构造经过边{1,b}的2个4-圈[1,b,aib,a-i,1]和[1,b,a-ib,ai,1].同理,经过边{1,ajb}也有2个4-圈[1,ajb,aj+ib,a-i,1]和[1,b,aj-ib,ai,1].由此,过顶点1恰有4个4-圈,并可组成一个“田”字.再由Cayley图的点传递性,可得Γ的一个局部如图14(距离超过4的顶点可能重复, 但不影响证明).

容易看出,导出子图[〈ai〉∪b〈ai〉]同构于梯图Co(ai)×K2,而边{1,b}的4-圈对边集E4(1,b)中的边恰是该梯图的所有“阶梯”,因此E4(1,b)={{1,b}R(g)|g∈〈ai〉}.同理,E4(1,ajb)={{1,ajb}R(g)|g∈〈ai〉}.从而|E4(1,b)|=|E4(1,ajb)|=o(ai).

(2) 由图14即知经过边{1,ai}和边{1,a-i}也各有2个4-圈.此外,图自同构R(a-ib)把边{1,ai}变到其4-圈对边{1,ai}R(a-ib)={b,a-ib};而图自同构R(aj)把边{1,ai}变到{b,a-ib}的4-圈对边{1,ai}R(aj)={aj,aj+i}.因此,{1,ai}R(a-ib),{1,ai}R(aj)∈E4(1,ai).进一步,图自同构R(a-j-ib)把边{1,ai}变到{aj,aj+i}的4-圈对边{1,ai}R(a-j-ib)={a-jb,a-j-ib};而图自同构R(a2j)把边{1,ai}变到{a-jb,a-j-ib}的4-圈对边{1,ai}R(a2j)={a2j,a2j+i}.因此,{1,ai}R(a-j-ib),{1,ai}R(a2j)∈E4(1,ai).如此继续下去,可推出E4(1,ai)={{1,ai}R(g)|g∈〈aj〉∪〈aj〉a-ib}.同理,E4(1,a-i)={{1,a-i}R(g)|g∈〈aj〉∪〈aj〉aib}.从而,|E4(1,ai)|=|E4(1,a-i)|=2o(aj).事实上,E4(1,ai)和E4(1,a-i)中的边也分别是两个都同构于C2o(aj )×K2的梯图的“阶梯”.

由于偶圈对边集的阶是图论性质, 故当o(ai)≠2o(aj)时,Aut(Γ)1显然不能在{ai,a-1}与{ajb,b}之间互变顶点, 由此{ai,a-1}和{ajb,b}都是Aut(Γ)1-不变区.

图14

(4) 由题设,易知〈S〉=〈aib,ajb〉=G,并且o(ai)≠2o(aj).再由(3)和(2),即知A1是作用在N(1)上忠实的2-群,并且{ai,a-1}和{ajb,b}都是A1-不变区.进而由推论2.14,A1只含对合,因此是阶整除4的初等交换2-群.

(3.1)

先证β是良定义的,即当g∈btakj〈ai〉∩btak′j〈ai〉(t∈{0, 1})时, 根据映射关系(3.1),理应有

gβ=btg-1bta2kj=btg-1bta2k′j.

(3.2)

事实上,由g=btakj+li=btak′j+l′i，有(k-k′)j≡(l′-l)i(modn)，于是i|k-k′，故2(k-k′)j≡0(modn),说明(3.2)成立,即β是良定义的.其次证β是A1中异于α的对合.已有1β=1，再由(akj+li)β2=(akj-li)β=akj+li，(bakj+li)β2=(bakj-li)β=bakj+li，即知β是对合.

再证β保边,即∀g∈G,s∈S={ai,a-i,ajb,b},往证(gβ,(sg)β)=(gβ,s′gβ),s′∈S,或证(sg)β(gβ)-1∈S.以下分4种情况证明.

情况1s=ai

若g=akj+li∈akj〈ai〉,则sg=akj+li+i,(sg)β(gβ)-1=(akj+li+i)β[(akj+li)β]-1=akj-li-i(akj-li)-1=a-i∈S.

若g=bakj+li∈bakj〈ai〉,则sg=bakj+li-i,(sg)β(gβ)-1=(bakj+li-i)β[(bakj+li)β]-1=bakj-li+i(bakj-li)-1=bakj-li+i(a-kj+lib)=ai∈S.

情况2s=a-i

证明类似情况1,略.

情况3s=ajb

若g=akj+li∈akj〈ai〉,则

sg=ba(k-1)j+li∈ba(k-1)j〈ai〉,

(sg)β(gβ)-1=(ba(k-1)j+li)β[(akj+li)β]-1=ba(k-1)j-li(akj-li)-1=ajb∈S.

若g=bakj+li∈bakj〈ai〉,则

sg=a(k+1)j+li,

(sg)β(gβ)-1=(a(k+1)j+li)β[(bakj+li)β]-1=a(k+1)j-li(bakj-li)-1=a(k+1)j-li(a-kj+lib)=ajb∈S.

情况4s=b

若g=akj+li∈akj〈ai〉,则

sg=bakj+li∈bakj〈ai〉,(sg)β(gβ)-1=(bakj+li)β[(akj+li)β]-1=bakj-li(akj-li)-1=b∈S.

若g=bakj+li∈bakj〈ai〉,则

sg=akj+li∈akj〈ai〉,

(sg)β(gβ)-1=(akj+li)β[(bakj+li)β]-1=akj-li(bakj-li)-1=akj-li(a-kj+lib)=b∈S.

至此证明了β是A1中对合.再由β不动顶点b,可得β≠α.进而A1=〈α,β〉=2×2,即|A1|=4.只需证,假设2ij≢0(modn),则A1=〈α〉.任取则σ只能是对合.以下分两种情况讨论.

情况1σ不动b

情况2bσ=ajb

特别地,当2ij≢0(modn)时,由上述证明知|A1|=2.再由引理2.3,即知Γ是正规Cayley图.

定理3.4设二面体群G∶=〈a,b|an=b2=1,ab=a-1〉,S是G的元素不少于3个且都形如aib的子集(不必生成G).记Γ∶=Cay(G,S),A∶=Aut(Γ),k=|S|-1,并取s∈S，则

(1)Γ=[〈a〉,〈a〉b]是二部图,即Γ的每条边都有且仅有一个端点含于〈a〉;

(4) 当S={aib,ab,b},3

(5) 当n=2ip,i≥2,p是奇素数,S={apb,a2jb,a2j(2p2-1)b,b},1≤j≤i时,Γ是正规Cayley图,并且|A1|=2.

证明(1) 显然(证略).

图15

(3) 由(2)及题设可知,经过边{1,s}的6-圈就只能由s和s′≠s″∈S{s}做成的强S-序列(s,s′,s″,s,s′,s″)生成.这时,边{s′s″,ss′s″}={1,s}R(s′s″)恰是边{1,s}的一条6-圈对边,即{1,s}R(s′s″)∈E6(1,s).并且{1,s}的6-圈对边形如{v,sv},其中v∈〈a〉(见图15).

往证,当E6(1,s)包含边{v,sv}(v∈〈a〉)时,∀s′≠s″∈S{s},边{v,sv}R(s′s″)恰是边{v,sv}的6-圈对边,并且vR(s′s″)∈〈a〉.事实上,利用强S-序列(s,s′,s″,s,s′,s″)可生成经过边{v,sv}的一个6-圈(见图16).