高等数学教学中转化思想的应用
王秀红,李美凤
(天津商业大学 理学院,天津 300134)
1 引言
转化思想是分析问题和解决问题常用的一种重要数学思想,具体是指在处理问题时,将未知解法或难以解决的问题,通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为已知知识范围内已经解决或容易解决的问题,最终求得原问题的解[1]。
在高等数学中,有很多内容都体现了转化思想。下面从几个方面对转化思想的应用进行举例探析。
2 复杂化简单
在求函数极限时,用无穷小量代换极限式中的函数表达式是简化极限计算过程的一种方法。

3 特殊化基本
(3)1∞,00,∞0这三类未定式,由于都来源于幂指函数u(x)v(x)的极限,所以均可以通过恒等变形:
u(x)v(x)=ev(x)lnu(x)


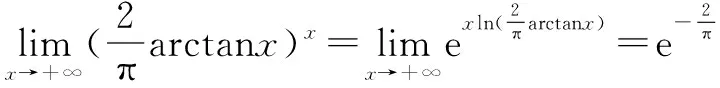
4 未知化已知
基本积分公式是求不定积分的基础,而仅仅靠基本积分公式和不定积分的性质来解决不定积分的计算问题是远远不够的,还需要更有效的积分方法。换元积分法就是在积分过程中通过转化思想引入新变量,来简化积分计算的一种积分方法[2]。
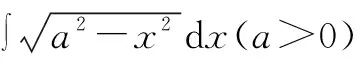
解:为了将被积函数中的根号去掉,
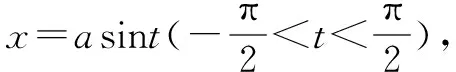
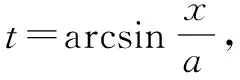
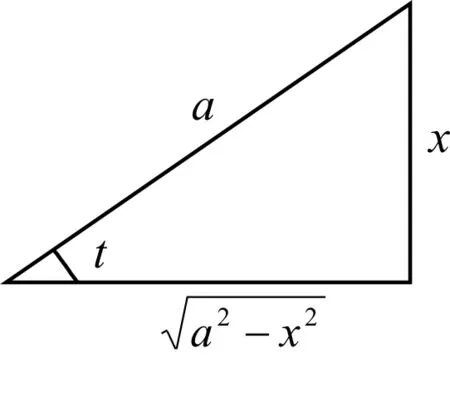
图1 三角形的边角关系
5 数化形
根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题,实现数形结合。
例4 方程x2+y2+z2-2x+6y-4z=0表示什么曲面?并判断点P(1,1,1)与此曲面的位置关系。
解:将方程配方变形为:
(x-1)2+(y+3)2+(z-2)2=14

(1-1)2+(1+3)2+(1-2)2=17>14
所以点P(1,1,1)在球面外。
6 高维化低维
利用二重积分的定义计算二重积分难度很大,因此需要寻求一些更为有效的计算方法。实际上,可利用降维的思想加以研究,即:将二维平面上的二重积分化为两个一维区间上的定积分(即累次积分),利用定积分来计算。
解:积分区域D(图2)表示如下:
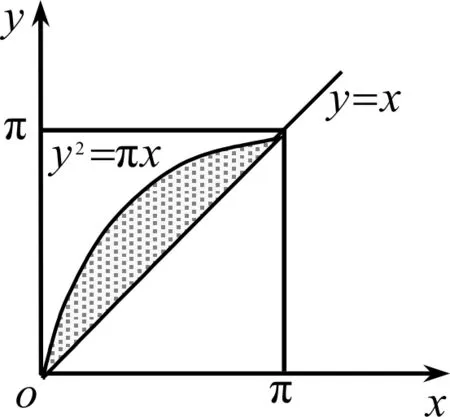
图2 积分区域D

=-(-1)+1-1=1
7 直接化间接
把一个已知函数展开为幂级数,固然可以应用直接展开法.但更多的情况是根据函数幂级数展开式的唯一性,借助已知函数的泰勒展开式,通过变量代换、四则运算、恒等变形、逐项求导和逐项积分等转化思想,利用间接展开法来求另一些函数的幂级数展开式.当然,使用间接展开法需要熟悉一些常用的幂级数展开式。


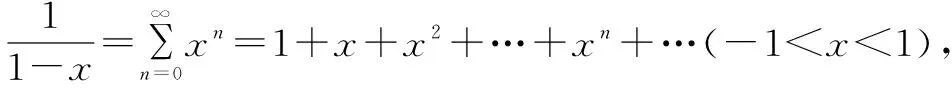
8 常量化变量
常数变易法是求解一阶线性非齐次常微分方程的重要方法,即将常数变易为待定函数,通过求解待定函数的表达式进而求出原方程的通解。
解:此方程为一阶线性非齐次微分方程。首先,求出一阶线性齐次微分方程
的通解为y=Cx2
其次,利用常数变易法求一阶线性非齐次微分方程的通解。将常数C变易为待定函数C(x),即令
y=C(x)x2,将其带入原方程后可以得到
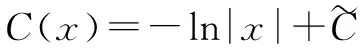
从而,原方程的通解为:

9 结语
转化思想就像一把神奇的金钥匙,对解放思想,开阔思路,解决某些难题,开创新的方向,起到了积极的作用[3]。 整个高等数学的教学过程中转化思想的运用层出不穷,需要不断巩固知识,发现总结才能正确利用转化思想。因此,在教学过程中应注重渗透这种思想方法,重视培养学生的转化思维能力,培养创新能力,激发学生的学习热情。

