基于离港航班密度区间划分的动态推出控制方法

廉冠, 李彪, 王涛, 李文勇

(1. 桂林电子科技大学 建筑与交通工程学院，广西 桂林 541004；2. 中国民航大学 航空工程学院，天津 300300) *

飞机的离港由申请推出、同意推出、推出、滑行(滑行道排队等待)、跑道端头等待、起飞等过程组成，其中滑行至起飞过程需要一定量的燃油消耗，在大型枢纽机场，尤其在离港高峰期，飞机往往要经历长时间的滑行道排队等待，导致离港燃油成本和排放的增加.在不新建或扩建机场增加机场资源量的前提下，通过寻找合理的推出控制方法来减少燃油消耗和排放已成为当前的研究热点.Carr等[1]提出了一种推出控制方法提前对推出航班进行排序，并用蒙特卡洛方法对波士顿机场离港数据进行仿真验证.Roling等[2]开发了一种飞机地面滑行支持工具，这种工具通过地面运行里程碑时刻来预计推出时刻，以降低离港延误时间.Feron等[3]提出了N-control推出控制方法来控制离港飞机的推出频率，这种方法允许飞机在停机位等待一段时间并通过找寻最优推出频率来降低滑行燃油消耗.Pujet等[4]利用N-control的方法建立了一种动态离港排队模型，该模型可以使飞机在少量延误的前提下降低离港成本，并且提出研究更先进的控制方法可以达到更高的离港效率，为N-control方法的研究指明了方向.Bertsimas等[5]使用整数规划的方法对机场地面交通流进行建模，旨在优化停机位等待时间和路径规划问题.Menon等[6]针对机场地面交通流量控制问题，提出了一种空间聚合技术来模拟交通模式，利用反馈性线性控制分析法确定最优推出频率.Simaiakis等[7]将离港过程视为多阶段串联排队过程，以离港总成本为目标，在对排队模型进行马尔科夫分析的基础上，使用动态规划方法对模型寻优并找出最适合的推出频率表达式.Martinez等[8]进一步对N-control控制方法进行分析，考虑了包括运行效率、运行成本及机场管制等因素，在保证机场吞吐量的前提下调节推出频率.张亚平等[9]分析了N-control方法的静态控制性，提出了这种控制方法的不足，并提出了一种基于惩罚成本的动态频率推出控制方法(DPC方法)，给出了DPC方法的控制率表达式，这种方法的优点是可以根据当前滑行道飞机排队长度实时动态地调节推出率，以减少滑行燃油消耗.Lian等[10]提出了一种基于滑行时间预测的动态推出控制方法，首先对滑行时间进行预测，根据预测结果对滑行道等待时间和停机位等待时间进行合理分配，以达到燃油节省效果.廉冠等[11]对动态推出控制方法进行改进，提出两种扩展方法，并提出一种基于网格参数优化的蒙特卡洛仿真优化方法对离港模型进行寻优.

在传统N-control推出控制模型和现有的DPC方法中，N值一般根据离港高峰期流量来确定，它并不随离港航班的密度进行变化，推出控制系统的“开关”即被决定，在离港低峰流量时段，N-control控制方法便失去了作用.然而，一种合理的推出控制方法应当能根据不同时段的航班流量来调节滑行道队长阈值，以适应离港实际情况.为改进滑行道队长阈值恒定所带来的经济损失、减少推出方法失效的情况，本文提出一种基于离港航班密度划分的动态推出控制模型，以进一步减少滑行时间及燃油消耗.

1 飞机离港推出控制模型

为了方便本文的模型描述，变量索引如下：

模型变量：

X—推出请求集合；E—推出请求时间段总数；l—推出请求时间段长度；d—离港高低峰期分界线；λ—推出率；μ—平均服务时间；j—推出飞机索引，j=1,2,…；c—每架飞机滑行燃油消耗成本/min;G—停机位等待时间阈值；M—推出请求总数；θ—停机位等待惩罚参数；CT—离港总成本.

状态变量:

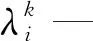
决策变量：

Ki—时间段i内滑行道排队程度阈值.

1.1 动态推出控制模型

如图1所示，飞机在停机位(登机口)进行旅客登机，然后向塔台申请推出，待塔台同意推出，由牵引车推出后打开APU进行滑行，当离港飞机密度较高时，在滑行道上会形成排队.由于滑行过程需消耗燃油，因此控制模型的思想是当滑行道排队长度较大时，塔台将暂时驳回推出申请，使飞机在停机位停留一段时间后重新申请推出，进而节省燃油，然而这样做会导致停机位使用效率降低，因此这里给予一个与停机位等待时间呈正相关的惩罚因子.

图1 离港动态推出控制流程图

动态推出控制模型可以进行如下表示：

(1)

动态推出控制的特点是推出率可以随当前滑行道等待队列长度实时变化，当k值增加时，推出率会减小，反之亦然.当推出申请被拒绝时，飞机需在停机位等待一段时间重新进行推出申请.而为了平衡停机位等待时间过长而引起的停机位使用效率下降，文献[11]提出了一种停机位等待惩罚成本计算方法，然而，其提出的惩罚计算方法有较大缺陷，例如当停机位等待时间较小时，对停机位等待航班直接进行收费显然不合理，惩罚的目的应该是鼓励短时等待而非长时间等待.因此，本文修正惩罚函数计算方法为指数函数形式，记为(eβE[gj]-1)因此，动态推出控制模型可以记作：

(2)

(3)

(4)

0≤k≤K

(5)

gi≤30

(6)

其中:式(2)为目标函数，即总离港成本；约束(3)为每个时间段内的最小成本；式(4)为申请飞机数量约束；式(5)为滑行道排队长度约束；式(6)为停机位等待时间约束.问题的目标是总成本，核心指标为各个时间段的滑行道排队长度阈值Ki.

1.2 离港航班时间段划分

以小时为时间段长度单位会降低其多样性，而时间段过短会导致滑行道队长阈值变化频繁而增加操作难度，因此本文以30 min为区间单位进行划分.在理想情况下，如果飞机严格按照起飞间隔(即服务时间)进行推出，则每30 min不产生滑行道排队的推出数量极限为d=⎣30/μ」.然而d为理想情况下的推出数量极限，在实际情况中，往往由于推出时刻分布不均匀而导致排队情况，因此本文将此极限扩展到d=[⎣15/μ」,⎣30/μ」],d∈Ζ+，通过对模型寻优进行最优推出数量极限的确定.

1.3 模型求解

由于模型描述的是一天中所有航班的离港过程，飞机数量较多，而且模型最优目标所对应的参数较多，这为模型的求解带来一定困难.因此本文设计了一种基于航班时段划分和蒙特卡洛法的动态推出过程求解算法，算法流程图如图2所示.

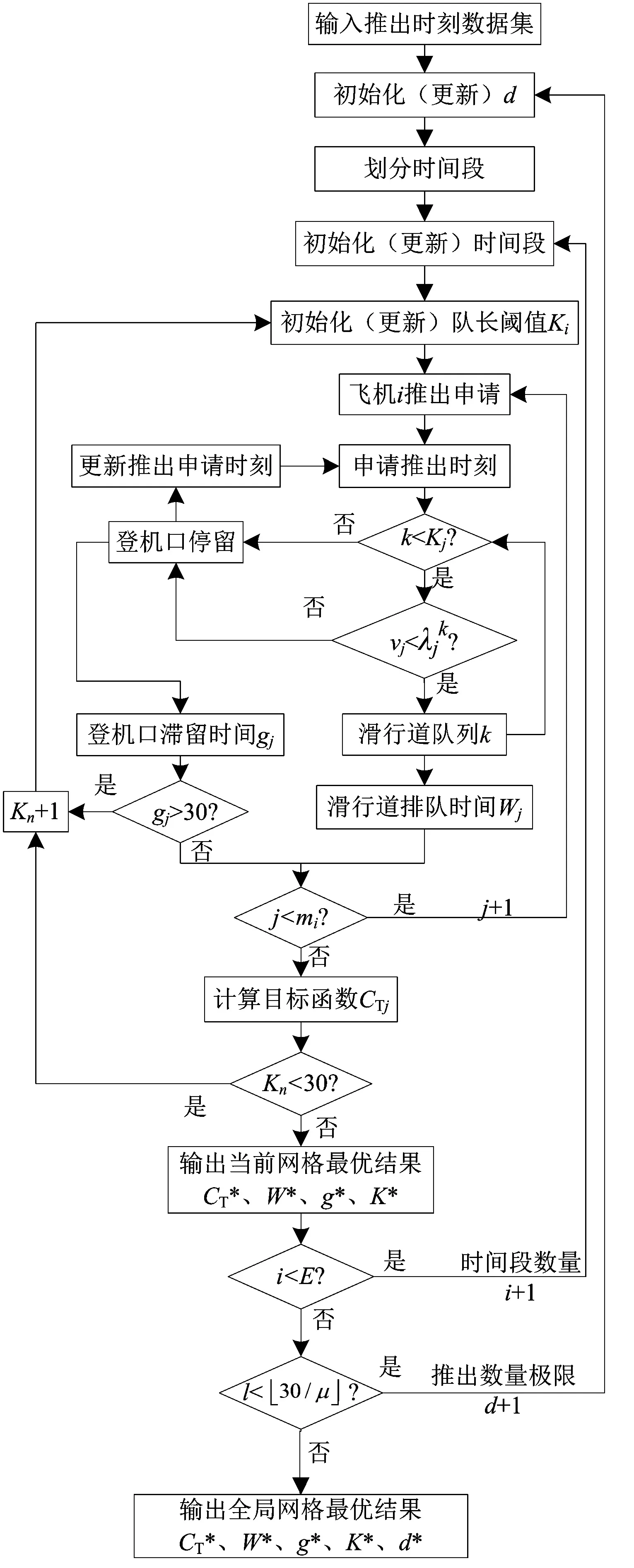
图2 基于航班时段划分和蒙特卡洛法的动态推出过程求解算法

算法包括三层循环，外层为推出数量极限d/每0.5h的循环，中层为d所对应的时间段分区循环，内层为一天内所有航班推出过程所设定滑行道排队长度的循环.在内层循环中，当一架飞机申请推出时，塔台批准推出的条件由两部分组成：传统N-control方法和动态推出的蒙特卡洛法.后者的思想如下：当一架飞机申请推出(或重新申请)时，系统会生成一个随机数v∈(0,1)，当v<(1-k/K)时，拒绝该飞机进行推出，使其停留在停机位等待重新申请，反之则允许推出，然后进入滑行道队列，以此模拟推出频率，每一次内层循环结束，记录W和g的结果，以此类推直到三层循环结束后输出最优成本及其所对应的参数.

2 实例分析

本文利用MATLAB 2018b软件对提出的基于离港航班密度划分的动态推出控制模型进行仿真分析，仿真数据集取自北京首都机场2013年离港数据库，由于离港数据在一段时间内(如一个月)具有相似性，并且在离港飞机密度很小的时段(如凌晨)，推出控制手段便失去意义，因此这里选取2013年11月14日6∶00～22∶00的离港数据进行仿真分析.数据集中，推出申请总数M=498架，平均服务时间μ=1.7 min，停机位等待时间阈值G=30 min，根据数据获取年份的航空燃油价格计算得每架飞机滑行燃油消耗成本c=120 元/kg，停机位等待惩罚系数θ=0.245.经过对离港过程仿真，得到高低峰时间段划分如图3所示.

图3中，不同线型代表不同d值时的高低峰期划分，对于所有情形，线段处于横轴时代表此区间为低峰期，处于横轴以外则为高峰期，例如当d=8时，低峰期时间段为6∶00～6∶30、9∶30～10∶00、23∶00～21∶30，其余时段为高峰时段.随着d值的增加，高峰期时段不断减少，其中d=[8,17]所对应的区间数分别为[6,8,8,9,13,13,13,13,13,11].

分别对d=[8,17]时各情形采用动态推出规则对离港过程进行仿真，得到各情形对应的最优成本变化曲线及平均停机位等待时间、平均滑行道等待时间曲线如图4、图5所示.

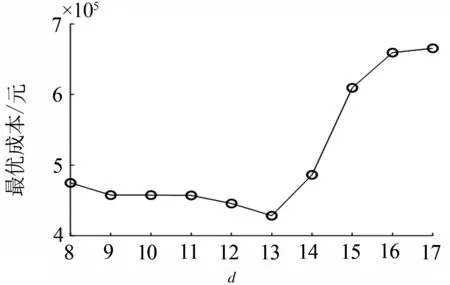
图4 最优成本变化曲线

图5 平均停机位等待时间、平均滑行道等待时间变化曲线

由图4、图5可以看到各种时段划分情况时的成本、平均停机位等待时间、平均滑行道等待时间变化趋势，其中当d=13时成本最优，为428 459.8元.分别对无控制、N-control方法、PDPC方法以及提出的DPDPC方法对离港过程进行仿真，得到各推出控制方法结果如表1所示.

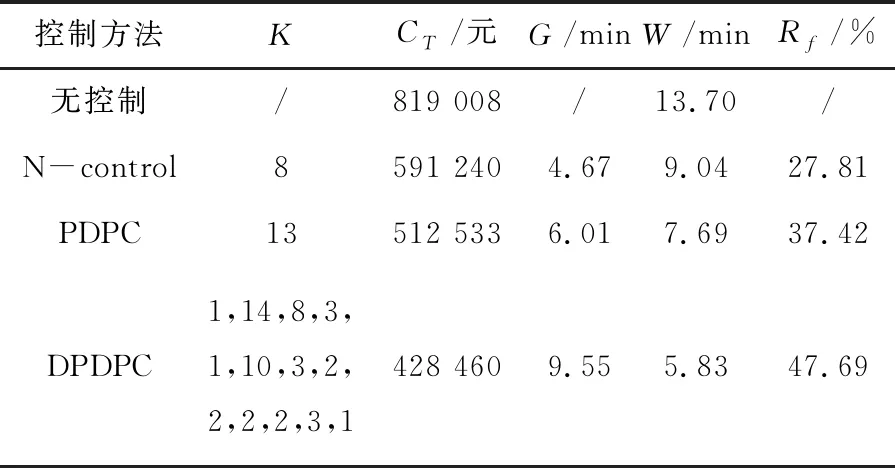
表1 各推出控制方法结果

表1中，Rf为成本减少百分比，从表中可见，相对于无控制、N-control以及常规PDPC控制方法，DPDPC具有更小的离港成本，而各区间所对应的K值为[1,14,8,3,1,10,3,2,2,2,2,3,1]，相对于无控制状态，DPDPC可以减少47.69%的成本，而相对于PDPC方法，成本减少百分比为16.40%.这说明对离港过程进行区间划分的精细化管理有利于节约离港成本.图6描绘了各种控制方法总成本中的燃油成本和惩罚成本的组成.

图6 各推出控制方法燃油成本和惩罚成本组成图

由图6也可看出，DPDPC方法具有最小的成本值，而观察燃油成本和惩罚成本的变化趋势，发现自无控制、N-control、PDPC至DPDPC控制方法，惩罚成本值依次增加，说明其停机位等待的控制力度在不断增加，随之滑行道等待时间则不断减少因此燃油成本在逐渐降低.然而在对各种情况的仿真结果发现，继续加大控制力度(即增加停机位等待时间)并不能帮助模型得到更优的结果.对于时段划分，当d值较小时，时段的划分也较少，这样会增加区间的长度，而区间长度的增加就会减少离港交通量的区分度，使其控制效果及结果向未进行交通量区间划分的情况进行靠拢；而当d值增大使得时段划分较密集时，由于相邻时段的K值不同，尤其当后序时段K值较小时，为了疏散前序时段在滑行道上累积的飞机，后序时段可能会迫使更多的飞机在停机位等待，导致惩罚成本的增加.

以相同的策略对2013年11月15日6∶00～22∶00共计490架飞机的离港数据进行仿真，以验证提出的方法对不同日期的控制效果进行验证，得到结果如表2所示.

表2 验证数据集推出控制方法仿真结果

由验证数据集仿真结果可见，DPDPC控制最高可减少45.98%的运行成本，可为机场管理者提供高效地推出控制方法.

3 结论

在现有的动态推出控制策略基础上，提出了并构建基于离港航班密度划分的动态推出控制模型，针对当前离港服务率设计了离港高低峰期时段划分方法，为了进行模型寻优，提出了一种基于航班时段划分和蒙特卡洛法的动态推出过程求解算法.经过对实际数据进行离港过程仿真求解，得到如下结论：

(1)随着时段划分参数d的增加，平均停机位停留时间呈单调递增趋势，平均滑行道等待时间呈单调递减趋势，然而离港成本呈先减后增趋势，最优成本在d=13时取得；

(2)对比各种推出控制方法，DPDPC具有最优成本，说明对离港过程进行区间划分的精细化管理有利于节约离港成本；

(3)自无控制、N-control、PDPC至DPDPC控制方法，惩罚成本值依次增加，燃油成本在逐渐降低，而燃油成本降低的幅度大于惩罚成本增加的幅度，致使总成本降低；

(4)由于为了方便各推出控制方法的对比，本文采用恒定服务率对区间进行划分，与实际离港情况会有出入，因此下一步研究会对区分不同机型的时段划分进行深入研究.