一类非线性四阶偏微分方程的精确解研究

赵欣，李秀梅，汪颖 ，张继红，梁波

(大连交通大学 理学院，辽宁 大连 116028) *

非线性偏微分方程的精确解研究在实际中十分重要.研究方法上包括李群对称分析方法、级数展开法等.文献[1-2]利用Backlund变换并结合李对称分析方法和幂级数展开法对一类非线性偏微分方程给出了精确解分析.文献[3-4]则研究了一类非线性四阶偏微分方程的精确解.文献[5]对一类非线性四阶偏微分方程求出数值结果.本文是结合经典方法，对四阶非线性偏微分方程进行计算和研究得出求精确解的一种方法.

本文研究一类非线性四阶偏微分方程：

(1)

的精确解，其中k,λ,μ,c,f,g,h均为常数.

1 精确解分析

1.1 方程处理

令u(x,t)=φ(x,t)+R,代入到式(1)中有

(2)

对式(2)进行约化有

(3)

令Φ=φ-φx，为了使式(3)中的每一项依赖于Φ或Φ的微分，要求其系数满足条件：

解得

于是式(3)转化为

(4)

1.2 求解过程

这里考虑两种情况：

情况一：当λ≠0时,考虑方程Φ=0，即

φ-φx=0.

基本解组为φ(x,t)=A(t)ex

其中A(t)是任意函数.

情况二：当λ=0,k≠0时，则式(4)化为

-kΦxx-Φtt+kΦxxx=0

(5)

此时介绍三种研究方案：

方案一：若

Φ=φ-φx,φ-φx=cx+dt

其中c,d为任意常数.可求得基本解组为

φ(x,t)=A(t)ex+cx+dt

其中，A(t)是任意函数.

方案二：若

Φ=φ-φx，φ-φx=x2-kt2,

故基本解组为：

φ(x,t)=A(t)ex+x2-kt2,

其中A(t)是任意函数.

方案三：若Φ=φ-φx，

φ-φx=x3-3k(x-1)t2

基本解组为

φ(x,t)=A(t)ex+x3-3k(x-1)t2

其中A(t)是任意函数.

1.3 推广

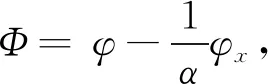
(6)

对式(6)求解得

故式(3)转化为

(7)

此时考虑两种情况.

情况一：λ≠0,考虑方程Φ=0.求得基础解组为

φ(x,t)=A(t)eαx

其中A(t)是任意函数.

情况二：当λ=0,k≠0时，则式(7)转化为

(8)

此时有如下方案给出精确解.

方案一：若

Φ=φ-φx，φ-φx=cx+dt+e

其中c,d,e为任意常数. 基本解组为

φ(x,t)=A(t)eαx+cx+dt+e

其中A(t)是任意函数.

方案二：若Φ=φ-φx,

其中b,e,c为任意常数. 基本解组为

其中A(t)是任意函数.

由方案一和方案二，可得广义形式

这里假设函数f(x)和g(t)分别关于x和t足够光滑，且f‴(x)=0.若满足条件

kfxx+αgtt=0.

此时基本解组为

φ(x,t)=A(t)eαx+f(x)+g(t)

其中A(t)是任意函数.

方案三：若Φ=φ-φx,

其中a,b,c为任意常数.

它的基本解组为

其中A(t)是任意函数.

方案四：若Φ=φ-φx,

其中a,b,c为任意常数.

它的基本解组为

其中A(t)是任意函数.

由方案三和方案四，可得广义形式：

这里假设函数g(t),f(x)及h(x)足够光滑.

若g″(t)=0，及

或者，若g″(t)=c(c≠0)，只要满足下面条件

基本解组为

φ(x,t)=A(t)eαx+f(x)+h(x)g(t)

其中A(t)是任意函数.

2 一类三阶方程的算法扩展

考虑三阶非线性偏微分方程，形式如下

(9)

其中f关于x至少具有一阶导数，μ,a,b,c,k,r,w均为常数.

令u(x,t)=φ(x,t)+R，将其代入式(9)得：

(10)

将式(10)进行约化得：

(11)

令Φ=φxx+αφx+βφ+f，其中β≠0,α为任意常数. 为使式(11)的每一项均包含Φ或者Φ的n阶导数，则系数须满足关系

故将(11)化为

-βΦt+βφxΦ+βφΦx=kΦ

(12)

此时只需求解方程Φ=0，同时注意到Φ=φxx+αφx+βφ+f=0是二阶常系数非齐次线性微分方程，易得该方程一般形式的解. 为获得式(9)一系列精确解，可进行变形，式(11)的每一项都依赖于Φ或者Φ的n阶微分，那么当φ(x,t)是方程Φ=0的解时，则φ(x,t)是式(12)的解. 实际上，在式(12)中，当φ(x,t)是方程Φ=0的解时，φ(x,t)也是(9)的解. 通过改变常数的值，推广了方程Φ=0的基础解，从而得到了(9)一系列精确解.

3 精确解波形图分析

根据所求得的精确解，绘图时都取λ=1,k=-4,α=1；利用Matlab软件将几个典型的波形图绘制如图1～4所示.

(1)A(t)=sin(t)+cos(t),x∈[-20,20],t∈[-10,10]时，其波形如图1所示.

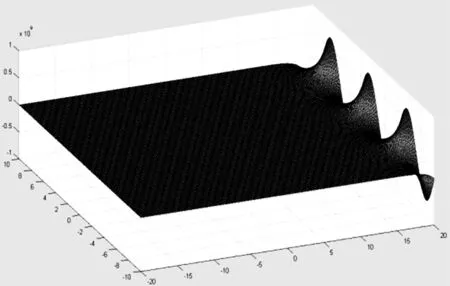
图1 x∈[-20,20],t∈[-10,10]时波形图

(2)A(t)=sin(t)+cos(t),x=-2,t∈[-10,10]时， 其波形如图2所示.

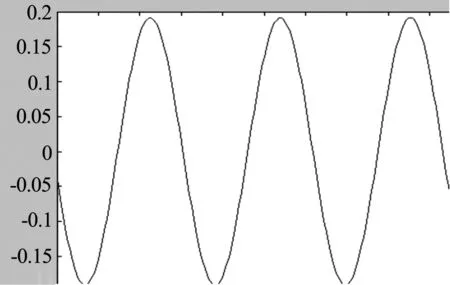
图2 x=-2,t∈[-10,10] 时波形图

(3)A(t)=sh(t),x∈[-1,1],t∈[-50,50]时，其波形如图3所示.

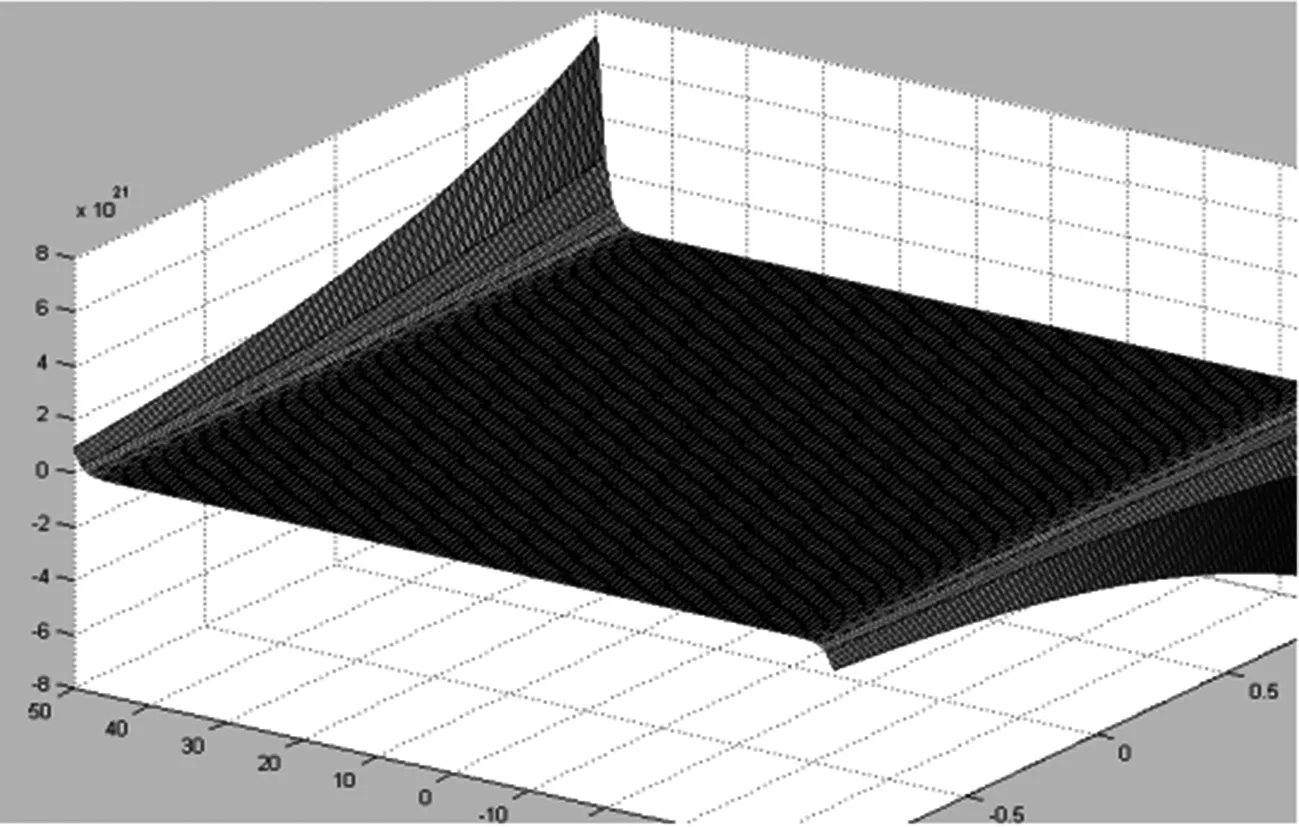
图3 x∈[-1,1],t∈[-50,50]时波形图

(4)A(t)=sh(t),x=-1,t∈[-50,50]时，其波形如图4所示.

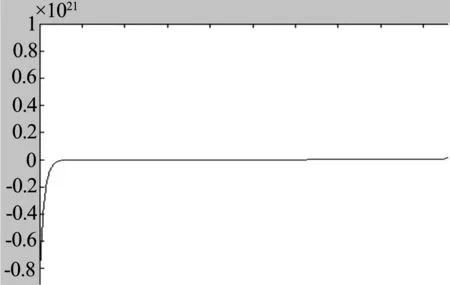
图4 x∈[-1,1],t=50时波形图

4 结论

本文通过将非线性四阶偏微分方程约化为常微分方程的方法，简化了方程结构及复杂的计算，从而获得解的基本形式. 利用参数的变化取得一系列精确解. 遵循四阶方程研究的研究思路，将精确解求法推广到一类三阶非线性偏微分方程上. 最后， 利用Matlab软件绘制出了几个典型情形下

的波形图. 本文的方法为简化求解提供了参考.