基于闭环和前馈控制的高速食品分拣机器人控制技术

柳振宇

薛毓强2

谢祖强3

(1. 福州第二技师学院，福建 福州 350000；2. 福州大学，福建 福州 350000；3. 福建船政交通职业学院，福建 福州 350000)

在食品和药品等轻工业中，通常需要高速完成诸如包装和分拣等操作，其操作对象具有重量轻、体积小等特点[1]。高速并联分拣机器人具有刚度质量比大、无累积误差、移动速度高等优点，被广泛用于食品和制药等轻工业[2]。

目前，有关食品分拣机器人的相关技术研究较多，但对高速并联食品分拣机器人的研究较少。史亚贝[3]提出了一种基于DSP的三自由度分拣机器人控制系统，从硬件和软件两方面构建了一个系统平台。结果表明，在控制系统的驱动控制下，分拣机器人可以准确地从起点移动到终点，轨迹相对平滑，可以达到预期的目标。伍经纹等[4]提出了一种基于ADAMS的三自由度增量机械手运动学分析方法，建立了机械手的数学模型，使用改进的修正梯形加速度曲线来消除运动始末端对机械手的影响。朱向楠等[5]提出了一种基于模糊PID+前馈控制的并联机器人控制方法，并通过仿真验证了其运动位移和角位移误差。结果表明，改进后的控制方法在二自由度并联机器人的运动位移和角位移跟踪误差较小，提高了并联机器人的跟踪精度。张皓宇等[6]对并行机器人的运动控制和NURBS轨迹进行了研究，使用解析方法解决了并行机器人的逆运动学问题，并提出了一种基于多层感知器进行反向传播学习的神经网络实时求解正运动学问题。结果表明，在迭代次数和执行时间较少的情况下，位置和方向参数的精度均为0.01 mm。但是，上述研究尚未对高速并行分拣机器人的控制方法进行详细研究，并且未考虑诸如外部干扰等不确定因素对系统的影响，有一定的局限性，需不断改进和完善。

针对高速并联食品分拣机器人的控制方法，文章拟提出一种将传统运动学闭环控制和力矩前馈控制相结合的高速并联食品分拣机器人的控制方法，在原有遗传算法整定PID控制参数的基础上，引入力矩前馈控制方法进行控制，并进行验证实验，旨在为研究高速并联食品分拣机器人的控制方法提供依据。

1 系统概述

图1为高速并联食品分拣机器人的体系结构，主要由上位机系统和下位机系统两个部分组成[7]。上位机系统是集成到工业计算机平台中的一组软件系统，其主要功能包括可视化、模型求解、视觉处理、数据集成处理以及与下位机的信息交互[8]。下位机系统(即以主控制芯片为核心的嵌入式软件和硬件系统)主要提供控制算法集成、伺服电机闭环控制、实时监控和与上位机的实时数据交互等功能。

图2为高速并联食品分拣机器人的本体，由静平台、动平台、主动臂和从动臂4部分组成[9]。静平台配备有通过法兰连接的伺服电机和减速器，从动臂通过球形铰链连接到动平台，每个分支链包含一个主动臂和一个从动臂，动平台由主、辅平台组成[10]。

2 建模与控制方法

高速并行分拣机器人机械部分建模分为运动学和动力学两个部分[11]。运动学分析，尤其是逆解分析，是对分拣机器人进行控制的基础。动态分析是求解关节力矩和实现动态控制的基础。

2.1 运动学模型

分拣机器人的动平台只进行平移运动，且各支链从动臂的运动相同，因此可以将研究转化为分拣机器人结构简图(见图3)。

在静平台中心建立参考坐标系O-xyz，将动平台看成质点P1和P2，则主(辅)动平台参考点P1(P2)的位置矢量r=(xyz)T如式(1)所示[12]。

(1)

式中：

ei——从O到Ai的向量；

l1——主动臂杆长，mm；

ui——单位矢量(沿主动臂)；

l2——从动臂杆长，mm；

wi——单位矢量(沿从动臂)；

s——P1到P2的距离,mm;

根据机构的装配模式，主动臂的转角θi整理如式(2)所示[13]。

(2)

式中：

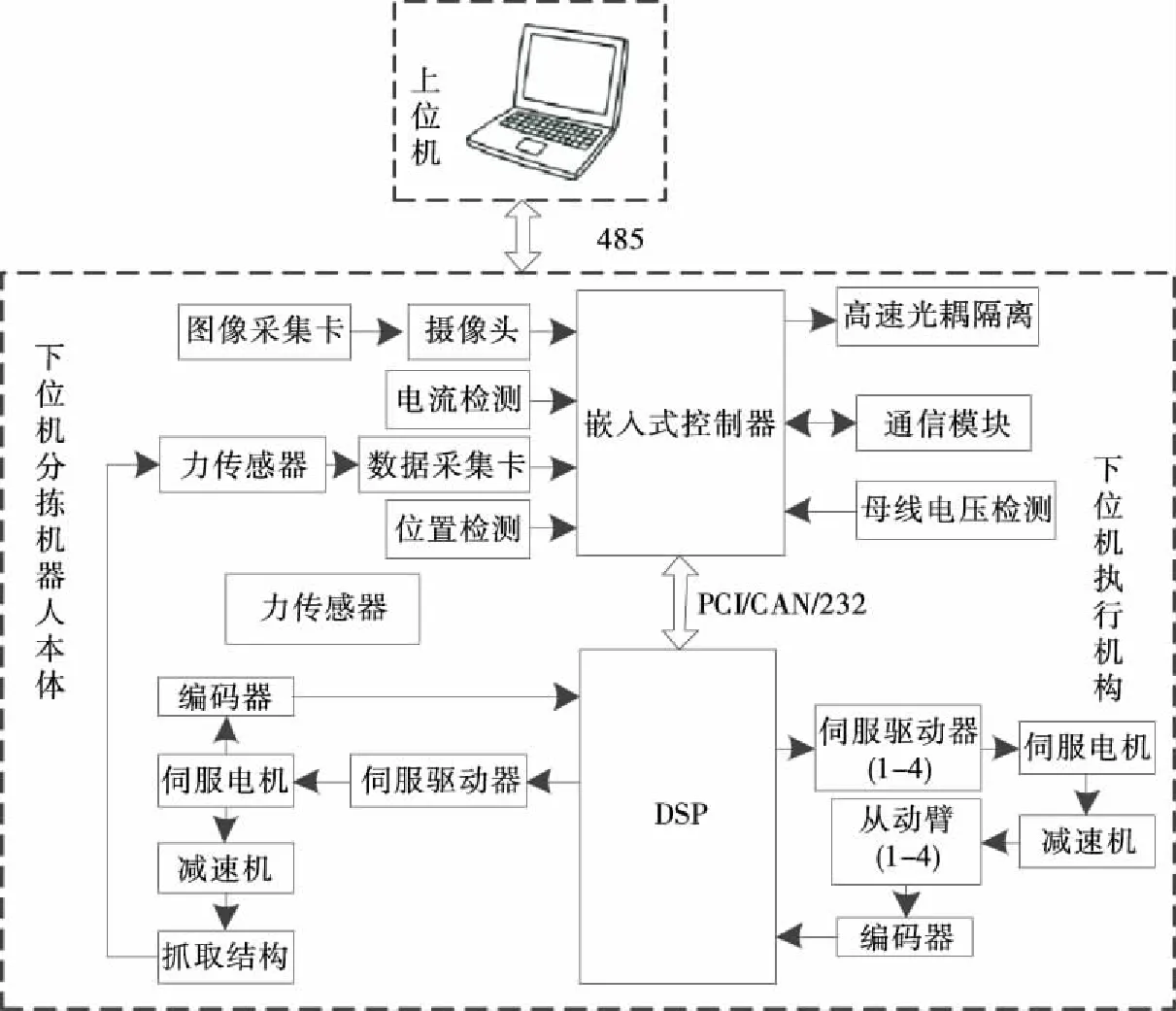
图1 系统结构

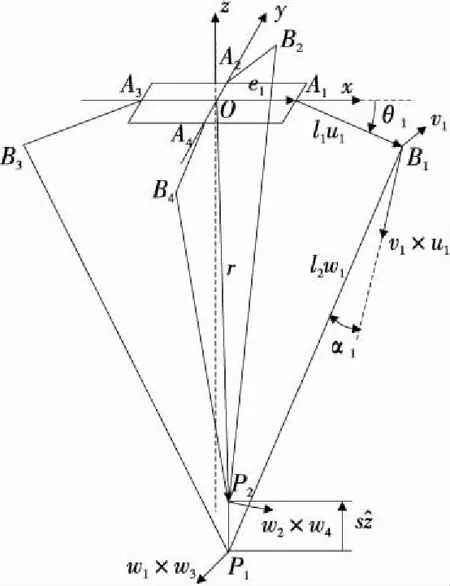
图3 分拣机器人结构简图

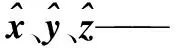
根据式(2)求解θi后，wi的值如式(3)所示[14]：

(3)

将式(1) 关于时间求一次导数得到速度模型如式(4)所示[15]。

Jqθg=Jxxg，

(4)

式中：

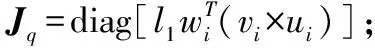
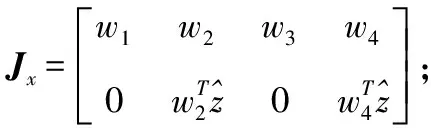
J——雅克比矩阵。

将式(1)关于时间求二次导数得到角加速度模型如式(5)所示[16]。

θgg=Jxgg+f(xg)，

(5)

式中：

f=(f1f2f3f4)T；

2.2 动力学模型

在完成刚体动力学建模前，应将整个食品分拣机器人视为刚性的，忽略分拣机器人的摩擦，并且应将分拣机器人的主臂和从属臂视为匀质杆件[17]。

参考食品分拣机器人的结构图(图3)，在第i个支链的从动臂链接上建立坐标系Obi-xbiybizbi，其中，原点Obi在分拣机器人的每个支链的质心上，zbi轴的正方向是连杆轴线的方向，垂直于xbi轴，且在wi与wi×ui平面中，根据右手定则确定ybi轴方向。并依据虚功原理，如式(6)所示[18]。

(6)

式中：

τ——主动关节驱动转矩，τ=(τ1τ2τ3τ4)T；

rgg——动平台质心加速度，rgg=(xggyggzgg)T；

m1、m2——主平台和辅平台质量，kg；

IA——主动臂折算到转轴的转动惯量，kg·m2；

τAg——主动臂关于转轴的重力矩，N·m；

Grod——从动臂连杆的重力，N；

Arod——从动臂连杆的惯性力，N；

Mrod——从动臂连杆的惯性力矩，N·m。

将虚位移δθ=Jδr代入式(6)，可得食品分拣机器人刚体动力学模型如式(7)所示。

τ=τA+τp+τrod，

(7)

式中：

τA、τrod、τp——作用在主动臂、从动臂、动平台与负载上的力与力矩；

τA=IAθgg+τAg；

τp=J-T(margg+mgg)。

2.3 控制方法

确保高速并联食品分拣机器人准确运行的最基本方法是制定控制方法，控制中需要解决的是建模和参数的不确定性[19]。建模不确定性无法排除，只能不断提高控制器的鲁棒性，而参数的不确定性可以通过自整定来克服。

为了提高高速并联分拣机器人分拣的快速性和抗干扰能力，提出一种基于遗传算法自整定的PID+前馈运动控制方法，即在原有遗传算法整定PID控制参数的基础上，引入力矩前馈控制方法进行动态控制，与反馈控制一起作用至电机轴上[20]。

通过遗传算法对食品分拣机器人的PID参数进行整定时，有必要建立评价指标，以确保调整过程的合理性和准确性。文中，时间与绝对误差乘积的积分作为评价指标，即：

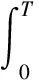
(8)

表1为遗传算法进行整定后，速度环和位置环PID参数的最优解。

高速并联食品分拣机器人的实际操作状态通常是高速且频繁的加/减速，会导致多支链相互作用和惯性力(如科氏力、向心力)的干扰越大，传统的PID控制无法满足系统的快速响应[22]。因此，在传统运动学闭环控制的基础上，引入力矩前馈控制方法进行补偿，抵消分支链耦合和动态力对系统控制的部分影响。

运动学闭环控制系统虽然具有一定的抗干扰功能，但无法保证高速分拣机器人控制系统的准确性，引入力矩前馈控制方法后，系统可以实时求解变量的动态模型，获得期望力矩并执行力矩前馈补偿。由于电流环采取封装形式，通常不对用户开放。因此，力矩前馈补偿的作用点基本会在电流环路之前。相对而言，力矩前馈具有系统性和互补性优势，能有效改善系统动态性能。建模误差和摩擦的影响由可闭环控制消除。图4为力矩前馈控制框图。

表1 最优参数

其原理是：使用先前建立的动力学模型来计算操作期间分拣机器人的位置和方向的变化，以获得此时的期望力矩。通过分拣机器人的单链力矩前馈控制器，所需力矩被转换为电信号，该信号作用在电流回路上，以实时抑制高速动态干扰。通常情况下，分拣机器人的运动轨迹是相对固定的，可以使分拣机器人的各种状态进行离线求解，并通过查表来获得驱动扭矩，从而大大减少在线操作量。力矩前馈控制环节的传递函数GTF为：

(9)

3 结果与分析

3.1 试验参数

为了对所提出的控制方法进行验证，将所提出的控制方法与常规PID控制方法和常规PID+前馈控制方法进行比较。为了确保试验结果的准确性，通过多次测量取平均值。表2为试验环境，使用型号为B7104Q3H7GKM00T5的LAFERT电机，Intel i5处理器计算机，内存8 G，win10系统，控制平台由运动控制软件TwinCAT构建。

3.2 不同控制方法对比分析

将文中控制方法与传统的PID控制方法以及传统的PID+前馈控制方法进行比较。通过从站的伺服驱动器获得分拣机器人电机编码器的关节位置，比较分拣机器人的4个关节的指令位置与实际位置，并对差值进行数据处理。图5为分拣机器人采用不同控制方法的4个驱动关节的位置跟踪误差，不同控制方法下各轴位置跟随误差的绝对值最大值和平均值见表3。

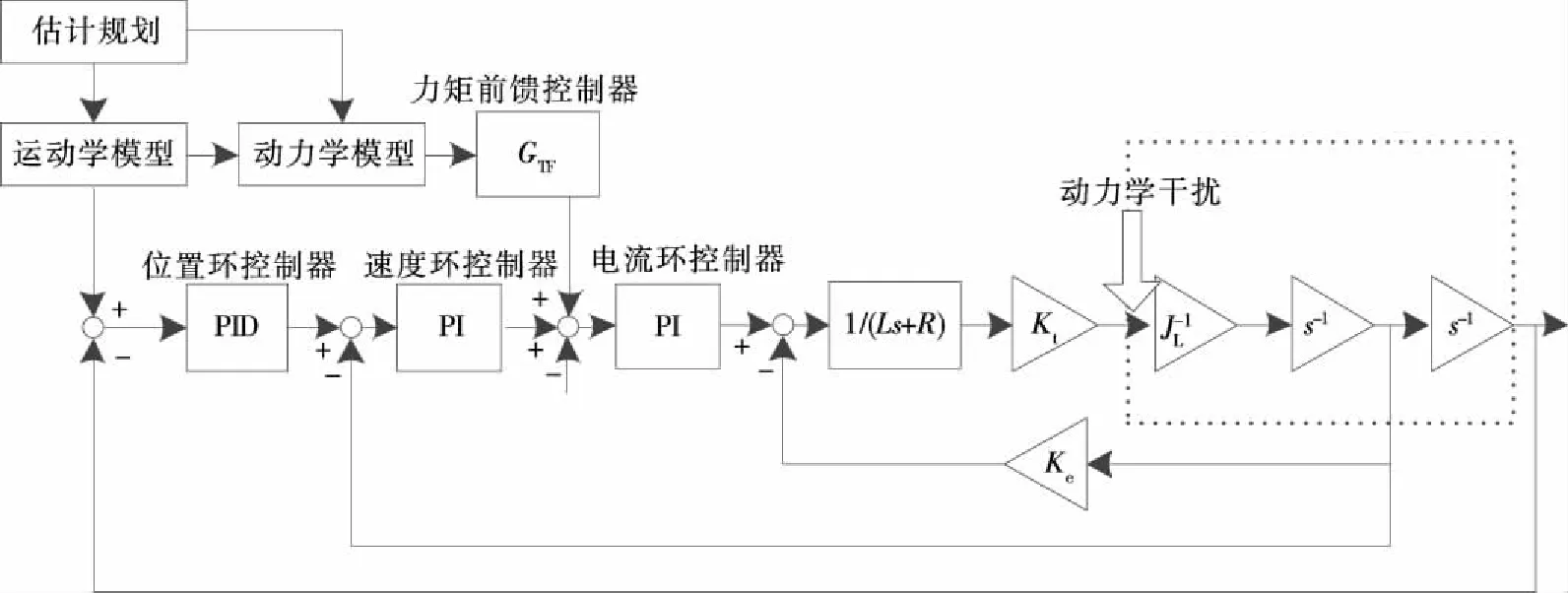
图4 力矩前馈控制模型

表2 试验参数

由图5和表3可知，相比于传统的PID控制方法，加入前馈控制方法后可将最大和平均关节位置跟踪误差降低超过35%。加入自整定和前馈控制的方法最大和平均位置跟踪误差降低超过65%，极大地提高了各关节的跟踪能力，从而实现了分拣机器人的高精度控制。图6为3种控制方法下分拣机器人末端执行器在工作空间中的轨迹误差比较，由关节位置正向运动学正解得到。

图5 不同控制方法的空间跟随误差对比

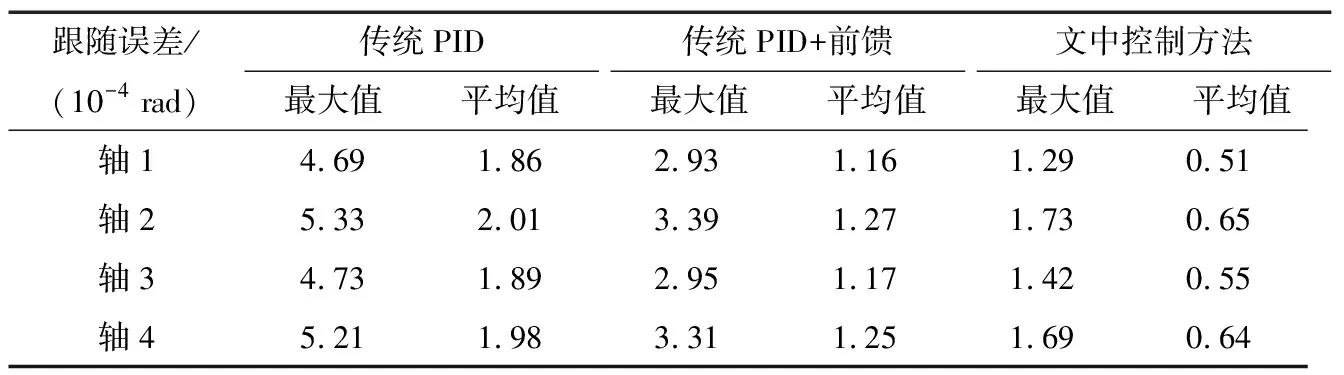
表3 不同控制方法位置跟随误差最大值和平均值

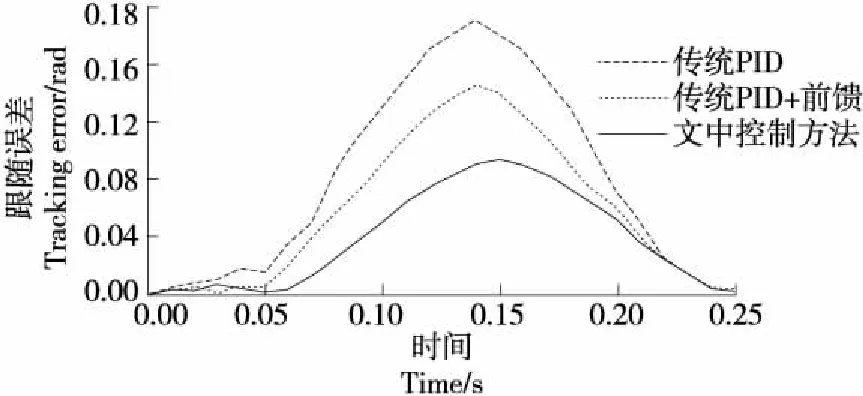
图6 不同控制方法轨迹误差对比

由图6可知，传统PID控制方法最大轨迹误差为0.192 mm，使用传统的PID+前馈控制方法的最大轨迹误差为0.143 mm，降低了25.52%；使用遗传算法优化的PID+前馈控制方法的最大轨迹误差为0.094 mm，降低了51.04%。

综上，通过前馈控制可以提高系统控制精度，但无法解决系统模型误差，因此通过自适应整定可以进一步提高控制精度，而遗传规则正好满足此要求。通过动态前馈补偿和遗传优化的PID反馈调节相结合可以有效提高系统的控制精度。为了进一步验证文中控制方法的有效性，对控制关节的实测转矩和理论转矩进行进一步比较，结果如图7所示。

由图7可知，实测力矩曲线与理论值曲线非常接近，且峰值与趋势基本相同，证实了文中控制方法的有效性。对误差产生的原因进行分析，可能是由模型参数误差、环境噪音等引起的。

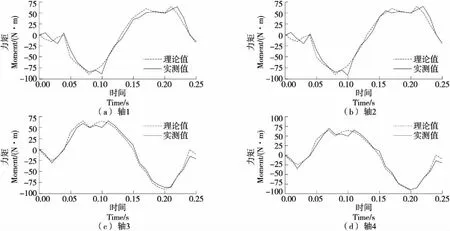
图7 关节实测力矩与理论值对比

4 结论

提出了一种将传统的闭环运动学控制和力矩前馈控制相结合的高速并联食品分拣机器人控制方法。在原有遗传算法整定PID控制参数的基础上，通过力矩前馈控制方法进行动态控制。结果表明，与传统的PID控制相比，关节位置跟踪最大和平均误差降低超过65%，最大轨迹误差降低超过50%，极大地提高了高速并联食品分拣机器人各关节的跟踪能力，实现了各关节的高精度控制。高速并联食品分拣机器人的控制方法仍处于试验阶段，文中仅对跟踪精度和关节转矩进行比较和分析，未对加速度变化和负载变化进行研究，后续将注重提高控制系统性能，完善高速并联食品分拣机器人系统。