Discussion on“Analysis of Bingham fluid radial flow in smooth fractures”[J Rock Mech Geotech Eng 12 (2020) 1112-1118]
Vn Thnh Hong, Wnkun Liu, Jng Min Prk,*
a School of Mechanical Engineering, Yeungnam University, Daehak-ro 280, Gyeongsan, 38541, Republic of Korea
b Department of Mechanical Engineering, The University of Danang - University of Science and Technology, Nguyen Luong Bang Street 54, Danang, Viet Nam
Keywords:Rock grouting Radial flow Bingham fluid Analytical solution
ABSTRACT Recently,Zou et al.(2020a)published a theoretical analysis on the radial flow of a Bingham fluid,where they argued that the classical analysis by Dai and Bird(1981)violates the mass conservation.The present discussion aims to clarify this conflict between those two studies. It is noted that Zou et al. (2020a)presumed the gap-wise mass flux is negligible in the mass conservation equation, while Dai and Bird(1981)did not require so in their model,and this is found to be the origin of the conflict.In fact,Dai and Bird (1981)’s model is shown to not violate the mass conservation. Therefore, those two models should be viewed as separate models derived from different perspectives. Details of the major difference between the two models are discussed.
1. Introduction
Cement grouting is frequently encountered in rock engineering(Zou et al.,2020a,b).The cement grouting involves the flow of non-Newtonian fluid, and the Bingham model has been widely employed for the flow analysis of cement grouting.
In many cases of cement grouting,the flow field can be modeled as an axisymmetric radial diverging flow between parallel disks(Gustafson et al., 2013). The theoretical analysis of the axisymmetric radial flow of a Bingham fluid was first carried out by Dai and Bird (1981). They extended the existing analytical solution of the plane slit flow to the radial flow in order to derive an equation relating the volume flow rate and the pressure gradient. The analytical solution for this model was later obtained by Bird et al.(1983) and Huang et al. (1987). Recently, Zou et al. (2020a) presented another type of analytical solution for the radial flow of a Bingham fluid,where they also presented an excellent review of the previous studies regarding the radial flow of the Bingham fluid.
The present study is motivated by Zou et al. (2020a). As noted,there have been some issues regarding the analytical solution in the radial flow of the Bingham fluid(for instance,see El Tani and Stille(2017)),and Zou et al.(2020a)aimed to clarify the issue from their study. They concluded that the yield surface zpshould be independent of radial position r, otherwise the mass conservation will be violated. In this regard, they argued that the classical analysis by Dai and Bird (1981) fails to satisfy the mass conservation.In this study,we aim to resolve this conflict between Zou et al.(2020a)’s model and the classical model by Dai and Bird(1981).
Fig. 1 introduces the coordinate system and basic dimensions used in the description of the radial flow. It should be mentioned that,in the present study, we will only consider the steady singlephase flow of a Bingham fluid. In other words,the groundwater is not considered,and the fracture is assumed to be completely filled with the Bingham fluid.The half-gap distance is denoted as h,and the inlet and the outlet are located at r = r1and r = r2, respectively. The domain is characterized by ε = h/r2≪1. Due to the symmetry with respect to the mid-plane z = 0, we will consider only the upper half of the domain.

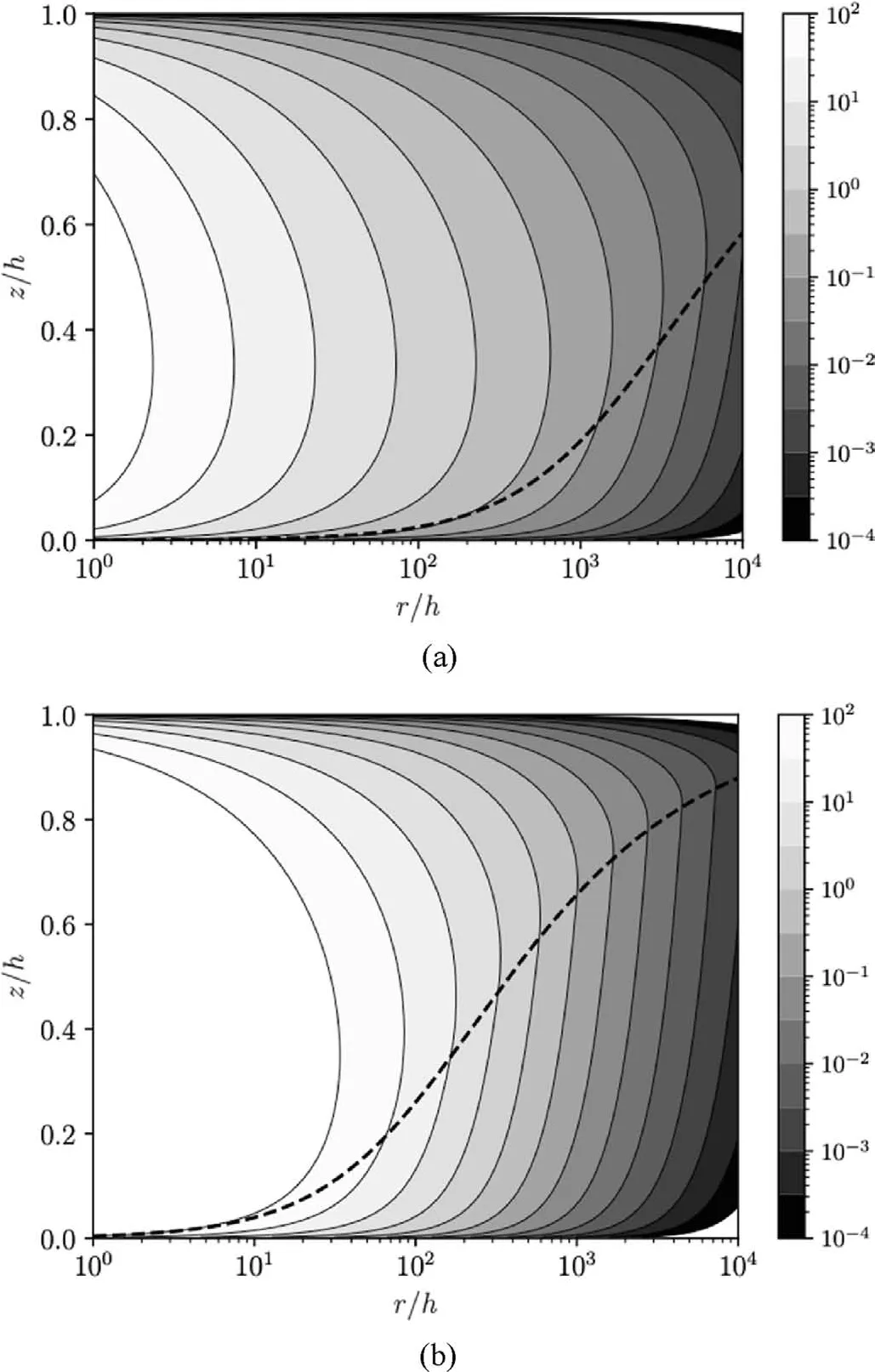
Fig. 2. Contour plots of normalized radial velocity ur/U predicted by Dai and Bird(1981)’s model (a) and Zou et al. (2020a)’s model (b) when Bn = 0.0625. The dashed curve represents the yield surface (z = zp).
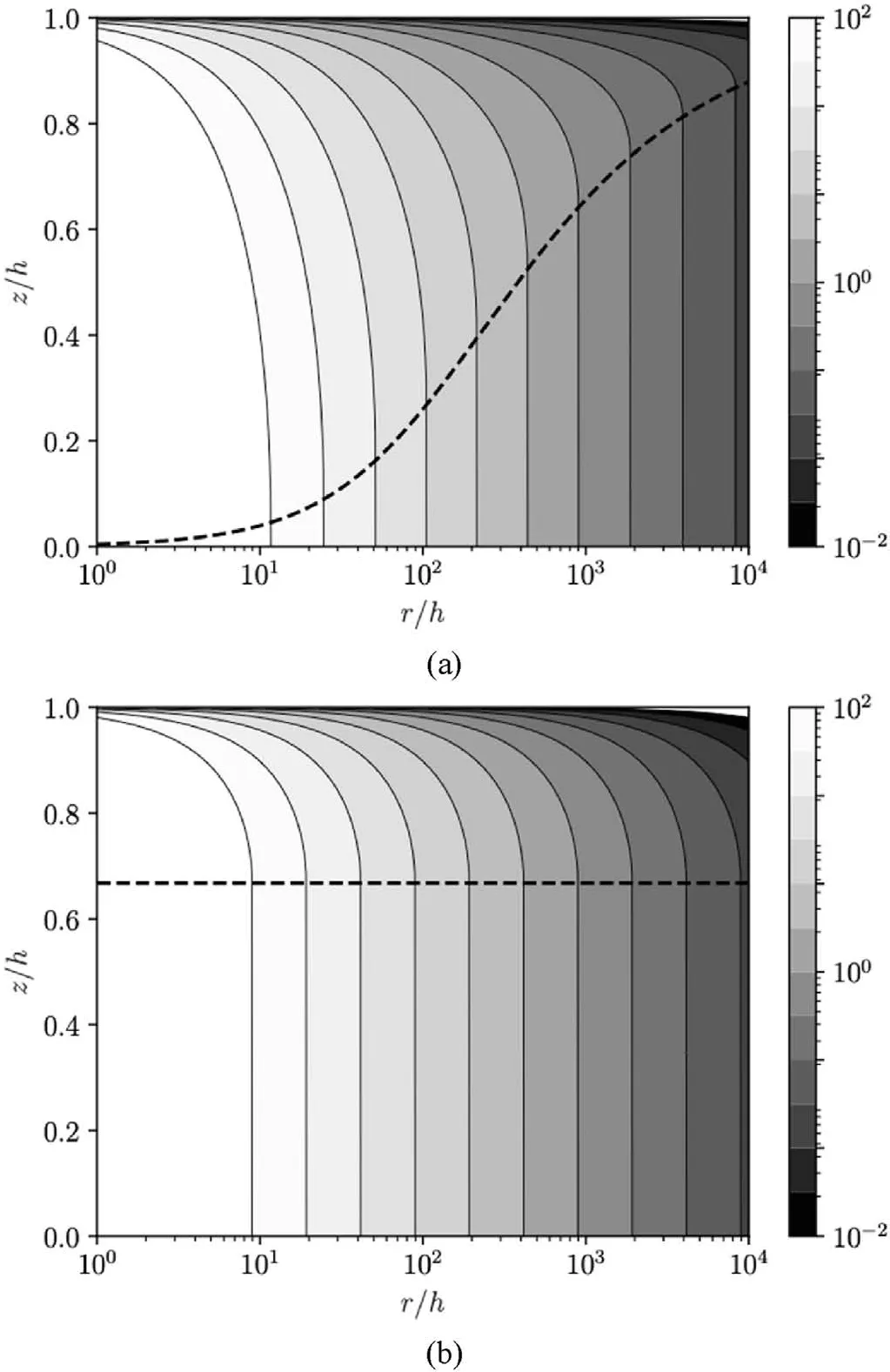
Fig. 3. Contour plots of normalized radial velocity ur/U predicted by Dai and Bird(1981)’s model (a) and Zou et al. (2020a)’s model (b) when Bn = 0.1. The dashed curve represents the yield surface (z = zp).
Since ε ≪1, we can use the lubrication approximation, and details of the governing equation and boundary condition will be described in Section 2.At this moment,it should be mentioned that there are some critical differences between Zou et al. (2020a)’s model and Dai and Bird (1981)’s model, which will be also emphasized in Section 2. In Section 3, the two models are summarized. In Section 4, the two models are compared in terms of the flow field and the pressure loss. Section 5 summarizes the results and further considerations are discussed.
Meanwhile, in the radial flow with the lubrication approximation, the constitutive equation for a Bingham fluid reads as(Lipscomb and Denn,1984; Zou et al., 2020a):

Fig.1. Coordinate system and basic dimensions for radial flow.

where τrzis the shear stress, τ0is the yield stress, uris the radial component of the velocity vector, and η1is the plastic viscosity.
2. Dai and Bird (1981)’s model revisited
By noting the similarity with the plane slit flow, Dai and Bird(1981) derived an equation for the volume flow rate (Q) for the radial flow which reads as

where p is the pressure.
In the original paper by Dai and Bird (1981), only an approximate solution for ∂p/∂r could be obtained. Later, the analytical solution was presented by Bird et al.(1983)and Huang et al.(1987),which reads as

An explicit expression for the pressure p(r)was also obtained by Huang et al. (1987) which will be introduced in the next section.
In this section,we will show that the volume flow rate equation by Dai and Bird (1981) can be also obtained from the mass and momentum conservation equations with appropriate boundary conditions, which proves that Dai and Bird (1981)’s analysis does not violate the mass conservation. The derivation procedure is similar to one presented for the squeeze flow of a Bingham fluid by Muravleva (2017), while the boundary condition at the wall is different. Meanwhile, we will emphasize the fundamental difference between Zou et al. (2020a)’s analysis and the present formulation.
According to the lubrication approximation, the conservation equations of mass and momentum for steady incompressible axisymmetric flow can be written as (Bird et al.,1987; Muravleva,2017):

where uzis the axial component of the velocity vector.At this point,it is important to note that Zou et al.(2020a)neglected the gap-wise mass flux,i.e.∂uz/∂z term,in the mass conservation equation,while we do not make such an assumption a priori in this study.We will discuss in Section 5 why ∂uz/∂z term is not negligible in the mass conservation equation.
The mass conservation equation can be integrated with respect to z-direction as follows:

where we have applied no-slip boundary condition at wall(z = h)and symmetric condition at mid-plane (z = 0). By multiplying with r and integrating with respect to r, the last line in the above equation can be written as

which can be rewritten as

From now on, let us derive explicit expressions for the yield surface zpfrom the momentum conservation equation. From Eq.(7),one can find that p = p(r).By integrating Eq.(6)with respect to z, one can find

Due to the symmetry with respect to the mid-plane, we can apply τrz|z=0= 0, and therefore we have

It is important at this point to note that Zou et al.(2020a)did not apply τrz|z=0= 0, but they applied τrz|z=zp= τ0.
The magnitude of the shear stress should be equal to the yield stress τ0at the yield surface (z = zp), which can be written as

Therefore, the yield surface is given as

In this study,we only consider radial diverging flow where ∂p/∂r <0, and therefore we have

Therefore, one can find that the yield surface zpdepends on r.On the other hand,it is important at this point to note that the yield surface zpby Zou et al. (2020a) is independent of r.
From now on, let us derive explicit expressions for the velocity urand uz. In the yielded region (zp≤z ≤h), the constitutive equation can be written as

In the present study, we only consider the upper half of the domain where ∂ur/∂z ≤0. Therefore, the above equation can be rewritten as

One can substitute Eq.(12)and integrate with respect to z from h to z, which results in
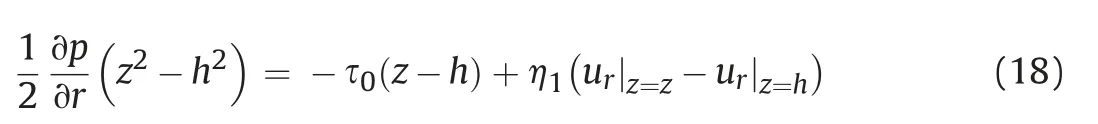
Applying no-slip boundary condition at z = h and rearranging the equation result in

To find uzin the yielded region, one can integrate Eq. (5) with respect to z from h to z as follows:

By using Eq. (19) and applying no-slip boundary condition at z = h, one can find

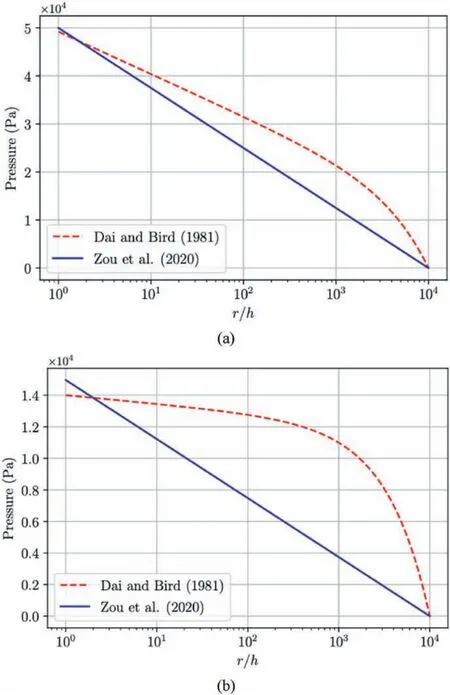
In the unyielded region(0 ≤z To find uzin the unyielded region,one can integrate Eq.(5)with respect to z from 0 to z as By noting that ur= ur(r)in the unyielded region and applying symmetry condition at z = 0, one can find uzin the unyielded region as By substituting Eqs. (19) and (22) into Eq. (10), and after some manipulations, one can find By applying zp= - τ0(∂p/∂r)-1, the above equation can be rewritten as which is exactly the same as Eq. (3). It is shown here that the classical model by Dai and Bird (1981) can be obtained from the conservation equations of mass and momentum. Therefore, it is shown explicitly that Dai and Bird(1981)’s model does not violate the mass conservation. Let us summarize Dai and Bird (1981)’s model and Zou et al.(2020a)’s model in this section. Then we will present a comparison between the two models in terms of the flow field and the pressure loss in Section 4. Meanwhile, it can be noted that the volume flow rate equation for both Dai and Bird(1981)’s model and Zou et al. (2020a)’s model can be written in common as where ∂p/∂r and zpdepend on the model. (1) Yield surface It should benotedthatzp→0 asr→0,while zp→h asr→+∞,and zpis increasing with r. (2) Pressure gradient (3) Pressure where r0is the radial location at which p(r0)is given as a boundary condition. See Appendix A for details of the derivation procedure.This equation can give information regarding the relationship between the pressure loss and the flow rate Q.It should be noted that zpdepends on Q. (4) Velocity where The above equation for ∂zp/∂r can be obtained by differentiating Eq. (25) with respect to r followed by some manipulations. One should note that Zou et al. (2020a) assumed the flow is unidirectional, i.e. uz= 0, which makes their model be much simpler than Dai and Bird (1981)’s model. This assumption was not explicitly stated by Zou et al. (2020a), but it can be deduced from the fact that ∂uz/∂z is neglected in the mass conservation equation. (1) Yield surface where p1and p2are the pressures at r = r1and r = r2,respectively. (2) Pressure gradient where (3) Pressure (4) Velocity In this section,we will compare the two models in terms of the velocity field ur(r,z), the pressure distribution p(r), and finally the relationship between the flow rate Q and the pressure loss p(r1)- p(r2). For the first two items,we will consider two cases with different flow rates of Q = 1×10-5m3/s and 1.6×10-5m3/s, so that the flow characteristics of the two models can be compared for different Bingham numbers. The geometrical parameters are fixed as h = 1×10-3m, r1= 1×10-3m, and r2= 10 m, while the pressure at r2is fixed as p2= 0 Pa.Meanwhile,the Bingham fluid has the plastic viscosity of η1= 1 Pa s and the yield stress of τ0= 1 Pa. The characteristic velocity in r-direction can be defined as and Bingham number is defined as Figs.2 and 3 show the normalized radial velocity(ur/U)and the yield surface when Bn = 0.0625 and 0.1, respectively. As far as the prediction of the yield surface is concerned, the two models are very distinct.As mentioned before,zpdepends on r in Dai and Bird(1981)’s model,while Zou et al.(2020a)’s model predicts a constant yield surface.In Dai and Bird(1981)’s model,the yield surface and the velocity field particularly near the inlet (r = r1) are not much affected by Bn.On the other hand,in Zou et al.(2020a)’s model,the overall velocity field is affected by Bn since the yield surface is increased uniformly as Bn increases.Fig.4 shows the profile of the radial velocity when Bn = 0.1. The difference between the two models in terms of the velocity is shown clearly in this figure.As Bn decreases, however, two models will become almost identical because the fluid behaves like a Newtonian fluid if Bn ≪1. Fig. 5 shows the pressure distribution for two cases of Bn=0.0625 and 0.1.In general,Dai and Bird(1981)’s model predicts higher pressure than Zou et al. (2020a)’s model in most part of the domain except near the inlet, and the pressure distribution is very distinct between the two models. However, it is interesting to note that the difference between the two models particularly at the inlet(r = r1) is not so notable. One can also observe that the pressure predictions by the two models become closer as Bn decreases. Fig. 6 shows the relationship between the flow rate Q and the pressurelossp(r1)-p(r2).Bothmodelspredictalmostthesamevalue of the minimum pressure loss required to generate a flow. Dai and Bird (1981)’s model predicts slightly lower pressure loss than Zou et al. (2020a)’s model, but the difference is not significant in general.Therefore,asfarastherelationshipbetweentheflowrateandthe pressure loss is concerned,the two models offer a similar result. Fig. 7 shows the normalized axial velocity (uz/W) by Dai and Bird (1981)’s model, where the characteristic velocity in z-direction is defined as with ε = h/r2.It is noted that uz≥0 in the overall domain,and the axial velocity is found to be more pronounced near the inlet r = r1.It is interesting to note that the maximum axial velocity always appears slightly above the yield surface.As mentioned before,Zou et al. (2020a)’s model assumes uz= 0 which is one of the major differences compared to Dai and Bird(1981)’s model. As one can note from Eq. (43), the axial velocity is nearly negligible compared to the radial velocity as ε→0. This is clearly observable in Fig. 8 where both the axial and radial velocity components are normalized by the same characteristic velocity U, and therefore, the axial velocity is shown to be nearly negligible.However,it should be mentioned that the axial contribution in the mass conservation equation,i.e.∂uz/∂z term in Eq.(5),might not be negligible in general, and we will discuss this in more detail in Section 5. Fig. 5. Pressure distribution for Bn = 0.0625 (a) and 0.1 (b). Fig. 6. The flow rate as a function of the pressure loss between inlet and outlet. (a)shows a magnified view near the origin of (b). Fig. 7. Contour plots of normalized axial velocity uz/W predicted by Dai and Bird(1981)’s model when Bn = 0.0625 (a) and 0.1 (b). The dashed curve represents the yield surface (z = zp). Fig.4. Profiles of normalized radial velocity ur/U at two radial locations of r/h = 1×104 (a) and 10 (b) when Bn = 0.1. We present a theoretical study on the radial diverging flow of a Bingham fluid. This study clarifies the conflict between the recent study by Zou et al. (2020a) and the classical study by Dai and Bird(1981).The fundamental difference between the two models can be summarized as follows: (1) Zou et al. (2020a) assumed that the gap-wise mass flux is negligible in the mass conservation equation, while Dai and Bird(1981) did not explicitly state so. (2) As for a boundary condition for the shear stress, τrz= 0 is applied on z = 0 to arrive at Dai and Bird (1981)’s model,while Zou et al. (2020a) applied |τrz| = τ0on z = zp. As a result,in Zou et al.(2020a)’s model,τrzis not fully defined in the unyielded region (0 ≤z (3) For Dai and Bird(1981)’s model,τrz= τ0is applied on z = zpto define the yield surface zpwhich is found to depend on r.In contrast,Zou et al.(2020a)assumed that zpis independent of r since they assumed uz= 0, and zpcould be obtained from the force balance equation. The argument by Zou et al. (2020a) that Dai and Bird (1981)’s model violates the mass conservation seems to originate from the first item mentioned above.The present study clarifies that Dai and Bird(1981)’s model does not violate the mass conservation,as far as∂uz/∂z term is not neglected in the mass conservation equation. A simple dimensional analysis can be helpful to understand why ∂uz/∂z is not negligible in the mass conservation equation. With the characteristic velocities of U and W defined in Eqs. (41) and (43),respectively, one can find the order of magnitude of each term in the mass conservation equation as follows: Therefore, one cannot simply neglect ∂uz/∂z in the mass conservation equation,since its order of magnitude can be the same as the other terms. In the lubrication approximation, it has been commonly assumed that uzis negligible since uz~W = Uε where ε =h/r2≪1.It had been also acceptable to assume ∂uz/∂z is negligible in many cases of non-Newtonian fluid flow,for instance,see Na and Hansen(1967).However,the present result suggests that particular care might be required regarding this assumption depending on the problem. In the field of cement grouting analysis, it would be acceptable to neglect the gap-wise mass flux because the grout propagation is determined by the radial velocity only. However,in the flow kinematics point of view, ∂uz/∂z might not be negligible,because the gap-wise (z-directional) velocity gradient can be driven by the variation of the yield surface profile along the flow direction (r-direction). Fig.8. Profiles of normalized velocity components ur/U and uz/U at radial location of r/h = 10 when Bn = 0.1. Note that both the radial and axial velocity components are normalized by the radial characteristic velocity U. Because of the fundamental difference mentioned above, the flow field shows a significant difference between Dai and Bird(1981)’s model and Zou et al. (2020a)’s model, which is especially notable at higher Bn. However, when it comes to the relationship between the pressure loss and the flow rate,it is found that the two models are not much distinct.Zou et al.(2020a)also noted that the analysis by Gustafson et al. (2013), where Dai and Bird (1981)’s model is employed, is similar to their analysis in terms of the penetration length and the flow rate. As far as the flow kinematics is concerned,Dai and Bird(1981)’s model would be more desirable than Zou et al. (2020a)’s model,because it does not limit z-directional degree of freedom.However,in the view of practicality especially in the field of rock engineering,Zou et al.(2020a)’s model possesses an advantage over Dai and Bird(1981)’s model, which can be summarized as follows. In Zou et al.(2020a)’s model,the flow is assumed unidirectional,which significantly simplifies the analysis.This is particularly useful when the fluid rheology becomes more complicated. For instance,the simplified approach offers an analytical solution for the radial flow of a yield-power-law fluid (Zou et al., 2020a), which is also found to agree acceptably well with experiments (Shamu et al.,2020). Therefore, it should be noted that Zou et al. (2020a)’s model benefits from its practicality due to the simplicity and reasonable level of accuracy. Finally, we want to mention that the present study considers only the leading order solution of the lubrication approximation(Muravleva 2017). However, one can also build a higher order solution based on the asymptotic expansion by Muravleva (2017)after only some manipulations regarding the boundary condition.The higher order solution so obtained will reveal that the unyielded or plug region in the radial flow actually yield weakly, and this region can be termed as a pseudo-plug region in this regard (Putz et al., 2009). Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Acknowledgments This research was financially supported by Yeungnam University Research Grant Program 2019. Appendix A. Supplementary data Supplementary data to this article can be found online at https://doi.org/10.1016/j.jrmge.2021.03.001.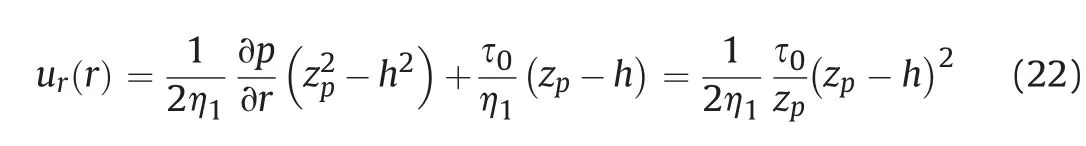
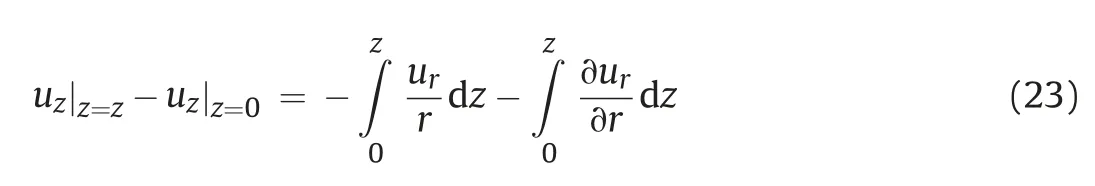

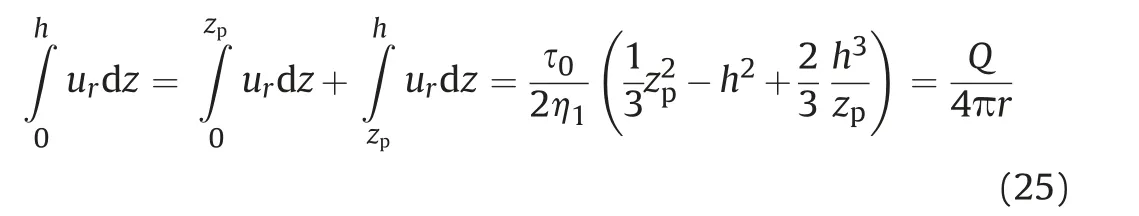

3. Summary of two models

3.1. Dai and Bird (1981)’s model





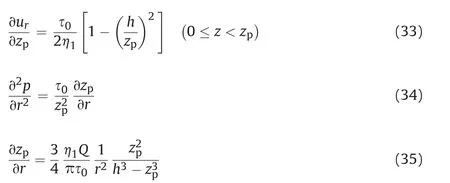
3.2. Zou et al. (2020a)’s model
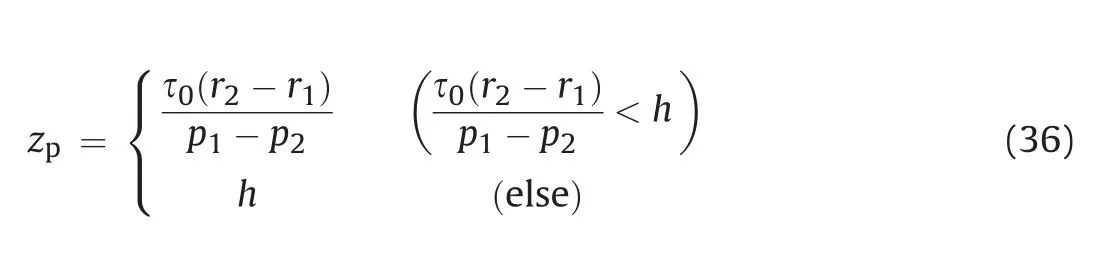




4. Results and discussion





5. Concluding remarks


 Journal of Rock Mechanics and Geotechnical Engineering2021年4期
Journal of Rock Mechanics and Geotechnical Engineering2021年4期
