Mesh generation and optimization from digital rock fractures based on neural style transfer

Mengsu Hu, Jonny Rutqvist, Carl I. Steefel

Energy Geosciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA, 94720, USA

Keywords:Convolutional neural network (CNN)Neural style transfer (NST)Digital rock Discrete fractures Discontinuum asperities Grain aggregates Mesh generation and optimization

ABSTRACT The complex geometric features of subsurface fractures at different scales makes mesh generation challenging and/or expensive. In this paper, we make use of neural style transfer (NST), a machine learning technique, to generate mesh from rock fracture images. In this new approach, we use digital rock fractures at multiple scales that represent‘content’and define uniformly shaped and sized triangles to represent ‘style’. The 19-layer convolutional neural network (CNN) learns the content from the rock image,including lower-level features(such as edges and corners)and higher-level features(such as rock,fractures,or other mineral fillings), and learns the style from the triangular grids.By optimizing the cost function to achieve approximation to represent both the content and the style,numerical meshes can be generated and optimized. We utilize the NST to generate meshes for rough fractures with asperities formed in rock, a network of fractures embedded in rock, and a sand aggregate with multiple grains.Based on the examples, we show that this new NST technique can make mesh generation and optimization much more efficient by achieving a good balance between the density of the mesh and the presentation of the geometric features. Finally, we discuss future applications of this approach and perspectives of applying machine learning to bridge the gaps between numerical modeling and experiments.

1. Introduction

Fractures play key roles in subsurface energy recovery and storage,including hydrocarbon and geothermal energy production,and nuclear waste disposal. Fractures, with sizes ranging from microns to kilometers,may act as conduits or seals for fluid flow in these various subsurface energy activities (Rutqvist and Stephansson, 2003), and thus it is essential to have a good understanding of their potentially dynamic features with good representation of their geometric features.

Based on geometric features, fractures can be categorized into three different scales: discrete thin fractures, rough fractures with certain widths and with asperities (may or may not be filled with minerals),and microscale grain assemblies and asperities(Hu et al.,2017a; Hu and Rutqvist, 2020a,b, 2021). At reservoir scales, fractures often appear in groups, arbitrarily oriented and intersecting with each other, thus forming a network. These fractures are usually very thin (e.g. microns to millimeters) relative to their length(meters). When a single fracture is examined more closely, it is often rough and may be filled with minerals and connected to smaller fractures in the surrounding rock. Zooming into the microscale, a single fracture becomes a rough channel with asperities made up of a number of tightly contacting mineral grains.

Mesh generation is an essential first step in numerical modeling of fractures and rock matrix at any of these aforementioned scales and can be challenging and/or expensive. At the discrete fracture scale, arbitrarily oriented and intersected fractures may lead to a great number of unevenly sized blocks that have many sharp corners. A number of mesh generators have been developed for discrete fracture networks (e.g. the well-known dfnWorks developed by Hyman et al.(2015)).However,it is challenging to consider a large number of fractures embedded in rock matrix. At the microscale, these asperities create surfaces that are not smooth.Because of the challenges associated with dynamics of contacts between a number of arbitrarily shaped blocks, only rarely can a mechanical model be applied at this scale(Hu and Rutqvist,2020b).More widely, fluid flow, transport and/or reaction are often modeled at this scale (Al-Yaarubi et al., 2005; Zou et al., 2015;Steefel,2019),in which case the most common meshing technique is to use rectangular elements to map the rough fracture channels.

Convolutional neural network(CNN)is one of the deep learning approaches that has been widely applied to image recognition(Simonyan and Zisserman, 2015; Babhulgaonkar et al., 2020;Rabbani et al.,2020).When a CNN model is trained to recognize an image, each feature from the input image can be extracted by an image filter (a layer), and this several-layer filtered information is propagated toward the output layer so as to form a filtered version of the image with original ‘content’ (e.g. geometry). By combining CNN for content and style presentation of texture information,Gatys et al. (2015) invented neural style transfer (NST) to create new art images. This was achieved by optimizing the approximation of a ‘content’ with texture of a ‘style’ by constructing a loss function as a weighted average of the loss functions of content and style.Since its invention,NST has drawn considerable interest as a new approach for creating art artificially. However, this approach has never been applied in science or engineering.

In this paper, we will make full use of the NST by combining digital rock fractures at multiple scales that represent‘content’with numerical meshes that represent‘style’.We will first introduce the approach and the structure that we used for the NST calculation.Then we apply the NST to generate meshes for rough fractures with explicit asperities formed in rock,a network of fractures embedded in rock, and a sand aggregate with multiple grains. Finally, we discuss future applications of this approach.

2. Approach

2.1. Machine learning and numerical modeling

Machine learning has been an increasingly popular research approach that has been applied in disciplines ranging from social science to natural sciences, geosciences (Karpatne et al., 2019;Dumont et al., 2020; Mital et al., 2020), and engineering in recent years. The approach benefits from the flexibility and generality of using statistics and algorithms that enable computers to learn without explicitly programming the physics.

When the desired output is given,for example by measurement,synthesis, or results produced by other approaches such as numerical modeling, a general statistical distribution (linear, polynomial, logistic, Gaussian, or their combination) can be learned.This is called supervised machine learning. When the desired output is not given,the machine learns the pattern of the data and finds the trend by itself. This is called unsupervised machine learning. Linear and nonlinear data distribution functions lead to continuous solutions,as desired in regression problems.In contrast,logistic regression in combination with a set of discontinuous functions may lead to a number of discontinuous numbers that determine the decision boundaries. This type of problem is categorized as a classification problem.

A typical supervised machine learning algorithm involves the following steps:

(1) Construct the hypothesis (a guess of the output). These possible hypotheses include the aforementioned linear, polynomial, logistic, Gaussian, or a network that combines these functions (known as a neural network):

where h represents the hypothesis;x is the matrix of the input data with a number of features and a number of examples;and θ is the vector of weight factors that need to be determined,which function as fitting coefficients of the distribution constrained by the available datasets for a given output.

(2)Construct the cost function,which can be understood as the cost of deviation of a hypothesis from the given output:

where f is the function of deviation of h from the given output y.For a linear regression problem, it becomes

If using regularization to enhance convergence, the cost function adds:

and the cost function becomes

where λ is the penalty factor to prevent overfitting.

(3)Based on Eq.(2),the solution of each component of θ can be found by minimizing the cost function:

where the superscript k refers to the iteration number, the subscript j refers to the jth feature,and μ is the learning rate.

(4) Repeat steps (1)-(3) until the fitting coefficient vector θ reaches convergence.A simplified schematic of machine learning is shown in Fig.1.

Fig.1. Schematic of machine learning.

Based on the features generalized above, the following similarities can be found between machine learning and numerical modeling, as listed in Table 1.

Table 1 Theoretical comparison between numerical modeling and machine learning.

In Eq. (7), wTrepresents the shape function,φ is the field variable at interpolation units, and φ is the field variable. Eq. (7) represents a typical linear interpolation that may be used in different numerical methods such as finite element, finite difference, finite volume, and numerical manifold methods. Comparison between these numerical methods in terms of interpolation was made by Hu and Rutqvist (2020a). Similarity between linear interpolation in numerical modeling and linear hypothesis in machine learning is made explicit if Eqs. (7) and (12) are compared.

Eq. (8) represents higher-order interpolation with a larger number of degrees of freedom (DOFs). These include: (1) Formulation 1: increasing the number of interpolation nodes leading to high-order weight functions;and(2)Formulation 2:increasing the order of interpolation units from a constant value while keeping the same weight function (Wang et al., 2016). Comparing Eqs. (7)and (13), we find that if the function g is linear, then this type of hypothesis resembles the second formulation of higher-order interpolation. Eq. (13) will be explained in more detail in Section 2.2.

Eq. (9) represents the total potential energy function for maintaining the balance of solid and/or momentum, and/or mass considering all types of boundary constraints(Hu et al.,2017b)for numerical modeling.Similarly,the cost function as expressed in Eq.(2) represents the cost of deviation between a hypothesis and the given output. If the linear interpolation is based on physical laws,similarities can be further found with the expanded versions of total potential function for numerical modeling and cost function for machine learning.

In order to apply boundary constraints, the penalty method is often used by giving a large penalty number to penalize deviation from a certain boundary constraint. Similarity between this with the regularization term in the cost function is made explicit if Eqs.(4) and (10) are compared.

Finally,in order to solve the equation in numerical modeling,the total potential energy is minimized to represent equilibrium. One approach to derive the solution for nonlinear equation is to use Newton-Raphson iteration as expressed in Eq. (11). Similarly,gradient descent is a common way to minimize the cost function for machine learning so that the most accurate values of θ can be gradually learned, while the most accurate hypothesis h can be achieved for a given set of values of y.In this study,because we use a rather deep neural network,the Adam optimization algorithm as a first-order gradient-based algorithm is applied for optimization(Kingma and Ba, 2015).

To summarize, similarities between numerical modeling and machine learning can be found if similar interpolation structures are used. The major difference is that in machine learning, the weighting factors in θ need to be derived while input data in x are given. In numerical modeling, x needs to be solved and weight factors are typically constructed by shape functions of numerical grids. If the physical meanings of x and θ are swapped, machine learning can be identical to numerical modeling in terms of constructing the hypothesis and cost function and minimizing the cost function to derive θ. Because of these similarities, computer software designed for machine learning and numerical modeling may be shared.

Whether machine learning or deep learning can be applied widely for physical analysis of geosciences depends on two important questions:

(1) If there is a lack of data,can machine learning perform like a numerical model?

(2) What can machine learning do to bridge the fields of experiments and numerical modeling?

The similarity between machine learning and numerical modeling derived in this section provides the theoretical demonstration that machine learning can function like a numerical model.In a recent study by Sirignano and Spiliopoulos (2018), machine learning was trained to solve partial differential equations,and thus functions like a physics solver. However, building on 60 years of experience in the development of numerical models for analyzing physics across temporal and spatial scales, numerical model supervised machine learning could be a promising pathway to integrate the advantages of both.

Between experiments and numerical modeling, there are at least two challenging steps: (1) image processing may require considerable effort when attempted using traditional approaches;and(2)determination of physical properties can be difficult.These challenges can be overcome with the help of machine learning. In addition, machine learning can be easily applied to predict statistical trends and to classify patterns.With the development of CNN,machine learning has been increasingly used in the fields of image processing, but prediction of the dynamic evolution of geometry can be challenging. Thus, machine learning supervised by experiments and numerical modeling may be a promising approach if there are sufficient datasets.

2.2. Convolutional neural network for image recognition

Deep neural networks make use of multiple layers of different types of functions to establish a highly nonlinear(or discontinuous)propagation of information from the input to the output. The general hypothesis of a deep neural network can be expressed as

where the superscript l refers to the total number of layers of a neural network.In Eq.(14),the hypothesis may involve a number of layers of linear or nonlinear algebraic transformation function g in different layers. If l = 2 (only two layers) and g(z) = z, this neural network is simplified as a linear regression problem;If l=2 and g is a sigmoid function, this neural network is simplified as a classification problem.

In most cases, however, the purpose of introducing multiple layers is to introduce additional orders for enhanced approximation, which is achieved when multiple layers are combined. These layers include an input layer, several hidden layers and an output layer. Therefore, such enhanced approximation is realized as Eq.(14),functioning like a propagation from the bottom to the top row.With increased number of layers, the function becomes highly nonlinear. Solving θ in each layer is challenging. Thus, backpropagation is used to solve θ from the output layer to the input layer.Embedded in the steps of a typical machine learning routine,a neural network consists of a forward propagation routine to construct the hypothesis and a back-propagation routine to approximate θ until convergence is realized.

In the field of image recognition where images are represented by pixels, the input data are represented as a tensor, i.e. image height×image width×color depth.CNN has been widely used for processing these data and recognizing features. Different types of CNN have been developed to accommodate different types or sizes of data.Fig.2 shows a CNN that consists of several layers to classify rock matrix and fractures from an image. In this CNN, different layers can be used to realize higher-order approximation and matrix transformation with multiplication of a number of different functions. These layers include convolutional, rectified linear unit(ReLU), normalized exponential (softmax), pooling, and fully connected layers. The structure of the VGG-19 network used in this study was introduced by Simonyan and Zisserman (2015).

2.3. Neural style transfer

Based on image recognition, NST was invented by Gatys et al.(2015) to create new art images by combining CNN for content presentation with style presentation of texture information. Thus,the NST generates images that match the content and style of the content and style images, respectively. This is achieved by constructing a total cost function J consisting of weighted average of the content cost function and the style cost function:

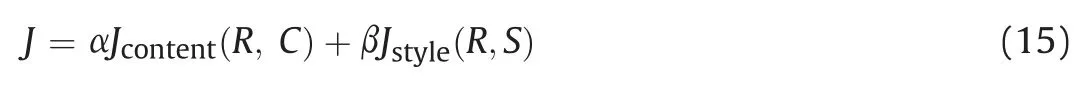
where R,C and S represent the functions associated with generated(resulted), content and style images, respectively. The weighting factors α and β are user-defined.

In order to approximate the content image,the cost function of a certain selected hidden layer is

where h, w and n mean the height, width and the total number of channels of this hidden layer, respectively. This hidden layer therefore has a function(activation)a with a dimension of h× w×n.

In order to properly represent the ‘style’ in an image,the inner product (that projects one vector on another to represent similarity) is used to define the style matrix:

The cost function for the style is the weighted average of cost function of each layer:

where ςkis the weighting factor of layer k,satisfyingsimplicity, evenly distributed weighting factors among different layers can be used. With this specially constructed cost function involving both content and style images, we are able to generate new images that keep the content of the content image and the style of the style image.

Considering that the VGG-19 model (Simonyan and Zisserman,2015) has been trained on very large image datasets, we apply the 19-layer VGG network to conduct our NST simulation for mesh generation. In this network, the shallower layers are designed to detect lower-level features such as edges and corners. The deeper layers are used to detect higher-level features such as rock, fractures,or other mineral fillings.The structure and schematics of the NST model for mesh generation are shown in Fig.3,in which a 19-layer VGG network is included in the middle. As shown in Fig. 3,because this approach for generating mesh is based on machine learning the content of the rock images and learning the style of the mesh,the only data required for the mesh generation are the image of the content (rock image) and the image of the mesh style. The learning process is indeed an optimization process from an initially generated noisy image to the finally generated image that achieves the minimized total cost, and thus has the best approximation to the content of the rock image with the mesh style.Optimization of the total cost function is realized by using the Adam optimization algorithm (Kingma and Ba, 2015).

Fig. 2. CNN for recognizing rock matrix and fractures.

3. Examples and results

To demonstrate the approach, we use the NST model with the 19-layer network to generate numerical meshes for various systems of interest in the geosciences. We extracted images of rock fractures at different scales to provide the contents for the examples. These include an image that contains several dominant and rough fractures, an image that contains a network of densely intersecting discrete fractures, and an image that contains an aggregate of sandstone grains.In order to understand how the NST works and to avoid additional complexity that is introduced by the complexity of the style,we have used uniform triangles in terms of size,shape and distribution as the style images to explore this use of machine learning for mesh generation.

3.1. Example 1: Mesh generation for rough fractures using neural style transfer

As a first example, we utilized the NST algorithm to generate meshes for an image of rock containing several dominant and rough fractures.We tried two different densities of triangles as the style.Fig.4 shows the results.As can be noted,the NST learned the boundaries of rock and fractures from the rock image and applied the triangular styles to the images that were recognized. The sizes of triangles in the generated mesh are the same as those in the style image. With the size and shape of the triangles kept in the generated image, the machine rearranged the orientations of the triangles to accommodate the fractures and rock matrix. Comparing the generated meshes with coarse triangle style (top) and dense triangle style (bottom), we can see that the machine is ‘smart’enough to distribute triangular grid cells along fractures even with coarse triangles.

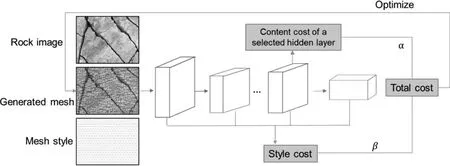
Fig. 3. NST model for mesh generation from a rock image.

Fig. 4. NST generated mesh for rough fractures: Coarser (top) and denser (bottom) meshes.

Fig. 5. NST generated mesh for rough fractures with denser meshes and thicker mesh lines.

However, the mesh generated using the denser meshing style is notclear-suggesting insufficient resolutionof thestyleimage.In order to resolve this issue,we used a new style image with the same density of the mesh but with thicker mesh lines.The result is shown in Fig.5.Despite thatsome elements are not perfectly triangularinFig.5 due to non-triangular meshes on the boundaries in the style image,we can see that the mesh generated with the thick-line style becomes clearer than the one shown in Fig.4.

In order to analyze the differences caused by the thickness of the lines in the mesh style, we plot the changes of cost functions over iterationsinFig.6.InFig.6a,weshowthechangesof totalcost,content cost and style cost corresponding to the thin-line style (Fig. 4). In Fig. 6b, the changes are corresponding to the thick-line mesh style(Fig.5).Bothimagesare400 pixelsby300pixels-suchlowresolution is used for only demonstrating the approach with smaller computational effort. For both cases, we used α = 10 and β = 40. By comparing the changes,we can see larger content and style costs for the thick-line style, leading to a higher total cost. However, with increased number of iterations,a larger decrease can be found in the thick-line style.The total cost does not reach a convergence value(a rate larger than zero) until 200 iterations for the thin-line style.However,the total cost reaches convergence after 150 iterations.

From this example, we see that because the generation is automatic despite the complexity of the geometric features, this new NST technique can potentially save a great deal of effort for mesh generation and optimization by achieving a good balance between the density of the mesh and the presentation of the geometric features.From the comparison between the low-resolution thin-line and high-resolution thick-line style images, we show that it is important to provide a good balance of resolutions between the content and the style images.

3.2. Example 2:Mesh generation for discrete fractures using neural style transfer

In the second example,we test the NST algorithm with a densely intersecting fracture network (Fig. 7). This image contains more than 50 densely intersecting fractures,including a long and sinuous fracture running from the left to the bottom of the domain.We used the coarse triangles as style.It can be observed that the NST model captures all the fractures and arranges the triangles along the intersecting fractures. In particular, if we examine the long and rough fractures, we see that all the non-smooth line segments are well represented in the generated mesh.

3.3. Example 3:Mesh generation for a sandstone core sample using neural style transfer

In the last example,we test the NST algorithm with a sandstone core sample (Fig. 8). The major difference between this example and the previous two examples is that the boundaries of the grains in this example are not as apparent as those of the fractures in the previous two examples. This makes it more difficult for the machine to learn the higher-level content. It is apparent that because of the difficulty associated with learning of the content,the mesh is distributed well but the boundaries of the grains are not very clear.Increasing the density of the triangles does not resolve the issue.Therefore, this issue is associated with content learning, and may be addressed by improving the resolution of the content image,and/or by improving the neural network for content learning.

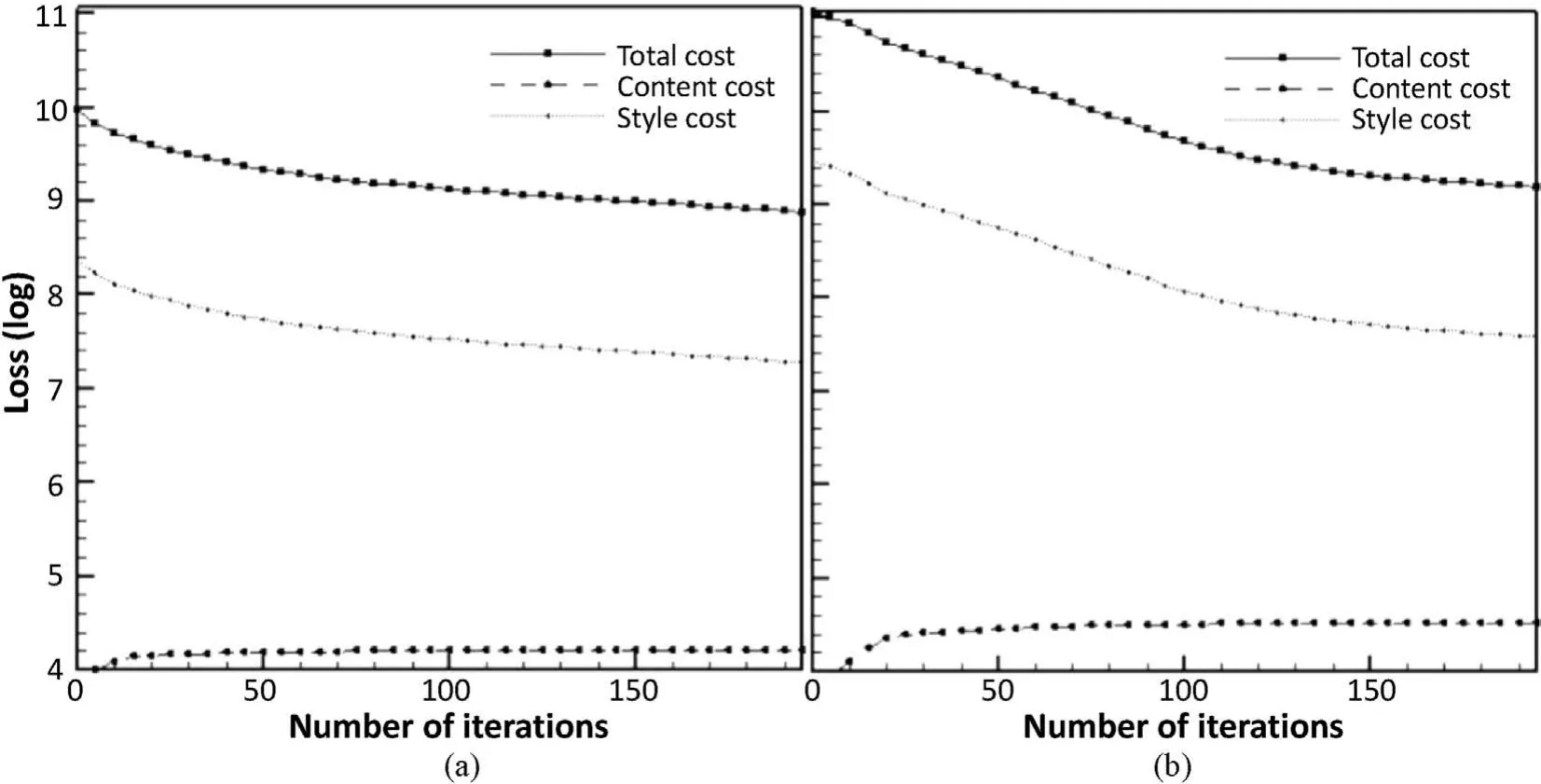
Fig. 6. Cost functions decreasing with iterations by (a) thin-line and (b) thick-line mesh styles.

Fig. 7. NST generated mesh for discrete fractures.

Fig. 8. NST generated mesh for a sandstone core sample.

4. Conclusions

In this study,we have made use of NST by combining digital rock fractures at multiple scales that represent‘content’with numerical meshes that represent ‘style’. We used a 19-layer VGG network to conduct our NST simulations, where the shallower layers are designed to detect lower-level features(such as edges and corners)and the deeper layers are used to detect higher-level features such as rock, fractures, or other mineral fillings. By optimizing the cost function to achieve approximation to represent both the content and the style,numerical meshes were generated and optimized.

We applied two different densities of triangles as style images to a rock sample with rough fractures.By using NST,we can generate a rather coarse mesh with the coarse triangle style. We also applied the NST to generate meshes for discrete fractures and at the grainscale for a sandstone core sample. Good representation of the geometric features with a rather coarse triangle style was achieved in both examples. From the comparison between the low- and high-resolution style images, we show that it is important to provide a good balance of resolutions between the content and the style images. Based on the examples, we show that this new NST approach for mesh generation is automatic.This new approach can potentially make mesh generation and optimization much more efficient,with the result that a good balance between the density of the mesh and the representation of the geometric features can be achieved.

The new approach presented in this paper can be widely applied to mesh generation of complex geometric features.The mesh style that we used with triangles can be used for finite element analysis.In the future, rectangles and spheres can be used as styles to generate meshes for other numerical methods, such as finite difference and discrete element methods. In addition, adaptive mesh refinement can be explored with non-evenly sized triangles/rectangles as styles. Combined with three-dimensional (3D) digital rock images (if available, and data from images are sufficient), the challenges associated with 3D mesh generation may be overcome.Because the mesh generation routine is automatic, the NST technique is very promising for application of simple mesh patterns(e.g. evenly sized or adaptively refined triangles, rectangles, and spheres) to generate and optimize meshes for complex geometric features in the geosciences.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The first author would like to thank Andrew Ng for teaching the enlightening online courses including Machine Learning, Neural Networks and Deep Learning, Convolutional Neural Networks,Sequence Models. This research was supported by Laboratory Directed Research and Development(LDRD)funding from Berkeley Laboratory, and by the US Department of Energy (DOE), including the Office of Basic Energy Sciences,Chemical Sciences,Geosciences,and Biosciences Division and the Office of Nuclear Energy, Spent Fuel and Waste Disposition Campaign,both under Contract No.DEAC02-05CH11231 with Berkeley Laboratory.