A state-of-the-art review of automated extraction of rock mass discontinuity characteristics using three-dimensional surface models

Rushikesh Bttulwr, Msoud Zre-Nghdehi, Erhim Emmi, Jvd Sttrvnd

a Department of Mining and Metallurgical Engineering, Mackay School of Earth Sciences and Engineering, The University of Nevada, Reno, NV, 89557, USA

b Department of Computer Science and Engineering, The University of Nevada, Reno, NV, 89557, USA

Keywords:Rock mass Discontinuity characterization Automatic extraction Three-dimensional (3D) point cloud

ABSTRACT In the last two decades, significant research has been conducted in the field of automated extraction of rock mass discontinuity characteristics from three-dimensional (3D) models. This provides several methodologies for acquiring discontinuity measurements from 3D models, such as point clouds generated using laser scanning or photogrammetry. However, even with numerous automated and semiautomated methods presented in the literature, there is not one single method that can automatically characterize discontinuities accurately in a minimum of time. In this paper, we critically review all the existing methods proposed in the literature for the extraction of discontinuity characteristics such as joint sets and orientations,persistence,joint spacing,roughness and block size using point clouds,digital elevation maps, or meshes. As a result of this review, we identify the strengths and drawbacks of each method used for extracting those characteristics. We found that the approaches based on voxels and region growing are superior in extracting joint planes from 3D point clouds. Normal tensor voting with trace growth algorithm is a robust method for measuring joint trace length from 3D meshes. Spacing is estimated by calculating the perpendicular distance between joint planes. Several independent roughness indices are presented to quantify roughness from 3D surface models, but there is a need to incorporate these indices into automated methodologies. There is a lack of efficient algorithms for direct computation of block size from 3D rock mass surface models.

1. Introduction

Discontinuities play a significant role in stability of slopes, and most of the stability analysis methods for highwalls rely on measurement and characterization of the geological discontinuities,since they define the weak planes in a rock mass along which the rock blocks detach and fail(Jaboyedoff et al.,2009;Kainthola et al.,2015).Decisive information on rock joints also helps to predict the flow of groundwater, improve the quality of blasting in open pit mine highwalls, and finally provide a better stability condition for slopes (Zare Naghadehi et al., 2013; Zare and Jimenez, 2015).However, acquiring accurate geological information is mostly dependent on the field measurements, such as scanline mapping with a geological compass near steep rock slope faces.Occasionally,surveyors use a laser scanner mounted on a vehicle to scan the rock face and utilize special software in the office to make the measurements digitally on a computer. In contrast, the long-range radar/laser scanner cannot be employed for rock mass characterization due to the low resolution of generated point clouds. Therefore, the current practice approaches present numerous problems. Firstly, apart from being a laborious procedure, the access often does not exist to the rock faces to carry out geological mapping either in person or by a scanner. Additionally,there is a huge variation in the measurements at different locations of the mine,and it is difficult to accurately estimate the orientation and geometry of geological structures at few sample locations

where a scanline crosses the structure. Furthermore, in-person mapping with a compass at the base of a steep slope or driving on such an environment exposes people to multiple types of hazards. Finally, as the mine is being developed, new measurements are required since the slope faces are drastically changed due to new production blasting practices.

Algorithms developed to use three-dimensional(3D)models of slopes, such as point clouds or surface meshes, for mapping the geological discontinuities can address most of the above-mentioned problems.These algorithms may be helpful with performing larger quantities of measurements on a rock slope including inaccessible areas with much less efforts compared to the manual measurements.The subjectivityof evaluations is lesser in this waysince more data points on the slope are collected and the analysis is performed on the entire rock surface instead of a few scanlines preferred by the geologists.Additional measurements can be conducted at any time to refine the evaluation or solve ambiguities of interpretations(Ferrero et al., 2009). Further, automated analysis of rock slopes using 3D models is cheaper than traditional survey scanning in terms of operational cost and time (Slob et al., 2005). Feng and Röshoff(2015)presented a survey of laser scanning techniques for site characterization of rock faces.Abellán et al.(2014)conducted a review of publications related to the use of terrestrial laser scanners for rock slope characterization, rock slope monitoring, and other applications. However, the previous study does not include more advanced and recent research in the field of automatic characterization of discontinuities. Further, it does not include the studies related to aerial photogrammetry-generated 3D models that are highly applicable today for slope monitoring purpose. Therefore,there is a need to conduct a more comprehensive review.

The next section of the paper presents the various techniques for the acquisition of 3D models of slopes such as point clouds or triangular meshes. The International Society for Rock Mechanics(ISRM) (ISRM, 1978) outlined a number of parameters for geometrical, mechanical, and hydraulic characterization of discontinuities, including orientation, spacing, persistence/trace length,roughness,aperture,wall strength,filling,seepage,number of sets, and block size. The main part of this paper reviews the efforts on the partial or full automation of extraction of six discontinuity parameters, including joint sets, orientation, joint continuity (or trace length), spacing, face irregularity, and block size. Note that in this study, the terms ‘joints’ and ‘discontinuities’are used interchangeably.

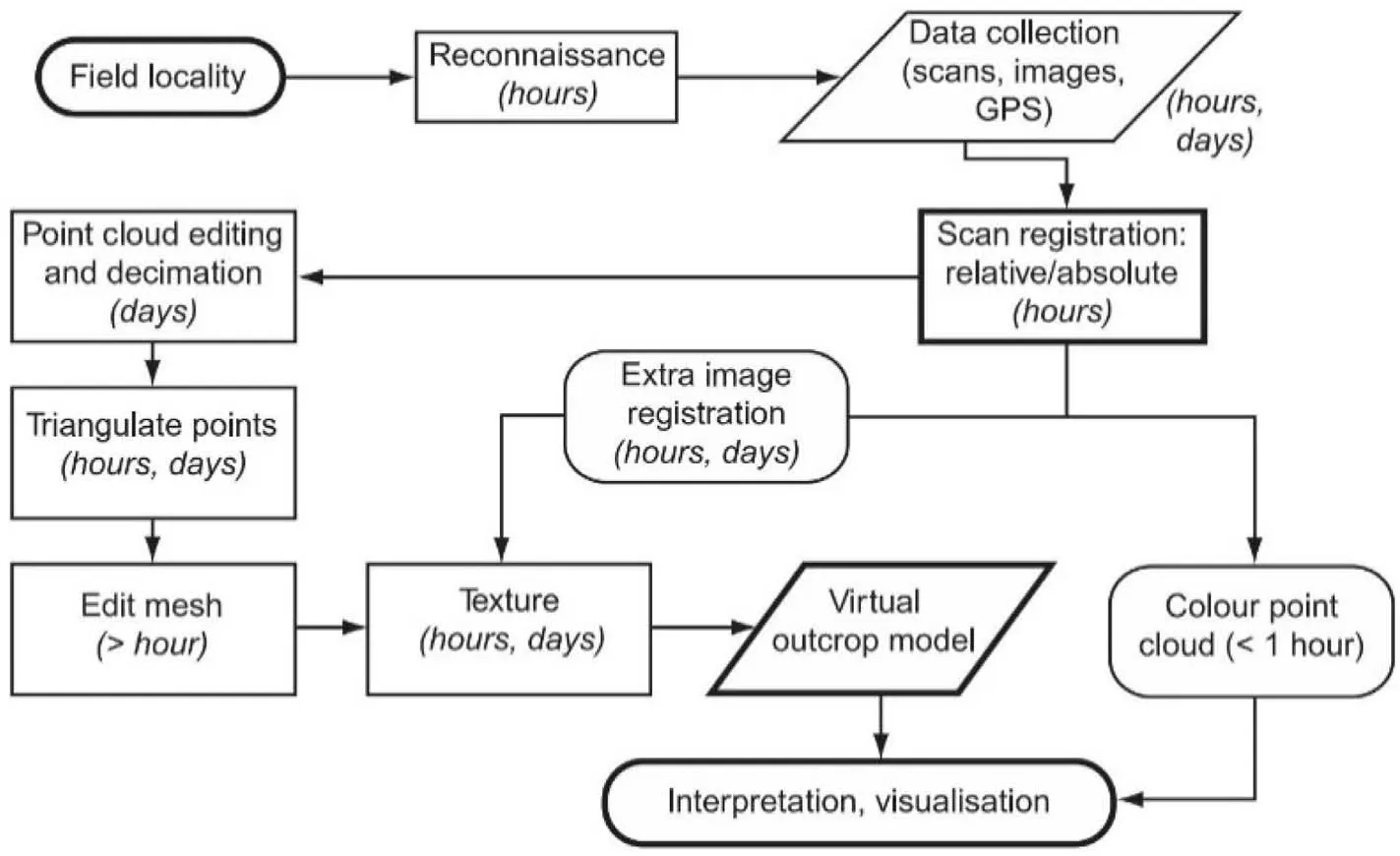
Fig.1. Workflow of laser scanning of rock masses (Buckley et al., 2008).

2. Data acquisition methods

Reliable extraction of discontinuities from 3D models mostly depends on the quality of the models and the method of data acquisition. For the successful implementation of an automated analysis, the data acquisition procedure should cover every significant discontinuity, need less overall cost and time than a traditional survey, and provide direct access to the slope with adequate positional accuracy in the model (Ferrero et al., 2009).

2.1. Laser scanning

A light amplification by stimulated emission of radiation(laser)scanner is mainly used to create accurate and precise highresolution digital elevation models (DEMs) in raster grids or triangular meshes or 3D point cloud. There are two types of laser scanning techniques depending on the position of the sensor,including airborne laser scanning (ALS) and terrestrial laser scanning (TLS). Most ALS and TLS used for ground measurement are based on the pulse method which uses the time of flight of laser pulse to calculate distances. Fig. 1 summarizes the workflow and average time requirements for the acquisition of point cloud data of a rock slope using TLS.Armesto et al.(2009)used the TLS-measured points to characterize the geometrical parameters for stability analysis of a granite boulder. They identified four issues that need to be considered while planning data collection using laser scanners: (i) location, (ii) number of stations to overcome occlusions,(iii) resolution, and (iv) reference system. TLS is also used for detecting rockfalls in an urban area by comparison of point clouds collected at different times (Abellán et al., 2011). Fig. 2 depicts the Leica RTC360 which is a high-performance 3D laser scanning system.

Fig. 2. Leica RTC360 3D laser scanner (Leica Geosystems, 2020).

Riquelme et al. (2017) performed an analysis comparing the results of discontinuity characteristics acquired using TLSgenerated point cloud and unmanned aerial vehicle (UAV) datagenerated point cloud, and found out that TLS data are more reliable. Further, the TLS category is found to be more accurate when the joint planes are not defined by enough planar points. Abellán et al. (2006) conducted a detailed study of rockfall using data from a long-range TLS.It enabled the collection of millions of points accurately in a few minutes.This study showed the ability of TLS to obtain reliable 3D displacement information over a large,unstable area (Oppikofer et al., 2009). The application of TLS for rock mass discontinuity characterization has been reported in numerous works in the literature(e.g.Fardin et al.,2004;Slob and Hack,2004;Bellian et al.,2005;Jaboyedoff et al.,2007;Olariu et al.,2008a;Lato et al., 2009; Sturzenegger and Stead, 2009a; Abellán et al., 2011;Gigli and Casagli,2011;García-Cortés et al.,2012;Vöge et al.,2013;Mavrouli et al.,2015).

Careful planning is essential to perform a TLS survey.Geological engineering field studies are conducted at a number of scales and distances;thus,it is necessary to plan ahead for required accuracy and precision mapping, scan resolution, and set-up of the scanner(Sturzenegger and Stead,2009a).There is a need to take scans from multiple locations to avoid the occurrence of horizontal and vertical occlusions. Also, the position of the scanner must be elevated for better data quality and signal intensity. The data also have to be registered into the coordinate system. The 3D laser scanning is an expensive technique to be utilized for collecting 3D data of rock mass(Riquelme et al.,2017).A comparison of different parameters associated with data collection using a TLS and aerial photogrammetry is presented in Table 1. It is evident that laser scanning is a costlier method in terms of data acquisition and processing time.Moreover, the processing of LiDAR data usually involves considerable user input whereas photogrammetry-derived point cloud generation is mostly automatic.

Table 1 Comparison of laser scanning and UAVs and photogrammetry data collection methods (after Cawood et al., 2017).

2.2. UAVs and photogrammetry

The recent availability of ready-to-use UAVs as well as the advent of structure from motion(SfM)(i.e.digital photogrammetry software) have led to the increased application of UAVs for geohazard analysis(e.g.Lee and Choi,2015;Al-Rawabdeh et al.,2016;Car et al., 2016; Suh and Choi, 2017; Battulwar et al., 2019; Peik et al., 2020; Winkelmaier et al., 2020). There are various types of sensors that can be integrated into a UAV such as visible-band,near-infrared and multi-spectral cameras, hyper-spectral cameras,thermal imaging, laser scanners, and synthetic aperture radar. A summary of each type has been presented in Colomina and Molina(2014). Fig. 3 highlights the important components and workflow in the methodology for generating 3D models using drones and photogrammetry.

The main reason for the augmented application of UAVs in Earth science industry can be attributed to the availability of low-cost drones with an at least 12 megapixel imaging sensor as cheap as 1000 US dollars(DJI,2020a).The use of UAV with a high-resolution camera is significantly less expensive than a TLS unit,both of which generate almost similar point cloud data. Even with a lowresolution UAV, the authors have proposed a methodology for generating high-resolution 3D models for open pit mine slopes(Battulwar et al.,2020a). Further, the deployment of UAVs and the collection of images is a very simple process because of the availability of an array of commercial mobile applications for autonomous flight planning. Another advantage of using UAVs for rock mass mapping is the ability to collect high-quality images of rocks from a range of perspectives such as plane view,front oblique view,and side view,as well as close proximity views from a safe distance.This capability makes this technique superior to laser scanning in terms of safety and the capacity to map large size outcrops.Most of commercially available quadcopters weigh less than 2 kg which can be carried in a backpack (Zekkos et al., 2018). All these reasons make the UAVs ideal tools for remote collection of 3D data from rock masses. Several studies have successfully demonstrated the application of UAV photogrammetry for rock mass characterization(e.g.Bemis et al.,2014;Vasuki et al.,2014;Greenwood et al.,2016;Vollgger and Cruden,2016;Salvini et al.,2017).Fig.4 shows the DJI Matrice 600 Pro UAV fitted with a digital camera and dual-real time kinetic (D-RTK) GNSS for high-precision flights.

Fig. 4. DJI Matrice 600 Pro rotary-wing UAV (DJI, 2020b).

Although the use of UAVs is relatively easy, generating a highresolution and accurate 3D model of rock mass requires a reasonable amount of experience and skills.The resolution and quality of the point clouds from UAV imagery depend on the relative height of the drone above ground, size of the imaging sensor, and an adequate proportion of overlapping between images(Di Franco and Buttazzo, 2016; Suziedelyte Visockiene et al., 2016). This process also requires the deployment of GCPs in sufficient numbers that are distributed over the mapping area uniformly. The use of GCPs significantly improves the positional accuracy and scale of the 3D model (Martínez-Carricondo et al., 2018). Now, laying GCPs on steep ground is difficult because of accessibility limitation that is always the case in discontinuity characterization of open pit mine slopes. This problem can be solved using a slightly expensive solution that involves the use of double GNSS receivers and making PPK or RTK correction.

Once the collection of images is done,the data are processed in a photogrammetry software to generate the 3D models such as point clouds, meshes, digital elevation maps and orthomosaic maps.Table 2 lists the major photogrammetry software available in the market for professional and academic use. The process takes between a couple of hours to days depending on the number and resolution of photos as well as the computational power of the personal computer. Currently, companies such as Agisoft, Pix4D,Autodesk, and Bentley offer cloud processing feature that is relatively faster and saves hardware costs. However, mapping of a typical rock face takes between 100 and 500 pictures that should be completed within a day(Vasuki et al.,2014;Salvini et al.,2017).The process of aerial imaging is also obstructed by bad weather conditions such as rain or high winds, and the image quality can practically be diminished by the existence of the snow. Also, the position of the sun affects the number of shadows in the images,which may in turn create noise in the 3D models.The use of drones for non-recreational activities is regulated by federal agencies around the world such as the Federal Aviation Administration(FAA)in the USA. Some of the regulations include the maximum flight altitude, which is 120 m, only line-of-sight operations, no flights over people and vehicles, etc. However, these regulations are easy to follow and make the UAV operation safer.

Table 2 Photogrammetry software and cost as of December 2020.

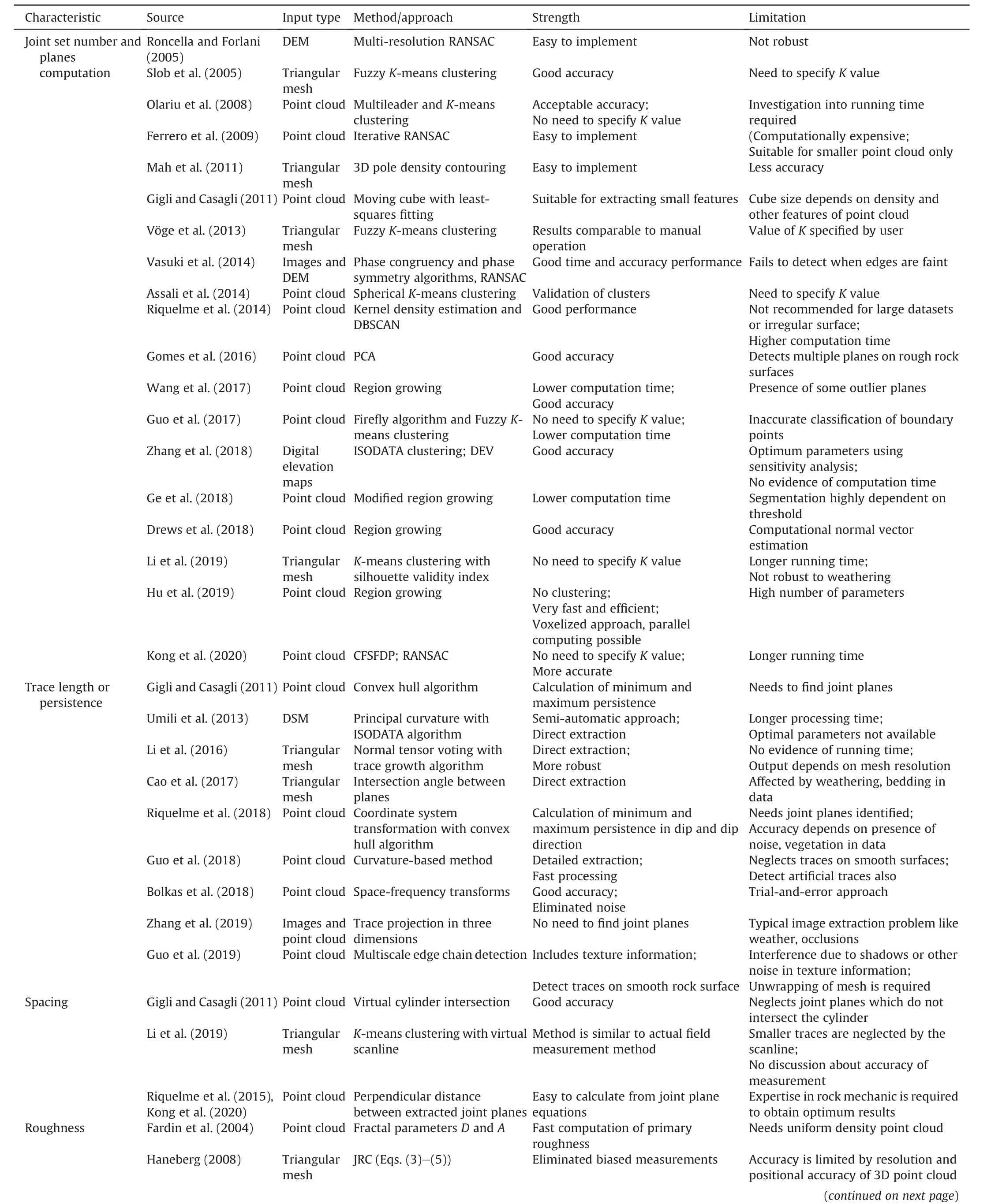
Table 3 Approaches for rock mass discontinuity characterization from 3D models with strengths and limitations.

Table 3 (continued)

For the purpose of acquiring a detailed and high-quality 3D model of a rock mass, the UAV is required to capture a sufficient number of overlapping pictures from all the directions, which is a challenge to accomplish using manual maneuvering of UAVs.Another challenge is the continuous change of terrain in open pit mines.For example,due to blasting and extraction operations, the shape of slopes could potentially change every day.Since the profile of the ground is undulating, it requires the drone to follow the profile to constantly acquire required resolution images. These problems cannot be overcome using conventional commercial applications that use a parallel flight planning routine. This shows that there is a requirement for the development of customized flight planning applications using advanced coverage path planning algorithms as shown in Bircher et al.(2016),where such a problem has been modeled as a 3D art gallery problem or a two-stage imaging methodology proposed by Battulwar et al. (2020b). Despite these drawbacks, it can be concluded that the application of UAVs for the collection of aerial images of the rock mass is a much safer,more efficient, and promising method.

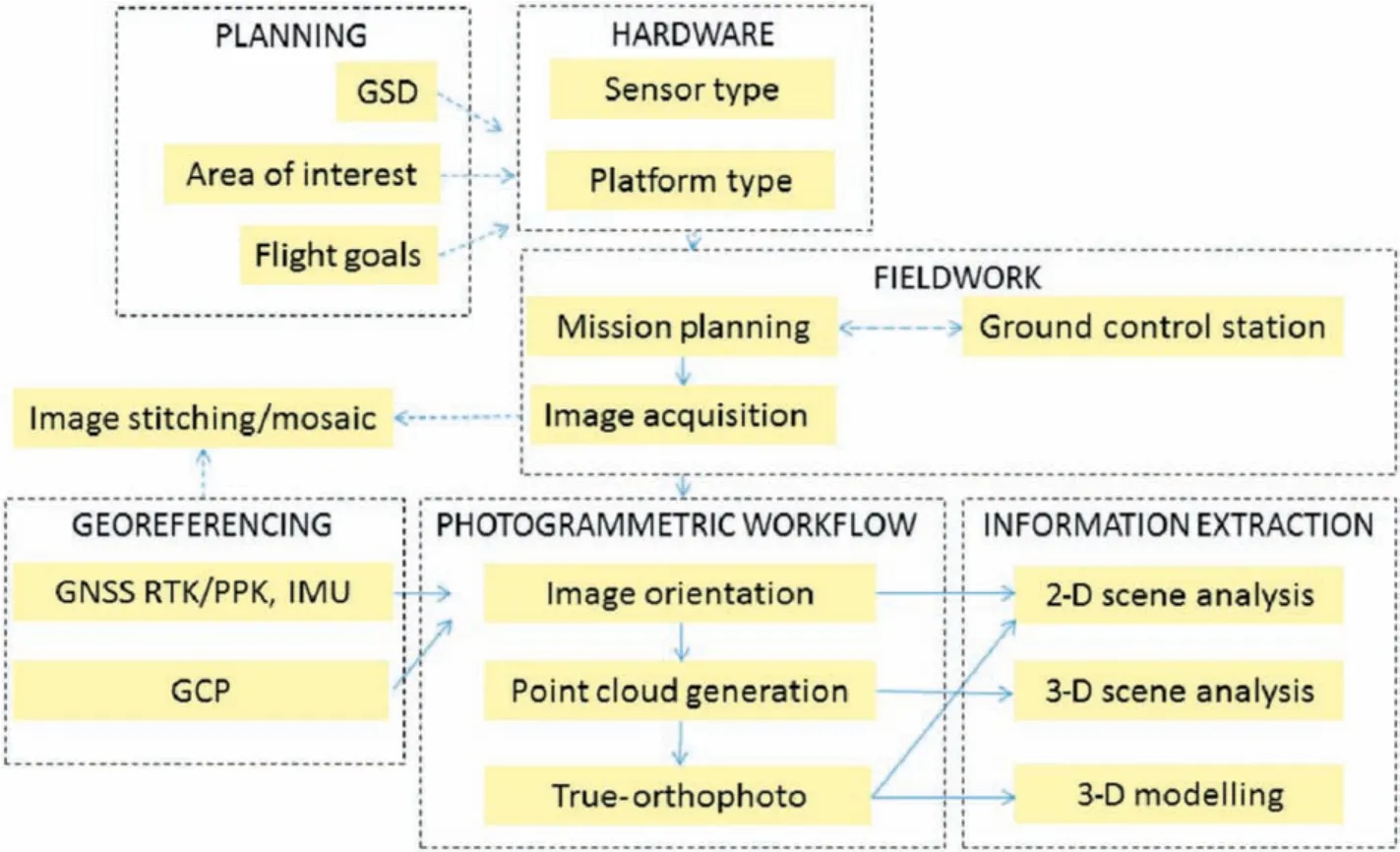
Fig.3. Workflow for generating 3D models using UAV and photogrammetry(Giordan et al.,2017).GSD-ground sample distance; GNSS-global navigation satellite system;RTKreal time kinetic; PPK- post processed kinematic; GCP - ground control point; IMU - inertial measurement unit.

3. Acquired discontinuity parameters

In this section, a brief survey of the works in the literature dealing with the extraction of rock mass discontinuity features including number and location of the joint sets, orientation,persistence, joint spacing, roughness, and block size, is presented.Firstly, all algorithms and methods presented in the literature are classified based on their parameter of interest. Secondly, a brief overview of the method, describing the procedure, is presented.Finally, their strengths and limitations are highlighted. The final goal of this analysis is to select procedures that can be used for developing an automated rockfall risk analysis system using UAVs.Thus, the procedures are reviewed based on their degree of autonomous operation and running time. For the same reason, in this paper, laboratory measurements of discontinuities based on drilling core samples are considered out of scope.

3.1. Joint sets and orientation

3.1.1. Clustering-based methods

Lato and Vöge(2012)presented a mesh-based software referred to as“PlaneDetect,”which extracts joint orientations by smoothing the mesh to remove noise in the first step,followed by identifying regions with coplanar points through the analysis of the angular difference between nodes.Each region was further analyzed by the same approach but different parameters for eliminating edge and blast-damage regions.Next,each coplanar region was classified as a discontinuity surface by comparing its area and average surface orientation variability with user-specified thresholds. Finally,discontinuity surfaces were clustered using fuzzy K-means algorithms where the value of K is set by the user. The user must also determine a total of nine parameters (eight thresholds and one K value) to render the accurate orientation of joint planes using this process.Despite such a high dependency on the user,the approach showed comparable results with manually mapped orientations.

The problem of working with mesh is that the quality depends on the process of triangulation and its resolution as small features could be neglected and complex shapes could lead to incorrect and distorted polygonal surfaces. Point clouds, on the other hand,provide amounts of information in terms of millions of points but are computationally expensive(Gigli and Casagli, 2011).

The semi-automatic approach,which uses visual interpretation,generates results that are mostly non-reproducible because different operators have different expertise or may use different identification criteria.Studies indicate that even the same observer does not reproduce the same results in the similar situations in multiple trials (Mabee et al., 1994). However, geological analysis using 3D data is a complex process that requires the interpretation of complex geometries and subtle textural changes. Such an analysis necessitates significant intuition as well as deductive and inductive reasoning of the user. Therefore, it is important to note that a semi-automatic approach with user interaction is useful to allow geologically feasible results. Methods for automatic clustering of discontinuities based on their orientation without consideration of priori probabilistic models are common to determine the number of joint sets in point cloud datasets. Assali et al.(2014) used K-means clustering to classify 3D point cloud points into different joint sets based on their normal vector similarities.Olariu et al. (2008) proposed a two-pass clustering method for estimating the mean orientation of joint sets. In the first pass, the multileader clustering was used to partition the point cloud into small clusters of which minimum and maximum sizes are defined by the user.The normal vector for each cluster was estimated using the principal component analysis (PCA). These clusters were partitioned into joint sets using K-means clustering algorithm where the optimal value of K is determined using a minimum description length (MDL) statistic (Barron et al.,1998). The orientation values measured from laser scanned rock mass point cloud using this method were reasonably accurate. Further, this method is completely unsupervised. However, the running time of method with respect to different sizes of point clouds needs to be investigated. Also, the effect of the parameters of multileader clustering method on the accuracy of measured orientation values is required.

Jimenez-Rodriguez and Sitar (2006) presented a spectral clustering algorithm which transformed the normal vectors for each point into a transformed K-dimensional space. The point coordinates in transformed space were given by eigenvectors of the normalized affinity matrix of normal vectors. The K-means clustering was used for determining the clusters in a transformed space. The original points were assigned to the clusters same as their transformed point. Unlike usual clustering, the advantage of performing clustering in transformed space is that the transformed points are tightly clustered around the cluster centers, which increases the speed and accuracy of the process. It has also been claimed that the results of spectral clustering are more natural partitions than other clustering methods.Fuzzy K-means clustering performs a better clustering assignment compared to a non-fuzzy clustering method and was integrated with the spectral clustering algorithm by Jimenez(2008).The results were more accurate relative to spectral clustering solely using the K-means algorithm.However, the application of these techniques requires the prior knowledge of the value of K, i.e. the total number of clusters. Slob et al. (2005) used a fuzzy K-means clustering method directly with the orientation data for each facet of the mesh model for automatically clustering discontinuity sets. The clusters outliers were removed by iteratively using the Fisher’s K value and selecting the cluster size with maximum K value. The working of the commercial software Split-FX(Split Engineering LLC.,2020)is based on this method. Van Knapen and Slob (2006) automated the above method by determining the optimal value of clusters using cluster validity indices given by Hammah and Curran (2000). Guo et al.(2017) further improved this method with the use of Firefly algorithm(Yang,2009)to determine optimal locations of initial cluster centers for the fuzzy K-means algorithm and applied it to 3D point cloud data. They also segmented the raw point cloud into equalsized cubes or octree partitioning and fitted a plane to each cube(using PCA) to determine its normal vector before clustering. This preprocessing step greatly reduced the computation time of the algorithm.

Chen et al.(2016)proposed a method for automatic clustering of mesh facets into joint sets using an improved K-means clustering algorithm. It was based on using sample density to find the initial clusters and the average silhouette validity index (Rousseeuw,1987) to estimate the optimum value of K. Silhouette validity index determines the validity of clusters. Its average was calculated for all data points for different K values and the K value with maximum silhouette validity index was selected as the optimum.Individual joints inside each group were found by grouping all the neighboring triangles and setting a threshold for the minimum number for facets. Finally, random sample consensus (RANSAC)was being used to determine the plane parameters.The orientation measurements from this approach were compared to results obtained in Riquelme et al. (2014) for a test dataset. While the absolute values of deviation for dip and dip direction were almost the same,the average error for the dip was found to be higher.Further,it took 2.5 h for automatic discontinuity extraction with almost 0.2 million points because of the iterative steps for finding initial clusters centers and the optimum number of joint sets. Joint sets extraction results using the proposed automatic clustering showed that the technique was not robust enough for rock mass data with weathering and exfoliation features. The problem of clustering using the point cloud data is that small exposures and rough surfaces are under-sampled whereas a single discontinuity plane will be over-sampled because of higher number of representative points. In addition, clustering techniques and statistical models label each point of data as part of discontinuity surface,which can result in other sections of rock mass as weathered rock or trees also to be labeled as discontinuity surface.

With increasing computing power at their disposal,researchers have started developing sophisticated techniques for joint recognition on 3D point cloud data of rock mass. Riquelme et al. (2014)proposed a semi-automatic method to estimate the joint plane equations by determining joint sets using kernel density estimation followed by the application of density-based spatial clustering of applications with noise (DBSCAN) (Ester et al., 1996) in order for finding individual joint clusters inside each joint set.An example of the extracted joint sets is shown in Fig. 5 where each set is represented by a different color.Finally,PCA was used to fit planes to each discontinuity cluster. Approximately 80% of computation time was used in the estimation of normal vector for each point using the K-nearest neighbors (KNN) search and the coplanarity test. However, using sensitivity analysis, it was shown that values for the parameters such as the number of neighbors and maximum deviation for the coplanarity test play a crucial role in discontinuity set assignment.It was found out that a greater precision of normal vectors can be obtained by considering higher number of neighbors in the KNN search. They recommended the KNN values ranging from 15 to 30 and an optimal threshold for the coplanarity test as 20%. The algorithm was tested on a dataset from the publicly available Rockbench repository(Lato et al.,2013).The performance of the algorithm was good except when the surface of the model was irregular. Finally, this algorithm was not recommended for performing analysis on large datasets(>20 million points)at once due to the difficulties in finding the dominant/principal orientations from stereo plots as well as extensive computation times.

Fig. 5. Identification of joint sets from 3D point cloud (Riquelme et al., 2014): (a) Picture of scanned road cut slope; and (b) Identified joint sets.

Zhang et al. (2018) identified discontinuity planes by a simultaneous classification of the raster grids of rock mass digital elevation model with three parameter layers including slope aspect, slope gradient, and standard deviation of elevation using the iterative self-organizing data analysis techniques algorithm(ISODATA). The final planes from classified clusters were determined by selecting points with deviation from mean elevation(DEV) values between +1 and -1. The method showed minimal differences with manual measurements.The accuracy depended on the two ISODATA algorithm parameters including the minimum number of points in cluster and radius of neighborhood window.Also,an analysis in terms of the computation time with respect to point cloud size was required.

In order to eliminate human bias which is introduced in clustering algorithms in terms of K and initial cluster locations, Kong et al. (2020) utilized the clustering by fast search and find of density peaks (CFSFDP) algorithm (Rodriguez and Laio, 2014) to automatically detect the number of clusters. This algorithm only considers the local density of points and the minimum distance between a point and another point of higher density.Sine-squared of the acute angle between normal vectors was used as a measure of the distance between two points (Jimenez-Rodriguez and Sitar,2006; Jimenez, 2008). Once the clusters were defined, DBSCAN was used for finding individual joint planes and RANSAC was used for determining plane parameters similar to Riquelme et al.(2014).The processing time for 1.5 million points and 0.5 million points was 5.5 h and 1.5 h, respectively. Majority of the time was consumed in creating the distance matrix of 3D points for the CFSFSP algorithm. The average error for this method was found to be less than that by Riquelme et al.(2014)and Chen et al.(2016)for orientation computations. This increased accuracy proved the significance of computing normals using the iterative reweighted plane fitting(IRPF)method(Wang et al.,2013)and a better cluster segmentation using CFSFDP (Gao et al., 2019).

3.1.2. Region growing-based methods

Unlike the traditional methods of using clustering techniques for joint plane segmentation,Wang et al.(2017)proposed a region growing approach for extracting the full extent of joint planes from 3D point cloud.In region growing,a seed point is selected randomly from the point cloud and then the region is expanded by adding neighboring points satisfying the preset conditions. The point normal and curvature information estimated using K-nearest neighbors and least-squares plane fitting methods are used to find and grow the seed points.The region growth and selection of new seed points were controlled using two user-specified thresholds based on angular difference between point normals. The ability to extract full extent of fracture regions and fast processing time are found to be the strengths of this method. However, the computation time steeply increases for more than 1 million points.Also,the method needs improvements in terms of eliminating outlier clusters.

To improve the computation time using region growing for joint plane extraction in case of large point clouds with high resolution,Ge et al.(2018)suggested two solutions including gridded data and modified region growing algorithm. The raw point cloud was transformed into gridded data with evenly spaced rows and columns where each point could be accessed using row and column indices. This saved data retrieval and processing time in point clouds. Next, the modified region algorithm was characterized by an efficient growth criterion that increased the probability of making more neighboring points as the seed points. The growth was controlled using a single user-specified threshold of maximum normal angle difference. Further, in this method, point normals were estimated using only four neighboring points. This method resulted in a 97.66% less computation time compared with normal region growing. The segmented plane orientations were found to be closer to manual measurements. The identification of joint planes using this method is highly dependent on the threshold parameter where values should be between zero degree and the minimum normal difference between all joint planes.

Drews et al.(2018)further improved the accuracy and precision of region growing algorithm for joint plane segmentation by specifying additional growth criteria other than normal and curvature differences, such as distance of candidate points to the points and a fitted plane of growing region as well as standard deviation of candidate points.The increased accuracy was validated with statistical significance by comparing the orientation values with the ground truth (field measurements) and values from Virtual Reality Geological Studio(VRGS)(Hodgetts et al.,2007).It was found that the actual segmentation time using region growing was only around 6%and the rest of the time was used in normal vector calculations.

Hu et al. (2019) proposed an automatic approach for detecting joint planes in 3D rock mass point clouds by determining coplanar points in a voxelized point cloud and merging individual voxels into planes by using region growing. Further processing was implemented after region growing to improve the accuracy of plane detection by using unprocessed points in the remaining steps.High accuracy and speed in detecting planar regions in point cloud were found to be the strengths of this approach.However,to determine the optimal configuration of eight parameters, a representative subset of the input point clouds needs to be selected and employed for testing. Since this initial trial-and-error procedure must be repeated for each new point cloud, it conflicts with the automatic nature of this method. Besides, there was no discussion related to the effect of the variable density in point cloud on the performance of the algorithms. In the future, it is also necessary to check the performance in terms of dip and dip directions of the detected planar regions.

3.1.3. Other methods

The earliest attempts were made to extract joints and their orientation information using digital images of rock surfaces(Franklin et al.,1988;Kemeny and Post,2003).Roncella and Forlani(2005) presented a multi-resolution RANSAC (Fischler and Bolles,1981) algorithm for extracting planar surfaces from DEMs of rock mass. It was one of the first approaches in this domain. The algorithm was slow and unstable.Also,the parameters were selected by trial-and-error. Ferrero et al. (2009) presented a graphical user interface(GUI)software,namely RockScan,that lets the user select part of the image and segment discontinuity planes by iteratively running RANSAC for the selected points. Because of the iterative nature of the algorithm,it was computationally expensive to be run for the entire point cloud, and hence that is not practical. Further,there was no discussion on the values for different extraction parameters such as the threshold for RANSAC. Such analysis is also plagued with a bias as only the features considered important by the user are investigated. Also, its success depends highly on the skill and experience of the user.

Mah et al. (2011) considered each triangular element of a 3D mesh model as a plane,plotted their dip direction and dip as poles on a stereonet,and then used an automatic pole density contouring to determine the joint sets. However, the set orientation values were less accurate when compared with manual measurements.Gigli and Casagli (2011) presented a MATLAB (MathWorks, 2020)tool,referred to as Diana,for semi-automatic extraction of joint sets and orientations from a given point cloud. Their approach was based on moving a cube through the entire point cloud and extracting least-squares fitting planes inside the cubes. This resulted in the segmentation of the point cloud in planar regions.Then,these planar surfaces were merged based on their orientations and the distance from each other, resulting in individual discontinuity planes.The ability to resize the search cube helped to extract even smaller features from point clouds with different resolutions.However,the values of parameters such as size of cube and angular and distance thresholds for planar segments merging depended on the point cloud resolution, noise and rock surface complexity. The computation time increased with a rise in the size of the point cloud. These reasons necessitate the manual collection of discontinuity parameters to complement the semi-automatic approach which makes the entire process comparable to manual field measurements in terms of time and cost.

Gomes et al. (2016) proposed a PCA-based algorithm that recursively divided the point cloud into subsets until they were planar or near-planar, as determined by user-specified thresholds.The algorithm was found to be accurate in terms of the orientation values of detected joint planes from rock mass point cloud. However, it either detected several planes or no planes on rough surfaces. Moreover, in case of rough rock faces and a low-resolution point cloud,the dip direction of detected planes could be inversed.A similar approach of recursive division of point cloud into smaller subsets(cells)of planar points is used in the FACETS plugin(Dewez et al.,2017)for CloudCompare software(CloudCompare,2020).The adjacent cells are then merged back based on the similarity of their orientation values to form complete joint planes.

Aerial photogrammetry can generate photomosaic map of rock mass slopes. Vasuki et al. (2014) presented an approach where discontinuity traces were detected from UAV images using phase congruency and phase symmetry algorithms complemented by user inputs. The third dimension of these two-dimensional (2D)features was then computed using the DEM. RANSAC was used to compute the best fitted plane to the detected 3D points whereas the outliers or noise points were eliminated using the cutoff distance from the plane.The approach showed a good performance in terms of time and accuracy of computed orientations.However,the accuracy for the fault trace detection method was 79.8%, i.e. the algorithm could not detect some fault lines represented by faint edges in the images.The user inputs helped in perfectly capturing the geometry and location of the original fault trace lines.There is a need for testing the effectiveness of this approach on different rock textures and geometries.

3.2. Persistence and trace length

Sturzenegger and Stead(2009b)determined the joints from 3D point clouds by manually fitting circular planes to individual rock mass discontinuities using the Polyworks software package(InnovMetric,2020).The diameter of the fitted circular regions was assumed to be equal to the equivalent trace length for discontinuities. Sturzenegger and Stead (2009a) also pointed out the superiority in using 3D models for discontinuity persistence estimations in case of trace lengths exceeding 5-10 m and relatively higher benches.However,Sturzenegger et al.(2011)outlined the ground resolution of the model and the orientation of exposed rock mass as the major drawbacks that affect the accurate estimation of discontinuity persistence using this method.

Many different algorithms are discussed in the previous section for the detection of planar joint surfaces.Discontinuity persistence is basically the areal extent of these surfaces (ISRM,1978). A polygon bounding the planar points for each discontinuity can be determined by applying convex hull algorithms (Preparata and Hong, 1977). Minimum and maximum persistence can be determined from the dimensions of this polygon (Gigli and Casagli,2013).

When a rock face is investigated and mapped using UAVs, the discontinuity traces can also be extracted either manually or semiautomatically from the rock images collected by the UAV’s image sensor and projected on the best-fitting plane for rock joints. The lengths of these projected lines could be used for the estimation of the persistence of discontinuities (Priest and Hudson, 1981; Reid and Harrison, 2000; Lemy and Hadjigeorgiou, 2003). Each trace is associated with a discontinuity set based on the angle between the trace and the intersection lines of rock face plane and discontinuity set plane.A similar approach was also used by Kemeny et al.(2006).The results from the 2D approach indicated inconsistencies with the ground truth which could be attributed to the biased estimate of persistence for longer traces,practical difficulties during the field survey, or inaccuracies in fitted discontinuity set plane.

Some limitations of 2D approaches for a complete detection of the traces include the lack of points at the intersection of discontinuity planes and rock mass surfaces, division of a single trace into a number of broken fragments, and the generation of redundant segments of traces due to irregular rock surfaces (Li et al., 2016). Zhang et al. (2019) proposed to extract the trace lines from the 2D image of the rock face and then link the trace pixels with its corresponding points in a 3D point cloud. Linking pixels with point cloud data was completed using coordinate system conversion,and spatial trace coordination was computed using interpolation in triangulated point cloud data.The full trace length was equal to the Euclidean distance between the endpoints of the trace, and dip and dip direction could be computed by fitting a plane to trace points. The process of extracting trace lines from images is affected by occlusions, the position of the sun, shadows,weather conditions,rock type,color,and light conditions(Reid and Harrison, 2000).

Umili et al. (2013) presented a semi-automatic approach for extracting the traces from the digital surface model (DSM) of the rock surfaces. The idea was to calculate the minimum and maximum principal curvatures at each vertex.If the absolute value of any of these curvatures was greater than a preset threshold for a vertex,then the vertex belonged to the convex or concave edges of a discontinuity. The vertices were then connected to create edge paths which were further segmented into edges and segments using the RANSAC.Finally,the segments were clustered into traces using the ISODATA algorithm(Ball and Hall,1965).The mean trace length was calculated using either a circular window (Zhang and Einstein, 1998) or a circular scanline (Mauldon et al., 2001) sampling with varying radius.The time needed for trace detection using this method was similar to manual extraction from an orthophotograph.The parameters of the ISODATA algorithms,such as the minimum number of members in each cluster,the maximum variance, and the minimum pairwise distance, are needed to be pre-specified. Furthermore, a sensitivity analysis of the curvature threshold values is essential to be performed to determine the range of optimal values.

Cao et al. (2017) identified edges of triangular elements in rock mass mesh as discontinuity traces based on the angle of intersection of corresponding triangular units. An edge was selected as a part of the trace if the corresponding intersecting angle was larger than a user-specified threshold. The resulting traces were postprocessed to eliminate noises and redundancies. This is a simple method with a reasonable accuracy to automatically identify the discontinuity traces.The output of this method is dependent on the angular threshold value, mesh quality, and degree of weathering.

Li et al. (2019) presented an automatic method of extracting discontinuity traces from a 3D mesh model of rock mass face. It involved the detection and labeling of trace vertices as feature points using normal tensor voting (Kim et al., 2009) and userdefined thresholds (Wang et al., 2012). The detected feature points were divided into groups with each group composed of adjacent points based on a common edge and difference of angle between normal and threshold. After this, trace segments which consisted of a continuous chain of feature points were estimated using a trace growth algorithm. This resulted in a number of trace segments that belonged to a single discontinuity trace. The segments belonging to one trace were connected using a similar growth algorithm but with different threshold values.Finally,each trace was made smooth and continuous by removing redundant trace segments through comparing their direction with the principal direction of the trace. The identified traces are depicted in Fig. 6. This method is more robust for noisy point cloud data and artificial edges in the mesh induced by blasting.The accuracy of the output depends on the size of the mesh triangular element and the optimal values of the parameter. However, no evidence is given regarding the accuracy and running time of the presented algorithms.

Fig. 6. Discontinuity trace extraction (modified after Li et al., 2016): (a) Picture of scanned road cut slope; and (b) Identified discontinuity traces.

Guo et al. (2018) proposed a curvature-based semi-automatic methodology for discontinuity trace extraction directly from 3D point clouds. In this method, normal vector for each point was calculated using PCA and later adjusted so that all the normal vectors point towards the same direction. Then, curvature information was calculated for each point based on one-dimensional(1D) truncated Fourier series. Potential trace points were selected based on user-specified threshold for curvature. These potential points were further thinned through a curvature-weighted Laplacian smoothing technique. The thinned traced points were then linked to form final trace segments using a weighted line growing algorithm. The method resulted in more detailed and fast trace segment extraction from 3D point clouds as compared with the Compass plugin (Thiele et al., 2017) in CloudCompare and the previously discussed method proposed by Li et al.(2019).However,the method could not detect traces which intersect planar surfaces of rocks and differentiate between artificially induced traces (e.g.due to blasting)and natural traces.Later,Guo et al.(2019)proposed an automatic method for detecting discontinuity traces that used geometry as well as texture information from 3D points of rock mass. The texture and normal maps (2D) were generated from 3D point cloud by converting it into a mesh and then automatically unwrapping it using the Blender software. The texture map contained the RGB values of points,and the normal map included the normal vectors of points mapped to a 0-255 range. An edge detection technique, referred to as the multi-scale edge detector(MSEdge, 2017), was utilized to separately detect traces from the normal and texture maps.The traces from both maps were merged in order to obtain the final extracted traces, which were mapped back to the corresponding 3D points. The method was effective in detecting traces on smooth surfaces of rocks. The addition of texture information in trace detection could also cause interference due to shadows or other noises which need to be eliminated separately.

Bolkas et al.(2018)further explored the application of 2D image edge detection techniques such as the space-frequency transforms for trace detection from LiDAR data. They converted the 3D model into a 2D greyscale image by mapping the third dimension to a grey-scaled color. Such a conversion might cause loss of information from certain sub-horizontal or sub-vertical parts of rocks.The surface of 3D model was decomposed using wavelet function that gave multi-scale information of edges. The performance of contourlet (Do and Vetterli, 2005) and shearlet (Labate et al., 2005)transforms in automatic trace detection was found to be superior than other edge detection method. Also, the multi-scale feature approach helped to reduce noises from the data. The results were solely based on a 10-m long section of entire 3D model. Further investigation needs to be conducted using larger point cloud datasets from different rock types. It should also be noted that in this research,transform parameters were determined using a trialand-error approach.

Riquelme et al.(2018)proposed a method for a semi-automatic extraction of the discontinuity persistence directly from a 3D point cloud. Initially, the point cloud of a rock mass was classified into discontinuity sets and clusters using an open-source software called the Discontinuity Set Extractor.Then,coplanar clusters were identified and merged into a single cluster. The points of each discontinuity set were extracted, and a coordinate system transformation based on the dip and dip direction of the parent discontinuity set was applied. Once this transformation was performed,the persistence in the dip and dip direction,the maximum persistence,and the area of persistence from the convex hull were estimated.The accuracy of this method depends on the correctness of the discontinuity set extraction from point cloud which is affected by the presence of noise,vegetation,or soil.In addition,the parameter K which controls the sensitivity of coplanarity test could also increase or decrease the measured persistence.

3.3. Spacing

According to ISRM (1978), the spacing has been defined as the perpendicular distance between two discontinuities which are adjacent to each other.There are mainly two approaches proposed in the literature for determining the spacing of discontinuities from 3D models of rock slopes. The first approach considers the predetermined joint plane equations as the input. When the equations of the discontinuity surfaces are available for the discontinuity set,spacing can be derived by analyzing them in a 3D space.For each discontinuity set, the discontinuities are mostly parallel.Therefore, every discontinuity in the set is assigned the mean orientation of that set which makes them perfectly parallel to each other.Then,the spacing is calculated as the perpendicular distance between two adjacent discontinuities (Riquelme et al., 2015;Wichmann et al., 2019; Kong et al., 2020). Another proposed method in the same category is the use of a virtual cylinder of which base is a discontinuity plane as shown in Fig. 7. All the discontinuity polygons which are intersected by the cylinder belong to the same set and the distance between these intersection points is used to calculate the mean,minimum,and maximum joint spacings (Gigli and Casagli, 2011). This approach showed a good accuracy;however, it should be tested on different rock types.

In the second approach,the discontinuity traces projected in the 3D space are considered as the input.A clustering algorithm such as the K-means clustering is utilized to divide the projected traces into K groups. Then, a virtual scanline is created perpendicular to the average orientation of traces in each group,as shown in Fig.8.The average spacing is calculated for the set by taking into account the average lengths of line segments which are formed by an intersection between the scanline and the discontinuity traces(Li et al.,2019).

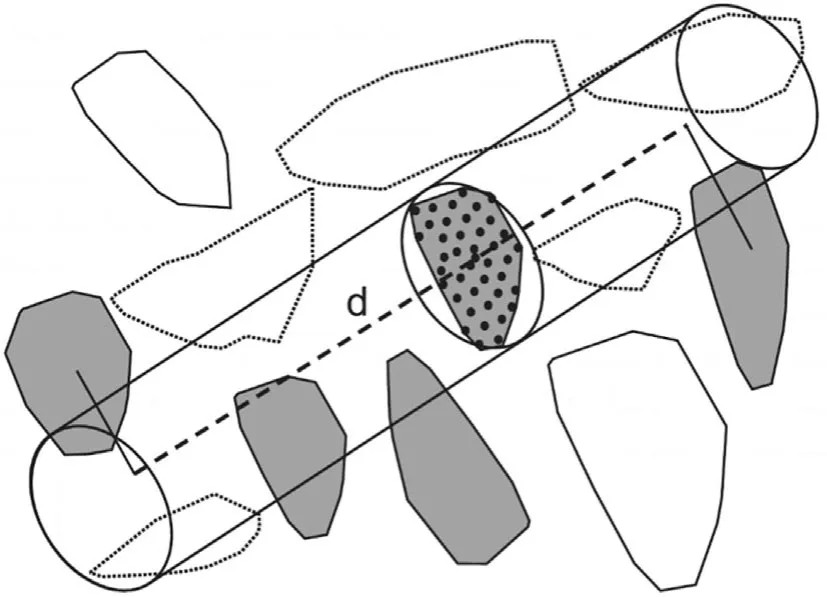
Fig. 7. Virtual cylinder for spacing calculation (modified after Gigli and Casagli, 2011).

Fig. 8. Virtual scanline plot perpendicular to extracted traces (modified after Li et al., 2019).

3.4. Roughness

The roughness of a discontinuity is defined as the measure of irregularity and waviness of its surface relative to its best-fitted plane (ISRM,1978). It plays a significant role in defining the shear strength of discontinuities and mechanical behavior of rock mass(Patton,1966;Barton,1973,1976;Zare Naghadehi,2015;Zare et al.,2008). It can be measured from the point cloud of rock mass collected using a Laser scanner or photogrammetric methods.However, this way of measurement is affected by the presence of noise in data. Sturzenegger and Stead (2009a) presented two methods for quantifying roughness based on linear profiling,compass and disc-clinometer as suggested by ISRM (1978). In the linear profiling method,the roughness is represented by a heat map depicting normal distance between the discontinuity surface and fitted plane. In the other method, square windows are created at random locations on the discontinuity surface, and then the orientation of the plane fitted to points inside each window is computed. The average orientation of these windows is represented as the roughness angle for the given discontinuity. These methods were implemented by Henk and Laux (2015) to automatically extract 2D and 3D roughness values of a given discontinuity from laser scanner data of an outcrop.The fitting of planes to the gridded points can be achieved using either the ordinary leastsquares (OLS) regression (Fardin et al., 2004) or the orthogonal distance regression(Pollyea and Fairley,2011)methods.In the case of noisy data, these methods might cause overestimation of the roughness values. The methods use meshing for creating linear profiles and hence depend on the characteristics of triangulation.

When the snake reached the palace, all the courtiers shook and trembled with fear down to the very scullion, and the King and Queen were in such a state of nervous collapse18 that they hid themselves in a far-away turret19

Another approach involves creating cross-sections on the surface of 3D models of rock mass and comparing them to Barton’s standard joint roughness coefficient (JRC) profiles (Barton and Choubey, 1977) to automatically estimate the coefficient for individual discontinuity set. The visual inspection is difficult and introduces a bias in the process. JRC can also be calculated using an equation developed by Tse and Cruden (1979):

where Z2is the root mean square (Myers,1962) of the first derivative of discontinuity profile which is given by

where （xi， zi） and （xi+1， zi+1） are the coordinates of consecutive points on the profile with Δx as the interval between them,N is the total number of points, and Lnis the considered profile length.

The profiles are created by intersecting a discontinuity surface with planes parallel to dip direction and perpendicular to it (Li et al., 2019). Haneberg (2007), on the other hand, used empirical equations developed by Maerz et al. (1990) for JRC and asperity angle i (Patton,1966) estimation, as stated by

where c is an empirical constant; and Rpis a roughness profile index,defined as the ratio of the true length of profile surface to the projected length along the best-fit plane, given by

where Δs is the distance spacing between points.

It has also been found that there is no significant difference between the values of JRC computed using the above equations.However, the roughness measured using these methods is limited by the resolution of point cloud and accuracy of 3D coordinates.It was found that the roughness calculated from the triangulated surface of the discontinuity (generated from a 3D point cloud of a terrestrial laser scanner)using the empirical roughness parameter developed by Grasselli et al.(2002)was more robust to noise than other roughness measures (Bitenc et al., 2015). Bitenc et al. (2019)proposed surface and range denoising methods for reducing the effect of noise and improving the estimated roughness values.The JRC is popular among engineers and researchers all over the world in the field of rock mechanics. Yong et al. (2018) proposed a nonvisual method for comparing discontinuity linear profiles with Barton’s standard profile.It involved representing the standard JRC and rock profiles into feature vectors based on the distribution of angular variation of the profiles. The comparison between two feature vectors was performed using the vector similarity measures(VSM)such as Dice(Ye,2012),Jaccard(Dharavath and Singh,2016),and Cosine(Ye,2015).The VSM-based JRC values were found to be in agreement with traditionally computed ones. However, the applicability of this method to a 3D discontinuity surface acquired using a laser scanner or photogrammetry is yet to be evaluated.Oppikofer et al. (2011) presented a method of calculating the JRC using the amplitude of the asperities along with the profile of the discontinuity surface. The equation is given as (Barton,1982):

The JRC values estimated using this method are similar to those evaluated using visual comparison with Barton’s standard profiles in case of a TLS-acquired rock mass point cloud.

The roughness of a discontinuity can also be measured by estimating the roughness angle of its surface. After the extraction of joint surfaces from the 3D point cloud,a sliding cube with varying dimensions can be moved on the surface. If the points inside the cube are more than the user-specified threshold,then a best-fitting plane is computed. The orientation value of the plane gives the discontinuity roughness angle for various cube sizes (Gigli and Casagli, 2011). The roughness angle decreases as the size of the cube increases showing the scale dependence of it. Ünlüsoy and Süzen (2019) proposed a new method of calculating JRC values of discontinuity surface profiles generated using a TLS scanner through comparing the area difference between the plot of power spectral density (PSD) functions of sample surface profiles with each of Barton’s ten template profiles. The JRC range with the minimum area difference was primarily selected. An interpolation algorithm for computing the quantitative value of JRC was also proposed. This approach was found to be more accurate and reliable than the JRC estimations using conventional Z2formulae proposed by Tse and Cruden(1979),Tatone and Grasselli(2013)and Jang et al. (2014).

Cai et al. (2018) proposed another quantitative estimate of roughness called the index of roughness (IR) which was more closely linked to the shear strength of discontinuities. This parameter was found to be relatively better in correlation with JRC than Z2and Graselli’s method. Ge et al. (2015) proposed an index called brightness area percentage (BAP) to estimate the surface roughness of rock using its digital terrain model created from a TLS point cloud. It was basically defined as the percentage of bright triangles in the joint surface when light was irradiated using a virtual light source. The degree of brightness of tiny planes was directly related to their orientation(dip and dip direction)which is,in turn, related to their resistance during shear failure. This index was found to be capable of characterizing the anisotropy, scale effect, and interval effect features of roughness similar to fractal dimension(D)and Graselli’s method.This method also requires the non-stationary component of the roughness to be removed before estimating the BAP.

Fardin et al. (2004) calculated the fractal dimensions, D and A,from the point cloud of the in situ laser scanner using the roughness-length method (Malinverno, 1990). They presented a fast way of calculating primary roughness which governs the stability in high stressed fractured rock masses from a 3D point cloud.However, due to the limitations of scanning resolutions and the presence of noise, it was not capable of calculating the secondary roughness.

The 2D (Zhang et al., 2014a) and 3D (Zhang et al., 2017a) JRCs were also proposed to estimate the roughness of discontinuity profiles collected using a laser scanner.Hong et al.(2006)used the specific roughness coefficient proposed by Belem et al. (2000) to estimate 3D roughness from the point cloud of rock surface. Also,Lai et al. (2014) used three curvature-based roughness measures,i.e. curvature difference, curvature sampling, and curvature ratios,mainly by exploring the use of curvature-based indices to estimate roughness from 3D mesh models of rock mass. The relationship between the shear resistance and these indices is not evident yet.Mostly, these indices were utilized for differentiating between planar and rough regions such as discontinuities, fractures, and bedding planes in a fast and efficient way.

3.5. Block size

The block size distribution of a rock mass is usually estimated by creating a 3D discontinuity model using rock mass characteristics such as joint orientation, spacing, persistence, and others (Jafari et al., 2013), which is a statistical approach. As discussed in Sections 3.1-3.4,there are various algorithms available to extract these required parameters from 3D point clouds. These extracted parameters can be used for estimating block distributions in a rock mass point cloud.Mavrouli et al.(2015)estimated in situ block size distribution using the following formula:

where vbis the block volume (m3), and siis the spacing value for intersecting joints.

Similarly,Wichmann et al.(2019)also computed block size from 3D point cloud data using a formula given by Cai et al. (2004):

where αijis the acute angle between two joint set normals.

However,these equations result in an underestimation of actual block sizes due to their simplified approach. Chen et al. (2017)presented an algorithm for automatic extraction of block size directly from the 3D rock mass point clouds generated by laser scanner or photogrammetry,as shown in Fig.9.The algorithm used joint planes extracted using the RANSAC shape detector (RSD)plugin developed by Schnabel et al. (2007), available in the Cloud Compare software. The outlines for the extracted planes were estimated using the concave hull algorithm (Rosen et al., 2014).Intersecting lines between non-parallel planes were found using geometrical equations.Two pairs of intersecting planes that share a common plane were used as an identification of the blocks. The final blocks were selected by using a combination of the Floodfill algorithm (Nosal, 2008) and the volumetric method. The blocks were assumed to be in the shape of symmetric parallelepipeds and their sizes were calculated from the volume of the tetrahedron formed by intersecting segments. Minimal deviations were found on comparing the results for this method with manual measurements using the Cloud Compare software. This method is applicable only to the exposed part of the blocks of a rock face.Some of the challenges to this method are irregular rock surfaces and complex shapes of blocks.

Fig. 9. Block detection from a 3D point cloud (Chen et al., 2017).

Fig. 10. Percent-wise share of different 3D models used for discontinuity characterization.

4. Discussion

This paper presents a critical review of methodologies and algorithms in the literature for the automatic extraction of discontinuity characteristics including the joint set number, joint plane orientation,trace length,persistence,spacing,roughness,and block size, utilizing 3D models of the rock mass. The most popular 3D models used in the literature are point clouds and triangular meshes as shown in Fig. 10. As there are numerous different approaches presented for each discontinuity characteristic, it is important to understand and analyze them to find some of the best methods in case of each characteristic.Therefore,in this paper,the methods have been categorized based on five parameters including joint sets and orientation, joint persistence, spacing, roughness,and block size. Each section contains a summary of the major studies conducted for automatic acquisition of those parameters.This review provides a comprehensive list of all the research conducted on this topic, which aims to help researchers find any possibility of improvement in the currently presented methods and direct future research. This survey is also important from the viewpoint of developing an automated rockfall risk analysis system similar to what performed by Riquelme et al. (2016). There are empirical indices for rockfall hazard in slopes such as CRHRS(Santi et al., 2008) and ROFRAQ (Alejano et al., 2008), which could be computed remotely given that the discontinuity parameters are automatically extracted from the point cloud data of the slope.

Table 3 summarizes the strengths and drawbacks of each method presented for discontinuity parameter extraction. This table indicates that the clustering-based and region growing-based methods are popular for the computation of joint sets and orientations. It also highlights the major challenges in the extraction of discontinuity parameters from the different 3D models.In the case of“joint set number and plane computation”,the major challenges are higher computation times for clustering-based methods, and increased number of parameters and inaccurate joint boundary detection for region growing-based methods. As for the “trace length or persistence”, the curvature-based methods are found to be accurate and fast for discontinuity trace detections in rock mass point cloud or triangular meshes. These methods, supplemented with texture information, are demonstrated to detect traces in smooth rock surfaces as well. A major challenge identified in this approach is the error due to the presence of noise or bad lighting conditions which is introduced with the texture information. One of the ways of tackling this problem is to pre-process the texture information to eliminate the presence of noise with the application of state-of-the-art shadow and weather effects removing algorithms.A review of various image enhancement and de-weathering techniques for outdoor images has been presented in Wahab et al.(2013). The selection of a method depends on the nature of noise such as fog, haze or rain.

The main factors which influence the application of these techniques in a real mine environment can be summarized as accuracy, number of parameters, running time, and robustness. The joint plane extraction is the first task in an automatic feature extraction effort.The analysis in Section 3.1 suggests that there is a trade-off between running time and number of parameters in the selection of a method for extracting joint planes from rock mass point cloud data. The region growing approach suggested by Hu et al. (2019) is fast and efficient in segmenting joints but it requires the determination of optimal values for a large number of parameters.On the other hand,if the running time is not an issue,then joint set extraction using the CFSFDP and RANSAC, as presented by Kong et al. (2020), is the most appropriate method. It eliminates the human bias factor and automatically computes the number of joint sets and joint planes. In the case of a triangular mesh, K-means clustering with silhouette validity index proposed by Li et al. (2019) can be used.

If the joint planes are already extracted, the minimum and maximum persistence along dip and dip direction can be automatically computed using the convex hull algorithm, as presented by Riquelme et al. (2018). The normal tensor voting with trace growth algorithm,discussed by Li et al.(2019),is found to be more robust in trace length computation from triangular meshes. In the case of 3D point clouds, the curvature-based method of Guo et al.(2018) is effective in terms of processing time and accuracy. If the rock surface is relatively smoother, then the multiscale edge chain detection method (Guo et al., 2019) which extracts traces from point cloud data based on texture and geometrical information is recommended.

The spacing can be calculated as the perpendicular distance between joints from the joint plane equations (Riquelme et al.,2015; Kong et al., 2020). In the case of a mesh, it can be determined using a virtual scanline and K-means clustering method

where the value of K is equal to the number of joint sets detected in the first step(Li et al.,2019).As shown in Table 3(the“roughness”row), a number of different approaches have been proposed to quantify the 2D and 3D roughness values from point clouds,mesh,DEM, and images on both laboratory and large rock mass scales.However, few researchers have managed to integrate these methods into an automated process like what presented by Li et al.(2019). There is a need to develop novel algorithms to incorporate these roughness quantifications for automated characterization of discontinuity roughness. Another important point to note is that parameters such as spacing or roughness are usually not validated since their manual measurement involves significant errors leading to a lack of reliable ground truth data (Li et al., 2019).

Even though the computation time for block size using the joint planes intersection approach of Chen et al. (2017) is higher, it is currently the only method that directly computes the block size from the point cloud. There seems to be no algorithm available to approximate block size from triangular meshes. However, Eqs. (7)and (8) can also be used with the spacing data calculated from a mesh.This shows that there is a need to develop faster algorithms for computing block sizes directly from the point cloud or mesh models.

The point cloud data resolution collected by laser scanners or aerial photogrammetry is currently on the scale of few millimeters.Given the size of open pit mines, any point cloud collected from a slope or highwall would include billions of points. The algorithms presented in the literature have high running times when the size of the point clouds is over one million. Given the significance of point clouds in discontinuity characterization(Fig.10)in the future,it is imperative to develop algorithms that can process large point clouds in reasonable times. This can be achieved by working towards algorithms that employ parallel computing to exploit the power of GPUs or by using machine learning (Lary et al., 2016).Determining the optimal parameters for algorithms in each case requires significant time and expertise.In some cases,it is possible that the time saved from not indulging in manual measurement is used in finding optimal parameters for the algorithms which render the computational algorithms insignificant.

The presence of noises such as vegetation and debris is an important challenge in the automated processing of 3D models of the rock mass. Many applications require a pre-processed point cloud which is free of vegetation, parts of the sky, or other noises.Recent developments in the field of artificial intelligence such as machine learning and deep learning can be used for solving these problems. Weidner et al. (2019) proposed a Random Forest machine learning approach for automatic classification of TLS data into vegetation, talus, bedrock or other categories. Qi et al. (2017)showed that a 3D point cloud-based deep learning model can be employed for predicting the normals of points based on their neighboring points. Soilán et al. (2019) also used a deep learning network called the PointNet for automatic classification of an aerial point cloud collected using an ALS into vegetation,roads and other structures with 87% of accuracy. Similarly, Battulwar et al. (2020a)proposed a methodology for the application of the PointNet and DBSCAN for automated extraction of joint orientations in aerial photogrammetry-generated rock surfaces.This approach is shown to be better compared to Discontinuity Set Extractor (Riquelme et al., 2014) in terms of accuracy and time complexity for large point clouds.

5. Conclusions

Automatic or semi-automatic extraction of discontinuity parameters from the 3D models of rock mass has been a focus for researchers in the past two decades. This paper categorizes all the major previous studies in this domain based on five parameters including joint set and orientation, joint persistence, spacing,roughness, and block size. For each parameter, the presented algorithms are briefly summarized, and their strengths and drawbacks are analyzed.This is a first comprehensive review presented on this topic. The possibilities of improvement in the existing methods have been identified, which will help the engineering geology and rock mechanics communities direct future research in optimal ways.Some of the most suitable methods for discontinuity characteristics have been highlighted and recommended as follows: the region growing approach for joint set orientation, the convex hull algorithm for joint persistence, the joint plane equations for spacing, and the joint plane intersection approach for roughness and block size estimation. The overall challenges in developing an automated methodology for discontinuity characterization have also been discussed. The voxel-based region growing approach has been found to outperform conventional statistical analysis-based methods for joint plane estimation in terms of computation time,though it needs to be explored further.Other discontinuity parameters such as wall strength, aperture,filling, and seepage have not been considered in this review.Remote measurement techniques of discontinuities should also be further developed by using different sensors such as thermal(Vivas et al., 2015) or hyperspectral imaging (Kurz et al., 2011).

Furthermore, this review is limited to the measurement of discontinuity characteristics exposed on the surface of the rock mass. A complete 3D measurement of parameters such as persistence can only be achieved by undertaking subsurface investigations (e.g. using ground-penetrating radar (GPR) surveys;see Longoni et al.(2012),where the discontinuity planes extracted using GPR could be used to construct the actual model of the rock mass). The application of newly developed 3D point cloud-based deep learning models such as PointNet and PointNet++ needs to be explored for joint characterization from 3D models. These techniques can be utilized for tasks such as the classification of joint surfaces in 3D rock mass point clouds.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work has been funded by the U.S. National Institute for Occupational Safety and Health (NIOSH) under the Contract No.

75D30119C06044. We are grateful to the funding agency for their support.