基于T-S模糊故障树的制动系统可靠性分析

周亚辉， 齐金平，2，3， 李少雄， 王 康（.兰州交通大学机电技术研究所，兰州730070；2.甘肃省物流及运输装备信息化工程技术研究中心，兰州730070；3.甘肃省物流与运输装备行业技术中心，甘肃兰州730070）

importance

0 引 言

目前，中国高铁总里程已达3.5万km，占世界总里程的70%左右，运营规模庞大，且正处于从大规模建设阶段向全面运维维护阶段转变。随着动车组服役时间的增长与性能的退化，高速铁路的运营安全及维修压力将逐步凸显，对其进行可靠性分析性的必要也进而提升。制动系统是动车组的主要系统之一，主要由电制动和空气制动两大部分组成［1］，电制动是将牵引电机职能转换成发电机来完成制动，而空气制动是将相应的电信号转换成空气信号，从而输出空气施加实现功能。虽然制动系统可靠性相对较高，但是由于其结构复杂，运营环境多变，也经常出现一些故障，一旦某一环节故障导致制动失效，整车的安全性将被危及，甚至出现重大事故，因此，有必要对制动系统进行可靠性分析评估，消除潜在隐患，保证其安全运行。

故障树分析法（FTA）是可靠性研究常用方法之一，传统的基于布尔代数和概率论的故障树分析方法［2］，已经广泛使用，但其故障概率精确已知、逻辑门之间必须联系明确等条件限制了其在可靠性分析以及故障诊断中的应用。Tanaka等［3］对模糊理论首次引用到FTA中，使用模糊乘法代替了传统的逻辑运算，使其更加简单，且符合实际，但仍属于与或逻辑运算。Lin等［4］用以事件的｛0，1｝逻辑表表示事件之间的联系，模糊门得以形成，但故障程度不同，后果不同，传统的｛0，1｝已经不能满足问题分析。宋华等［5］首次提出T-S模糊故障树，使得故障概率的不确定性得以解决，但不利于专家知识和操作经验的融入。

本文结合动车组制动系统，以模糊数描述故障程度，以模糊可能性表达零部件故障率，构建T-S模糊门，既考虑到故障程度对系统的影响，也解决了事件之间的不确定性问题。同时，引入基于信心指数的专家经验，解决故障数据的缺失和多源异构问题。最后，对导致故障发生的基本事件进行重要度计算和分析，为制动系统的维修和设计改造提供参考。

1 T-S模糊故障树

1.1 事件描述

系统中零部件故障的历史数据是计算故障率的基础，对于数据的不确定性属性，结合模糊数学描述故障程度即可。若将隶属函数描述为四边形隶属函数［6］，表示为

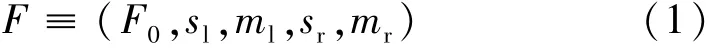
式中：F0是模糊数支撑集中心；sl和sr是支撑半径；ml和mr是模糊区。

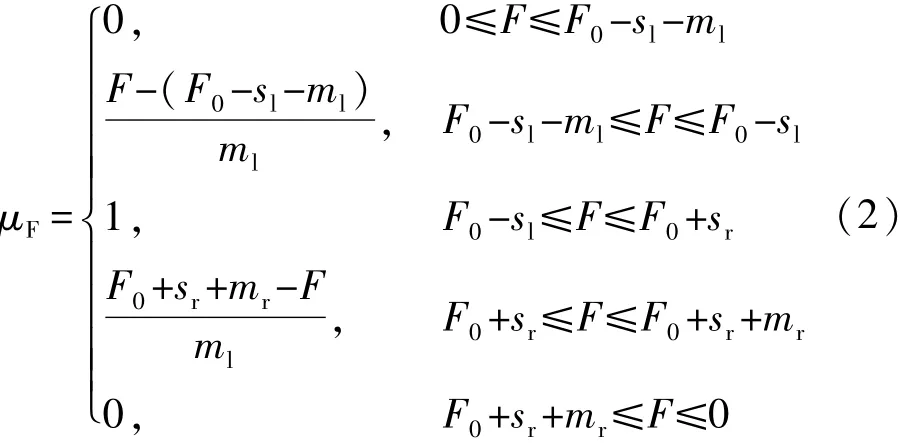
模糊数的隶属函数如图1所示。由图1可得：当sl＝sr＝0时，四边形隶属函数变成三角函数；sl＝sr＝ml＝mr＝0时，模糊数变成确定数。部件的故障程度在0～1之间取值，本文用模糊数0、0.5、1.0来描述，一般情况下，sl＝sr，ml＝mr。

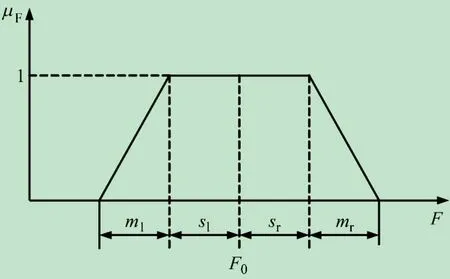
图1 模糊数的隶属函数

1.2 T-S模糊门

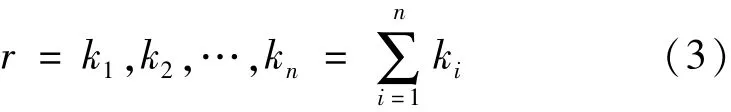
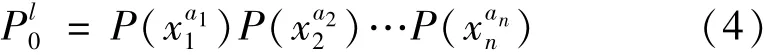
因而，得y（中间事件）的模糊可能性为：

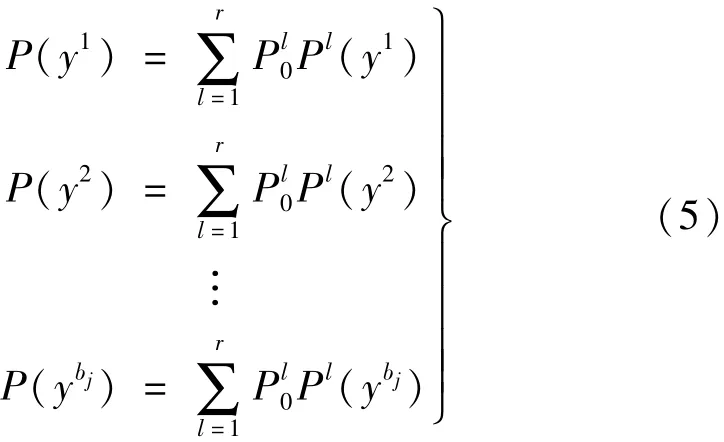
若已得基本事件x1～xn的故障状态，则上级事件出现故障的可能性为

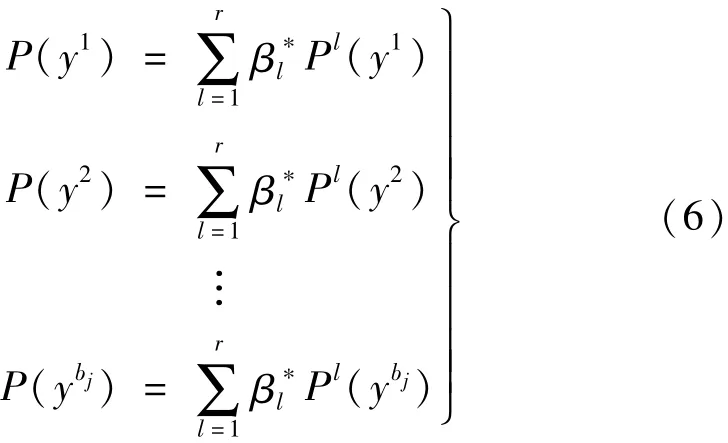
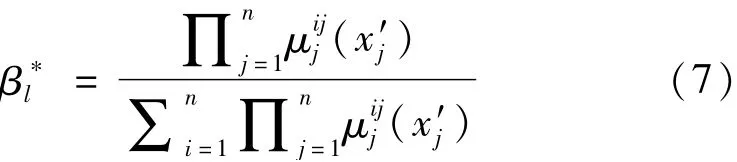
重要度作为可靠性分析的重要参数之一，反映的是最小割集故障时对系统发生故障的概率贡献［9］，是系统零部件的可靠性参数以及结构函数，应用广泛，表述如下：

若已知部件xj在故障状态为时的失效可能模糊子集为，隶属函数μp~x iij，对顶事件T为Tq的T-S模糊重要度为

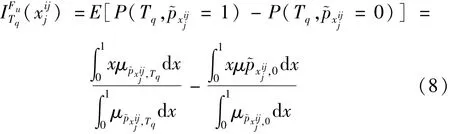
部件xj对顶事件T为Tq的T-S概率重要度为

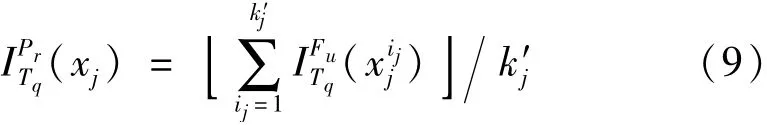
式中，k′j表示第j个非零事件故障状态的个数。

2 制动系统可靠性分析

本文以动车组制动系统中故障频次较高的部件为主，建立模糊故障树如图2所示。各事件代号含义如表1所示。

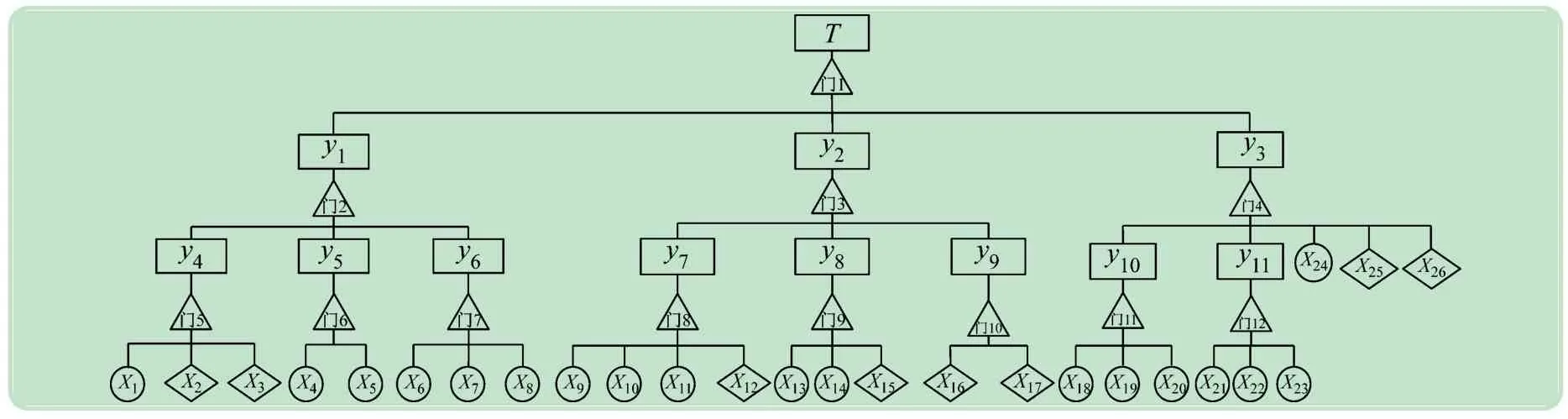
images/BZ_32_435_1145_2043_1607.png

表1 事件代码表

根据故障情况，设制动系统T-S模糊故障树事件x1～x6，x21～x24和y4，y5，y11存在（0，1）两种故障状态，隶属函数sl＝sr＝0.25，ml＝mr＝0.5，x7～x20，x25，x26和y1～y3，y6～y10存在（0，0.5，1）3种故障状态，隶属函数sl＝sr＝0.1，ml＝mr＝0.3。依据历史故障数据以及专家经验，得部分T-S模糊门如表2～4所示。

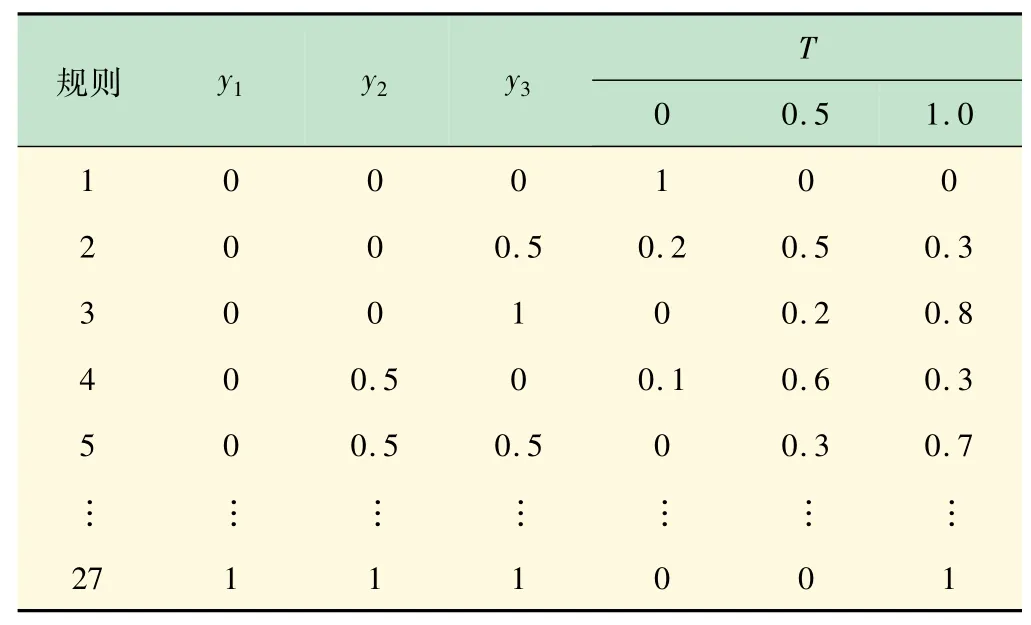
表2 T-S模糊门1

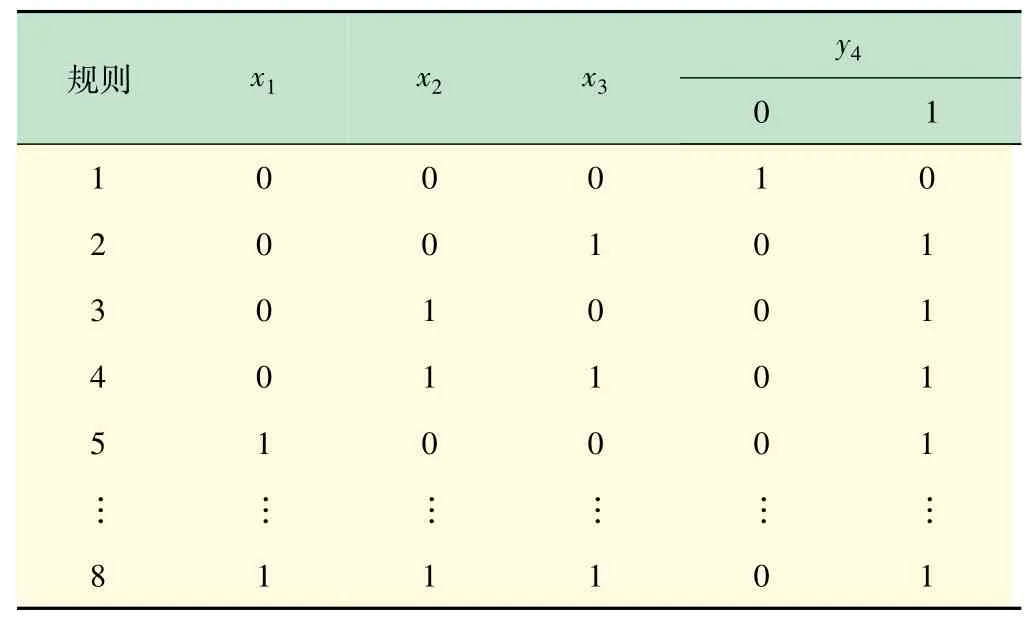
表4 T-S模糊门5

基于动车组运行统计数据以及信心指数修正的专家调查法［10-13］，可得表5中各部件故障率。假设故障程度为0.5的故障率与故障程度为1时的相等［14-17］。

2.1 已知部件故障模糊可能性，计算系统故障的模糊可能性

依据表5与式（4）、（5），可得到中间事件的模糊可能性如下：

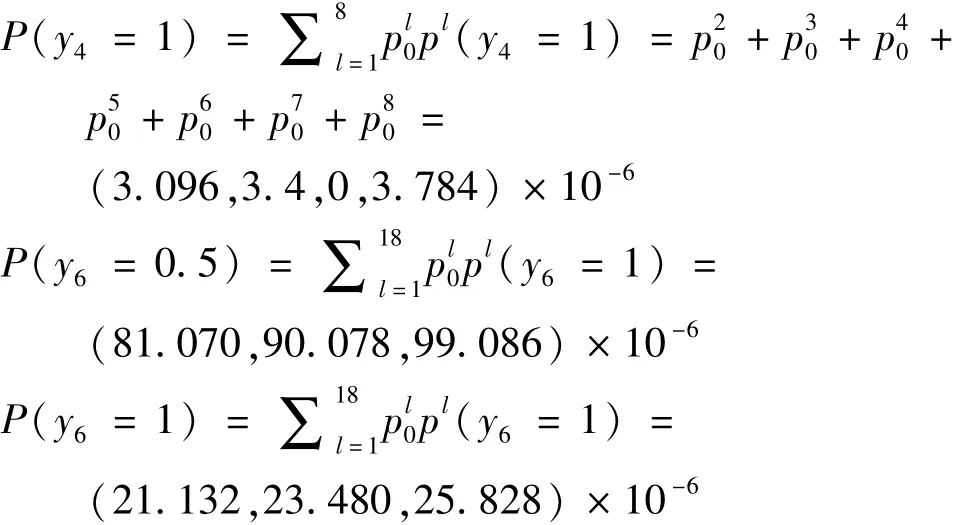
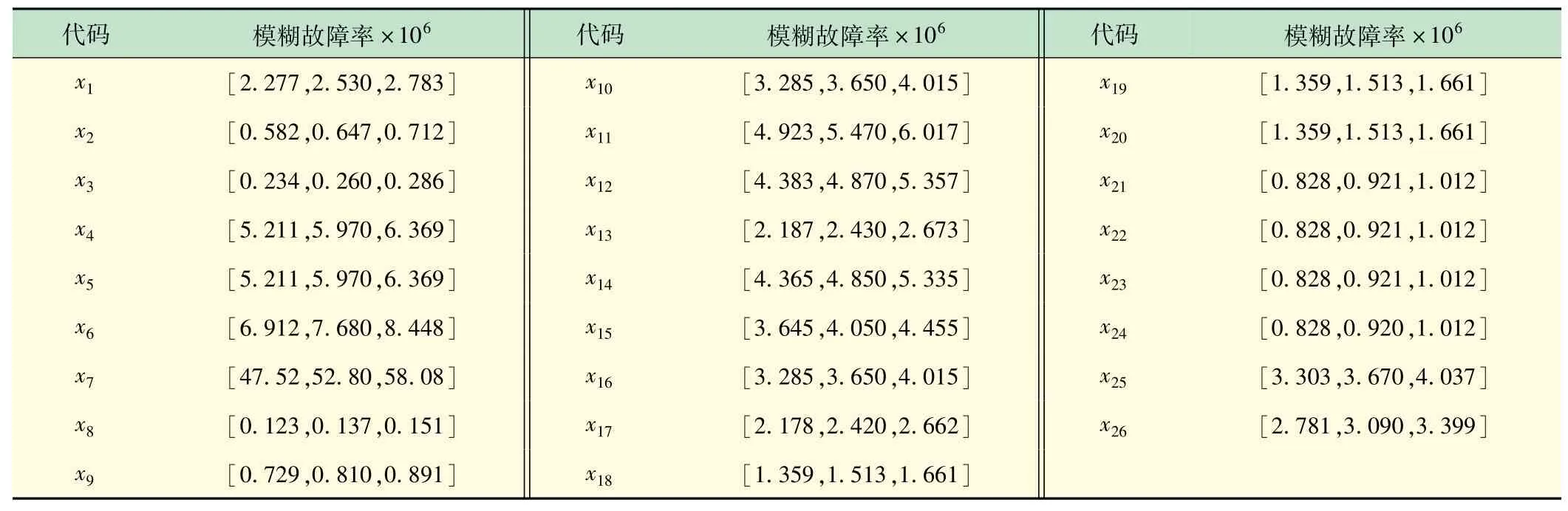
表5 制动系统各基本事件的模糊故障率

同理，计算出其他事件的模糊可能性如表6所示。

表6 中间事件模糊可能性

计算得顶事件T的模糊可能性为：

由结果可知，制动系统故障的模糊可能性与各个部件的模糊可能性为同一数量级，且电磁阀、滑行检测单元、制动盘等部件发生故障的模糊可能性远小于TS模糊故障树中顶事件发生故障的模糊可能性，与实际一致。

2.2 已知部件故障状态，计算系统故障的模糊可能性

假设部件的故障状态分别为：x1～x6＝0，x7＝0.4，x8＝0.1，x9＝0.1，x10＝0.2，x11＝0.3，x12＝0.3，x13＝0.2，x14＝0.3，x15＝0.3，x16＝0.2，x17＝0.2，x18＝0.1，x19＝0.1，x20＝0.1，x1～x6＝0，x25＝0.2，x26＝0.2。根据式（6）、（7）可得：

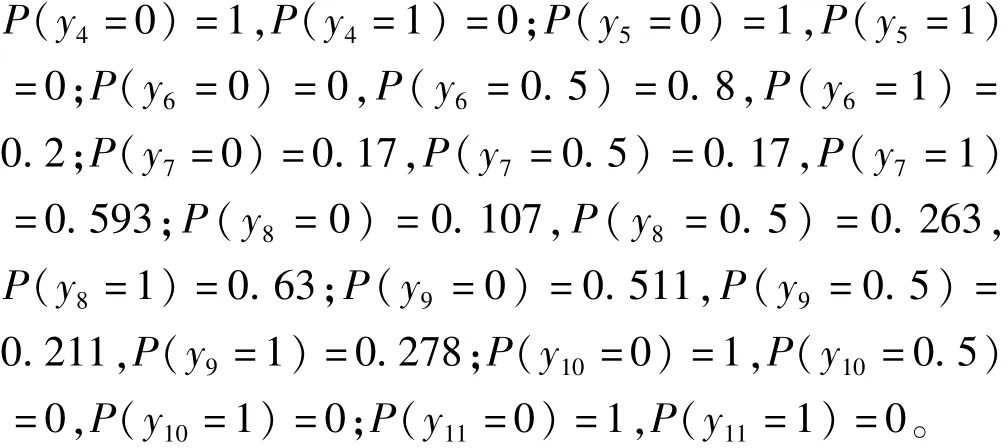
用式（4）、（5）计算y1，y2，y3，则根据表3、4可得：P（y1＝0）＝0，P（y1＝0.5）＝0.8，P（y1＝1）＝0.2；P（y2＝0）＝0.015 6，P（y2＝0.5）＝0.037 9，P（y2＝1）＝0.946 5。

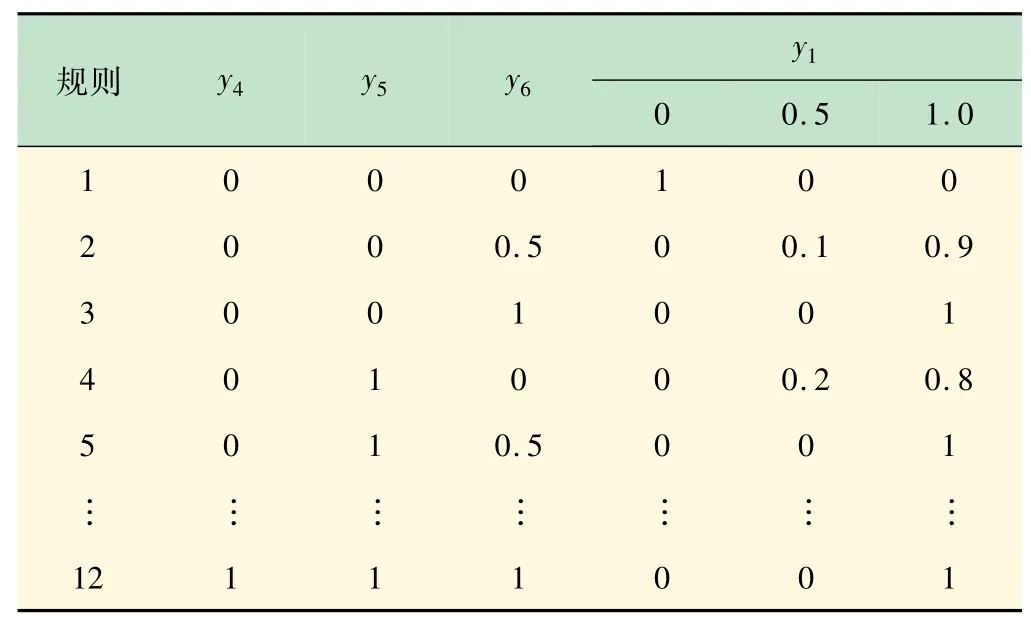
表3 T-S模糊门2

以y11的模糊可能性代替隶属度计算，可得到y3的模糊故障率如下：

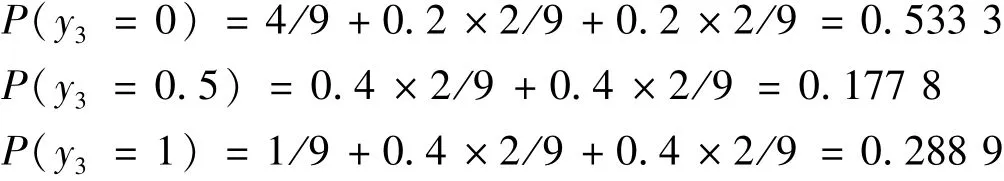
故顶事件故障概率为：

经过分析可知，闸片出现故障时，系统的故障程度与其基本一致。所以可根据部件的故障程度结合T-S模糊故障树得知系统故障可能性。

2.3 基于T-S模糊故障树的制动系统重要度分析

根据式（8）可得x11对T为0.5和1故障状态的TS模糊重要度分别为

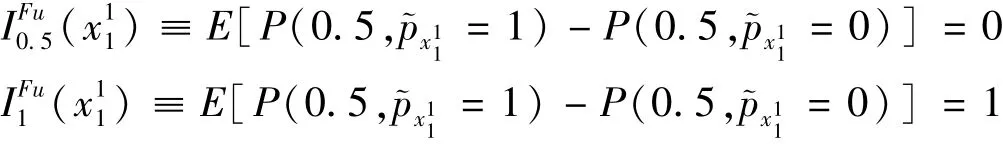
同理得x2～x26的T-S模糊重要度见表7。

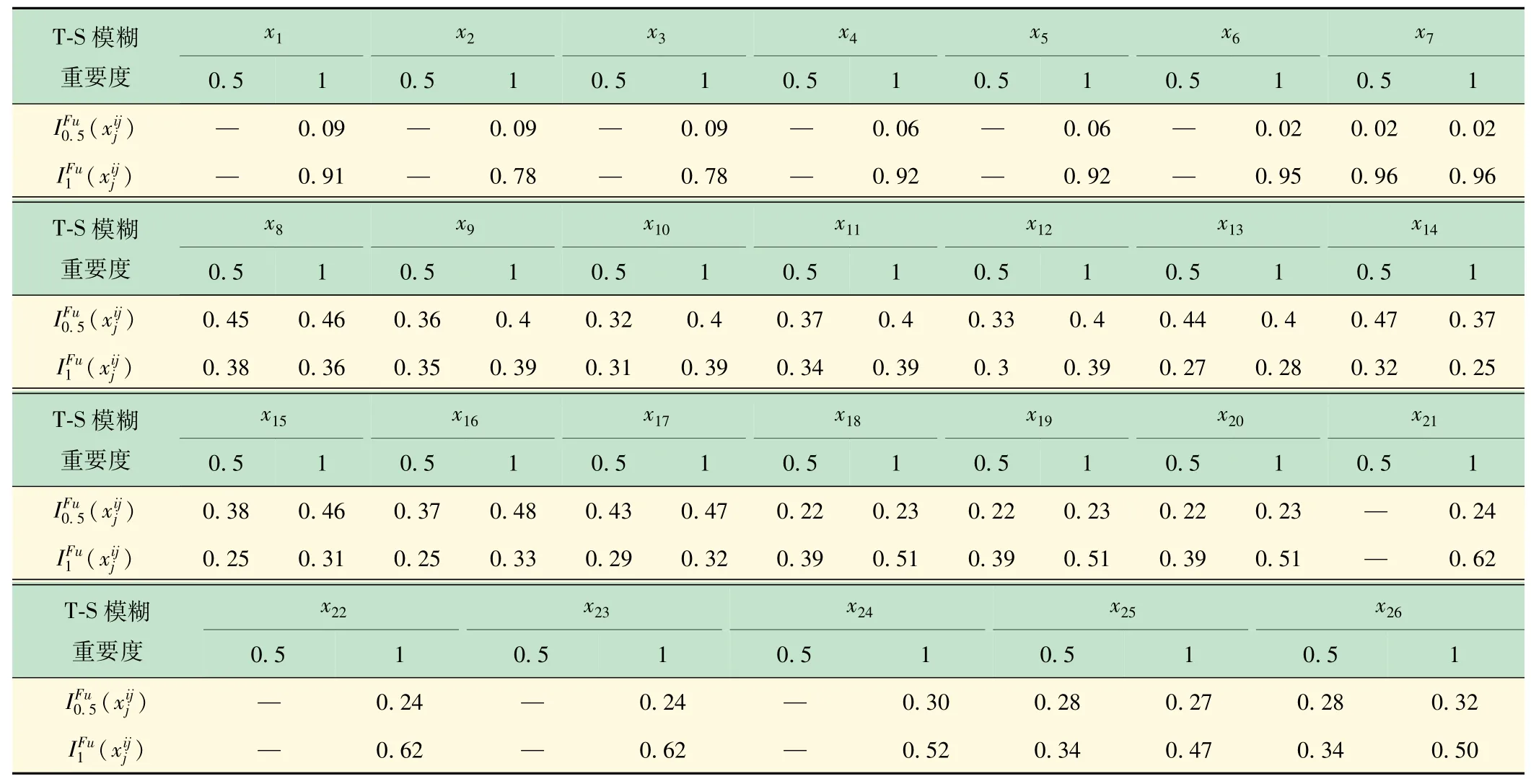
表7 T-S模糊重要度

根据式（9）可得x7对T为0.5和1故障状态的TS概率重要度分别为：

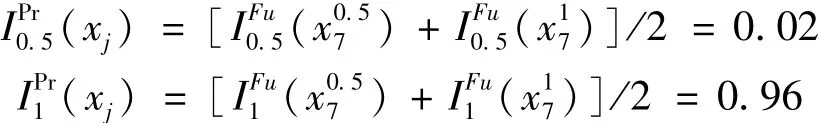
同理得出x1～x26的T-S概率重要度见表8。由表8可知，系统为轻微故障时，重要度大小为x8＞x17＞x16＞x15（x13，x14）＞x11＞x9＞x12＞x10＞x26＞x25＞x18（x19，x20）＞x24＞x21（x22，x23）＞x1（x2，x3）＞x4（x5）＞x7＞x6；当系统为严重故障时，重要度大小为x7＞x6＞x5＞x4＞x1＞x18（x19，x20）＞x26＞x25＞x2＞x3＞x8（x9，x11）＞x10（x12）＞x17（x21，x22，x23）＞x16（x14）＞x15（x13）＞x24。重要度大的部件为系统的薄弱环节，所得结果与实际相符，主要原因是闸片由于过度磨损，常出现缺陷和裂纹，而风管又容易被砂石等击打而导致破裂漏风，空气压缩机经常使用容易出现渗油等现象，因而故障率也较高。

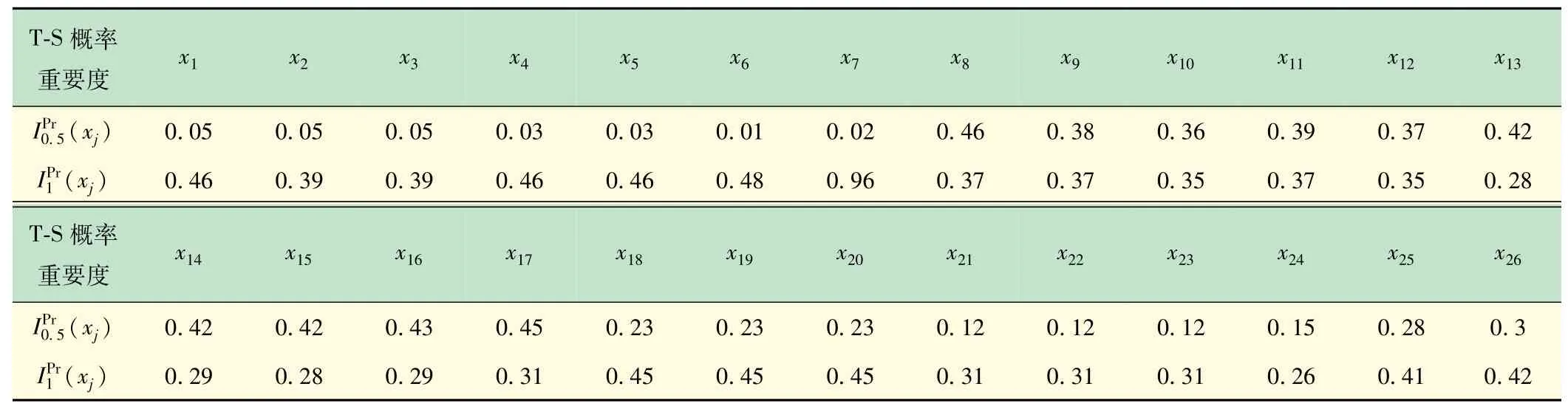
表8 T-S概率重要度

3 结 论

（1）利用T-S模糊故障树对动车组制动系统进行可靠性分析，用T-S模糊门描述事件的逻辑关系，克服了二态失效分析难以找到部件之间紧密联系的局限，综合了所有失效故障状态对系统的影响，所得结果更加符合工程实际且更一般化。

（2）由于T-S模糊故障树逻辑简单紧密，所需数据较少，使故障树建树的难度进一步降低，同时结合基于信心指数修正的专家调查法，得到顶事件的故障率区间和基本事件的模糊重要度，找出了系统的薄弱环节，可为系统检修提供参考。

（3）T-S模糊故障树可在部件失效概率未知的情况下，仅凭借失效部件故障状态计算系统的失效可能性。