基于稀疏贝叶斯学习在未知噪声场的欠定宽带信号DOA估计

郭业才， 田佳佳， 胡国乐

（1.南京信息工程大学电子与信息工程学院，南京210044；2.江苏省大气环境与装备技术协同创新中心，南京210044；3.安徽大学电气工程与自动化学院，合肥230039）

0 引 言

利用传感器阵列估计宽带波达方向（Direction of Arrival，DOA）是一个活跃的研究课题［1］，因为它具有广泛的应用，需要估计所谓的角谱。例如：在雷达、声呐、无线通信和定位等。由于DOA估计准确度是由传感器阵列的自由度（Degree of Freedom，DOF）决定的，均匀间隔阵列需要增加传感器数量才能获得较高的DOF，而提高了制造成本和阵列标定的难度。稀疏阵列，即嵌套阵列和互质阵列［2-3］，可以获得更高的DOF数目，比使用非均匀传感器位置的物理传感器数目解析更多的源。对于稀疏阵列，利用扩展协方差矩阵实现DOF的增加，其虚拟传感器位置由物理传感器之间的连续和非连续滞后差决定。

在稀疏阵列中，互质阵列由于其简单的阵列结构和检测比物理传感器数量更多的信号的能力，引起了人们对DOA估计应用的极大兴趣［4］。利用多个频率来填充缺失的共线阵元，互质阵列可以有效地获得所有提供的DOF，用于高分辨率DOA估计［5］。利用阵列信号模型的稀疏性，稀疏信号表示技术促进了DOA估计的进展［6］。这些基于稀疏信号表示的算法不仅将感兴趣的范围离散为空间角网格，而且假设真实信号DOA必须落在预定义的网格上。然而，在实际情况中，无论网格有多密集，真正的DOA不一定位于准确的采样网格上。这种离网源会导致字典失配问题，不仅违反稀疏性条件，而且会降低性能［7］。Shen等［8］提出了一种基于组稀疏的两步离网源欠定宽带DOA估计方法，该方法比现有的基于组稀疏的同网格搜索方法具有更好的性能。为解决联合稀疏性无法捕获信号真实结构的问题，提出一种稀疏贝叶斯框架内的宽带DOA估计算法，可以更灵活地占用频谱带，并通过在潜在参数空间上施加Dirichlet过程来自动确定潜在的波段占用［9］。

稀疏贝叶斯学习（Sparse Bayesian Learning，SBL）作为一种压缩感知（Compression Sensing，CS）实现，弥补了在联合处理多个频率和多个快照以定位一个或多个源时，多个稀疏解可能对应于一个源的缺点［10-11］。作为一种概率方法，SBL计算稀疏权向量的后验分布，并给出其协方差和平均值［12］。将SBL思想应用于稀疏信号恢复的单测量向量（Single Measurement Vectors，SMV）模型中，通过贝叶斯规则得到后验概率p（x｜y；Θ），Θ为所有超参数［13-14］。超参数是通过在x上进行边缘化，执行证据最大化或ii型最大似然来从数据中估计的［15］。SBL的魅力在于它的全局极小值总是最稀少的一个［16］，而流行的l1-norm优化算法并不是全局收敛［17］。因此，基于SBL的优化算法明显优于传统的l1-norm优化算法。

本文研究了基于互质阵列的SBL算法在未知噪声场中对离网源的欠定宽带DOA估计。互质阵列采用最小稀疏标尺重构空间协方差矩阵，用非均匀采样方法，提倡采集少量样本，避免宽带信号的混叠。将协方差矩阵向量化，利用克罗内克积从互质阵列得到虚拟流形矩阵，利用SBL算法得到宽带信号的DOA估计。在稀疏贝叶斯框架下开发的SBL算法可以近似地解决非凸优化问题，并利用定点更新自动确定稀疏性。基于SBL的宽带DOA估计方案在采集少量样本的情况下，尤其在低信噪比（Signal-to-Noise Ratio，SNR）的情况下，可以提供处理优势。

1 互质阵列的宽带信号模型

一个互质阵列，它包括2个带有N和2M传感器的均匀线性阵列（Uniform Linear Array，ULA），如图1所示。图中，第1、第2个子阵列的元素间距分别为Mλ/2和Nλ/2。λ为信号的中心波长。假设远场K个宽带信源sk（t），k＝1，2，…，K以入射角Θ＝［θ1，θ2，…，θK］射在互质阵列上。在互质阵列的第w个传感器处观察到的信号可以表示为式中：0≤w≤2M＋N－1；sk（t）为第k个信号；nw（t）为未知噪声信号；τw（θk）为第k个入射信号以入射角θk

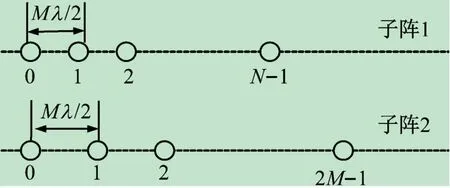
图1 互质阵列模型

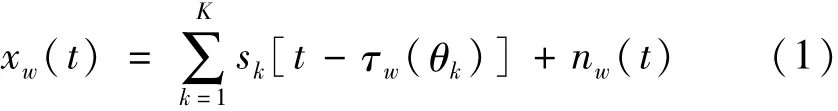
到达互质阵列的第w个传感器的时间延迟。对观察到的传感器信号作L点离散傅立叶变换（Discrete

Fourier Transform，DFT），在频域中，在第w个传感器处接收的数据向量可以表示为

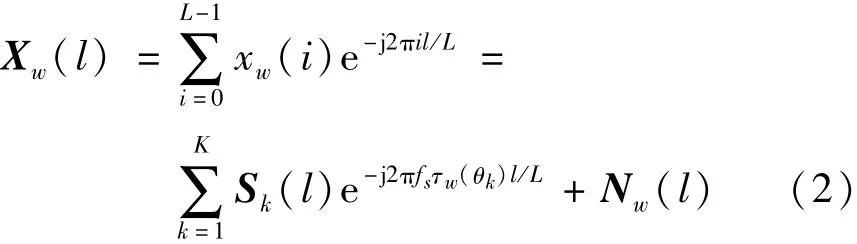
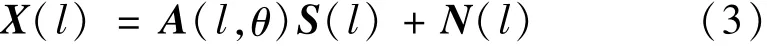
式中：A（l，θ）＝［a（l，θ1），a（l，θ2），…，a（l，θK）］为方向矩阵；a（l，θK）为对应入射角的导向向量。

数据向量的协方差矩阵为

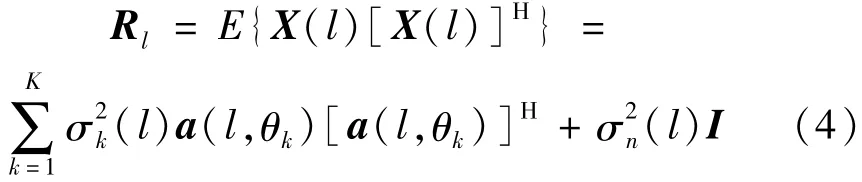
式中：E｛·｝为期望运算符；｛·｝H为厄米转置运算符为第k个信源的方为相应的噪声方差；a（l，θk）为导向向量。在实际情况下，理论协方差矩阵Rl是不可能得到的，可以使用T个可用段（频率快照）估算样本协方差矩阵：

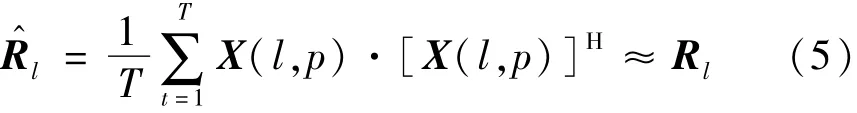
信号协方差矩阵Rl向量化为

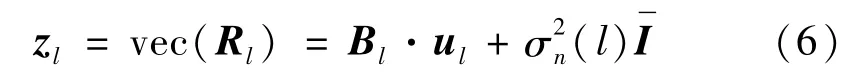
式中：Bl＝［b（l，θ1），b（l，θ2），…，b（l，θK）］为等效导向向量构成的矩阵；b（l，θk）＝a*（l，θk）⊗a（l，θk）为等效导向向量；入射信号方差矩阵和单位矩阵转化后的列向量vec（I）。其中符号‘*’为复共轭；符号‘⊗’为克罗内克积（前一个矩阵中的每一个元素都与后一个矩阵相乘）；vec（·）为将矩阵转化为列向量的操作［18］。

来自矩阵Bl的传感器的位置（被视为较大的虚拟阵列的流形矩阵）在自差分集中

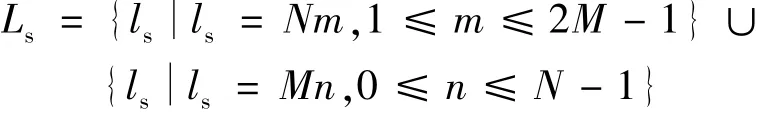
2 带有离网源的稀疏贝叶斯学习

2.1 离网公式

假设存在以lq（q＝1，2，…，Q）为索引的Q≤L个DFT频点。那么对应于Q个频率点的流行矩阵Bl＝［Bl1，Bl2，…，BlQ］。使用固定间隔≤D）的D元素网格θg采样潜在空间域，g为网格，并将网格间隔离散，则式（6）可以写成

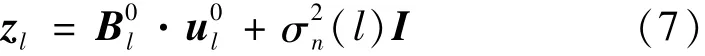
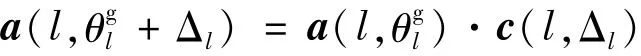
将D个导向向量的集合表示为离网目标下宽带信号的稀疏表示为

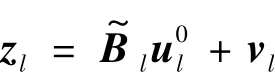
式中，vl为向量，是噪声部分的集合，除第k个条目（对应于nw（t）的第k个元素的方差）外，它由所有零组成。

可见，噪声部分vl可以通过每2个不同的zl之间的计算消除，即式中，m＝1，2，…，h，其中h＝L（L－1）/2。

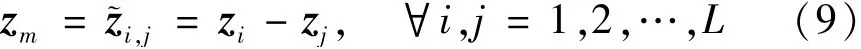
2.2 稀疏贝叶斯学习算法

由于未知噪声通过式（9）得到消除，因此似然概率为

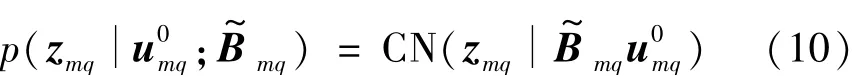
式中：zmq为m点离散傅里叶变换的第q个频点的宽带信号稀疏表示；CN为复高斯分布为m点离散傅里叶变换的第q个频点导向向量的集为m点离散傅里叶变换的第q个频点的方差的稀疏向量。由于为正实数，因此式（10）可以转换为以下实值似然概率为

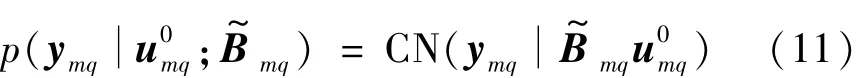
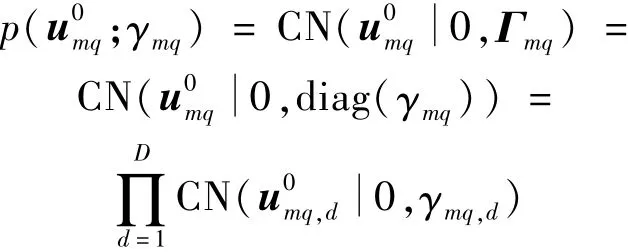
式中：γmq为m点离散傅里叶变换的第q个频点的源方差；Γmq＝diag（γmq，1，γmq，2，…，γmq，D）＝diag（γmq）为在每个范围深度单元θ中以γmq作为源方差的对角协方差；γmq，d为在第d个网格处的源方差。

令Ymq＝｛y1q，y2q，…，yhq｝为T个快拍的集合，而源方差向量的相应集合为使用式（11），多重快照似然概率为

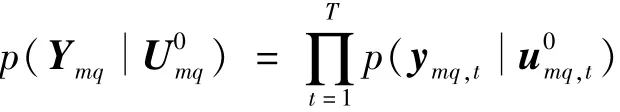
多频似然概率为

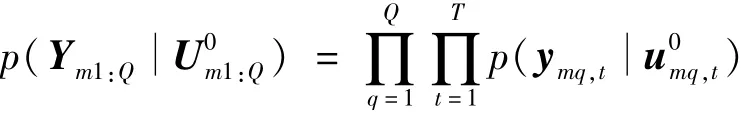
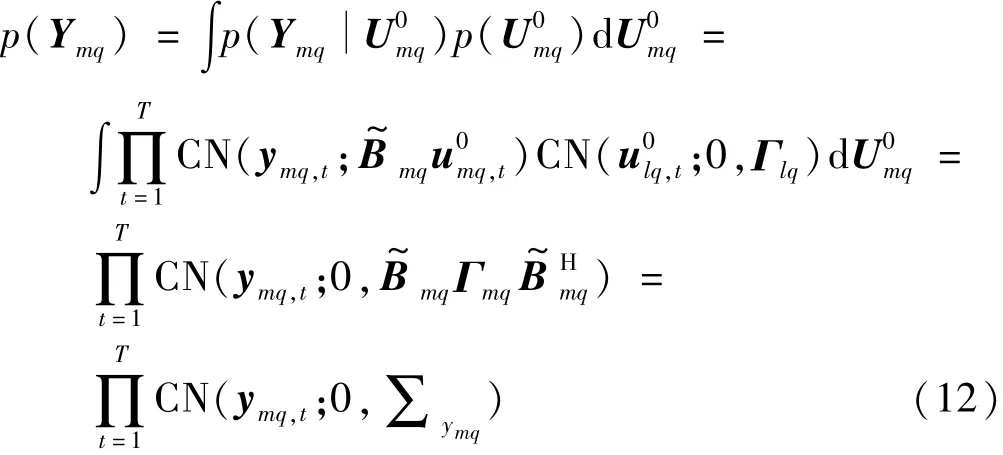
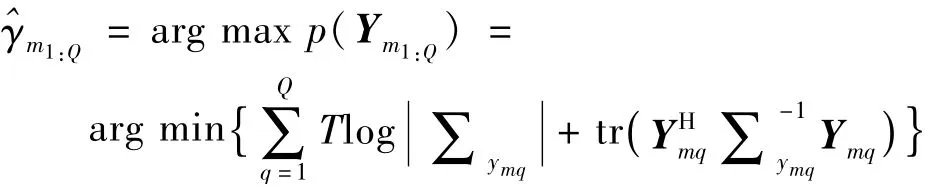
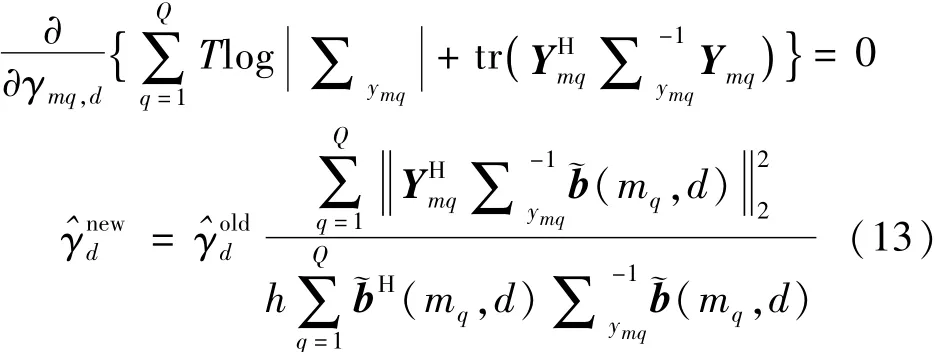
简而言之，SBL算法可以总结如下步骤：

步骤1初始化＝1。

步骤2输入

步骤3通过式（13）更

步骤4如，停止。

步骤5和Nt＝Nt＋1。

步骤6如果Nt＜1 000，返回步骤2；否则停止。

3 仿真结果

在本节中，将通过仿真来说明用于宽带DOA估计的带互质阵列的SBL算法的性能，并将其与其他最新算法进行比较，包括同时正交匹配跟踪最小二乘（Simultaneous Orthogonal Matching Pursuit Least

Squares，SOMP-LS）、同时正交匹配跟踪总最小二乘（Simultaneous Orthogonal Matching Pursuit Total Least Squares，SOMP-TLS）［21］和离网稀疏贝叶斯推理（Offgrid Sparse Bayesian Inference，OGSBI）［22］。在仿真中，信号的分数带宽（即带宽与中心频率的比值）。采样频率是最高频率的3倍。换言之，信号具有从的归一化频率范围，其中归一化频率，其中f是感兴趣的频率。考虑在每个频率点的信号共享相同的分布，即，振幅是瑞利随机变量，并且相位均匀地分布在［－π，π］上。应用L＝128点DFT，感兴趣的频带覆盖Q＝26个频点。假设有一个K＝12信源的示例，它们的离网冲击角均匀地分布在之间。互质阵列由M＝3和N＝4的一对稀疏线性阵列（ULA）组成，一共有9个物理传感器，其位置设置为S＝［0，3，4，6，8，9，12，16，20］λ/2。

比较SBL与SOMP_LS、SOMP_TLS和OGSBI在互质阵列中对欠定宽带DOA估计的检测性能。在整个感兴趣的频带内，信号功率和噪声功率用来计算信噪比SNR。假设K＝12个宽带信源入射到M＝3、N＝4的互质阵列上，快拍数为100，输入信噪比SNR固定为0 dB。如图2所示，SBL与SOMP_LS、SOMP_TLS和OGSBI可以成功的区分出所有的宽带信号（信源数超过物理传感器的数量）。如图2（a）所示，即使SBL在0rad处也存在一个伪峰，而图2（b）、（c）中SOMP_LS和SOMP_TLS没有生成伪峰。如图2（d）所示，OGSBI会生成一些明显的虚假峰。与SBL相比，在某些角度上，SOMP-TLS提供了更接近真实值的DOA估计，而对于其他角度，SBL则提供了更好的准确度。因此，使用SBL和SOMP-TLS算法的估计性能是可比的，并且在其他算法中可提供最佳检测。

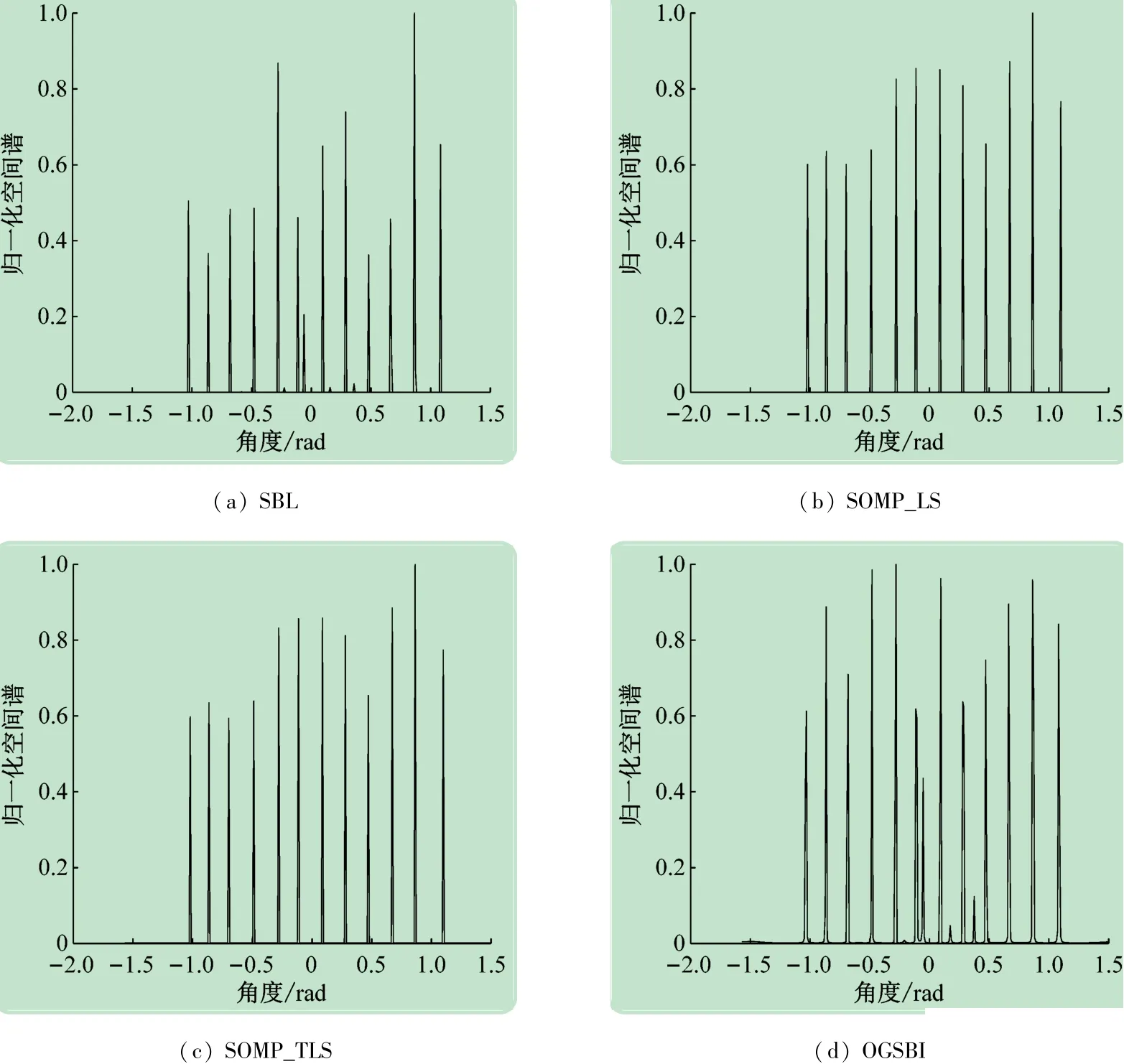
图2 4种算法在快拍数为100，SNR＝0 dB时DOA估计的归一化空间谱

为更加具体地观察出4种算法在互质阵列上对宽带信号的检测性能，表1列出了4种算法的检测结果和待估计DOA。表1表明，SBL算法在绝大多数待估计角度检测中的表现出优于其他3种算法的性能，检测结果的误差均小于其他3种算法。根据均方根误差（Root Mean Square Error，RMSE）将SBL算法与SOMP_LS，SOMP_TLS和OGSBI算法进行比较，以评估算法的估计精度。用RMSE作为DOA性能评估指标，且

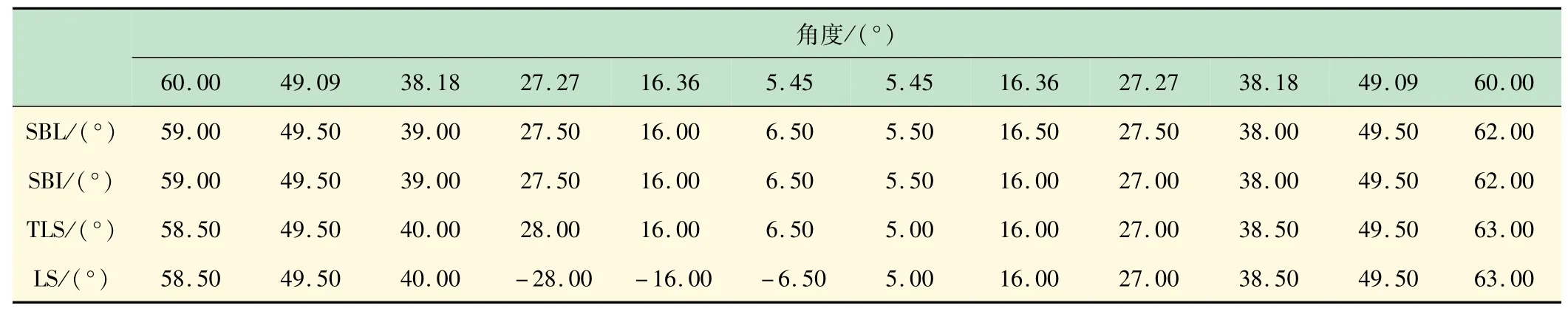
表1 4种算法在SNR＝0 dB，快拍数为100时的角度估计

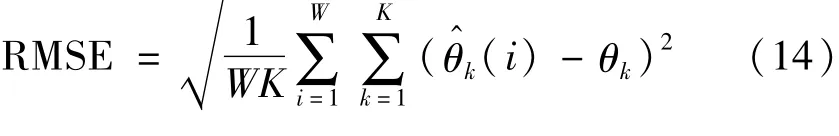
式中：W为独立的蒙特卡洛试验的数为第i个蒙特卡洛试验的θk的估计值。这里，每个测试点均采用200次蒙特卡洛模拟迭代的平均结果。Crame-Rao下界（CRLB）［23-24］（它提供了估计准确性方差的下界）也用于表示理想估计。

如图3所示，在快拍数为200时，4种算法随信噪比的变化，SBL算法的仿真结果表现出比其他3种算法更好的估计性能，尤其是在低信噪比时，SBL算法的RMSE明显小于其他3种算法，在宽带信号的DOA估计上表现出更好的性能。

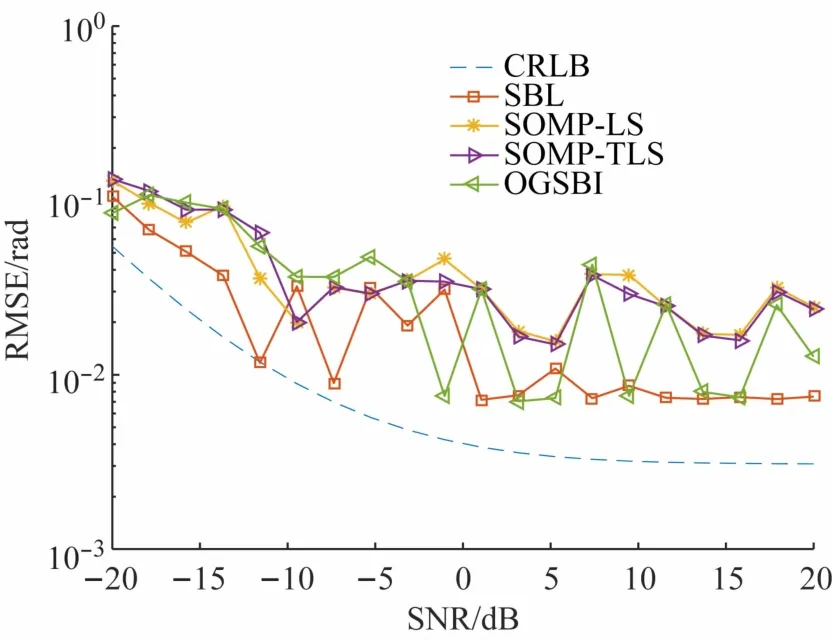
图3 快拍数为200时，4种算法的RMSE随SNR的变化

如图4所示，在信噪比为0dB时，SBL算法的性能明显优于其他3种算法，在相同条件下，SBL算法的均方根误差最小，准确率更高。

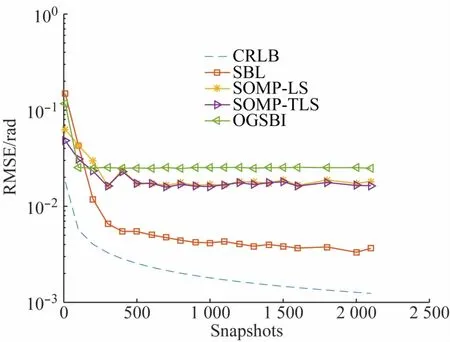
图4 SNR＝0 dB时，4种算法的RMSE随快拍数的变化

4 结 语

通过使用SBL算法进行基于互质阵列的欠定宽带在未知噪声场中的DOA估计，与SOMP_LS，SOMP_TLS和OGSBI算法相比，SBL表现出出色的检测性能和估计准确度。SBL可以容纳由互质阵列提供增加的DOF，对欠定宽带进行有效的DOA估计，通过互质阵列提供的虚拟阵元接收更多的宽带信号并且通过每2个向量化函数之间的运算消除未知噪声。本文采用了定点更新为宽带DOA估计提供全局收敛性。仿真和实验结果表明，本文算法有着更好的抗噪能力。