环锭纺钢丝圈空间运动理论模型的优化

刘汉邦，李新荣，冯文倩，吴柳波

(a.天津工业大学 机械工程学院；b.天津市现代机电装备技术重点实验室：天津 300387)

1 概述

未来很长一段时间内，占据我国纺纱行业主导地位的仍将是环锭纺纱。随着高速纺纱锭子技术的逐渐发展并趋于成熟，环锭纺纱朝着高速化、大卷装和高产能方向发展，而限制环锭纺高速发展的因素主要为钢领、钢丝圈系统。钢丝圈的空间运动状态对环锭纺细纱机的成纱质量、纺纱断头率及钢丝圈的设计使用等均有重要影响，因此，针对钢丝圈在纺纱过程中运动状态的研究具有重要意义。在纺纱过程中，要研究分析钢丝圈的空间运动状态，就需要对钢丝圈进行受力分析，建立钢丝圈受力动平衡方程，而气圈段纱线张力[1]会随其形态产生变化，直接对钢丝圈受力情况造成影响。因此，在研究钢丝圈空间运动状态的过程中，必须与气圈理论相结合[2]，两者相辅相成，不可分割。

我国研究机构一般在不计空气阻力和科里奥利力[3-5]对纱线影响的情况下，建立气圈段纱线曲线形态方程，并给出其近似解。一些欧美学者考虑空气阻力对环锭纺纱中气圈的影响，研究关于气圈段纱线的张力，但是分析中却指出气圈高度和锭子转速对气圈影响较小。Batra等[6-7]将建模分析法运用到纺纱研究过程，由于气圈形态的复杂性，只能得到数值解。Fraser等[8-9]分析纱线本身的不均匀性、气圈控制环等条件对环锭纺纱线气圈形态和稳定性的影响。Tran等[10-11]采用了神经网络算法对忽略空气阻力影响下的纺纱气圈数学方程模型进行数值模拟。环锭纺纱过程中纱线张力分布和气圈形状随纺纱速度变化的数学模型,由德国德累斯顿理工大学的Mahmud Hossain等[12-13]提出，该数学模型的计算结果较为准确，但模型中方程的求解对初始值的依赖性很强。

鉴于先前研究中存在的不足，笔者提出了一种灵敏度分析的算法来预测初值的正确选择，从而找到一个稳定的解。与传统模型相比，笔者考虑了空气阻力及科氏惯性力对气圈的影响，并对钢丝圈进行受力分解，将各力分解到3个空间坐标平面上[14-16]，分别建立3个平面上的力矩平衡方程。然后将得到的力和力矩代入力矩平衡公式，即可得到钢丝圈空间倾角变化规律。基于图像处理技术，对高速相机拍摄到的图片进行特征提取，然后对钢丝圈实际倾角变化与理论模型得到的结果进行对比验证，分析造成误差的原因，在此基础上进一步优化钢丝圈空间运动模型。

2 环锭纺钢丝圈运动分析

2.1 钢丝圈空间倾角分析

为研究钢丝圈空间倾角变化规律，将它某一时刻的空间倾斜状态分别向3个空间坐标平面内投影。钢丝圈在3个坐标平面上的倾斜分别称为外脚下沉(见图1)、外脚超前(见图2)和整体前倾(见图3)，而其倾角分别称为外倾角τ、超前角γ和前倾角λ。在回转的过程中，将钢丝圈的倾斜运动分解为这3种运动，为方便计算，假设3种运动独立发生。

图1 钢丝圈外脚下沉

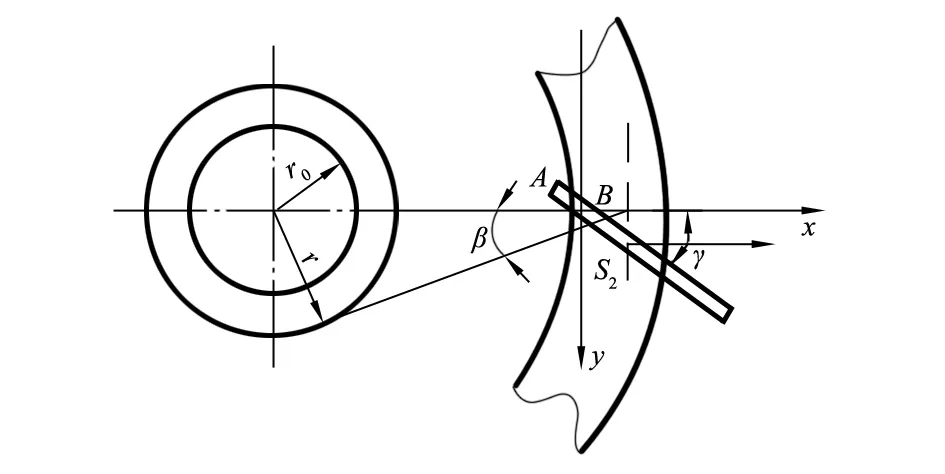
图2 钢丝圈外脚超前

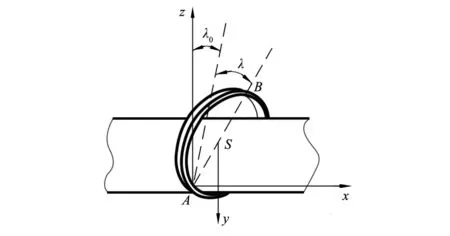
图3 钢丝圈整体前倾

钢丝圈从初始状态只绕y轴偏转角度τ，即只发生外脚下沉而不发生外脚超前和整体前倾，如图1所示，此时钢丝圈的质心位置是S1(x1，0，z1) ：

x1=a0sin(τ0+τ)

y1=0

(1)

z1=a0cos(τ0+τ)

式中：

a0——质心S0到接触点A的距离/mm；

τ0——AS0与z轴夹角。

此时纱线与钢丝圈接触点B的坐标为B1(xb1，0，zb1)，l为A，B两点间的距离：

xb1=lsinτ

yb1=0

(2)

zb1=lcosτ

在外脚下沉的同时，钢丝圈发生外脚超前，其绕z轴偏转角度γ，如图2所示，此时钢丝圈的质心位置是S2(x2，y2，z2)：

x2=x1cosγ=a0sin(τ0+τ)cosγ

y2=x1sinγ=a0sin(τ0+τ)sinγ

(3)

z2=z1=a0cos(τ0+τ)

此时纱线与钢丝圈接触点B的坐标为B2(xb2，yb2，zb2)：

xb2=xb1cosγ=lsinτcosγ

yb2=xb1sinγ=lsinτsinγ

(4)

zb2=zb1=lcosτ

发生外脚下沉和外脚超前的同时，钢丝圈还发生整体前倾，其再绕x轴旋转角度λ，如图3所示，此时钢丝圈的质心位置就是实际位置S(x，y，z)：

x=a0sin(τ0+τ)cosγ

(5)

同理，此时纱线与钢丝圈接触点B的实际空间坐标为B(xb，yb，zb)：

xb=lsinτcosγ

(6)

而角度λ0通过计算可求得：

(7)

通过以上分析可知，质心位置S和纱线与钢丝圈接触点B都是关于τ，γ，λ变化的量。但对于钢丝圈3个空间倾角的计算，还需要通过对钢丝圈进行受力分析才能得出。

2.2 钢丝圈受力分析

2.2.1 钢丝圈离心力

以钢领板的每一次短动程起始点为坐标原点，建立直角坐标系，如图4所示，为钢丝圈回转和钢领升降示意。钢丝圈骑跨在钢领上，随钢领板做升降运动，同时高速回转，所以为了保持纱线在纱管上圆锥形卷绕且圆锥面各处卷绕密度相同，钢丝圈随钢领升降的速度应满足式(8)所示要求。

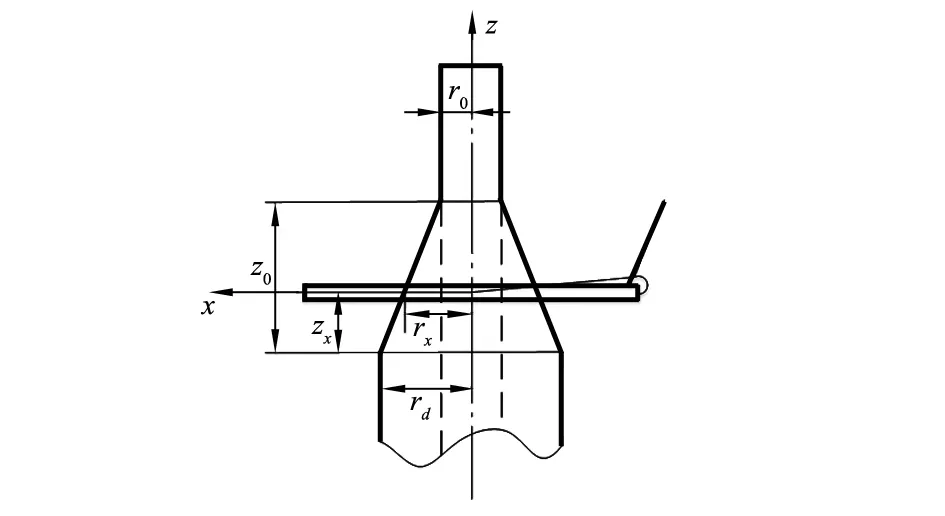
图4 钢丝圈回转和钢领升降

(8)

式中：

vz——钢领板升降速度/(m·min-1)；

q——细纱卷绕圈距/mm；

vs——输出纱线速度/(m·min-1)；

rx——卷绕半径/mm。

从图4中可知：

(9)

式中：

zx——钢领板在t时的高度/mm，钢领板运动方向沿着坐标轴z轴。

为了将圆锥形状保持不变，在纺纱过程中，钢领板升降速度vz和卷绕半径rx应满足相应的规律关系。由此可得rx计算公式：

(10)

式中：

rd——管纱最大半径/mm；

r0——空纱管半径/mm。

正常卷绕时，细纱的卷绕速度nw等于锭子速度ns与钢丝圈速度n之差，因此，钢丝圈的离心力C为：

(11)

式中：

m——钢丝圈质量/mg；

L——钢丝圈回转半径/mm，L=rr+lsin(τ0+τ)；

rr——钢领半径/mm。

2.2.2 气圈底端张力

如图5所示，建立一个静坐标系Φ(r，ζ，z)，坐标原点为导纱钩的中心点，z轴的正方向为竖直向下，且与纱线筒管的中心线重合。在静坐标系坐标原点处，新定义一个动坐标系R(r，θ，z)， 并以角速度ω绕z轴旋转。文中关于纱线微元的分析都是在动坐标系R(r，θ，z)下完成的。由此可以得到两个坐标系之间的相对位置关系表达式：

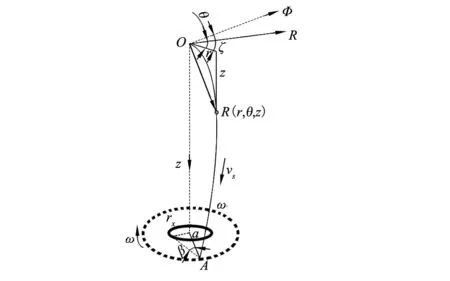
图5 气圈坐标系

ζ=θ+ωt

(12)

式中，t表时间。

在该动坐标系中分析时，卷绕段的纱线被看做是一条静止的空间曲线。取er，eθ，ez分表代表单位径向量，单位角向量，z轴单位向量。在纱线气圈上任取一点R，且到坐标原点的纱线长度为s，位置矢量R表示如下：

R=rer+zez

(13)

气圈上纱线的单位切向量τ表示为：

(14)

由于底端张力与输出纱线的速度vs有关，故根据图5分析可得：

(15)

如图6所示，在纱线气圈上取微元段ds进行分析，它的力平衡方程为：

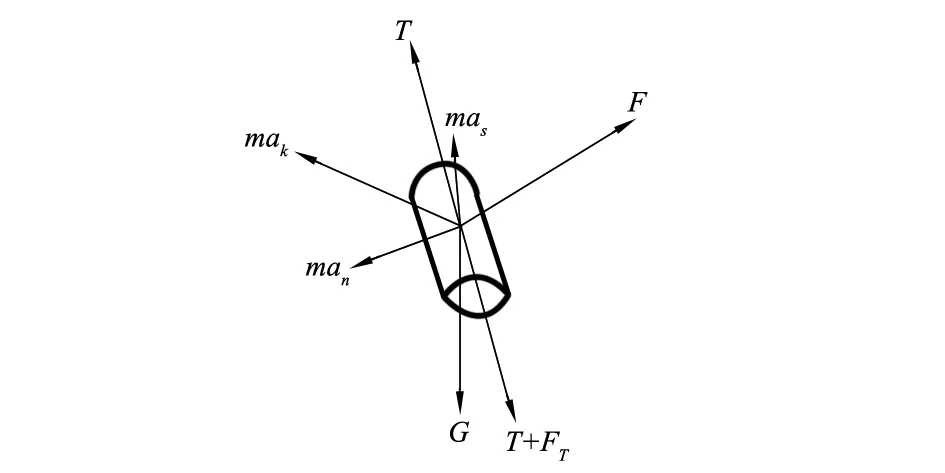
图6 纱线微元受力示意

m0(an+ak+as)ds=(FT+F)ds

(16)

式中：

m0——纱线线密度/(g·cm-1)；

an——纱线向心加速度/(m·s-2)；

ak——纱线科氏加速度/(m·s-2)；

as——纱线相对加速度/(m·s-2)；

FT——单位长度上纱线张力增量；

F——纱线微元的外力/N。

其中：

an=-ω2rer

(17)

(18)

(19)

纱线张力和张力增量的表达式为：

T=Tτ

(20)

[T(2r′θ′+rθ″)+T′rθ′]eθ+[Tz″+T′z′]ez

(21)

作用在纱线微元段上的力还有空气阻力：在切向上的粘滞力Fτ和在垂直方向上的正压力Fn。法向空气阻力系数是切向的20倍，因此，我们只考虑前者对纱线微元的影响。

Fn=-pn|vn|vn=pnr2ω2(r′2+z′2)×

(22)

式中：

pn——法向空气阻力系数。

根据纱线微元受力及加速度公式，方程(16)在坐标轴下的分量方程为：

(23)

由于纱线是柔性无伸长的，因此可得：

(24)

法向空气阻力方向垂直于纱线，因此：

(25)

对纱线微元的力平衡方程(16)点乘dR/ds，因此：

T′=-m0ω2rr′-m0gz′

(26)

忽略纱线重力，由边界条件，在导纱钩处r=0，此时T=T0。对上式积分可得：

(27)

式中：

T0——导纱钩处的纱线张力/N。

钢丝圈处纱线微元的卷绕半径为L，纱线微元回转角速度即为钢丝圈的回转角速度，由此可得气圈底端张力：

(28)

2.2.3 气圈卷绕张力

纱条的卷绕张力Tw可近似看成作用在钢丝圈的回转平面上，由此，可分解为径向分力和切向分力，即：

(29)

式中：

β——卷绕张力Tw与x轴夹角，即卷绕角。

钢丝圈受力分析见图7。

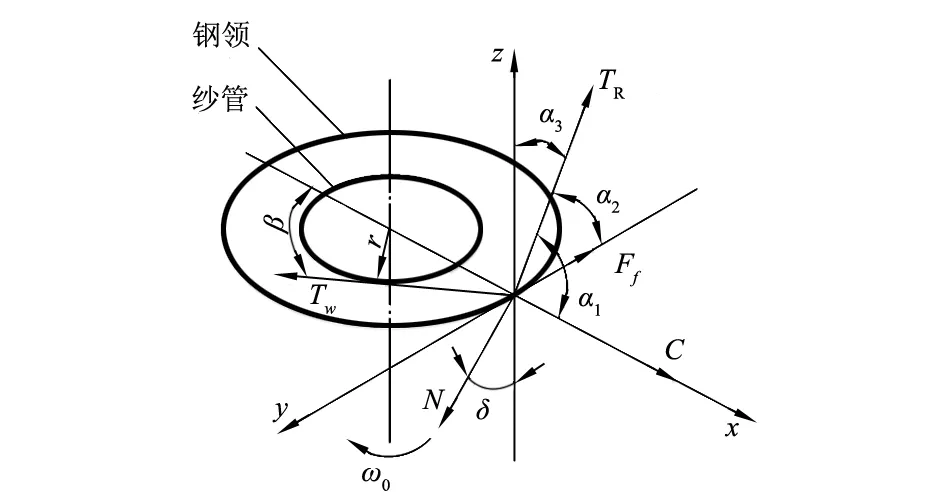
图7 钢丝圈受力分析

由图7可知，气圈底端张力TR与x，y，z轴的夹角分别为α1，α2，α3。且有：

cos2α1+cos2α2+cos2α3=1

(30)

纱穿过钢丝圈内通道时因受到钢丝圈接触面上的摩擦形成松紧边，可得到卷绕张力[17]：

Tw=TReμ1φ=KTR

(31)

cosφ=cosα1cosβ+cosα2sinβ

(32)

式中：

μ1——纱与钢丝圈表面的摩擦因数；

φ——纱在钢丝圈截面上的包围角；

β——卷绕张力Tw与x轴的夹角，即卷绕角。

2.2.4 各力与坐标轴间的夹角

将各力分解在空间坐标轴进行研究，如图7所示。钢丝圈离心力C沿着回转半径方向向外，与x轴重合，方向与x轴正方向一致。摩擦力Ff与运动方向相反，与y轴重合，方向与y轴正方向相反。TR，Tw，N与空间坐标轴间夹角如图7所示。

根据力学平衡原理，可以得到如下关系：

Twcosβ+Nsinδ-C-TRcosα1=0

TRcosα2+Ff-Twsinβ=0

(33)

TRcosα3-Ncosδ=0

根据钢丝圈受力平衡方程，可得钢丝圈支撑力N和z轴的夹角δ为：

(34)

将公式(23)整理可得：

(35)

为使气圈数学模型有解，须确定其边界条件。

a) 在导纱钩处满足初值条件：

r(0)=0;θ(0)=0;z(0)=0

(36)

b) 在钢丝圈处满足边值条件：

r(sl)=L;z(sl)=H-Hx

(37)

式中：

H——t=0时刻气圈高度/mm;

sl——使数学模型有解的一个数值。

c) 在对纱线气圈进行分析时，假设纱线是均匀的柔性体，并且纱线无伸长。由此可得TR与空间3个坐标轴之间夹角的计算公式：

(38)

根据纱线微元分析，由纱线切向量公式(14)和坐标转换原理可知，在钢丝圈处有：

cosα1=r(s1)′

cosα2=Lθ(s1)′

(39)

cosα3=z(s1)′

由钢丝圈受力，以及钢丝圈倾角分析，得出钢丝圈的力矩平衡方程：

CZ+TRcosα1Zb-TRcosα3Xb-TwcosβZb=0

TwcosβYb+TwsinβXb-TRcosα2Xb-TRcosα1Yb-CY=0

TRcosα2Zb+TRcosα3Yb-TwsinβZb=0

(40)

将钢丝圈受到的各力、钢丝圈质心、钢丝圈与纱线接触点坐标，以及各力与坐标轴的夹角代入钢丝圈力矩平衡公式，即可得出钢丝圈空间倾角τ，γ，λ的数值大小及其随时间的变化。

3 仿真及参数分析

3.1 参数设定

在对钢丝圈空间运动模型进行参数分析时，相关参数的选取必须满足一定的实际条件：选取的参数理应是空间运动模型数值求解中必需的常量值，这些参数对纺纱过程影响较大。求解分析过程中设置的参数如表1所示。

表1 参数及参数值的设定

3.2 各参数对空间倾角的影响

3.2.1 锭子转速的影响

通过6组锭速值分析锭子转速对钢丝圈空间倾斜角度的影响，每组锭子转速(kr/min)取值分别为16，17，18，19，20，21，其他参数值见表1。在MATLAB分别绘制外倾角、超前角和前倾角随时间运动的变化规律，见图8。

由图8a)可知，锭子转速越高，钢丝圈的空间外倾角越大，但是外倾角变化范围越小。由图8b)可知，当转速达到18 kr/min以上时，超前角γ在0°左右波动，说明钢丝圈高频振动，其运动不稳，有可能导致钢丝圈飞圈，这个结果也与实际纺纱问题相符。 由图8c)可知，当转速为20 kr/min时前倾角λ在0°附近，超过这个转速，钢丝圈前倾角变为负值，即钢丝圈发生后倾。

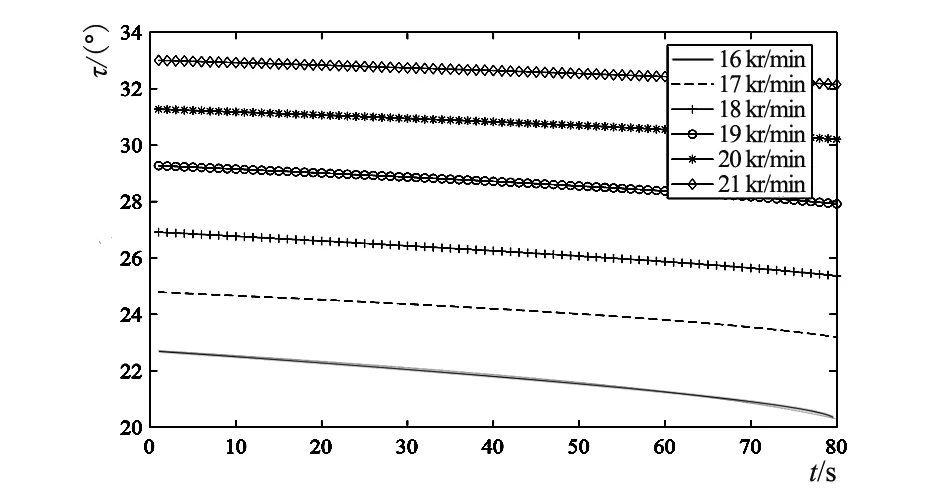
a) 不同锭子转速外倾角变化示意

3.2.2 钢丝圈质量的影响

通过6组钢丝圈质量值分析钢丝圈质量对钢丝圈空间倾斜角度的影响，每组钢丝圈的质量(mg)分别为20，50，80，140，180，250，其他参数值见表1。在MATLAB分别绘制外倾角、超前角和前倾角随时间的运动变化规律，见图9。

由图9可知，当钢丝圈质量超过一定值的时候，增加其质量，使外倾角、超前角、前倾角趋于稳定。3.2.3 钢领半径的影响

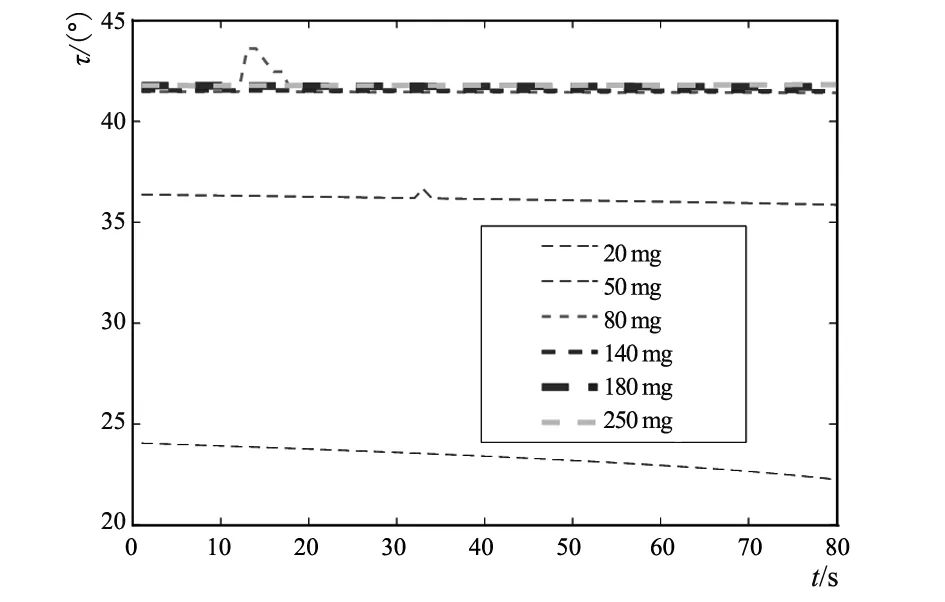
a) 不同钢丝圈质量外倾角变化示意

钢领直径一般在36 mm～57 mm，取6组钢领内径值分析钢领半径对钢丝圈空间倾角的影响，每组钢领半径(mm)分别为18，20，22，24，26，28，其他参数值见表1。在MATLAB分别绘制外倾角、超前角和前倾角随时间的运动变化规律，见图10。

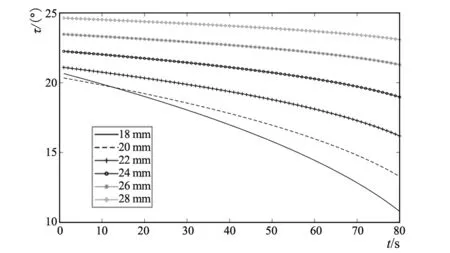
a) 不同钢领半径外倾角变化示意

由图10a)可知，在1个短动程时间段内，外倾角随时间减小，随钢领半径增加而增加。但当钢领半径增加时，外倾角在1个短动程时间内的变化幅度减小。由图10b)和图10c)可知，超前角和前倾角随着钢领半径的增加而减小。

3.2.4 钢丝圈a0尺寸的影响

取6组值分析尺寸a0对钢丝圈空间倾角的影响，每组a0值(mm)分别为1.5，1.6，1.7，1.8，1.9，2.0，其他参数值如表1所示。在MATLAB分别绘制外倾角、超前角和前倾角随时间的运动变化规律，见图11。

由图11a)可知，随a0尺寸增加，同样参数条件下的外倾角数值增大。由图11b)可知，随着a0尺寸的增大，超前角减小，但是超前角降低值较小。由图11c)可知，在1个短动程时间段内，前倾角λ的数值随时间增加，且其随a0尺寸增大而降低，降低幅值相对超前角来说要大一些。

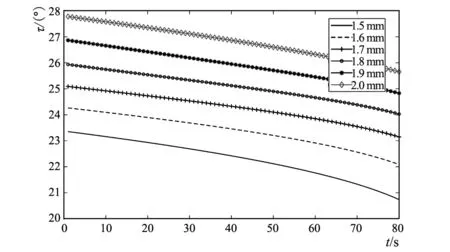
a) 不同a0外倾角变化示意

4 实验及结果分析

4.1 实验过程

环锭纺细纱机进行纺纱，用高速相机拍摄钢丝圈运转过程的照片，基于图像处理技术，对高速相机拍摄到的图片进行特征提取，研究钢丝圈运转过程中的实际倾斜角度。实验设备主要有两部分：实验硬件、图像分析软件。根据本实验过程方案的要求，选择了Vision Research公司的V411系列高速相机，拍摄分辨率及帧率可根据需要调整。实验过程中，调节分辨率为1024×1024，帧率为6400 FPS，并安装配套镜头以及公司专门的PCC控制软件。纺纱实验中的主要参数同表1。

在图像处理过程中，我们主要对钢丝圈的外倾角及其前倾角进行拍摄运动图像，通过这两个角度的图像处理分析结果来验证理论模型。图12为钢丝圈外脚下沉和整体前倾运动图像。

图12 钢丝圈外脚下沉和整体前倾运动图像

4.2 结果分析

现在已经得到1个短动程时间段内的钢丝圈外倾角及其前倾角的数据，为了更直观的观察两个角度随时间的变化，以及为了与两者理论的变化曲线进行对比，将数据输入MATLAB，进行数据点折线连接，见图13、图14。

图13 外倾角的实验值与理论值对比

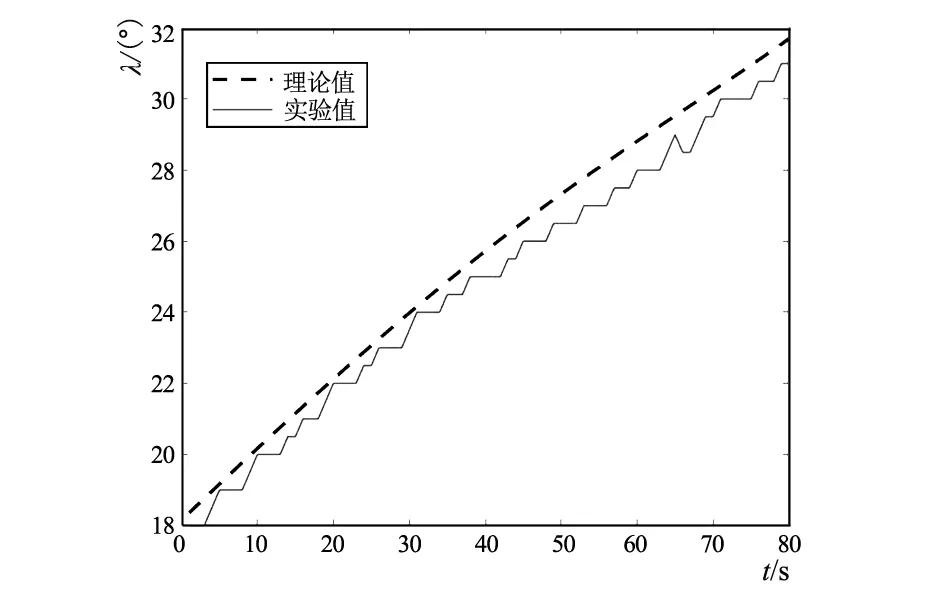
图14 前倾角的实验值与理论值对比

由图13、图14可看出，实验值与理论值相近，两者随时间变化的趋势走向相同，两者之间的差值在可接受的范围内。

5 结论

5.1针对环锭纺的加捻卷绕工艺过程进行分析，得出钢领板升降规律，及钢丝圈随钢领板上升时的转速变化过程。分析纱线在管纱上的卷绕成形过程，得出纺纱级升和纱线卷绕半径之间的规律，对气圈段纱线微元分析和钢丝圈受力分析具有重要作用。

5.2对钢丝圈进行受力分析，确定钢丝圈受到离心力、底端张力和卷绕张力。在考虑到空气阻力及科氏惯性力对气圈影响的情况下，对纱线气圈微元段进行分析，建立气圈段数学模型，该模型符合高速纺纱时气圈的实际受力情况；在工艺基础上，进一步确定了离心力和气圈卷绕张力的大小。

5.3将运动学和动力学理论运用到研究中，把钢丝圈的运动过程分解为牵连运动和相对运动，得出钢丝圈高速回转过程中，钢丝圈质心和纱线与钢丝圈接触点的空间坐标随空间倾角的变化过程。

5.4在各力的数值确定之后，研究各力与空间直角坐标系的夹角，建立钢丝圈力矩平衡方程，依次代入各项分析数据，最终得到钢丝圈在回转过程中投影到3个平面上的倾角τ，γ，λ的理论模型。