可靠度分析中拉丁超立方和传统舍选抽样法对比研究
鲍俊文,胡欣宇,邢明源,赵少飞
(华北科技学院 建筑工程学院,北京 东燕郊 065201)
0 引言
自20世纪中期岩土工程领域开展可靠度研究以来,岩土工程可靠度研究成果在工程实践中产生了重大影响。目前,蒙特卡罗(Monte Carlo)方法是可靠度分析中的主要手段之一,还是检验其它可靠度计算方法精度的唯一途径。由于岩土工程存在很多不确定性因素,该方法也大量应用到岩土工程可靠度分析。文献[1]中详细的介绍了该方法的原理。杨明等[2]应用蒙特卡罗法,分析了均质土坡的稳定可靠度。吴振君等[3]应用该方法对边坡工程将进行了可靠度分析,讨论了拉丁超立方抽样(LHS)方法和蒙特卡罗传统抽样计算可靠度指标的各种方法,得到LHS法较传统抽样方法效率上有很大改善。针对蒙特卡罗传统抽样方法计算量大的问题,伍国军等[4]基于拉丁超立方抽样方法编制了有限元可靠度程序。由于蒙特卡罗方法的结果精度主要取决于抽出样本的质量,符蓉[5]对比了拉丁超立方抽样方法与传统抽样方法,得出拉丁超立方抽样方法计算效率明显优于传统抽样方法。曹伟等[6]应用LHS方法进行了边坡可靠度的有限元分析,认为LHS方法相较于传统抽样方法更加高效,且计算结果较为精确。Nguyen和Chowdhury[8]提出一种应用于岩土工程的风险分析方法,得到了良好的结果。
为了对比蒙特卡罗方法中传统抽样方法和拉丁超立方抽样结果的差别,采用Matlab软件进行抽样编程,分析了抽样方法对条形基础极限承载力可靠度结果的影响。
1 蒙特卡罗方法的原理
蒙特卡罗方法需要首先产生随机变量样本,然后计算得到函数的样本,进而统计失效区域的样本数来估计失效概率,该方法的优点是概念清晰,易于使用。这种方法的主要缺点是用于准确估计失效概率的样本数应足够大。这必然导致过大的计算量[1]。

可以写成
(1)
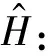
(2)
其中,xi是sx(x)的一个样本,N为样本总数。
蒙特卡罗法实施即为上述计算积分过程。对于工程失效概率Pf
(3)


(4)
因为I(x)服从二项分布且参数为Pf,其方差为NPf(1-Pf)。Pf是I(x)的均值,Pf的方差可以估计为
(5)
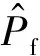
(6)
2 传统舍选法和拉丁超立方法原理
蒙特卡罗传统抽样方法有逆变换法和舍选法,由于逆变换法有一定的条件限制,适用于随机变量X具有累积分布函数表达式情况。而舍选法仅需要随机变量的概率密度函数表达式,本文选用舍选法与拉丁超立方抽样方法进行对比。
2.1 舍选法
假如hX(x)和sY(y)为两个概率密度函数。先从sY(y)抽取样本,然后按下面步骤对生成的样本进行选择,使得选出的样本分从hX(x)的分布。具体抽样步骤如下:
10.秋季仔猪容易发生猪瘟、霉菌中毒、圆环病毒病、副伤寒、猪流感、喘气病、蓝耳病及球虫病,故建议在此期间针对性的不间断投服“金泰妙(45%泰妙菌素可溶性粉)”、 “金奇氟(20%替米考星)”、伊爱尔(0.6%伊维菌素预混剂)、“氟力佳(20%氟苯尼考可溶性粉)”,连用5~7 d。
(1) 在sY(y)中抽取一个样本为y*。
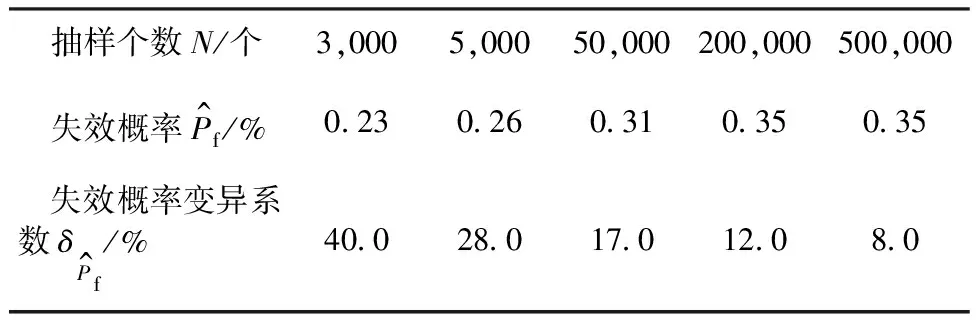
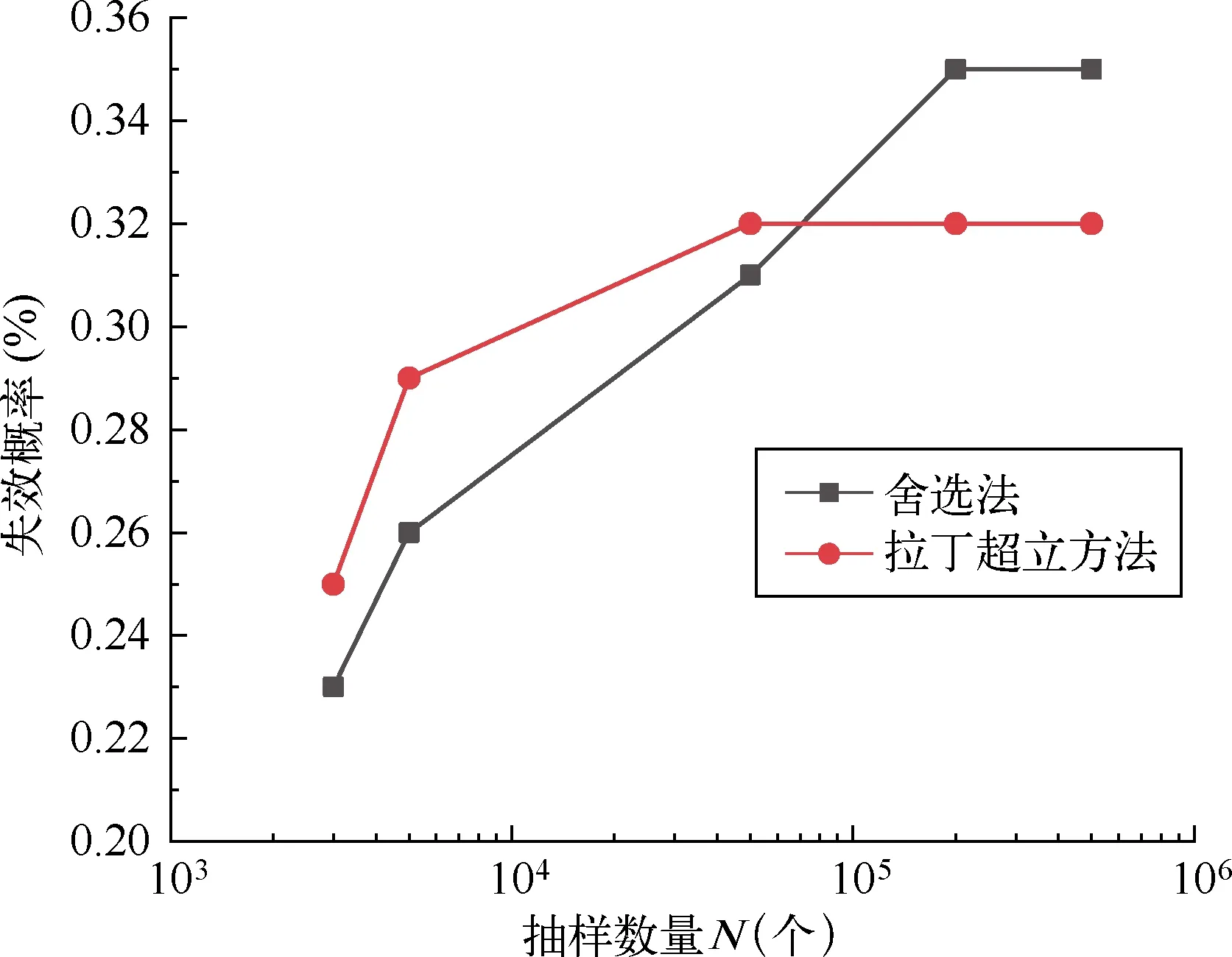
(2) 在均匀分布[0, 1]区间随机抽一个样本u,若u (3) 再重复(1)步骤就可以得到需要的样本数量。 在给定抽样函数情况下, 拉丁超立方抽样方法更能代表抽样函数。对于n个相互独立的随机变量X1,X,…,Xn,抽样的具体实施步骤如下: (1) 每一个随机变量Xk被分成M个区域,使得xk1 (2) 假定U是服从[0,1]区间上的均匀分布,从中抽取一个样本u,在每个区域中抽取Xk在第m个区间段抽取的样本为 (7) 在整个区间,共抽取随机变量Xk的M个随机变量。 岩土工程中,条形基础的极限承载力常用Hansen公式计算,极限承载力qu为 qu=0.5γBNγ+cNc+γmdNq (8) 图1 承受均布荷载的浅基础 以某一条形基础为例[1],基础宽度为2m,埋深为0.5m,土的重度均取20kN/m3,黏聚力和内摩擦角为随机变量,服从正态二元分布,黏聚力的均值和标准差分别为20kPa和5kPa,内摩擦角的均值和标准差分别为30°和6°,两者的相关系数为-0.5。根据Hansen公式计算的极限承载力qu的均值为1148.5kPa,基础承受的荷载q为1000kN/m。 用传统舍选法,随机抽样数量分别为3,000、5,000、50,000、200,000和500,000,计算该浅基础相应的失效概率和变异系数,结果如表1所示。 表1 传统舍选法结果 对于上述算例,假设粘聚力和内摩擦角相互独立,在拉丁超立方抽样中M取5,为了对比两种抽样方法,抽样数量一样,分别为3,000、5,000、50,000、200,000和500,000,失效概率和变异系数如表2所示。 表2 拉丁抽样法结果 两种方法的结果如图2所示。由图2可知,当抽样个数达到50,000时,拉丁超立方抽样方法所计算的失效概率已经趋于稳定,而使用传统舍选法抽样需要达到200,000时,失效概率才趋于稳定。采用蒙特卡罗进行可靠度分析时,要得到失效概率稳定值,传统舍选法抽样数量为拉丁超立方抽样数量的4倍,表明使用拉丁抽样方法可以大大减少抽样数量。 两类抽样方法所得到失效概率的变异系数差别显著,如图3所示。传统舍选法变异系数随着抽样数量的增加,减小缓慢,而拉丁超立方抽样法得到变异系数减小明显。随着抽样数量的增加,两类抽样方法所得变异系数的比值由1.0,增加到2.0以上。对于达到同样的变异系数,需要的样本数量差别悬殊,例如当抽样数量为500,000时,变异系数为8.0%,而拉丁超立方法的样本数量50,000时,达到了相同的变异系数。这表明,达到相同的变异系数,拉丁超立方抽样数量可以减小到样本数量的1/10。 图2 失效概率随抽样数量的变化 图3 变异系数随样本数量的变化 除了达到稳定失效概率时,两种抽样数量差别悬殊外,在配置为Intel酷睿双核i3-6100台式机上,计算时间有很大的差异。以抽样数量为5,000 为例,计算过程表明,传统舍选法所用的时间约为65.17 s,而拉丁超立方抽样方法计算所用的时间为2 s,这表明在相同抽样数量的情况下,拉丁超立方抽样方法计算所用的时间要远小于传统舍选法。 传统舍选法计算的失效概率为0.35%,而拉丁超立方抽样方法为0.32%,两种方法的结果差异,是由于舍选法中土的粘聚力和内摩擦角被认为是二元正态分布的随机变量,而拉丁超立方抽样法中,假设粘聚力和内摩擦角相互独立,这是导致两者结果略有差异的原因。 (1) 采用蒙特卡罗法计算工程的失效概率时,拉丁超立方法得到失效概率所需要抽样数量显著小于传统舍选法所需的抽样数量,需要的样本数量约为舍选法数量的25%。 (2) 拉丁超立方法通过增加样本数量能够更有效减小失效概率的变异系数,相同抽样数量时其失效概率变异系数小于舍选法所得结果的一半。2.2 拉丁超立方法
3 抽样方法的对比
3.1 条形基础极限承载力计算
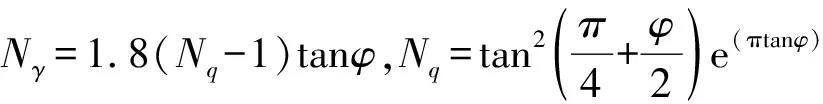

3.2 舍选法计算
3.3 拉丁超立方法计算
3.4 结果对比分析

4 结论

