基于神经网络模型的砾性土液化预测

邢明源，胡欣宇

(华北科技学院，北京 东燕郊 065201)

0 引言

地震诱发土的液化，会对房屋建筑、交通设施、水利设施等造成严重的破坏，给社会经济和人类生命安全都造成巨大的危害，因此土的液化问题一直受到学者们的关注[1,2]。地震诱发液化的判别是地震灾害研究的重要方向。对于地震中土液化判别问题，在1971年Seed和Idriss[1]、Whitman[2]提出了简化法，目前仍然是常用的液化判别方法。后来，剪切波速法[3,4]、标准贯入法(SPT)[5-7]和静力触探法(CPT)[8,9]相继提出，并在实践中得到广泛应用。

袁晓铭等[10]根据汶川地震实测数据，定义了砾性土是指由卵石、砾、砂、粉粒、黏粒等部分或全部组成的砾粒含量从 0～100%的宽级配土，是砾质土、砾砂、粉砾土、砂砾土和砾类土的的统称。以往普遍认为砾性土由于粒径较大、孔隙水压力消散较快，不会发生液化现象。自2008年汶川地震出现了大量的砾性土液化以来，砾性土液化问题逐渐受到国内外学者的关注。对于砾性土的液化判别，鉴于贝克贯入法(BPT) 需要复杂的试验技术和设备，基于汶川大地震现场试验和震害调查数据，Yuan等[11]和曹振中等[12]提出了动力触探法(DPT)方法，该方法在国际上具有推广的可行性。

近年来，随着人工智能快速发展，应用神经网络进行灾害预测预测受到了诸多学者们的重视。徐秀华[13]为了快速准确判别透水水源,从标准水样的水化学特征中提取出特征离子，建立了基于BP神经网络的煤矿透水水源判别法，得到了较好的判别结果，为煤矿水害防治提供依据；李方明和陈国兴[14]指出利用神经网络预测砂土液化的准确率与输入变量的不同组合及隐藏节点数目有关，但并没有具体指出输入变量的不同组合及隐藏节点数目与准确率的确切关系；陈榕等[15]以唐山地震中的轻亚黏土液化数据为样本，利用AFSs-RBF神经网络模型对液化危害等级进行预测划分得到了较好预测结果，却未考虑神经网络结构对预测准确率的影响；杜星等[16]利用多层感知(MLP)神经网络对地震作用下的砂土液化进行预测，并分析隐藏层和输入参数对准确率的影响，缺乏不同神经网络对预测准确的影响；毛志勇等[17]以唐山地震砂土液化现场勘察资料为样本，通过训练建立了结合遗传算法、支持向量机和Adaboost迭代算法的液化预测模型，预测结果表明新建立的模型具有更好的砂土液化预测准确性；康飞等[18]利用汶川地震液化资料，尝试对砾性土液化进行了神经网络预测，指出神经网络可以较好的预测砾性土的液化，但并没有讨论神经网络类型和隐藏节点数目对预测结果的影响。

由于砾性土液化实测数据有限，而液化机理并不完全清楚，为了快速对砾性土是否液化做出预测，为地震液化灾害防治提供依据，本文以汶川地震砾性土液化实测数据为样本，分别采用多层感知(MLP)和径向基函数(RBF)两种神经网络模型，预测砾性土的液化，对比两种模型中隐藏层节点数目和液化评价6个指标对预测准确率的影响。

1 神经网络

人工神经网络是一种典型的有监督机器学习算法，通过模仿自然界生物神经元之间电信号的传递，并由大量节点之间相互连接组成[16]。典型的前馈型人工神经网络由输入层、隐藏层和输出层构成，如图1所示。输入层的节点数由输入参数个数决定；隐藏层用来传递和处理信号，由相应的函数构成；输出层得出的是所需要的结果。

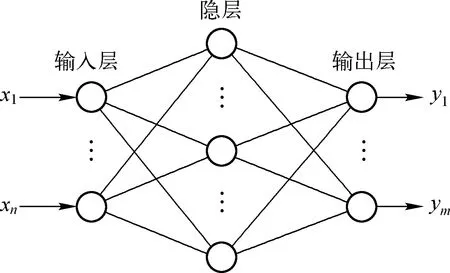
图1 前馈型神经网络结构

前馈神经网络的数学表达为

(1)

式中，x为输入参数；ωih为输入层-隐藏层权重；ωho为隐藏层-输出层权重；bih和bho为偏差参数；N为隐藏层节点数；M为输出层节点数；Tr(z)为传递函数，其中，

(2)

神经网络需要先对样本进行一系列的训练，减少训练值与实际结果的误差E：

(3)

式中，n为神经网络的训练样本个数；m为输出单元总个数；Ok为样本的k单元目标输出值；tk为样本的k单元实际输出值。

目前常用的两类前馈型人工神经网络模型分别是多层感知(MLP)、径向基函数(RBF)。多层感知(MLP)和径向基函数(RBF)神经网络相比，MLP神经网络具有1或2层隐藏层，而RBF神经网络只有1层隐藏层；MLP神经网络采用全局逼近，而RBF神经网络为局部逼近。

2 砾性土液化判别的神经网络模型

2.1 样本数据

影响土体液化的因素主要包括土层基本特性、地下水位和土层埋深、地震因素，同时剪切波速可以综合反映土体力学性能[18]。因此本文选取地震烈度SI、地震峰值加速度PGA、砂砾层深度ds、地下水位dw、有效上覆应力σv、剪切波速Vs共6个参数，作为液化的评价指标。砾性土液化样本取自于2008年四川汶川地震后曹振中等[19]的现场测量数据，共45组，如表1所示。根据汶川地震中砾性土地震液化样本参数，进行整理和统计计算，如表2所示。

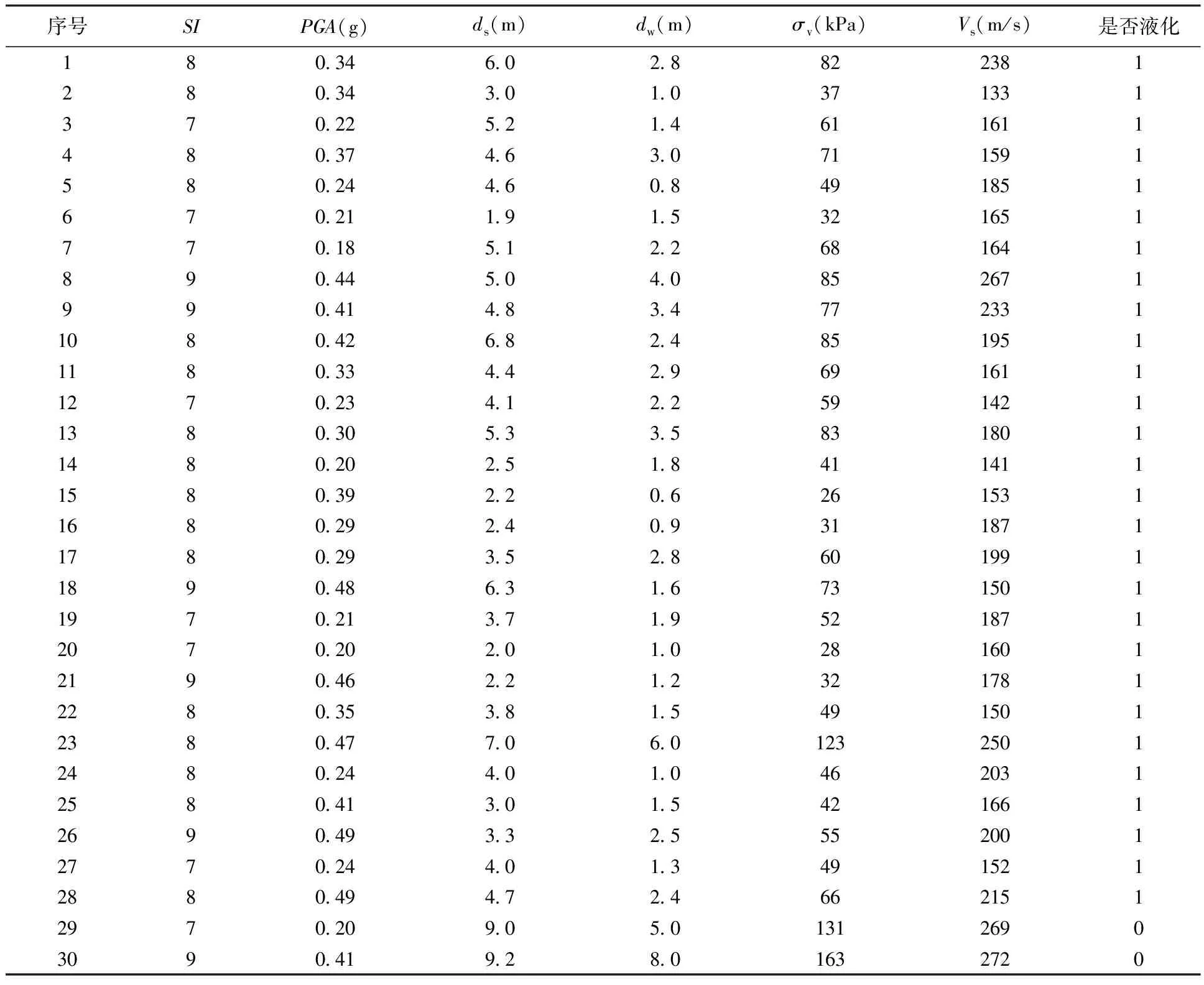
表1 砾性土液化数据

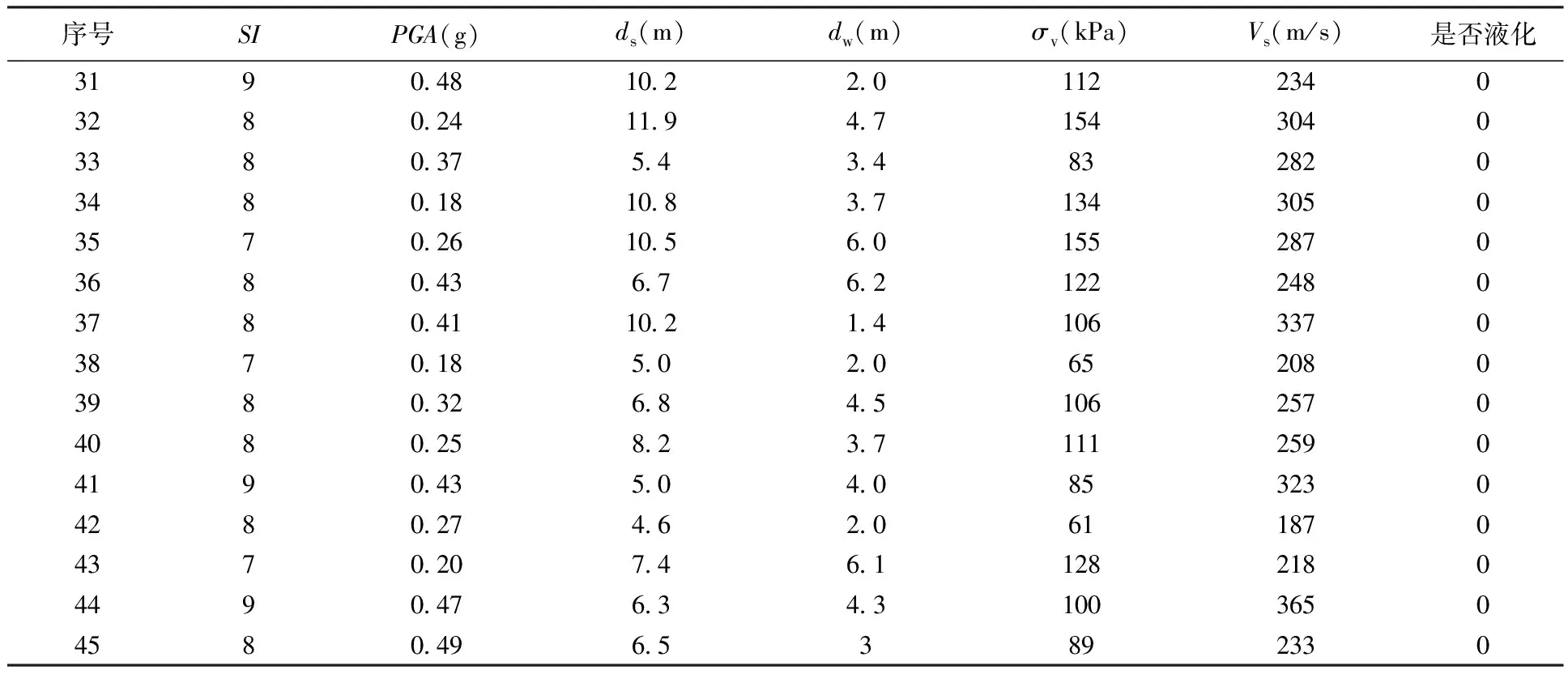
续表

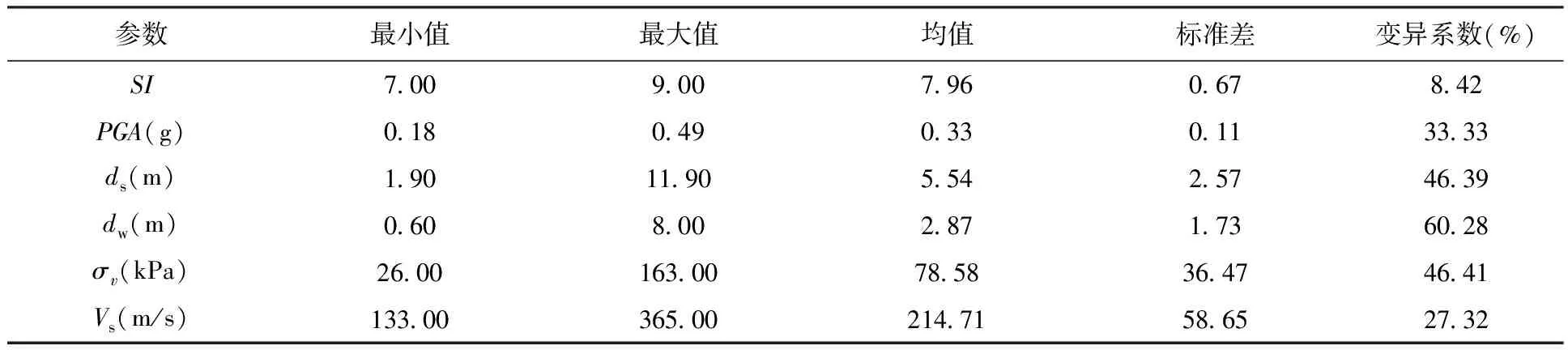
表2 地震砾性土液化参数描述统计

2.2 模型建立

将样本数据标准化处理后，采用以下步骤分别建立多层感知(MLP)和径向基函数(RBF)两类模型。

(1) 数据分割。随机选取数据总体的70%作为训练样本，剩余30%作为检测样本。

(2) 输入层确定。输入层节点数等于所选取的6个评价指标数目，即输入层的节点数目n为6。

(3) 隐藏层确定。为了比较，MLP和RBF模型的隐藏层都选1层。隐藏层节点数对神经网络的准确率非常重要，最佳的隐藏层节点数目在2n(n为输入节点数)节点附近[17]。为了分析隐藏层节点数目对预测精度的影响，两种模型的节点数目取值4～25，涵盖了最佳的2n值。

(4) 输出层确定。因为最终预测的结果为1或0，分别表示液化和未液化，所以输出层节点数目为1个。

3 液化预测结果与分析

3.1 模型预测结果

对于某一个神经网络模型，每一次的预测结果往往可能不同。为了对比MLP、RBF两类神经网络和隐藏节点数目对液化预测结果准确性的影响，计算中两种神经网络的每一种隐藏层节点数目均进行了50次预测， 两类神经网络模型的预测结果包括平均准确率、中位准确率、最差准确率和最佳准确率，如图2所示。图2表明，当隐藏节点数大于10时，RBF神经网络模型预测结果的平均准确率、中位准确率和最佳准确率，明显高于MLP预测结果，而两种模型预测结果的最差准确率相差不大，但MLP预测结果波动相对较大。

3.2 节点数目影响

图2(a)和2(b)表明，随着隐藏节点数的增多，MLP网络预测结果的平均准确率和中位准确率低于RBF网络预测结果。当节点数目为10时，RBF网络的平均准确率和中位准确率超过了MLP网络，随后RBF网络的预测性能已经高于MLP网络；在节点数为17时，RBF网络的平均准确率出现最大值92.96%。图2(d)表明，随着隐藏节点数的增加，两种网络都达到了准确率的最大值，RBF网络的最佳准确率达到100%，而MLP网络的最佳准确率达到98%。这表明，RBF和MLP两种网络模型都有较好的预测能力，并且都随着隐藏节点数变化而改变，但RBF网络对隐藏节点数的变化更为敏感，当隐藏节点数增加时，RBF网络预测性能明显优于MLP网络。

图2 RBF与MLP预测结果

3.3 输入参数影响

为了研究所选取的6个指标对神经网络预测准确率的影响，选用预测能力较好的RBF神经网络模型，其中隐藏节点数为17，相应的平均准确率为92.96%。分为6种工况，在每种工况中分别忽略某一个指标，然后再进行50次预测，从而得到本组预测的平均准确率，预测结果如表3所示。

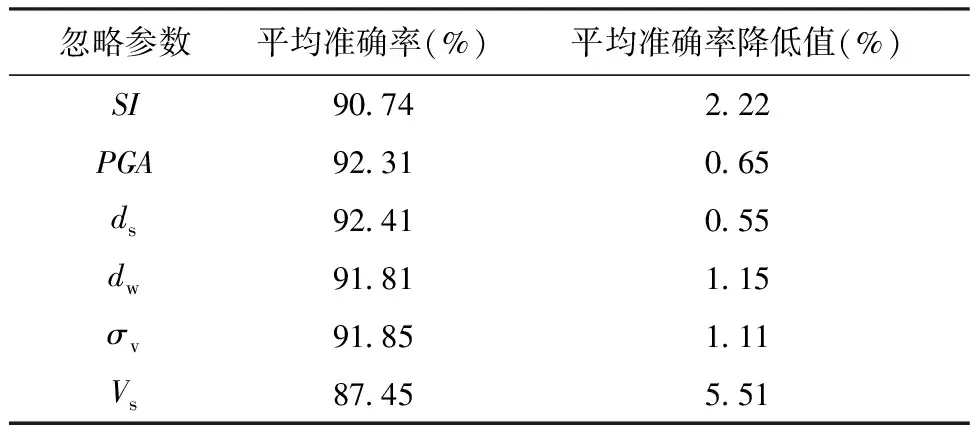
表3 输入参数对预测结果的影响

对比6种工况的平均准确率与考虑所有指标相应的平均准确率92.96%，得到相应的平均准确率降低量。计算结果表明，当忽略剪切波速Vs时预测准确率降低最多，达到5.51%，说明剪切波速Vs是预测地震作用下砾性土液化的最重要参数；而忽略砂砾层埋深ds和地震峰值加速度PGA时，对神经网络预测模型的平均准确率并没有太大影响。对影响神经网络预测结果准确性的指标排序，由高到低依次为剪切波速Vs、地震烈度SI、地下水位dw、有效上覆应力σv、地震峰值加速度PGA和砂砾层深度ds。

4 结论

(1) 神经网络模型MLP和RBF对砾性土的液化都有较好的预测能力，当隐藏节点数目超过10时，RBF网络模型整体优于MLP网络模型， RBF最佳准确率达到100%。

(2) RBF网络模型对隐藏节点数目比较敏感，其平均准确率随着隐藏节点数增加而提高，当节点数为超过13时，平均准确率约为92.00%，当17时，平均准确率达到最大值92.96%。

(3) 利用隐藏节点数为17的RBF神经网络模型，分析了6个指标对影响神经网络预测结果准确性的排序，由高到低依次为剪切波速、地震烈度、地下水位、有效上覆应力、地震峰值加速度和砂砾层深度。