高碳钢丝多道次拉拔及矫直对残余应力的影响

蔡 磊，朱建国，程 亮,，张帅今，唐 斌

(1. 盛利维尔(中国)新材料技术股份有限公司，江苏 常州 213000)(2. 江苏理工学院材料工程学院，江苏 常州 213001)(3. 西北工业大学 凝固技术国家重点实验室，陕西 西安 710072)

1 前 言

冷拉拔高碳珠光体钢丝具有极高的强度，是目前强度最高的钢铁制品[1]。由于其优异的力学性能，拉拔钢丝被广泛用作轮胎帘线、焊丝、弹簧及切割丝等，在工业生产中占据重要地位[1-3]。然而，受拉拔本身工艺特性及摩擦的影响，钢丝横截面的变形很不均匀，从而在成形后产生残余应力。残余应力的存在显著影响冷拔钢丝的疲劳寿命、屈服强度等一系列使用性能[2-4]，因此拉拔过程及后处理过程中残余应力的形成与演变行为受到国内外的广泛关注。

目前，研究钢丝残余应力的实验方法主要包括衍射法、切口法、钻孔法等[3]。受限于钢丝尺寸，其中切口法、钻孔法等破坏性测量法不适用于细丝；而无损测量如衍射法等只能检测钢丝表面的残余应力。利用X射线，Willemse等[5]及Yang等[6]采用逐层剥蚀的方式衍射测量出了钢丝从表层到心部的残余应力分布，然而这种方法效率低下且成本较高。随着计算机及数值分析技术的发展，采用弹塑性有限元理论分析钢丝拉拔过程中的残余应力演变逐渐成为一种有力手段。基于Ansys、Abaqus、Deform-3D等有限元数值仿真平台[7-9]，人们能够方便、快速地对拉拔成形过程中的多物理场进行全过程追踪，从而揭示拉拔成形过程中残余应力的形成和演变规律。数值仿真已经成为研究钢丝拉拔成形规律的主要手段之一，然而目前针对残余应力的研究主要集中在单道次拉拔，对于中间道次的残余应力演化以及后续矫直过程对残余应力的影响还需进一步研究[4]。因此，本研究针对T9高碳钢在多道次拉拔过程及后续拉伸矫直过程中的残余应力演变进行研究，进而揭示拉拔道次及拉伸矫直对残余应力的影响，为拉拔工艺优化及钢丝性能提升提供理论借鉴。

2 实验方法及有限元模型

本研究所使用的拉拔材料为正火态的T9高碳钢盘条，其初始直径为1.8 mm。经8个道次拉拔后直径变为0.9 mm，每道次平均压缩率约为16%。拉拔所采用的模具为金刚石拉丝模，半模角为5°，定径带长度为钢丝直径的0.3倍。为了获得每道次变形对钢丝力学性能的影响，同时为数值模拟提供材料模型，对不同道次拉拔后的钢丝进行了拉伸实验，获得的应力应变曲线如图1所示。由图1可以看出，随着变形道次的累积，钢丝发生加工硬化，其抗拉强度逐渐提升。

基于Abaqus有限元数值仿真平台建立了钢丝拉拔模型。为了减小网格规模、简化计算过程，采用轴对称的方式建模，如图2所示。其中拉丝模约束为刚体，忽略其变形；钢丝则采用弹塑性CAX4R单元进行离散。为了避免局部效应同时减小网格规模，钢丝的初始长度设置为20 mm。考虑到钢丝表层的轴向剪切效应较为显著，采用表层密、心部疏的梯度化网格以提高模拟结果的准确性。根据图1所示的拉伸实验结果，钢丝盘条的弹性模量为210 GPa，屈服强度为825 MPa，硬化曲线按照图1中不同道次的拉伸数据进行插值、优化后获得，如图1中粗线所示。由于在实际拉拔过程中，钢丝与拉丝模之间充分润滑，且循环流动的润滑液能够及时带走热量，因此在进行拉拔模拟时将钢丝视为率无关材料，忽略其变形产热效应。

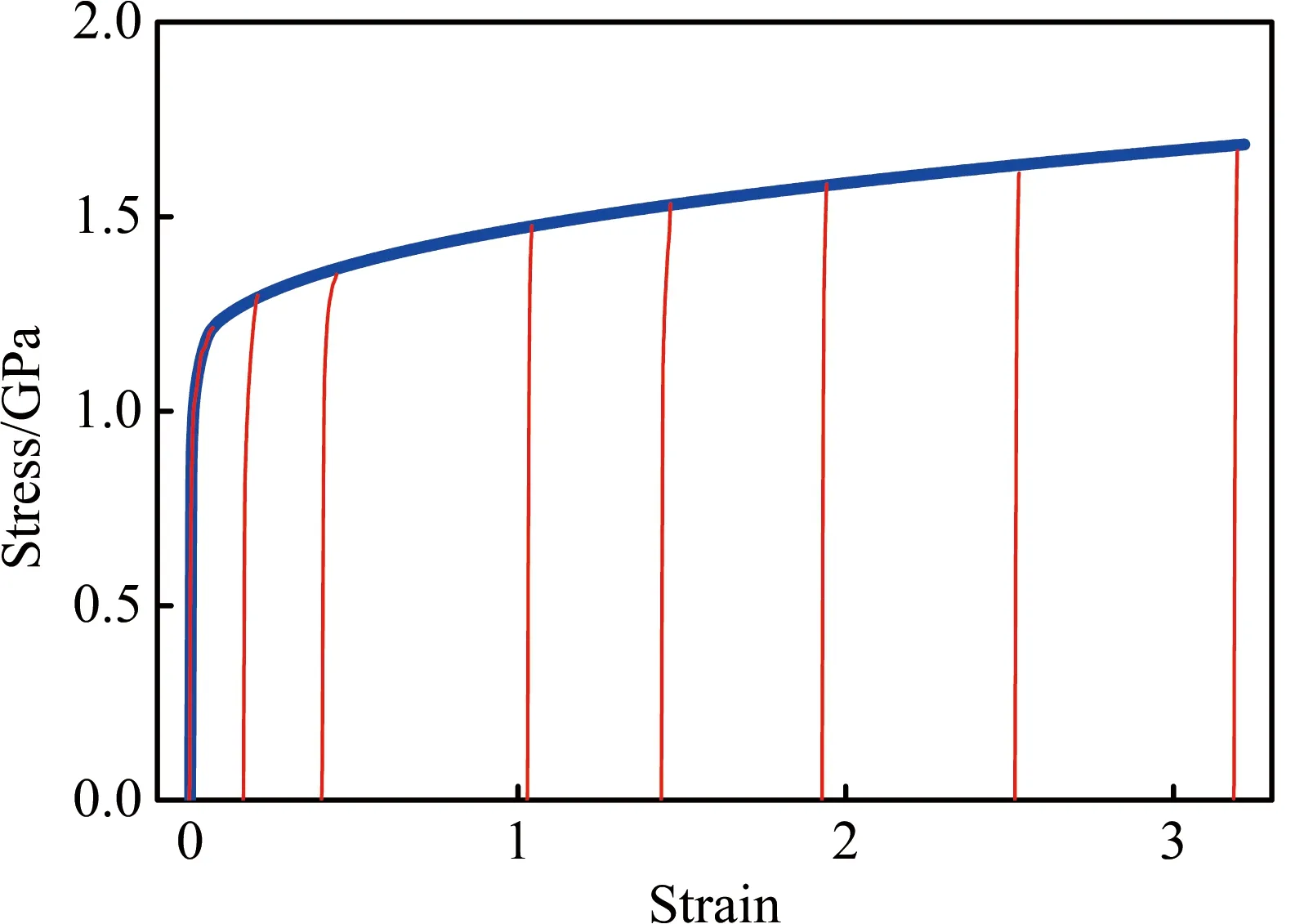
图1 拉拔钢丝的应力应变曲线。其中细实线为各道次拉拔后钢丝实测应力应变曲线，粗实线为插值获得的完整应力应变曲线Fig.1 Tensile stress-strain curves of the steel wire. The thin lines are the measured stress-strain curves after various drawing-passes, the thick line is the stress-strain curve obtained by interpolation

图2 钢丝拉拔有限元模型(a)，变形区的放大图(b)Fig.2 Numerical model for the steel wire drawing(a), the enlarged map of the deformed region(b)

为了验证数值模型的可靠性，本研究将经8道次拉拔后的钢丝进行单向拉伸模拟，并将获得的应力应变曲线与实验数据进行对比，结果如图3所示。可以看到，预测的钢丝拉伸应力应变曲线与实测曲线几乎完全吻合。此外，预测的钢丝均匀延伸率约为1.2%，随后产生颈缩。由于模型并未考虑断裂，因此不能直观地预测其断裂延伸率。然而无论是实际的应力应变曲线(图3)还是文献[1]中的断口照片，均表明高碳钢丝在单向拉伸时的应力应变曲线无显著降低、几乎不产生颈缩，即断裂延伸率约等于均匀延伸率。由此可知，经8道次拉拔后，采用所建立的数值模型预测的钢丝延伸率约为1.2%。而实测钢丝延伸率为1.1%，两者几乎一致。通过以上对比说明所建立的数值模型可靠程度高、模拟结果准确性好。

图3 经8道次拉拔后钢丝的应力应变曲线Fig.3 Tensile stress-strain curves of the steel wire after 8 drawing-passes

3 结果与讨论

3.1 残余应力分布特征

拉拔钢丝在径向、轴向和切向3个方向上均存在残余应力，其中轴向残余应力最为突出，因此也最受关注[10]。为了分析拉拔后轴向残余应力的分布特征，对经第一道次拉拔后的钢丝取中间横截面的径向路径进行分析，获得从中心到边缘的节点残余应力值，如图4所示。由图中可以看出钢丝经拉拔后，心部的轴向残余应力为压应力，且绝对值非常大；随着向表层靠近，轴向应力的绝对值逐渐减小，并在相对位置约0.65处变为0，然后转变为拉应力并逐渐提高，在表层一定深度内达到最大值且随后不再显著变化。这种变化规律与其他文献中用衍射法获得的实测变化规律保持一致[2]，从而再次验证了模拟结果的有效性。

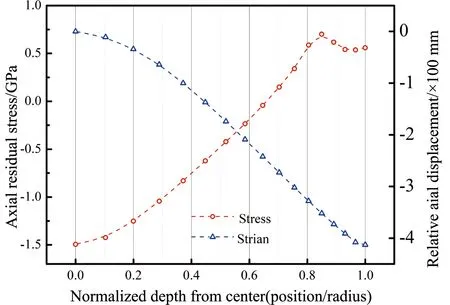
图4 第一道次拉拔结束后钢丝的轴向残余应力及横截面的轴向相对位移分布Fig.4 Distribution of the axial residual stress and relative axial displacement of the cross-section of the steel wire after the first drawing-pass

钢丝的轴向残余应力主要是由于表层和心部金属流动速度的差异所导致的。影响拉拔过程中金属流动速度的因素主要有两点，一是钢丝表面与拉丝模之间的摩擦阻碍了表层金属的流动，二是锥形的模孔使钢丝表层材料的移动距离加长。在这两种因素的作用下，钢丝表层的轴向流动速度滞后于心部。为了保持钢丝的整体性，心部区域必然为表层施加额外的附加拉应力以促进其流过模孔。相应地，钢丝心部则受到附加压应力作用。由此可知，轴向残余应力的产生是钢丝横截面流动速度不均匀的结果，因而其性质和分布规律可以用变形后横截面的相对移动进行解释：

Si=Ui-U1

(1)

其中，Si为径向路径上第i个节点相对于中心节点的轴向相对位移，Ui为第i个节点的轴向位移，U1为中心节点的轴向位移。径向路径节点的相对位移如图4所示，可以明显看到，越接近表层，节点的相对位移的绝对值越大，其流动越滞后于心部，整体上呈反S型分布，恰好与轴向残余应力的正S型分布相对应，从而解释了钢丝外正内负的轴向残余应力分布特征。

3.2 拉拔道次对残余应力的影响

拉拔道次对轴向残余应力的影响如图5所示。可以看到，随着拉拔道次的增加，钢丝心部的残余压应力有所提高，表层的残余拉应力也略微增大，说明拉拔道次在一定程度上增加了残余应力的不均匀性，然而其影响并不显著。根据前面的分析可知，轴向残余应力的大小取决于钢丝在穿过模孔时横截面各个部位的相对流动速度，而与变形量的绝对值无关。因此，钢丝在第一道次拉拔后即确立了残余应力的分布特征。在后续拉拔道次中，由于变形条件与第一道次相差不大，钢丝在穿过模孔时不同道次之间表层与心部的速度差变化不明显，因此钢丝维持了第一道次的残余应力分布规律。总而言之，随着拉拔道次的增加，虽然累积变形量显著提高，但仅略微加剧了轴向残余应力分布的不均匀性，整体而言残余应力的变化不显著。

图5 不同道次拉拔后钢丝横截面的轴向残余应力分布Fig.5 Distribution of the axial residual stress of the cross-section of the steel wire after various drawing-passes

3.3 拉伸矫直对残余应力的影响

拉拔钢丝在成品前往往需要经过一道矫直工序。矫直的本质是引入少量的塑性变形以改善钢丝内部的应力分布，从而使弯曲的钢丝变直。为了研究少量塑性变形对钢丝残余应力的影响，本研究将经8道次拉拔后的钢丝分别施加0.2%～1%的拉伸变形量后卸载，分析少量轴向变形对残余应力的影响。

在无残余应力的前提下，当钢丝承受单轴拉应力时各个部位将均匀变形，即横截面上各个节点的轴向运动保持同步。而当存在残余应力时，各节点可能由于变形抗力的不同而造成轴向移动不同步。如前所述，各节点之间相对位移的大小直接关系到轴向残余应力的分布。因此，为了定量分析拉伸加载过程中钢丝横截面上各节点的轴向移动情况，本研究引入相对位移差这一变量，其表达式为：

(2)

图6为不同拉伸变形量下钢丝横截面节点的相对位移差，可以看到在残余应力的作用下，钢丝在伸长过程中横截面的移动是不同步的，表层的相对位移量大于心部，而且随着拉伸变形量的增大，钢丝表层的相对位移差显著增大。这主要是由于钢丝在矫直前的残余应力为内负外正，当钢丝在矫直过程中承受拉应力时，在应力叠加的作用下钢丝表层的拉应力进一步提高，从而使表层区域更容易发生轴向伸长。这种变形的不同步也能够从图7所示的屈服范围云图中得以体现。可以明显看到，随着拉伸的进行，钢丝残余拉应力最大的区域(亚表层)先发生屈服并逐渐扩展至整个表层拉应力区，然后再逐步向心部压应力区扩展。

图6 不同拉伸变形量下钢丝横截面节点的相对位移差Fig.6 Relative displacement error of the cross-section of the steel wire at various tensile deformation

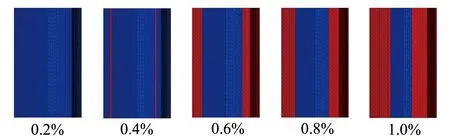
图7 不同拉伸量下钢丝屈服范围的变化，红色区域为屈服区，蓝色区域为未屈服区Fig.7 Evolution of the yield area at various tensile elongations, the red regions denote the yield area while the blue regions are the area that has not yield

前文指出，在拉拔过程中钢丝表层的流速小于心部，从而造成内负外正的轴向残余应力分布；而在拉伸矫直过程中材料流动则表现出相反的趋势，表层流速较快而心部较慢。可想而知，通过这种流速补偿，拉伸矫直可能能够有效改善钢丝的轴向残余应力。为了验证这一点，本研究对拉伸—卸载后钢丝的轴向残余应力分布进行了分析，如图8所示。可以看到，当拉伸变形量小于0.4%时，与初始状态相比残余应力几乎没有任何变化。这主要是由于变形量较小，不足以引起钢丝显著的塑性变形所致(图7)。随着拉伸量的进一步提高，最大压应力和拉应力均开始降低，且降低幅度越来越大，残余应力的分布均匀性得到了显著改善。

图8 拉伸变形量对轴向残余应力分布的影响Fig.8 Effect of tensile deformation on the distribution of axial residual stress

由此可见，给与拉拔钢丝一定的轴向拉伸是改善其残余应力分布的有效手段，而且拉伸变形越大效果越显著。然而，值得注意的是，钢丝经8道次拉拔后的延伸率仅为1.1%，因此拉伸矫直量应控制在1%以下，避免钢丝在矫直过程中发生断裂。

4 结 论

本研究主要对T9高碳珠光体钢丝在多道次拉拔及后续拉伸矫直过程中的轴向残余应力进行分析，所得主要结论如下：

(1)根据实际的钢丝拉拔过程建立了有限元数值模型，并结合实验结果验证了模型的有效性。数值仿真的结果表明，钢丝经拉拔后表层为拉应力，心部为压应力。拉拔道次的提高对轴向残余应力的影响较小。

(2)拉伸矫直能够显著改善轴向残余应力的分布规律。随着拉伸变形量的提高，残余应力最大值显著降低，残余应力分布更加均匀。然而，拉伸变形量的上限取决于钢丝的延伸率，过大的拉伸矫直量会使钢丝发生断裂。