4线车站浅埋隧道施工过程中锚杆受力特性研究

卿伟宸，朱 勇，章慧健

(1.中铁二院工程集团有限责任公司，四川 成都 610031；2.西南交通大学，四川 成都 610031)

0 引言

锚杆是一种优化的隧道围岩支护形式[1]，自1872年首批锚杆在英国投入使用[2]，一个多世纪以来，锚杆支护作为重要的支护方式，已广泛应用于公路、铁路隧道施工[3-4]，在加固围岩和提高围岩的自承能力方面发挥着重要作用。

目前，关于锚杆支护理论及作用机制等研究[5-8]以及在大跨度隧道初期支护锚杆受力特性的研究方面已有不少成果，例如：王丙兴[9]依托邢汾高速公路某隧道，采用现场监测的手段对锚杆的受力状态进行监测分析；周丁恒等[10]以广州龙头山双洞8车道公路隧道为背景，对不同施工工序下隧道支护体系力学性能进行监测与分析；陈远志等[11]依托某3车道公路隧道，对非均质围岩地段锚杆应力进行了监测分析；王应富等[12]基于广州东二环高速公路某4车道公路隧道，采用有限元法对大跨度隧道整个开挖过程进行了动态模拟研究，对锚杆轴力的动态变化特性进行了分析；陈耕野等[13]依托沈大高速韩家岭4车道隧道，对大跨度隧道锚杆内力随时间的变化进行了监测及分析。

以往的研究主要是针对系统锚杆沿隧道拱墙范围均衡支护(等间距、等长度设置)的情况，对于大跨大断面隧道，初期支护系统锚杆用量相对较多，若还是按最不利部位采用等参数设置，势必产生浪费，增加施工成本。采用系统锚杆不等参支护可实现结构安全可靠、设计合理、节省投资的目的[14]。目前关于系统锚杆不均衡支护的研究较少，且主要集中在双连拱隧道及倾斜层状岩体隧道，例如：文献[15-16]对双连拱偏压隧道受力特性进行了研究，提出了支护结构非对称设计方法，即受力较不利的一侧适当加强支护，受力较好的一侧适当减弱支护；任耀文[17]研究认为,陡倾小交角层状岩体隧道顺倾侧和反倾侧破坏模式呈现出明显的非对称性，采用不对称支护是很有必要的。

随着我国高标准铁路的快速发展，尤其在西部山区，受地形条件及曲线半径等限制，大量车站需伸入隧道，传统的大跨大断面3线隧道已不能满足山区选线及设站的需要，类似于六(盘水)沾(益)铁路乌蒙山2号4线车站隧道的大跨大断面4线隧道将越来越多。为深入了解大跨大断面车站隧道锚杆受力变化特征及各部位最终受力状态，为建立特大跨度隧道不等参支护设计提供参考，本文依托乌蒙山2号4线车站隧道浅埋段工程实例，利用数值模拟方法，分析不同部位锚杆轴力特征，并结合现场锚杆受力监测情况，研究4线车站大跨大断面浅埋隧道不同部位锚杆受力特性的差异，提出锚杆不等参支护建议参数。

1 工程概况

六盘水至沾益铁路，设计时速160 km，开行双层集装箱。乌蒙山2号隧道为该线第一长隧，亦为该线的控制性工程，隧道全长12 260 m，由观音河右岸进洞，止于扒挪块车站，最大埋深400余m。

根据运能要求，隧道出口段扒挪块车站伸入隧道，DK287+740～DK288+350段形成4线车站隧道，长610 m，最大开挖宽度达28.42 m，最大开挖面积为354.30 m2，是国内首座4线铁路车站隧道。

洞口DK288+240～+350段110 m为浅埋段，埋深不超过50 m。该段洞身通过以泥岩、页岩夹砂岩为主的Ⅴ级软岩地层，采用复合双侧壁“撑索转换”工法施工，工法及支护示意如图1所示。

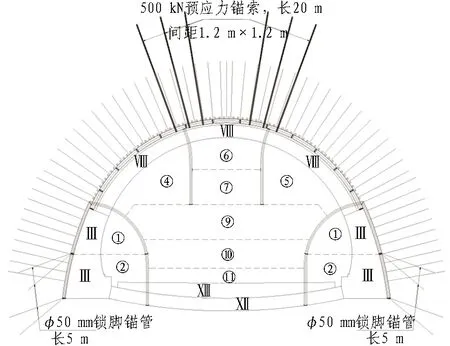
①、②分别代表两侧下导洞的上、下台阶；④、⑤分别代表拱部左、右侧导洞；⑥、⑦分别代表拱部核心土上、下台阶；⑨、⑩、分别代表下部核心土上、中、下台阶；Ⅲ代表左右侧边墙；Ⅷ代表拱部二次衬砌；Ⅻ代表仰拱；代表仰拱填充。图1 洞口浅埋段工法及支护Fig.1 Construction method and support structure of shallow-buried portal section

2 等参支护锚杆受力特征

2.1 锚杆现场施工要求

本工程中，锚杆采用组合中空注浆锚杆。在初喷混凝土后，方可钻设锚杆孔。钻孔前先清理钻头，钻孔完成后，将安装好锚头和止浆塞的组合中空注浆锚杆插入孔中，保持锚杆的外露长度为10～15 cm。锚杆注浆材料采用水灰质量比为1∶1的组合中空注浆锚杆，水胶质量比为0.4～0.5，砂子粒径不大于1.0 m。注浆按以下程序进行：首先，迅速将锚杆、注浆管及注浆泵用快速接头连接好；然后，开动注浆泵注浆，直至浆液从止浆塞上的排气孔溢出或压力表达到设计压力值为止，且每根锚杆注浆必须“一气呵成”。一根锚杆注浆完成后，应迅速卸下注浆软管和锚杆接头，清洗后移至下一根锚杆使用。若停泵时间较长，则在下一根锚杆注浆前要放掉注浆管内残留的灰浆；注浆过程中，每次移位前应及时快速清洗接头，以保证注浆连续进行。锚杆施作完毕强度达到10 MPa后，即可安设锚杆垫板(垫板尺寸为150 mm×150 mm×6 mm)，并上螺帽。

组合中空注浆锚杆饱满度质量采用声波检测仪测定，检测原理是：在锚杆体外端用声波震源激发高能脉冲声波，声波沿杆体钢筋以管道波形式传播，到达钢筋底部后反射回波被接收。若组合中空注浆锚杆填充密实，则超声波在传播过程中能量损失很大，在杆体外测得的反射波振幅小；反之亦然。最后以接收到反射波的反射时间、波幅、频率、相位等参数，判断锚杆的长度及组合中空注浆锚杆的密实程度。

2.2 现场监测

监控量测是隧道工程设计、施工过程中重要的环节，是反映隧道结构安全性的最直接方式[18-19]，是实现动态施工的基础[20]。为监测本工程中锚杆受力特征，并验证理论计算结果，选取DK288+287断面，分别在拱顶、拱肩、边墙上部及下部选取典型锚杆，按规范[21]对锚杆内力进行监测。各部位监测锚杆编号如图2所示。“MZ”表示锚杆轴力测点，共计7套锚杆计。监测得到的各部位锚杆在施工过程中的轴力变化如图3所示。各部位锚杆最终受力情况如图4所示。由图3可以看出，除拱顶锚杆轴力持续较小外，其余部位锚杆轴力总体上初期增长较快，而后逐渐趋于稳定并略有波动。

图2 各部位监测锚杆编号Fig.2 Number of monitoring anchor bolts

(a)MZ1锚杆(拱顶)

图4 锚杆实测轴力分布图(单位：kN)Fig.4 Axial force distribution of systematic anchor bolt (unit:kN)

由图3和图4分析可知，现场实测锚杆受力具有以下特点。

1)锚杆终态受力基本为锚杆轴力最大值。

2)拱顶锚杆受力最小，最大轴力仅为3.9 kN；边墙上部锚杆受力最大，最大轴力值为48.1 kN。各部位监测锚杆受力大小关系表现为边墙部位>拱肩部位>拱顶部位。

3)左右两侧对称部位的锚杆最大轴力差异较小。边墙下部左侧锚杆最大轴力值为17.4 kN，右侧锚杆最大轴力值为21.4 kN，偏差值约为18.7%；边墙上部左侧锚杆最大轴力值为44.1 kN，右侧锚杆最大轴力值为48.1 kN，偏差值约为8.3%；拱肩部位左侧锚杆最大轴力值为37.4 kN，右侧锚杆最大轴力值为31.5 kN，偏差值约为15.8%。

2.3 数值模拟计算

2.3.1 计算模型及参数

由于浅埋段地应力受地表坡度影响较大，计算中采用FLAC3D建立三维模型，地表坡度按1∶1建模，计算范围左右各取100 m，仰拱下取为60 m。前、后、左、右边界施加相应方向的水平约束，下边界为竖向约束，上边界为自由面。初始应力仅考虑自重应力场的影响。地层采用服从Mohr-Coulomb屈服准则的弹塑性本构模型，喷射混凝土采用壳单元模拟。钢架的作用按等效方法予以考虑，即将钢架弹性模量折算给喷射混凝土，其计算如下：

(1)

式中：E为折算后的混凝土弹性模量；E0为原混凝土弹性模量；Sg为钢架截面积；Eg为钢材弹性模量；Sc为混凝土截面积。

建立的计算模型及网格划分示意如图5所示。支护参数如表1所示，围岩物理力学参数如表2所示，锚杆物理力学参数如表3所示，支护结构物理力学参数如表4所示。

(a) (b)图5 计算模型及网格划分示意图Fig.5 Diagram of calculation model and meshing

表1 支护参数Table 1 Support parameters

表2 围岩物理力学参数Table 2 Physico-mechanical parameters of surrounding rock

表3 锚杆物理力学参数Table 3 Physico-mechanical parameters of anchor bolt

表4 支护结构物理力学参数Table 4 Physico-mechanical parameters of support structure

2.3.2 数值计算结果

经过数值模拟计算，选取如图6所示的10根典型锚杆，提取每根锚杆在每一分部开挖后的轴力，并绘制其变化曲线图，结果如图7所示。

图6 锚杆编号Fig.6 Number of anchor bolts

图7 锚杆轴力变化曲线Fig.7 Change curves of axial force of anchor bolt

从图7中可以看出：1)各部锚杆施作后，轴力迅速增加，之后保持基本稳定。2)锚杆终态受力基本为锚杆轴力最大值。

为分析不同部位锚杆受力特性的差异，提取并整理拱墙范围内所有锚杆的最终轴力，具体见表5。锚杆轴力沿拱墙范围的分布示意如图8所示。

结合表5及图8可以得到如下结论：

1)不同部位锚杆轴力分布不一致且差异较大，大小分布表现为边墙部位>拱肩部位>拱顶部位。

2)从隧道左右两侧对称部位的锚杆轴力值对比来看，分部先后开挖引起同部位左右不对称的情况不明显，差值较小，具体表现为边墙部位锚杆轴力右侧略大于左侧，偏差值多数在5%以内；拱肩部位除局部几根锚杆外，左右侧偏差值在10%以内。

2.4 现场监测与数值计算结果对比分析

根据图4及图8，整理得到MZ1—MZ7位置锚杆现场监测结果及数值计算结果对比，结果见表6。

表5 锚杆轴力对比Table 5 Comparison of axial force of anchor bolt

图8 锚杆轴力沿拱墙范围的分布示意(单位：kN)Fig.8 Distribution of axial force of anchor bolt (unit:kN)

从表6可以看出，现场实测锚杆受力特点及规律与数值计算结果较为吻合。

表6 实测锚杆轴力及计算轴力对比Table 6 Comparison between measured and calculated axial force of anchor bolt kN

由表6可知：1)拱顶锚杆受力最小，边墙锚杆受力最大，各部位锚杆受力大小关系表现为边墙部位>拱肩部位>拱顶部位。2)左右两侧对称部位的锚杆最大轴力差异较小。

结合监测结果及计算结果分析可知，由于隧道开挖跨度大，拱部松弛范围大，拱部锚杆位于松弛区范围，不能发挥“悬吊”作用。因此，拱部锚杆轴力较小。但拱部锚杆与边墙锚杆一同发挥组合拱作用，使洞室周边围岩受径向压力作用而形成组合拱，从而提高岩体强度及围岩整体稳定性。因此，拱部锚杆不能取消，但在保证洞周锚杆形成组合拱效应的前提下，可以适当加大间距或减小长度。

3 锚杆不等参支护研究

根据第2节的研究分析结果，并基于“按需配置，充分发挥锚杆支护能力”的原则，对锚杆支护拟采取“不同部位不等参支护，左右对称部位等参支护”的方案，并进行数值模拟分析计算。

3.1 拱墙范围锚杆长度不等参研究

为研究拱墙范围不同部位对锚杆长度的需求响应情况，初步拟定如表7所示的5种锚杆不等长度布置工况(锚杆间距均按0.8 m×0.8 m布置)。通过计算分析，不同工况下的围岩位移(拱顶沉降、水平收敛)、塑性区面积及锚杆轴力对比如图9所示。

表7 5种锚杆不等长度布置工况Table 7 Five conditions of anchor bolts with different lengths

(a)不同工况下的拱顶沉降对比

1)从图9(a)与(b)可以看出，拱顶沉降及水平收敛随着锚杆长度的增加而减小，但随着锚杆长度的减小，减小幅度越来越小。锚杆长度超过工况3以后，继续增大锚杆长度对限制围岩位移的效果不明显，从节省投资角度来看是不经济的。

2)锚杆长度对塑性区的发展影响较大，且转折点较为明显。锚杆长度超过工况3以后，继续增大锚杆长度后，对塑性区的影响较小。

3)锚杆轴力与锚杆长度有关。根据锚杆受力的剪滞理论模型可以推测，锚杆的轴力等于锚杆与黏结材料接触面上的剪应力沿杆身方向的积分，锚杆越长，积分长度越长，轴力也越大。因此，对于锚杆轴力偏小的区域需谨慎换用短锚杆，锚杆越短，轴力越小，越不能充分发挥材料的支护强度，相应地围岩变形可能出现失控。从图9(d)可以看出，当锚杆长度超过一定值后，尽管轴力会继续增加，但增加的幅度已经开始减小，这是因为在积分长度增加的同时，积分变量(剪应力)在减小。总体上来看，5种工况中最大锚杆轴力为93.7 kN，约为设计值(150 kN)的62.5%，因此，锚杆轴力可以不作为控制因素。

综上，工况3是相对较为合理的锚杆长度布置工况，即边墙部位(①②部)取5 m，拱肩部位(④⑤部)取4 m，拱顶部位(⑥部)取3 m。施工图原设计拱墙范围锚杆长均为5 m，与之相比，采用工况3的布置形式每延米隧道可减少锚杆57.5 m。

3.2 拱墙范围锚杆间距不等参研究

改变锚杆刚度除了改变锚杆长度以外，还可以改变锚杆间距。为便于计算分析，在不改变锚杆长度及纵向间距的基础上，初步拟定如表8所示的5种不同锚杆环向间距布置工况(锚杆长度均采用5 m，纵向间距均为0.8 m)。

表8 5种锚杆不等间距布置工况Table 8 Five conditions of anchor bolts with different spacings

锚杆间距太大，各个锚杆的压缩区不能交叠，形成不了连续的压缩带；反之，间距太小会影响支护效果，易出现整体拔出破坏。即使未破坏，支护效果的增加与锚杆用量也是不匹配的，是不经济的。5种工况下的围岩位移(拱顶沉降、水平收敛)、塑性区面积及锚杆轴力对比如图10所示。

(a)不同工况下的拱顶沉降对比

由图10可以看出：

1)锚杆间距对围岩位移绝对值的影响很小。从工况1—5，随着锚杆间距的增大，拱顶沉降逐渐增加，并趋于平缓；水平收敛呈现先略有减小再增大的趋势，即工况1反而比工况2略大，这主要是因为锚杆间距始终在锚杆长度的1/2以内，可以形成连续压力拱；同时，间距变化引起锚杆的着力点不同，因此出现了在一定间距范围内锚杆间距大者变形反而小的情况。

2)锚杆间距对塑性区的影响较为明显，锚杆间距直接影响改善后的围岩强度。随着锚杆间距的减小，塑性区逐渐减小，但减小幅度越来越小。

3)锚杆轴力与锚杆间距的关系不明显，锚杆的位置(着力点)可能比间距更能影响其轴力大小。由于锚杆间距对围岩变形的影响是微弱的，从图10(d)可以看出，这几种工况的锚杆轴力分布基本是一致的，仅在边墙部位有较大波动，这与等参支护边墙部位锚杆轴力变化较大是一致的。

综上，工况2和工况3的锚杆间距布置是相对较为合理的布置形式。结合围岩位移、塑性区面积及锚杆轴力综合考虑，工况3最优，且支护作业所需时间短。施工图原设计拱墙范围锚杆采用等间距0.8 m设置，与之相比，采用工况3的布置形式每延米隧道可减少锚杆约112.5 m，节省约31%。

3.3 现场优化及监测情况

结合以上计算分析，并根据DK288+287断面锚杆受力监测情况，在施工期间对后续施工段落进行了锚杆支护参数优化，优化后各部位锚杆长度及环向间距见表9，纵向间距均为0.8 m。选取DK288+251断面对优化后各部位典型锚杆进行受力监测，结果如图11所示。

表9 优化后系统锚杆支护参数Table 9 Support parameters of systematic anchor bolt after optimization

图11 优化后DK288+251断面各部位典型锚杆实测轴力分布图 (单位：kN)Fig.11 Axial force distribution of systematic anchor bolt after optimization (unit:kN)

根据监测结果显示，初期支护内的其他测试数据，如喷射混凝土应变及钢架应力等数据均小于理论计算的数值；二次衬砌与初期支护的接触压力、二次衬砌混凝土及钢筋受力其数值极小。结果表明，采用优化后的锚杆参数，结构是安全稳定可靠的。

与施工图原设计(拱墙范围锚杆长5 m，间距0.8 m)相比，系统锚杆布置采用优化后的支护参数(见表9)，每延米隧道可节省锚杆约150 m，节省约41.4%，节省造价约4 900元。

4 结论与建议

1)结合乌蒙山2号4线车站隧道出口浅埋段实际工程，运用数值模拟与现场实测的方法，对4线大跨度浅埋隧道锚杆受力特征进行分析，结果表明：左、右侧对称部位锚杆轴力差值较小，即由于分部先后开挖引起对称部位锚杆轴力左右不对称的情况不明显；不同部位锚杆轴力差异较大，分布规律表现为边墙部位锚杆轴力>拱肩部位锚杆轴力>拱顶部位锚杆轴力。

2)结合乌蒙山2号4线大跨浅埋隧道锚杆受力特性，基于“按需配置，充分发挥锚杆支护能力”的原则，提出系统锚杆支护“部位不等参”设计理念，即对系统锚杆采取“不同部位不等参支护，左右对称部位等参支护”的布置方式，相比传统系统锚杆采用等长度、等间距的设计方式，既经济又能节省施工时间。

3)依托本工程，通过分别改变锚杆长度及间距进行系统锚杆不等参支护计算分析，并结合现场锚杆轴力监控量测验证，对较优的锚杆布置参数进行优化，优化后每延米隧道较施工图原设计(锚杆长5 m，间距0.8 m)节省造价约4 900元，经济效益显著。

建议下一步研究各级围岩不同埋深条件下按不同的开挖方法和顺序进行初期支护后前期环节支护与后续环节支护的关系，以提出大跨大断面隧道不等参支护的规律。