考虑盾壳与土体摩擦力的盾构下穿既有地铁隧道施工控制研究

来弘鹏，王腾腾，张林杰，袁 野，罗 维

(1.长安大学公路学院，陕西 西安 710064；2.中铁北京工程局集团有限公司，北京 102308)

0 引言

随着城市的发展，地下工程数量日益增多，新建隧道穿越已建隧道的工程也越来越多。盾构下穿施工过程中，不可避免对地层及既有隧道产生扰动，引起隧道结构的变形。因此，确保盾构施工时既有结构稳定、保障地铁正常运营已成为研究热点。

针对此，国内外众多学者从理论分析、数值模拟、模型试验等方面进行研究，取得了相应的成果。例如：Yin等[1]以深圳地铁9号线下穿4号线隧道为例，研究了EPB盾构盾尾空隙对既有建筑物沉降的影响，并利用三维有限元法分析了MJS工法的作用；Lin等[2]基于长沙地铁某工程，利用数值模拟研究了新建双线隧道斜下穿时既有隧道的变形、内力特性，分析了盾构隧道施工对地表沉降槽的影响；Li等[3]采用自动高性能全站仪系统连续监测了深圳地铁蛇口线双跨隧道在不同下穿阶段的位移以及衬砌性能；Jin等[4]基于深圳地铁下穿施工实例的大量监测数据，分析了新建盾构隧道下穿时既有隧道及地表的变形和衬砌应力，研究了既有隧道沉降的影响因素，并提出了一种预测既有隧道沉降的经验公式；张琼方等[5]以杭州地铁4号线近距离下穿既有地铁1号线为研究对象，对盾构施工参数、既有地铁变形进行监测，提出了保证既有隧道安全的施工措施；张冬梅等[6]基于Kerr 地基梁理论，建立了新建隧道施工对上方已建隧道影响的解析分析方法；魏纲等[7]基于 Mindlin 位移解和随机介质理论，考虑正面附加推力、盾壳与土体之间的摩擦力、附加注浆压力和土体损失，研究了类矩形盾构施工引起的土体竖向位移及各因素的影响；张治国等[8]基于镜像法与 Winker 地基模型，提出了类矩形盾构隧道施工诱发邻近管线变形的简化计算方法；来弘鹏等[9]以西安地铁1号线二期下穿既有1号线出入段线为依托，通过现场调研、数值模拟和现场监测等方法研究了施工参数对既有隧道轨道高差的沉降影响规律；林志军[10]以长沙地铁3号线盾构隧道下穿武广高速铁路浏阳河隧道工程为依托，采用理论分析、数值计算等方法对盾构下穿施工过程中既有高铁隧道响应规律进行了研究。

综上所述，关于盾构施工的数值模拟工作已取得较大进展。如文献[11-14]在模型中考虑了盾构土舱压力、注浆压力、浆液硬化的影响；文献[15]在计算中考虑了等代层与盾尾空隙的关系；文献[16]则提出了一种考虑地层损失率的动态调控方法。但目前关于盾构下穿的计算模型大多进行了简化，鲜有考虑盾壳与周围土体摩擦力的实际分布对计算结果的影响，而摩擦力又是盾构掘进引起既有隧道附加应力变化、水平及竖向位移的重要因素[17-19]；另外，在黄土地区盾构下穿过程中土舱压力、摩擦力、注浆压力等施工参数对既有隧道结构变形的影响尚不完善。

鉴于此，本文综合考虑盾构自重、盾构四周土压力实际分布特征，推导盾构掘进中盾壳与土体摩擦力计算公式，并采用FLAC 3D有限差分软件的Fish语言，模拟盾构下穿施工流程；依托西安地铁5号线新建盾构隧道近距离下穿已建2号线的工程实际，设计接近区、穿越区和脱离区3个区段施工参数调整方案；研究盾构下穿过程中既有隧道左右线竖向位移和横向水平位移规律、各施工参数对结构变形的影响机制，最终将模拟结果与现场实测数据对比，以验证研究成果的合理性。

1 工程概况

既有西安地铁2号线埋深9.4 m，为标准马蹄形断面，断面宽度6.3 m，高6.6 m，初期支护厚25 cm，二次衬砌厚30 cm；西安地铁5号线南稍门—文艺路盾构区间隧道左、右线将横向垂直下穿2号线南稍门站前区间隧道，下穿净距2.5～2.6 m，埋深18.5 m，其平面图和剖面图分别见图1和图2。

图1 西安地铁5号线下穿既有2号线平面图Fig.1 Plan view showing Xi′an metro line No.5 crossing underneath line No.2

图2 西安地铁5号线下穿既有2号线剖面图(单位:m)Fig.2 Profile showing Xi′an metro line No.5 crossing underneath line No.2 (unit:m)

2 盾壳与土体摩擦力计算公式及数值实现

2.1 盾壳与土体摩擦力计算公式

关于盾壳与土体摩擦力的计算，文献[18]通过将盾构两侧土压力简化为均布压力，给出了简化的计算模型，如图3(a)所示；考虑盾构两侧实际土压力的分布，本文对摩擦力计算公式进行了改进，如图3(b)所示。

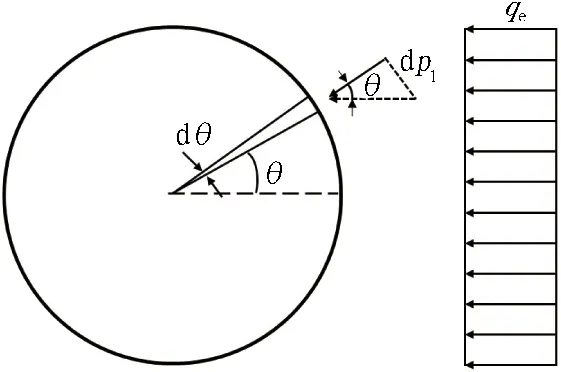
(a)简化计算模型

侧向土压力qe与竖向土压力pe1、pe2在盾构径向的分力p1、p2之和为支持力的大小，其中侧向土压力qe左右对称，计算公式为：

qe=Kγ[hN+r(1-sinθ)]。

(1)

式中：K为盾构所处地层的静止侧压力系数，一般按K=1-sinφ计算，φ为土体内摩擦角，(°);γ为土体容重，kN/m3；hN为盾构顶部埋深，m。

故侧向土压力在盾构径向单位长度的分力p1计算公式为：

dp1=[KγhNcosθ+Kγr(1-sinθ)cosθ]rdθ。

(2)

对于竖向土压力，考虑到盾构自重对底部土体的作用，其顶部土压力与底部土压力计算公式分别为：

pe1=γ[hN+r(1-sinθ)]；

(3)

(4)

式(3)—(4)中：W为盾构自重，kN;r为盾构刀盘半径，m；lsh为盾构长度，m。

故竖向土压力在盾构径向单位长度上、下部分的分力P2的计算公式分别为：

dp2上={γ(K+1)[hN+r(1-sinθ)]}rdθ；

(5)

(6)

因此，盾构与周围土体摩擦力的计算公式分别为：

dFf1=η(dp1+dp2上)dlsh；

(7)

dFf2=η(dp1+dp2下)dlsh。

(8)

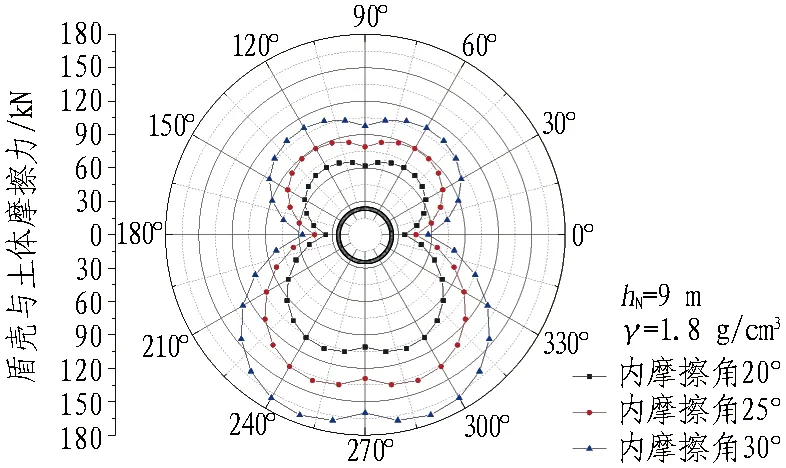
根据式(7)—(8)，盾壳与周围土体摩擦力分布形式如图4所示，表现为：1)盾壳与土体之间的摩擦力呈现上部小、下部大的特点(原因其一为盾构自重引起底部土体产生抗力，造成土体与盾壳之间接触压力的增大，进而引起摩擦力的增大；其二为深度不同造成盾构顶部与底部所受竖向、侧向土压力的差异)；2)摩擦力沿盾壳四周不均匀分布，且其分布形式与内摩擦角、盾构埋深、土体重度的改变无关，摩擦力最大位置为盾构下部与水平面约呈70°夹角处，摩擦力最小位置为盾构最左与最右侧；3)摩擦力大小与内摩擦角、隧道埋深、土体重度呈正相关性，但各因素对摩擦力的影响原因不同，内摩擦角的增大不仅造成摩擦系数的增长，同时也能导致静止侧压力系数的增大、水平土压力的增大进而引起土压力径向分力的增大，而埋深与重度的变化仅能造成土压力在径向分力的变化。

(a)

2.2 盾构施工参数计算及施工区段划分

根据文献[9-10]，目前常用的盾构土舱压力计算公式为：

pe=σh=K∑γh。

(9)

式中：pe为盾构土舱压力，kPa;γ为土体重度，kN/m3;σh为水平土压力；h为盾构隧道拱顶埋深。

注浆压力计算公式为：

(10)

根据式(9)—(10)，可求得本工程基准土舱压力为0.18 MPa，注浆压力为0.25 MPa。

盾构近距离下穿已建隧道时由于已建隧道部位土体被置换成隧道结构，其正面土压力值会发生显著变化[20]，因此，穿越中心水平土压力应为：

σh=K[γ(h1+h2)+T]。

(11)

式中：h1为既有隧道拱顶埋深，m;h2为既有隧道与新建隧道净距，m;T为既有隧道结构单位长度自重。

根据式(11)，本工程下穿中心土舱压力为0.14 MPa。考虑到注浆压力过大对既有隧道底部土体的扰动过大，结合工程实际取下穿段注浆压力为0.20 MPa。考虑到盾构施工每环土舱压力调整量不宜大于10 kPa，若每环调整过大，则易对既有隧道产生较大扰动，因此盾构施工参数由正常掘进参数调整到下穿参数时需要过渡区间。

结合文献[21]所述盾构隧道施工的影响范围，盾构下穿既有结构时次要影响范围

lI=(D+h2+2r)tanα。

(12)

式中：D为既有地铁隧道等效直径，m，可用等代圆法计算；α为盾构隧道影响角，(°)，取值范围一般为5°±φ/2。

根据式(12)，则本工程各区段长度分别为：

l1=l3=lI=13.37 m；

(13)

l2=2D+lS=21 m。

(14)

式(13)—(14)中：l1，l2，l3分别为接近区、穿越区和脱离区区段的长度；lS为既有隧道间距。

最终，本文选定既有隧道两侧一定范围为调整区间，设计了盾构下穿的工况设计方案，如表1及图5所示。

表1 盾构下穿施工参数设计方案Table 1 Construction parameters for shield tunneling MPa

图5 盾构下穿既有隧道分区示意图Fig.5 Segmentation of shield tunnel crossing underneath existing tunnel

2.3 数值实现

2.3.1 模型概况

根据隧道结构实际尺寸及圣维南原理，沿新建隧道轴线取70 m，沿既有地铁方向取70 m，上部地层取至地表，既有区间隧道结构与新建隧道间距2.5 m，如图6所示，模型最终大小为70 m×70 m×60 m。最终，模型共包括节点152 606个，单元307 402个。土层及隧道衬砌结构材料物理力学参数分别如表2和表3所示。土体采用摩尔-库仑模型，既有隧道衬砌结构及新建盾构管片单元均采用弹性体模型；对模型底部及四周施加约束，上表面为自由面。注浆体等代层物理参数依据文献[11]和[22]并结合盾构掘进试验段浆液抗压强度现场测试结果拟定。

图6 计算模型Fig.6 Calculation model

2.3.2 盾构下穿施工过程模拟

新建5号线盾构隧道采用刚度迁移法进行模拟(见图7)，每次循环开挖一个管片长度(1.5 m)；考虑盾构的长度及质量，对盾壳单元采用弹性体模型，根据工程实际赋予相应的重度、弹性模量等参数，土舱压力通过对掌子面施加面荷载模拟，注浆压力通过对土体施加径向荷载模拟，摩擦力通过对盾壳外围土体施加对应大小的横向荷载模拟，顶推力通过对管片单元施加节点力模拟。根据计算公式，摩擦力并不是均匀分布在盾壳与土体接触面上的，每一点处的摩擦力大小均与该点对应的坐标和角度有关，因此本文通过FLAC 3D内置的Fish语言，以角度和坐标为变量，在与盾壳接触的土体部分施加对应大小的荷载的方法，模拟摩擦力对土体的影响，以提升数值计算结果的准确性，使其结果更加贴合实际工程。

表2 土层物理力学参数Table 2 Physico-mechanical parameters of soil

表3 材料物理力学参数Table 3 Physico-mechanical parameters of material

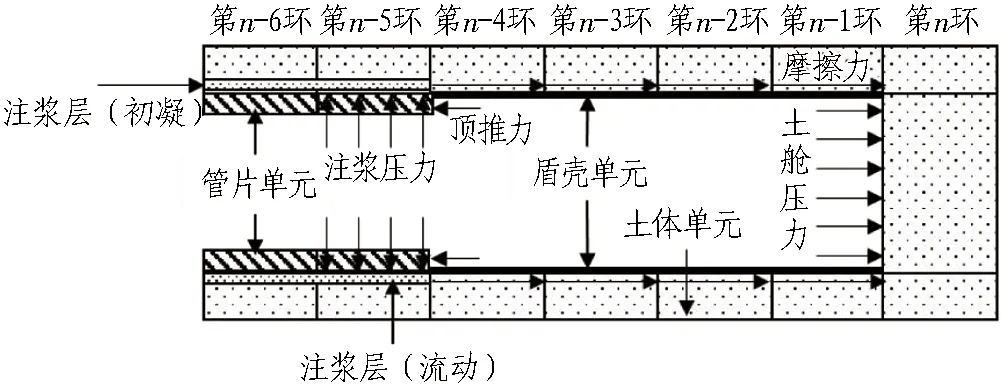
n代表盾构掘进时的环数。图7 新建盾构隧道施工过程模拟Fig.7 Simulation of construction process of shield tunnel

2.3.3 监测点布置

由于既有隧道受盾构施工扰动最大的位置一般位于其与新建隧道轴向交叉处，故在新建隧道轴向上方的既有隧道断面处设置拱顶、仰拱、拱腰4个监测点，如图8所示。

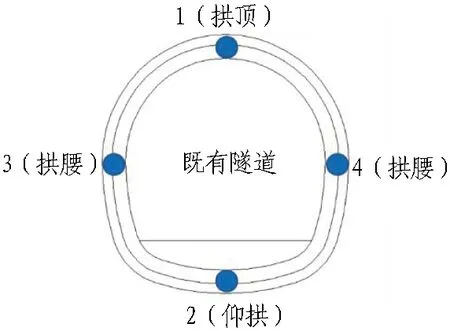
图8 既有隧道监测点设置图Fig.8 Layout of monitoring points for existing tunnel

3 计算结果分析

3.1 盾构逐环掘进中既有隧道结构位移规律

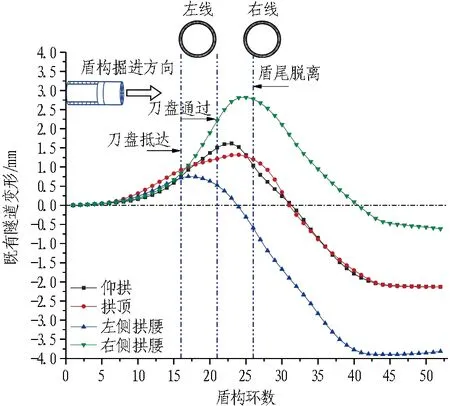
图9示出各工况既有隧道结构拱顶、仰拱、拱腰随盾构逐环推进的位移曲线，由图可知：1)既有隧道拱顶、拱腰、仰拱处的竖向位移趋势均表现为先隆起、后沉降，各位置在盾尾脱离前一直保持隆起趋势，且随着刀盘接近，结构隆起逐步增大；而在盾构通过、压力消散后，各处变形曲线下降，隆起变形量均逐渐减小，表现为沉降趋势。既有隧道结构隆起的原因是盾构掘进对前方土体的挤压作用，土舱压力的施加使得前方土体产生附加接触压力[23-24]，摩擦力引起盾构四周土体产生与隧道掘进方向一致的水平位移，二者均引起前方地层的隆起，并进而造成既有结构随土体产生隆起位移。2)对比分析既有隧道结构竖向变形可知，各位置隆起量、横向水平位移量从大到小依次为右侧拱腰>仰拱>拱顶>左侧拱腰，右侧和左侧拱腰最大隆起量差分别为2.22、2.01 mm，横向水平位移差分别为1.98、1.70 mm。而位移曲线增长的区间与其受土舱压力、摩擦力、注浆压力综合作用的时间一致，各因素对右侧拱腰作用时间最长，拱顶与仰拱次之，左侧拱腰最短，故结构各处隆起量大小及隆起趋势持续时间主要取决于其受盾构掘进过程中土舱压力、注浆压力、摩擦力作用的时长。3)由于盾构掘进先下穿通过既有隧道左线后下穿右线，土舱压力、注浆压力、摩擦力对左右线既有隧道作用的时间不同，造成变形曲线中二者量值、增减趋势的差异；在竖向位移方面，右线既有隧道结构与左线拱顶、仰拱、左侧拱腰、右侧拱腰最大隆起量差分别约为1.96、1.98、1.82、2.01 mm；横向水平位移方面，左右线既有结构横向位移均表现为随刀盘接近而增大，盾尾通过后逐渐稳定的趋势，二者最大变形量差较小，拱顶、仰拱、左侧拱腰、右侧拱腰4个监测点分别为0.19、0.46、0.33、0.30 mm，但隧道左右线结构变形稳定所需的时间不同，左线水平变形约在盾构掘进至35环时稳定，右线则需在掘进至45环时才趋于稳定。

(a)既有隧道左线竖向位移

3.2 既有结构位移影响因素研究

选取土舱压力pe=0.09～0.18 MPa、注浆压力pg=0.10～0.25 MPa、摩擦因数ηf=0.20～0.50，对比不同工况下既有左线隧道右拱腰竖向位移进行影响分析。不同土舱压力条件下既有结构位移曲线见图10，由图可知，随着土舱压力的增大，既有结构在刀盘到达前(0—21环)的隆起趋势增强，在盾构通过时(16—26环)的隆起值增大，盾尾脱离至施工完成阶段(26—52环)的沉降值减小。各工况竖向变形曲线之差在盾构下穿段逐渐增大，在盾尾脱离处达到最大，结合图11和12中盾尾脱离前(0—26环)各曲线相差极小，表明此过程既有结构竖向位移受土舱压力影响程度最深；而在盾构离开后不同工况既有结构竖向位移差值变动较小，施工完成后其沉降大小差异的原因为先前隆起量的不同，表明盾构脱离后既有结构竖向位移受土舱压力影响程度较小，故土舱压力的主要作用区间为盾尾脱离前(0—26环)。

图10 不同土舱压力条件下既有结构位移曲线Fig.10 Displacement of existing structure under different soil chamber pressures

不同注浆压力条件下既有结构位移曲线见图11，由图可知，注浆压力的变动对盾尾脱离前既有结构竖向位移变化并无明显作用，其对既有结构位移的主要影响区段应为盾尾脱离至施工完成阶段(26—52环)，且表现为随着注浆压力的增大，作用在盾尾空隙上的支护压力增大，既有结构在盾构通过后的沉降量减小，沉降趋势放缓。因此，为减小盾构通过后地层及既有结构的沉降，应及时进行盾尾注浆，并设置合理的注浆压力。

不同摩擦因数下既有结构变形曲线见图12，由图可知，摩擦力对既有结构位移的影响区段可分为盾构机身通过阶段(21—26环)与盾尾脱离后阶段(26—52环)。在盾构机身通过阶段，结构隆起量随着摩擦力的增大而增加，而盾尾脱离后随着摩擦力的增大，既有结构竖向沉降值及沉降趋势逐渐增大。其原因应为盾构机身通过时摩擦力带动周围土体产生与掘进方向一致的水平位移，土体向前位移引起前方地层隆起，使既有结构随之向上隆起；而盾构通过后摩擦力又造成盾尾后方空隙增大，上方地层向下移动填补空隙，造成了地层沉降的加剧，并使得既有隧道随之产生沉降，因此，过大的摩擦力对地层及既有结构的稳定有较大负面影响，工程中应及时向盾壳周围注入膨润土泥浆，以尽量减少盾构掘进时盾壳与土体之间的摩擦力。

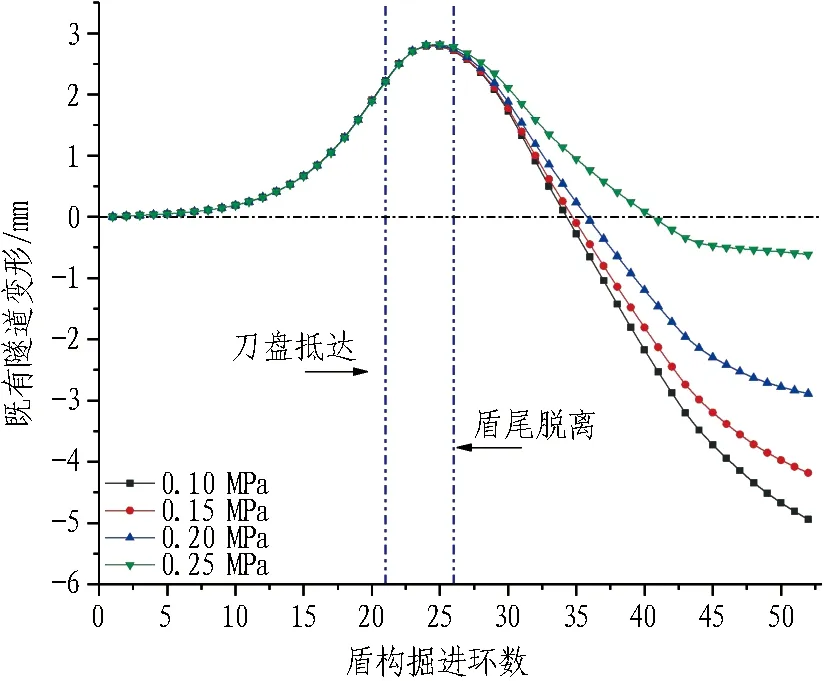
图11 不同注浆压力条件下既有结构位移曲线Fig.11 Displacement of existing structure under different grouting pressures

图12 不同摩擦因数下既有结构变形曲线Fig.12 Displacement of existing structure under different friction coefficients

4 现场实施效果评价

4.1 现场监测点布设

为评价2.2节计算给出的盾构下穿施工参数、参数调整区间对已建2号线区间隧道变形的控制效果，并验证数值计算结果的准确性，在盾构施工影响范围(DK15+389～+449)内设置11个监测断面，如图13所示；在每个监测断面内左右线隧道轨道道床及拱顶设置A—F6个监测点，如图14所示，对既有区间隧道变形进行监测。

图13 监测断面布设图Fig.13 Layout of monitoring section

图14 现场监测点布设图Fig.14 Layout of monitoring points

4.2 现场监测结果分析

双线盾构隧道施工完成后，实测既有区间隧道左右线道床变形及数值模拟计算结果如图15所示。本文采用考虑摩擦力的计算模型，其结果与实测值误差为11%，较以往不考虑摩擦力计算模型小24%，且小于均匀分布模型的15%，表明了该模拟方法的正确性。实测值与计算曲线均表现为：道床最大变形处位于左线盾构隧道与其交叉位置测点；右线道床最大沉降处位于右线盾构隧道与既有隧道交叉位置测点处，对于盾构下穿工程而言，由于盾构施工中土体及土中隧道结构与盾构的距离最近，受施工参数影响最大，且施工后受施工影响原先被挤压的土体在盾构通过后孔隙水压的降低、释放会发生沉降，所以受盾构扰动最大的部分应当为新建隧道与既有隧道交叉位置，实际施工中应当对此区域多加监测；另外，既有隧道左右线道床变形虽略有不同，但最大沉降均小于6 mm，最大上浮小于5 mm，满足GB 50911—2013《城市轨道交通工程监测技术规范》[21]、CJJ/T 202—2013《城市轨道交通结构安全保护技术规范》[25]中的要求，因此本文确定的施工参数对于控制道床变形起到良好效果。

(a)既有隧道左线道床A测点变形

图16示出既有2号线区间隧道衬砌拱顶沉降变化及实测与计算对比。实测值与本模型计算结果偏差较小，误差约14%，远小于不考虑摩擦力计算模型的31%，且小于均匀分布模型的23%。与道床沉降类似，隧道拱顶变形曲线较为符合“沉降槽曲线”[26-27]的形式，最大沉降处位于盾构隧道中心线上方，距离盾构轴线越远沉降量越小；右线隧道拱顶沉降整体较小，最大沉降仅为1.91 mm，证明了施工盾构参数调整较为及时有效；在采用本文所提出的施工参数调整后，既有隧道左右线最大拱顶沉降量均小于6 mm，符合GB 50911—2013《城市轨道交通工程监测技术规范》[21]、CJJ/T 202—2013《城市轨道交通结构安全保护技术规范》[25]中的要求，因此本文确定的施工参数对于拱顶沉降的控制效果也较为理想。

(a)既有隧道左线E测点变形

5 结论与建议

1)考虑盾壳自重及盾构四周土压力的分布特征，推导了盾壳-土体摩擦力的计算公式，分析了其分布特征，并基于Fish语言应用于FLAC 3D中，较为真实地反映了盾构下穿过程中盾壳与土体之间摩擦力对既有结构的影响。

2)在下穿过程中，既有隧道结构竖向变形表现为随盾构逐环推进结构逐渐隆起，在盾构离开、压力消散后呈现沉降的趋势；横向水平位移则表现为随盾构接近而逐渐增大，盾尾通过后逐渐稳定；由于土舱压力、摩擦力、注浆压力扰动程度不同，左右线隧道结构之间、隧道不同结构之间变形差异较大，两隧道结构变形量由大至小依次为右侧拱腰>仰拱>拱顶>左侧拱腰；既有结构隆起为右线大于左线。

3)在盾构下穿的不同阶段，既有结构竖向位移的主要影响因素不同。在刀盘到达前，既有结构的隆起主要受土舱压力影响；而在盾构机身通过时，既有结构的竖向隆起随土舱压力、摩擦力的增大而增大；在盾尾通过后，既有结构的沉降随注浆压力的增大以及摩擦力的减小而减小。因此，应设置合理的施工参数，并及时注入膨润土泥浆等措施减小摩擦力，以稳定开挖面、减少地层及既有结构的沉降。

4)根据现场实测数据反馈，本模型计算结果与实测值偏差分别约为10%和14%，小于不考虑摩擦力和均匀分布摩擦力的计算模型，验证了本文对摩擦力影响分析的合理性及数值模拟方法的准确性；既有运营中2号线隧道道床最大变形量及拱顶最大沉降量均小于规范所要求的6 mm，表明本文所确定的盾构施工参数及参数调整方法对于控制本工程既有隧道变形、保障运营安全起到了良好的控制作用。

5)由于本文在计算过程中未考虑地下水、运营列车荷载、地面建筑物的影响，造成计算结果与实测值仍有一定偏差，因此，建议在之后的研究中可针对以上因素进行更加全面细致的分析。