基于子集模拟的建设工程项目多资源均衡优化算法

王家，刘可心，张学清，陈涛

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.湖南大学建筑安全与环境国际联合研究中心，湖南长沙 410082；3.香港科技大学 土木与环境工程系，香港 999077；4.长沙市美的房地产开发有限公司，湖南 长沙 410082）

建设项目的施工过程需消耗大量的人工、材料、机械等资源.如果建设项目实施过程中的资源计划（劳动力计划、材料进场计划、机械排班等）安排不合理，会引起建设项目工期内资源消耗量的过大波动（表现为施工人员的窝工或少工、材料和机械的过度使用或空置等），最终影响建设工程的生产效率、成本节约和项目管理质量[1].作为资源调度优化的手段之一，资源均衡问题（Resource Leveling Problem，RLP）旨在通过调整项目中非关键工序的计划开始时间，在不延长项目工期和不违反各工序间逻辑关系的前提下，降低项目工期内资源消耗量的波动.

针对资源均衡问题的研究工作可分为两类，一类偏重于资源均衡问题的模型构建，一类偏重于资源均衡问题的优化算法.资源均衡优化模型一般可归结为四类：简单的平方和模型[2-3]、考虑实际资源消耗量与期望值之间差值的偏差模型[1，4-5]、考虑不同周期资源消耗量变动的波动模型[6-7]、以及基于熵理论的熵模型[8-9].资源均衡问题的优化算法主要分为精确算法和启发式算法.其中，精确算法主要基于动态规划、整数规划、分支定界法等方法[10]，而启发式算法主要基于蚁群算法[11]、粒子群算法[12]、禁忌搜索算法[13]、遗传算法[14-18]等算法.资源均衡问题的复杂程度随涉及工序数量的增加而急速上升.因此，针对工序数量较多的项目资源均衡问题，精确算法并不适用，只能采用启发式算法.但是，启发式算法具有随机性，其每次运行获得的最优解不一定相同（不稳定），但现有启发式算法在最优解获取稳定性上仍有较大的改进空间.

本文针对建设工程项目的多资源均衡优化问题，提出一种基于子集模拟的启发式优化算法.同时，为避免工序间逻辑关系违反时复杂修复算子的使用，本文采用间隔率变量表示的建设工程项目多资源均衡优化模型，以简化基于子集模拟的优化算法的操作.通过算例验证，与应用较广的遗传算法相比，本文提出的优化算法在最优解获取稳定性上有较好的改进.

1 建设工程项目多资源均衡优化模型

针对建设工程项目的多资源均衡优化问题，研究者一般借助网络计划工具进行分析，并在一定的假设下构建模型.本文研究的多资源均衡优化模型基于以下假设：

1）组成建设项目的各个工序必须连续施工，不能间断，且各工序间的逻辑关系不随时间改变.

2）组成建设项目的各个工序在实施期内，单位时间内耗费资源的种类和数量保持不变.

3）建设项目的总工期保持不变.

考虑一个包括N 个工序、且实施过程中涉及K种资源的建设工程项目.设项目中每一个工序i 的持续时间为Di，i=1，…，N，其持续时间内每单位时间消耗的第k 种资源为，k=1，…，K.根据各工序的持续时间和相互间的逻辑关系，可采用关键路径法（Critical Path Method，CPM）计算出各工序的最早开始时间ESi和最晚开始时间LSi，i=1，…，N，以及项目的总工期T.

建设工程项目多资源均衡优化的目标是通过合理安排各工序的计划开始时间Si，i=1，…，N，使项目实施期内资源消耗的波动最小.考虑到各工序间的逻辑关系和项目总工期T 保持不变的要求，各工序的计划开始时间Si，i=1，…，N 需满足下述限制：

式中：pred（i）代表工序i 的所有紧前工序的集合.

在给定各工序的计划开始时间S=[S1，S2，…，SN]下，项目在总工期T 内任意时刻t 所消耗第k 种资源的数量（S），t=1，…，T，k=1，…，K，可由该时刻正在施工的所有工序所消耗第k 种资源的数量汇总得到，即：

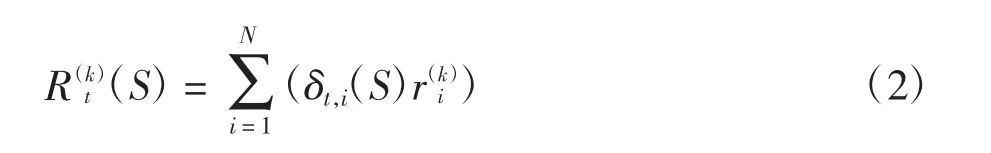
式中：δt，i（S）为t 时刻工序i 是否正在实施的指示变量，δt，i（S）=1 如Si≤t ≤Si+Di（t 时刻工序i 正在实施，如图1 所示），否则δt，i（S）=0，，k=1，…，K 为工序i 单位时间内第k 种资源的消耗量.

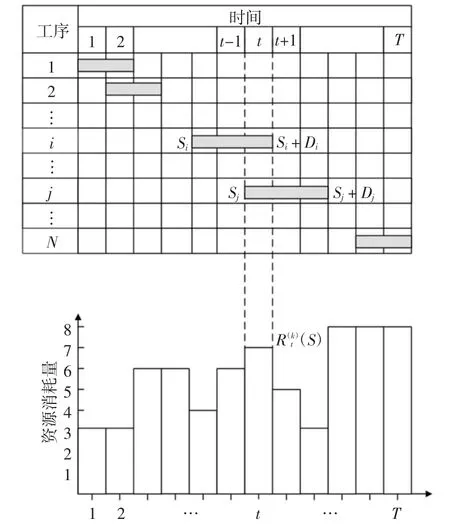
图1 资源消耗量Fig.1 Resource consumption

在得到项目总工期内施工所需各资源在不同时刻的消耗量后，可计算出用于衡量项目资源均衡效果的指标.针对资源均衡问题，研究者从不同角度出发，提出了反映资源消耗量不均衡程度的多种指标，但学术界尚未在各指标的优劣上达成共识.从统计学角度看，标准偏差指标可较好地反映项目在不同时刻资源消耗量的不均衡程度，在资源均衡优化问题中采用较广[12，16，19].因此，本文采用标准偏差指标来构造建设工程项目多资源均衡优化模型，但文中所提出的多资源均衡优化算法与所选指标无关，亦适用于其他指标的情形.基于项目在总工期内任意时刻t 所消耗第k 种资源的数量（S），t=1，…，T，k=1，…，K，总工期内第k 种资源消耗量的标准偏差 为σ（k）（S）：

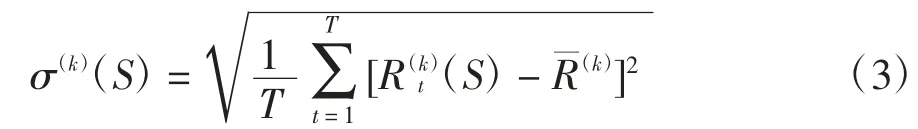
在项目多资源均衡优化问题中，为消除不同资源消耗量数量级、单位等的影响，本文将标准偏差无量纲化，采用标准偏差与平均消耗量的比值σ（k）（S）/来代表每一种资源的均衡效果.同时，为反映不同资源在多资源均衡优化问题中的重要性，可针对不同资源分配不同的权重系数，将目标函数定义为不同资源无量化标准偏差的线性加权：

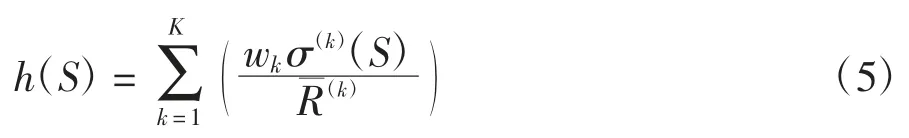
式中：wk为第k 种资源的相对权重，满足=1，可采用层次分析法和德尔菲法、专家模糊综合评分法、基于专家权重聚类的权重优选法等方法确定[19].

综上所述，本文研究的建设工程项目多资源均衡优化模型可定义为：

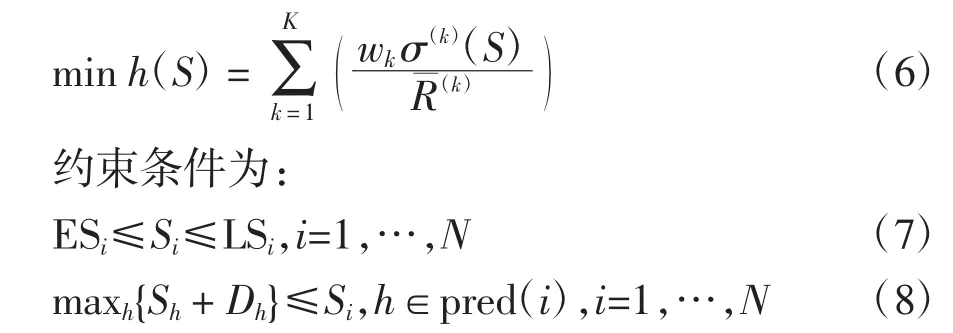
2 采用间隔率变量表示的建设工程项目多资源均衡优化模型

针对资源均衡问题的优化算法中，各工序计划开始时间（优化问题的设计变量）通常直接在其最早开始时间和最晚开始时间之间取值，即ESi≤Si≤LSi，i=1，…，N.但是，这种设计变量的取值方式，容易违反工序间的逻辑关系（不满足公式（8）对应的约束条件），需要引入复杂的修复算子来调整设计变量的取值.考虑图2 所示的简单建设工程项目的单代号网络图，图中标明了各工序的持续时间、最早开始时间、及最晚开始时间.由图2 可知，该网络中的非关键工序为工序2 和工序4.如直接在工序最早开始时间和最晚开始时间之间取值，工序2 和工序4 的计划开始时间可以分别取7 和8，但这样的取值显然违反工序2 与工序4 的逻辑关系.具体而言，因工序2为工序4 的紧前工序，在工序2 的计划开始时间为7的条件下，工序4 的最早开始时间变更为9，其计划开始时间不能取8.

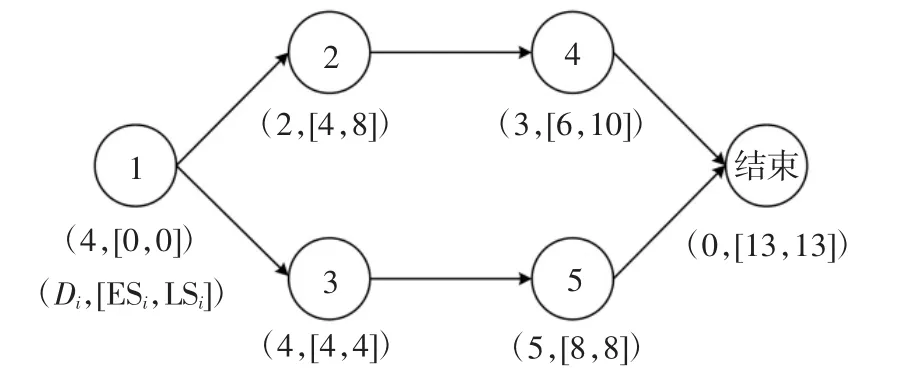
图2 典型建设工程项目的单代号网络图Fig.2 Activity-on-node network of a typical construction project

为避免上述取值方式的问题，本文采用文献[16]中提出的工序计划开始时间的间隔率表示方法.具体而言，考虑到LSi≤maxh{Sh+Dh}，h∈pred（i），可将公式（7）和（8）对应的约束条件合并，即工序i 的计划开始时间Si取值范围为：

如将区间[0，1]等分为（LSi-max{Sh+Dh}+1）个子区间，则这些子区间与Si可取的（LSi-max{Sh+Dh}+1）个整数间存在一一对应的关系.因此，可定义在区间[0，1]连续取值的变量xi（间隔率变量），并根据其所在子区间，映射到工序i 的计划开始时间Si，

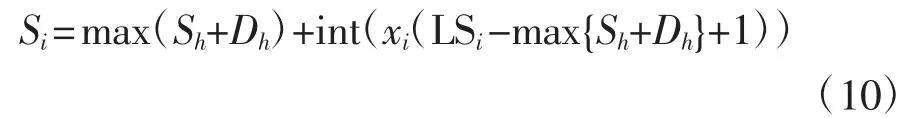
式中：int（）为取整函数.针对图2 所示的简单项目，如工序2 和工序4 的间隔率变量分别取0.73 和0.14，利用公式（10）可求得相应的计划开始时间分别为4+int（0.73×（8-4+1））=7 和9+int（0.14×（10-9+1））=9.显然可见，通过工序计划开始时间的间隔率变量表示，可避免违背工序间的逻辑关系.

利用间隔率变量和计划开始时间之间的映射（公式（10）），原始的离散变量优化问题（公式（6）～（8））可转化为如下的连续变量优化问题：

约束条件为：

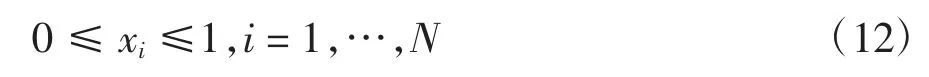
式中：g（x）为间隔率变量x=[x1，x1，…，xN]对应的目标函数.为计算目标函数值g（x），可首先利用公式（10）计算给定x 对应的各工序的计划开始时间S=[S1，S2，…，SN]，进而代入原始优化问题的目标函数h（S）（公式（6））.

3 基于子集模拟的多资源均衡优化算法

子集模拟法（Subset Simulation）是Au 和Beck 提出的、针对结构可靠度问题的高效数值模拟算法[20].其思想是通过引入一系列中间失效事件，将偶发事件的小概率估计问题转化为一组较大的条件概率估计问题，进而提高数值模拟算法的计算效率.通过建立可靠度问题和优化问题的内在联系，子集模拟法也在优化设计问题中取得了较好的应用[21-22].

3.1 基于子集模拟的多资源均衡优化框架

考虑如下的全局优化问题：

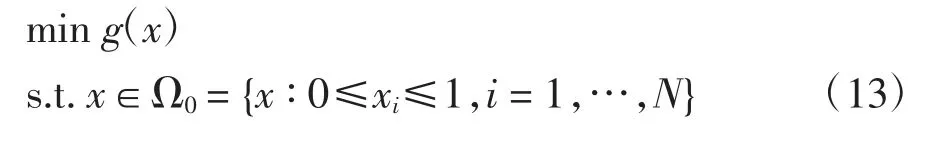
为利用子集模拟法求解上述优化问题，人为设定设计变量x 为随机变量，服从可行域Ω0={x ∶0≤xi≤1，i=1，…，N}内的均匀分布.此外，子集模拟法通过引入一系列递减的边界值g1＞g2＞…＞gJ，在可行域Ω0内定义一系列逐渐收缩的区域Ωj={x ∶x∈Ω0，g（x）≤gj}，j=1，…，J.其中，每一区域为之前区域的子集，即Ω0⊇Ω1⊇Ω2…⊇ΩJ.通过依次在可行域Ω0及逐渐收缩区域Ωj（j=1，…，J）内按均匀分布进行随机取样，子集模拟法可逐渐缩窄搜索区域，最终在最优解附近的较小区域进行搜索，以得到问题的最优解.

基于子集模拟的优化算法有两个重要参数：在指定区域中抽样的样本数量M 及条件概率参数p0.参数M 和p0的选择，需确保Mp0和1/p0均为正整数.由于Mp0确定了每一迭代中收缩区域初始样本点的数量，当p0过小时，需要较大的样本数量M 才能保证Mp0的数值不至过小，以达到对收缩区域的有效搜索.当p0过大时，迭代中考察区域的收缩变慢，优化算法需要较多的迭代次数.综合目前的研究成果，p0一般在0.05～0.3 区间取值，进而根据可承受计算资源确定样本数量M.在参数确定后，基于子集模拟的优化算法首先在可行域Ω0内，产生服从均匀分布的M 个设计变量样本，并计算它们的目标函数值.接着，将目标函数值由小到大排序，并取排在第Mp0位置的目标函数值作为定义区域Ω1={x ∶x∈Ω0，g（x）≤g1}的边界值g.此时，之前产生的M 个设计变量样本（服从可行域Ω0内的均匀分布）中，有Mp0个落在定义的收缩区域Ω1内（服从收缩区域Ω1内的均匀分布）.因此，可采用马尔科夫链蒙特卡罗模拟方法（Markov chain Monte Carlo simulation，MCMCS，详见3.2 节），以这Mp0个设计变量样本作为Mp0个链条的起点，并针对每一链条额外产生（1/p0-1）个状态点，以产生区域Ω1内服从均匀分布的M 个设计变量样本

图3～图6 描述了参数M=20 和p0=0.2 时的上述流程.针对图3 可行域Ω0内服从均匀分布的20个设计变量样本，图4 给出了它们所对应的目标函数值的升序排列.此时，定义下一收缩区域Ω1的边界值g1，由20 个目标函数值中第Mp0=4 小的数值确定，见图4.对应上述确定的g1，之前可行域Ω0内均匀分布的M=20 个设计变量样本，有Mp0=4 个落在收缩区域Ω1={x ∶x∈Ω0，g（x）≤g1}内，见图5.为产生收缩区域Ω1内均匀分布的M=20 个设计变量样本，可采用MCMCS 方法，以目前的Mp0=4 个样本为种子，分别产生4 条马尔科夫链链条，见图6.每条链条以其中一个种子为起点，额外产生（1/p0-1）=4 个状态点，以确保总的样本数为Mp0（1/p0-1+1）=M=20.

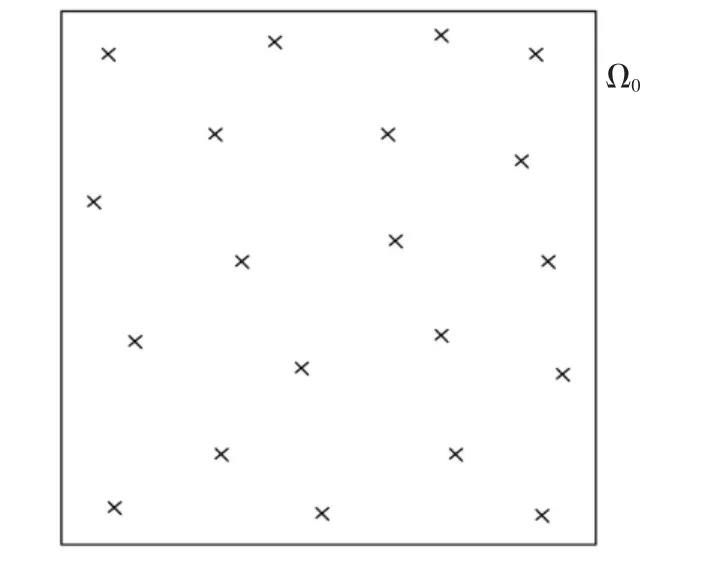
图3 可行域Ω0 内均匀分布的设计变量样本点（M=20）Fig.3 Samples of the vector of design variables uniformly distributed in the feasible region Ω0（M=20）

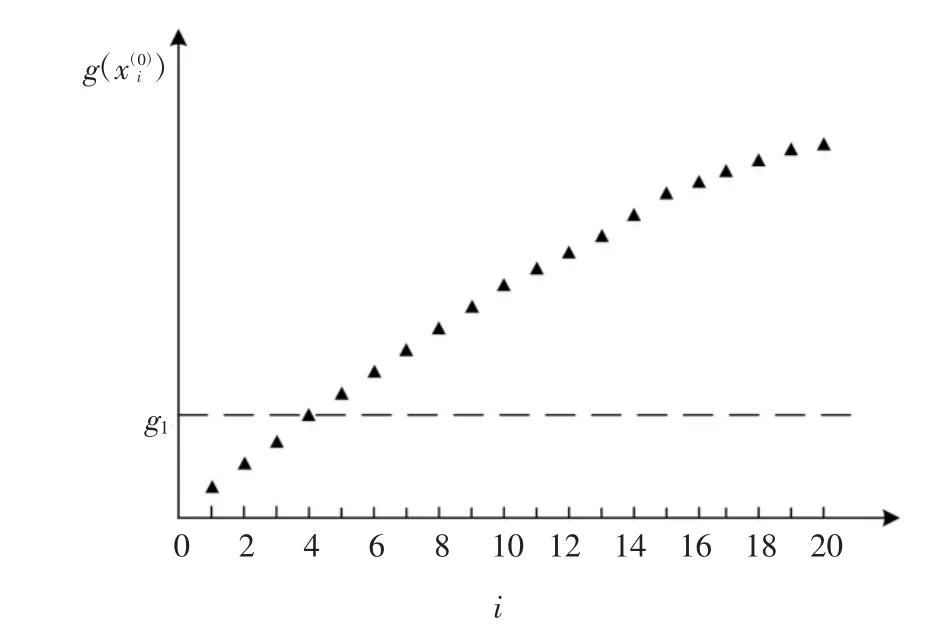
图4 定义收缩区域Ω1 的边界值g1（M=20，p0=0.2）Fig.4 Threshold value of g1 for the shrinking region of Ω1（M=20，p0=0.2）

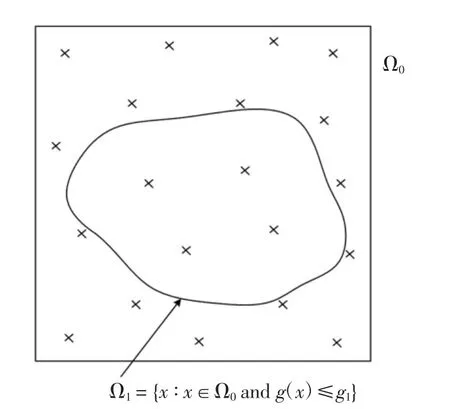
图5 收缩区域Ω1 及落入其中的初始样本点（M=20，p0=0.2）Fig.5 Shrinking region of Ω1 and the seed samples in Ω1（M=20，p0=0.2）

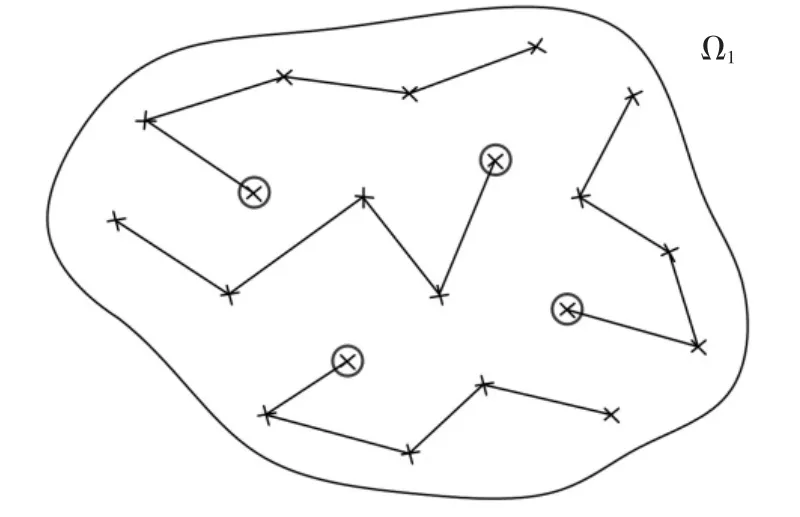
图6 区域Ω1 内均匀分布的设计变量样本点Fig.6 Samples uniformly distributed in Ω1

得到区域Ω1内服从均匀分布的M 个设计变量样本后，可依次迭代重复上述边界值的确定和对应收缩区域内随机样本点的产生流程，直到优化算法的迭代终止原则满足为止.此时，选择最终的收缩区域中随机样本点的最优者作为问题的最优解.

3.2 收缩区域Ωj={x ∶x∈Ω0，g（x）≤gj}内均匀分布样本点的产生

如3.1 节所述，基于子集模拟的多资源均衡优化算法中，需根据收缩区域Ωj内均匀分布的少量样本点，利用MCMCS 方法产生满足要求数量的样本点.考虑到多资源均衡优化问题中设计变量的维数（对应项目涉及的工序数量）可能较大，本文采用改进Metropolis-Hasting 方法[20]完成马尔科夫链的产生任务.

采用p*（ξ/x）来表示以x 为中心点，以d 为宽度（即x-d/2 ≤ξ ≤x+d/2）的一维均匀分布的概率密度分布函数，d 一般可取0.2～0.4.该概率密度分布函数自动满足对称性，即p*（ξ/x）=p*（x/ξ）.为产生给定样本点x1为起点的马尔科夫链{x1，x2，…}，本文利用改进Metropolis-Hasting 方法的思想，采用如下xk=[xk（1），xk（2），…，xk（N）]到xk+1=[xk+1（1），xk+1（2），…，xk+1（N）]的迭代操作：

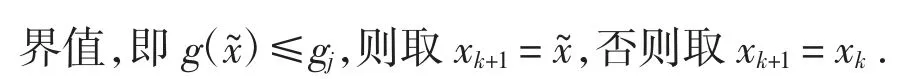
3.3 基于子集模拟的多资源均衡优化算法总结

针对采用间隔率变量表示的建设工程项目多资源均衡优化模型（公式（11）～（12）），本文基于子集模拟法，建议的优化算法步骤总结如下：

1）确定子集模拟算法中采用的参数，即在指定区域中抽样的样本数量M、条件概率参数p0和改进Metropolis-Hasting 方法中定义一维均匀概率分布的宽度d.

4）算法采用的迭代终止原则为达到预先设定的迭代次数J.如不满足迭代终止条件，即j ＜J，令j=j+1，重复步骤3.

4 算例分析

本文采用30 个工序组成的建设工程项目算例，来检验基于子集模拟的多资源均衡优化算法的性能.基于标准算例库PSPLIB（Project Scheduling Problem Library）[23]中算例j301_1 的数据，表1 给出了算例项目的具体信息，包括项目中各工序的紧前工序（第3 列）、各工序的持续时间（第4 列），各工序每天对应需求的4 种资源（人工、水泥、碎石、自卸车）的消耗量（第5～8 列）.根据各工序的持续时间和工序间的逻辑关系，可计算出该建设工程项目的工期为T=38 d.因标准算例库在模型构建方面的信息并不充分，没有提供项目管理专家所需的针对权重指标判断的有效信息.因此，各资源的相对权重选择确定为[w1，w2，w3，w4]=[0.2，0.2，0.4，0.2]，如项目的信息足够，需采用专家判断法确定.

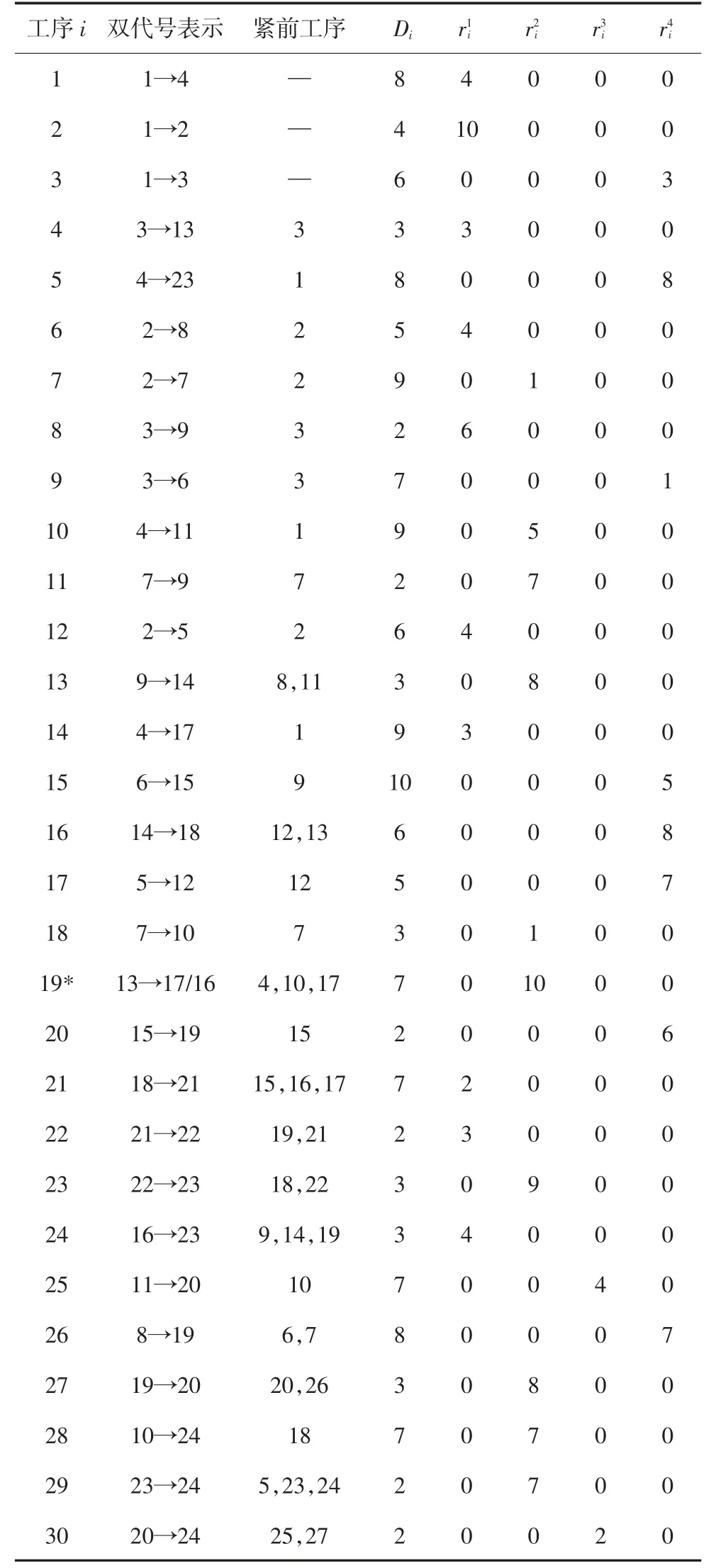
表1 算例数据Tab.1 Data of the example

为检验基于子集模拟的多资源均衡优化算法的性能，每代随机抽样样本数量取M=2 000，条件概率参数取p0=0.1，改进Metropolis-Hasting 方法中一维均匀概率分布的宽度取d=0.3.图7 描述了基于子集模拟的建议优化算法一次典型求解过程中，最优目标函数值随迭代阶段的变化.由图7 可知，算法经过19 代迭代后收敛到最优解，对应最优目标函数值1.115 4.该最优解对应的各工序计划开工时间Si如表2 所示.为直观对比优化前后各工序的开工时间，图8 和图9 绘制了优化前后的双代号时标网络图，各工序在图中的双代号表示见表1 第2 列.

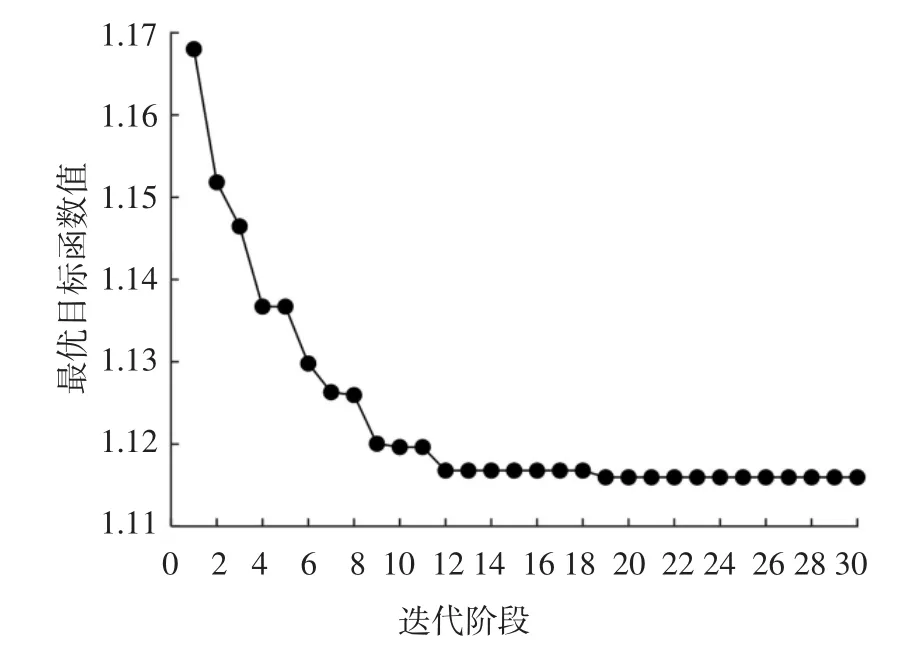
图7 最优目标函数值随迭代阶段的变化Fig.7 Optimal objective function value at different stages

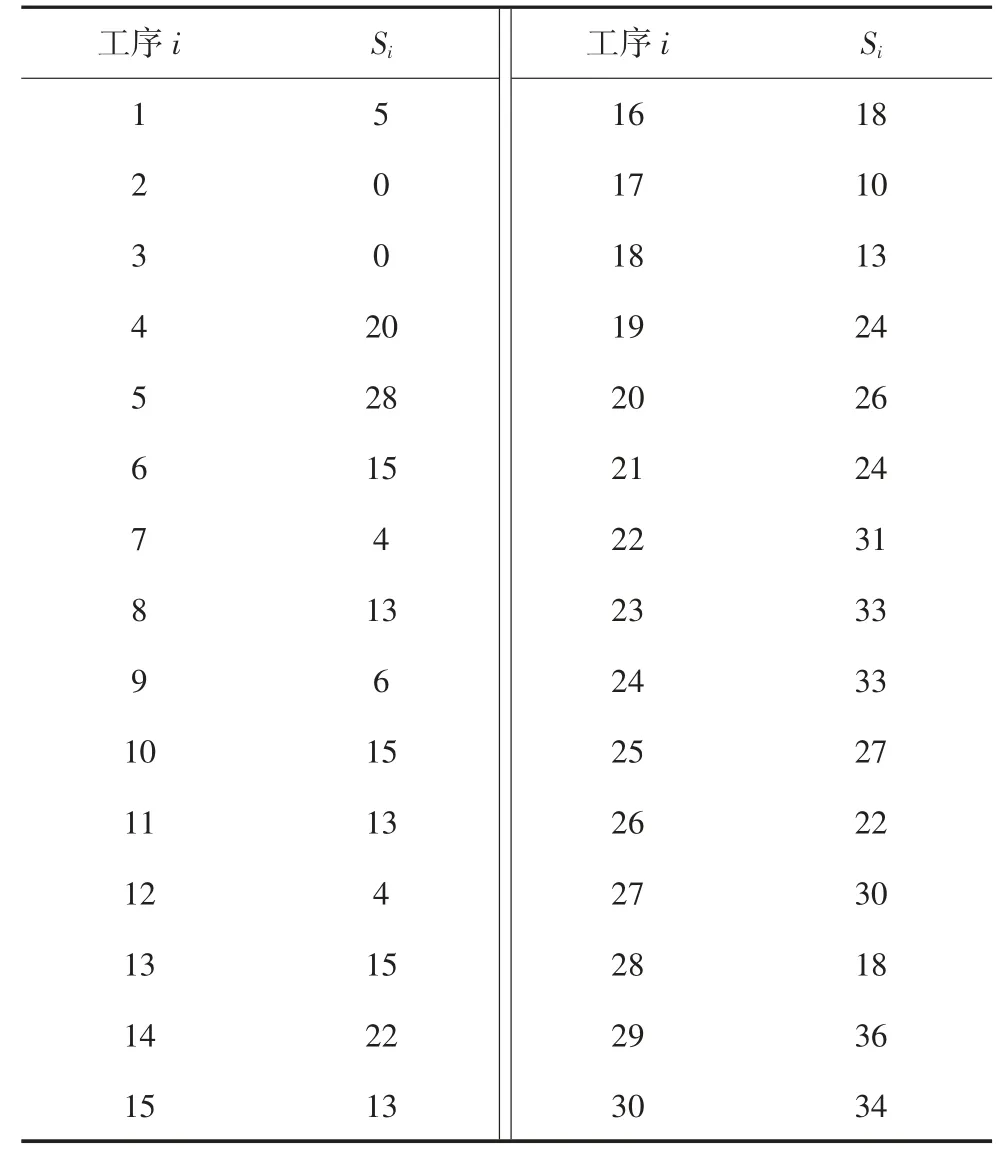
表2 典型最优解对应的工序计划开工时间Tab.2 Scheduling time for the activities corresponding to the optimal solution

图8 优化前算例的双代号时标网络图Fig.8 The activity-on-arc time scaled network before optimization

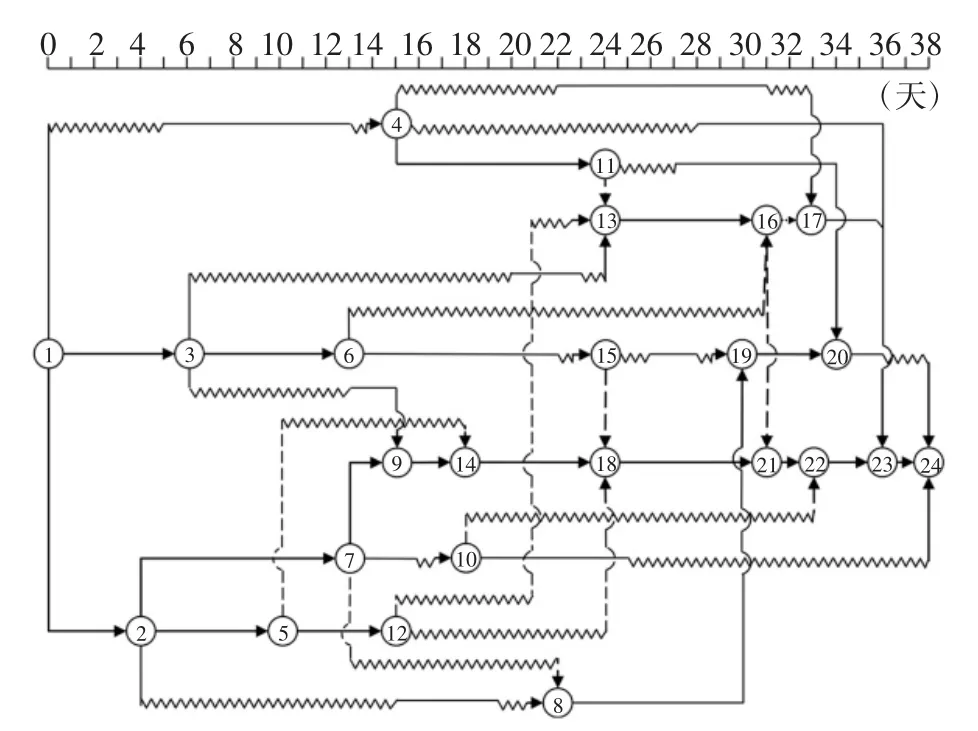
图9 优化后算例的双代号时标网络图Fig.9 The activity-on-arc time scaled network after optimization

为检验基于子集模拟的建议优化算法的稳定性，表3 给出了建议优化算法100 次独立运行求解后的统计结果.目前，针对资源均衡问题的启发式算法间的对比研究较少，学界对各种启发式算法的优劣未达成共识.同时，遗传算法因其自行概率搜索、运算并行性、应用不依赖问题种类的强鲁棒性等特点，在资源均衡问题中应用更为广泛[16-18].因此，本文选择遗传算法进行对比分析，与其他启发式算法的对比分析，将在后续的研究中进行.表3 提供了遗传算法（Genetic Algorithm，GA）100 次独立运行求解后的统计结果.考虑到交叉概率参数pc和变异概率参数pm对GA 算法求解的影响，本文依据两个参数的一般取值范围，进行了大量pc和pm组合取值下GA 算法的性能检验.检验发现，交叉概率pc=0.2 和变异概率pm=0.015 下GA 算法求解本算例多资源均衡问题的性能最优，因此表3 给出的是这组交叉概率和变异概率下GA 算法的对比结果.同时，考虑到计算资源对两种优化算法的影响，两种优化算法中每代的样本数均取2 000，迭代次数均取30 代.

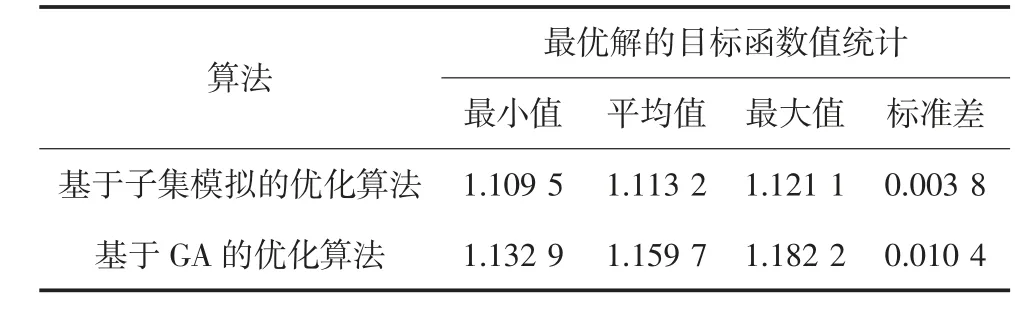
表3 基于子集模拟的优化算法与GA 算法独立运行100 次获得的最优目标函数值的统计结果Tab.3 Statistical results of 100 independent runs using subset simulation-based proposed algorithm and GA

表3 提供了两种算法100 次独立运行求解获得的最优解的目标函数值的统计结果（最小值、平均值、最大值及标准差）.对比可知，基于子集模拟的优化算法获得最优目标函数值的平均值为1.113 2，小于基于GA 的优化算法的相应数值（1.159 7）.同时，基于子集模拟的优化算法获得最优解的目标函数值的最大值（最差情况下）为1.121 1，小于基于GA 的优化算法获得最优解的目标函数值的最小值（最好情况下）1.132 9，且最优目标函数值的标准差更小.此外，图10 给出了两种算法100 次独立运行获得的最优解的目标函数值的分布情况.由图10 可见，基于子集模拟的优化算法性能更优，其获得的最优目标函数值更小，且分布更为集中，有93%的最优目标函数值集中在[1.109，1.119]区间，表明基于子集模拟的建议优化算法获取最优解的稳定性更高.

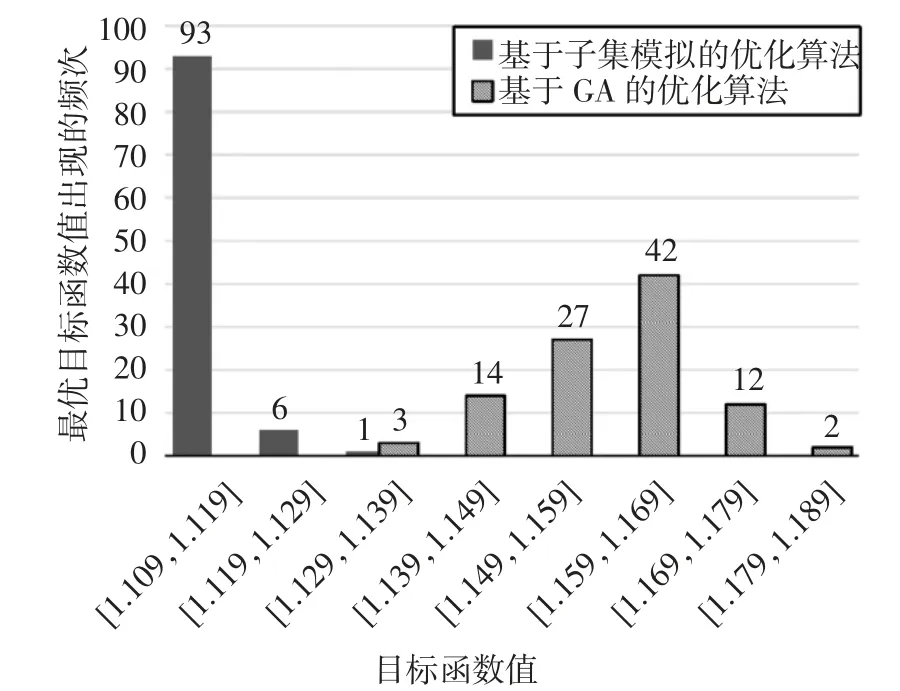
图10 两种优化算法独立运行100 次获得的最优目标函数值的分布Fig.10 Distribution of the optimal objective function value from 100 independent runs of using subset simulation-based proposed algorithm and GA

5 结论

本文针对建设工程项目的多资源均衡优化问题，基于子集模拟法进行启发式优化算法的研究，主要研究结论如下：

1）在构造建设工程项目多资源均衡优化模型时，引入间隔率变量，并在间隔率变量和工序计划开始时间的映射中考虑工序间逻辑关系，以避免工序逻辑关系违反时复杂修复算子的使用.

2）针对间隔率变量表示的建设工程项目多资源均衡优化模型，提出基于子集模拟的建议优化算法，并给出算法框架和具体操作步骤.

3）通过算例验证，与应用较广的遗传算法相比，基于子集模拟的建议优化算法在最优解的获取稳定性上有较大改进.