预应力钢板带加固砖砌体墙抗震性能试验研究

敬登虎，乔墩，邢凯丽

（东南大学 土木工程学院，江苏 南京，211189）

砌体材料的抗拉、抗剪强度较低，且整体性也较差.在砌体结构房屋的震害中，墙体的破坏问题比较突出[1-3]，主要表现为：墙体出现水平裂缝、斜裂缝、“X”形剪切裂缝、角部压碎、平面外倒塌等[4-6].因此，对砌体墙进行加固以提高其抗震性能显得尤为重要.

Eslamlou 等[7]对砌体墙的各种加固方法进行了总结，主要有纤维增强复合材料（FRP）包裹、嵌筋、钢筋混凝土面层、锚固钢板带、聚丙烯带包裹、钢丝水泥面层、钢索加固等方法；在这些方法中，FRP 容易发生剥离破坏；钢筋混凝土面层加固法和钢丝水泥面层加固法施工的湿作业时间长，并且需要一定时间进行养护.钢板带加固方法除了具有经济性好、质量轻、湿作业少、易于安装和拆除等特点，又能够充分提高被加固墙体的承载能力和变形能力.同时，砌体墙可为钢板带提供侧向支承，改善钢板带的局部屈曲现象.因此，采用钢板带对砌体墙进行加固有较大的潜力.Taghdi 等[8]进行了对拉螺栓锚固钢板带双面加固混凝土砌块砌体墙抗震性能的试验研究，结果表明加固后墙体的延性、刚度和耗能能力均得到了提高.Farooq 等[9-12]进行了改变钢板带参数加固砖砌体墙抗震性能的研究，结果表明影响加固效果的因素有用钢量、钢板带网格大小以及钢板带布置形式.于江等[13]、张广泰等[14]对格构式钢板带加固砖砌体墙的抗震性能开展了一系列试验研究与分析工作，证实格构式钢板带加固方法可有效地改善墙体的抗震性能.但是，常规的钢板带加固属于被动的加固模式，后布置的钢板带存在明显的应力滞后问题.Farooq 等[10]的研究发现，加固墙体达到破坏状态时，横、竖向钢板带都因为应力滞后难以充分利用材料性能，同时墙体的严重变形又加剧了钢板带的局部屈曲.

为此，本课题组提出了一种预应力钢板带加固砖砌体墙技术，即在砖砌体墙两面布置横、竖向钢板带，横向钢板带布置在墙面的内侧，两面的钢板带和墙体之间通过对拉螺栓进行锚固连接.对拉螺栓的紧固使得钢板带发生轴向变形，以此在钢板带中施加预应力，实现加固模式由被动转为主动，提高钢板带加固在正常使用状态下的利用效率.根据本课题组已完成的轴心受压性能研究[15]，预应力钢板带可有效地提高墙体的开裂荷载和峰值荷载.在此基础上，课题组开展了预应力钢板带（此处仅在横向钢板带中施加预应力）加固砖砌体墙的抗震性能试验研究.

1 试验概况

1.1 试件设计

本试验共设计了5 片墙体，其中UW 为普通砖砌体墙；试件SW1 采用预应力钢板带进行加固，并与试件UW 形成对比，用于研究预应力钢板带加固砖砌体墙的加固效果.试件SW2、SW3、SW4 分别改变了横向钢板带的预应力水平、墙体竖向负荷水平和墙体高宽比，以此研究上述参数对加固效果的影响.试件设计参数与制作详图见表1 和图1 所示.

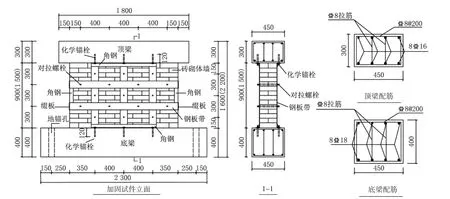
图1 试件设计详图Fig.1 Design details of specimens

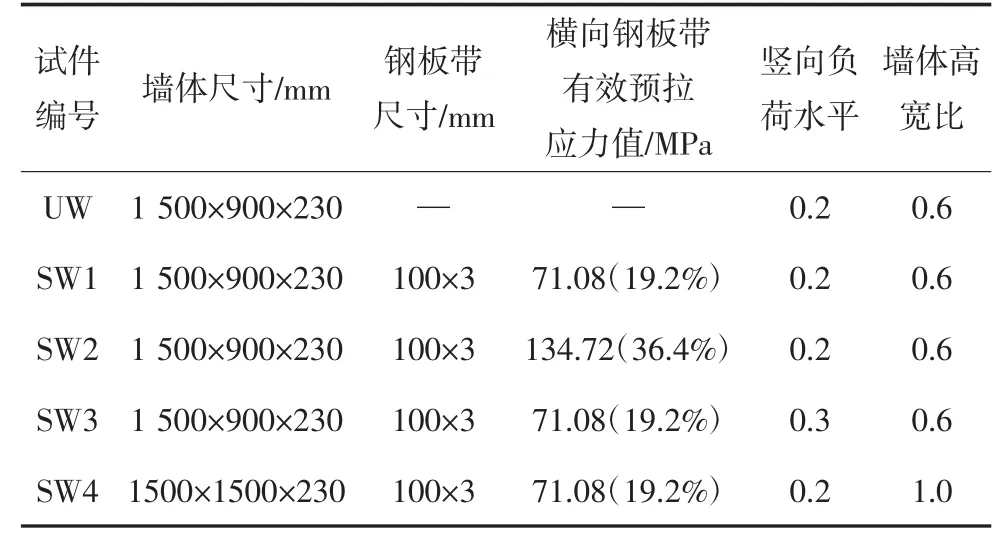
表1 试件参数汇总Tab.1 Summary of specimens’parameters

试件所用的烧结普通砖尺寸为230 mm × 100 mm×45 mm，强度等级为MU25，砂浆强度等级为M5.0；顶梁与底梁所用的混凝土强度等级为C30，钢筋等级为HRB400 级；加固中使用的钢板牌号为Q235，对拉螺栓采用6.8 级M14.

1.2 试件加固

预应力钢板带加固墙体的具体步骤和要点如下：1）按照对拉螺栓设计位置分别在墙体及钢板带相应位置钻取孔洞.其中，横向钢板带上的孔洞呈长圆形，以便拧紧对拉螺栓时钢板带可以单向滑动，从而在横向钢板带中产生较均匀的预拉应力.2）在砌体墙表面安装竖向钢板带，竖向钢板带上下端与水平角钢（⎿50×5）焊接，再用化学锚栓M12 将水平角钢分别与顶梁及底梁连接，锚栓锚固深度为120 mm.3）在竖向钢板带外侧安装横向钢板带.其中，试件SW2 在横向钢板带与竖向钢板带正交叠合处增设厚度为3 mm 的钢板垫块（图2），以便获得更高的预应力水平.墙体两侧面设置宽度为100 mm 的钢缀板，横向钢板带与钢缀板通过垂直角钢（⎿50×5）焊接，最终形成如图3 所示的闭合约束.4）拧紧横向钢板带上的对拉螺栓，使其产生拉伸变形从而在钢板带中获得预拉应力.此处，横向钢板带中预拉应力控制通过应变片实测取平均值，具体数值见表2.需要强调的是，考虑拧紧螺栓在横向钢板带中产生的局部效应原理（圣维南原理），实测的应变片位于横向钢板带与竖向钢板带正交叠合处外表面，该应变包含弯曲变形部分.

图2 试件SW2 钢板带正交叠合处细节Fig.2 Crossing details of specimen SW2's steel strips

图3 钢板带安装完成Fig.3 Installation of steel strips

表2 横向钢板带预应力实测值与理论值对比Tab.2 Comparison between measured and theoretical values of pre-stress in lateral steel strips

1.3 理论预应力值计算

横向钢板带的变形可简化为图4 所示的区段，图中OAB（O1A1B1）区域近似视为直角三角形.此外，考虑BB1段的弯曲变形，该段弯曲近似按圆弧考虑，且与两端相连线段相切.基于几何变形条件，横向钢板带与竖向钢板带正交叠合处外表面理论预拉应变（ε）可用式（1）进行计算：

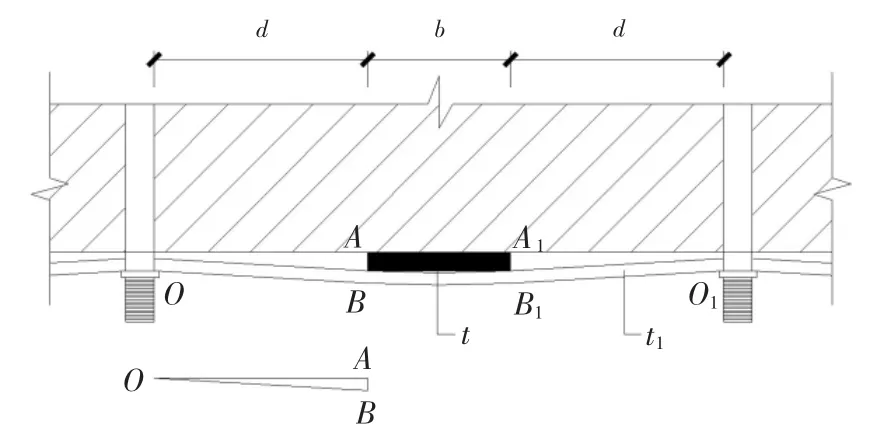
图4 预拉应变计算示意图Fig.4 Schematic diagram of calculating pretension strain

式中：t1为横向钢板带厚度；t2为对拉螺栓的张拉深度（线段AB 长度），该值不大于竖向钢板带厚度，本试验中对于试件SW2 取4.5 mm，其余试件均取3.0 mm；d 为对拉螺栓边缘与竖向钢板带边缘的距离；b为竖向钢板带的宽度.表2 对比了横向钢板带与竖向钢板带正交叠合处表面的理论预应力值与实测值，其中钢板的弹性模量取206 GPa，可见式（1）具有较好的预测精度.此时，横向钢板带中的有效预拉应力计算应扣除弯曲变形对实测应变的贡献，即可按钢板带厚度中心线计算拉伸应变（εe），可得到式（2）；各试件中横向钢板带的有效预拉应力值见表2.需要注意的是，当t1或t2较大时，施加预拉应力的难度明显增加，在实际工程应用时，该值不宜过大.

1.4 材料性能

依据我国现行相关材料性能试验方法[16-18]，所用主要材料实测强度如下：MU25 实心烧结普通砖的抗压强度平均值为27.6 MPa；M5.0 级砂浆的抗压强度平均值为5.14 MPa；3mm 厚Q235 钢板的屈服强度平均值为370.0 MPa，极限抗拉强度平均值为515.6 MPa；M14 级对拉螺栓的抗拉强度平均值为694.5 MPa.

1.5 试验加载及测量内容

试验加载装置见图5，试验过程中使用油压千斤顶施加竖向荷载后恒定，使用水平作动器施加水平荷载模拟地震作用.为了保证竖向荷载均匀施加在墙体顶部，在千斤顶与压顶梁之间设置两个正交的分配梁，并在分配梁间设置滚轴小车，以此保证试验中竖向荷载不会因为墙体位移而改变方向.根据试件设计负荷水平以及同批对比试件实测的砌体强度[15]，试件SW3 所施加的竖向荷载为690 kN，其余试件所施加的竖向荷载为460 kN.

图5 试验装置Fig.5 Test set-up

水平荷载采用逐级加载的方式，墙体开裂前按荷载控制，每级按20 kN 递增，每级循环1 次，持荷3 min 后进行测量记录；当墙体出现贯穿3 皮砖长的裂缝时认为墙体开裂；开裂后，以开裂位移的倍数作为级差进行位移控制加载，每一级循环3 次；当试件承载力降至85%峰值荷载时，认为达到极限状态，停止试验.

图6 为试件SW1～SW3 中钢板带上的应变片正面位置，反面与此对称（SW4 与此类似），其中横向钢板带上应变片布置在横、竖向钢板带正交叠合处正中，另外布置一组应变片在横、竖向钢板带叠合边缘与对拉螺栓中间位置，由此记录不同区段钢板带表面的应变情况.试验过程中，所施加的水平荷载及相应位移由加载系统自动采集.

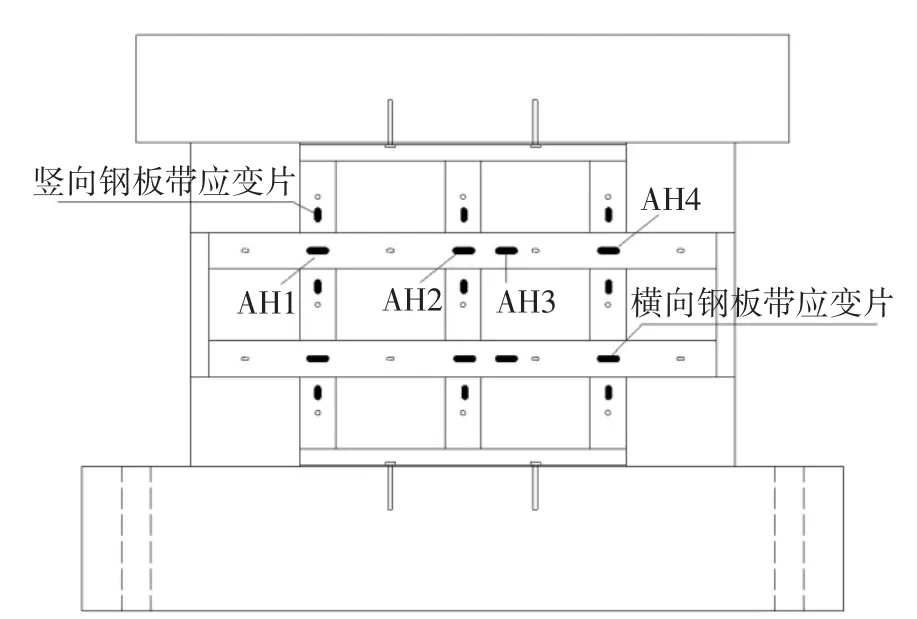
图6 应变片布置Fig.6 Configuration of strain gauges

2 试件破坏过程

2.1 试件UW

当水平荷载加到220 kN 时，墙体左上角出现一条贯穿3 皮砖长的裂缝，对应的开裂位移Δc=2 mm.当位移加到Δc时，墙体顶部出现细小斜裂缝.当位移加到2Δc时，原有裂缝沿着墙体顶部约50°方向往下延伸并贯穿全墙，同时出现了一条与其对称的新的裂缝.当位移加到3Δc时，墙体有少量砖起皮脱落，随后墙体上原有裂缝宽度急剧增大，并在墙顶中部出现新的斜向长裂缝，荷载迅速下降至峰值荷载的85%以下，试件达到极限状态（图7）.此处，墙体的破坏形态表现为剪切破坏.

图7 试件UW 破坏形态Fig.7 Failure mode of specimen UW

2.2 试件SW1

当水平荷载加到280 kN 时，墙体的顶部出现了一条贯穿3 皮砖长的裂缝，此时对应的开裂位移Δc=3.6 mm.当位移加到Δc时，墙顶细微裂缝增加.当位移加到2Δc时，原有裂缝拓展延伸，并新出现一条从墙顶贯穿至墙体左下角的斜裂缝.当位移加到3Δc时，右侧一条裂缝出现分支，其中一支沿灰缝水平延伸，另一支向右下角延伸并贯穿全墙.墙体角部砖块出现压碎现象.当位移加至4Δc时，砖块持续压碎、脱落.墙体上斜裂缝进一步延伸、变宽.当位移加到5Δc时，墙体角部砖块严重碎裂，部分竖向钢板带出现局部弯曲（图8（a）），墙体裂缝明显可见（图8（b）），试件达到极限状态.此处，墙体的破坏形态表现为弯剪破坏.

图8 试件SW1 破坏形态Fig.8 Failure mode of specimen SW1

2.3 试件SW2、SW3

试件SW2、SW3 的破坏过程类似于SW1，但开裂点、峰值点以及极限点的位移与荷载有所差异，具体详见表2 所示，在此不再赘述.两个试件中墙体的破坏形态均表现为弯剪破坏（图9、图10）.

图9 试件SW2 破坏形态Fig.9 Failure mode of specimen SW2

图10 试件SW3 破坏形态Fig.10 Failure mode of specimen SW3

2.4 试件SW4

当水平荷载加到240 kN 时，墙体角部出现3 皮砖长细微裂缝，对应的开裂位移Δc=4.5 mm.当位移加到3Δc时，墙体右下角出现一条竖向裂缝，左下角出现一条水平裂缝.当位移加到5Δc时，裂缝进一步发展，墙体角部出现脱空现象.当位移加到7Δc时，墙体角部压碎现象严重，竖向钢板带出现局部弯曲，但墙体表面无明显的斜向裂缝（图11）.此处，墙体的破坏形态表现为弯曲破坏.

图11 试件SW4 破坏形态Fig.11 Failure mode of specimen SW4

在本试验研究中，水平荷载是直接作用在顶部混凝土梁上，混凝土梁底与墙体顶部之间（矩形截面）产生剪应力，剪应力分布形式为中部大、两端小.此外，墙体顶部的竖向压应力近似均匀.在这种压应力和剪应力共同作用下，砖砌体墙在发生与剪切相关的破坏形态时，则表现出图7～图10 所示的“八字形”裂缝分布特征.

3 抗震性能分析

3.1 滞回曲线

滞回曲线是结构在往复荷载作用下的荷载-位移曲线，能够全面反映试件的抗震性能.各个试件的滞回曲线如图12 所示，可以看出：1）试件UW 的滞回曲线在加载初期基本呈线性，然后很快就到达了极限状态，滞回环包围的面积较小.2）加固试件的滞回曲线都存在“捏缩”现象；试件SW1 的滞回曲线呈弓形，与试件UW 相比滞回曲线的形状更加饱满，能达到的加载级数和峰值荷载也明显大于UW；试件SW2、SW3 滞回曲线饱满程度要小于SW1，但有更大的峰值荷载；试件SW4 滞回曲线呈Z 形，曲线形状不饱满，但较SW1 有更大的极限位移.

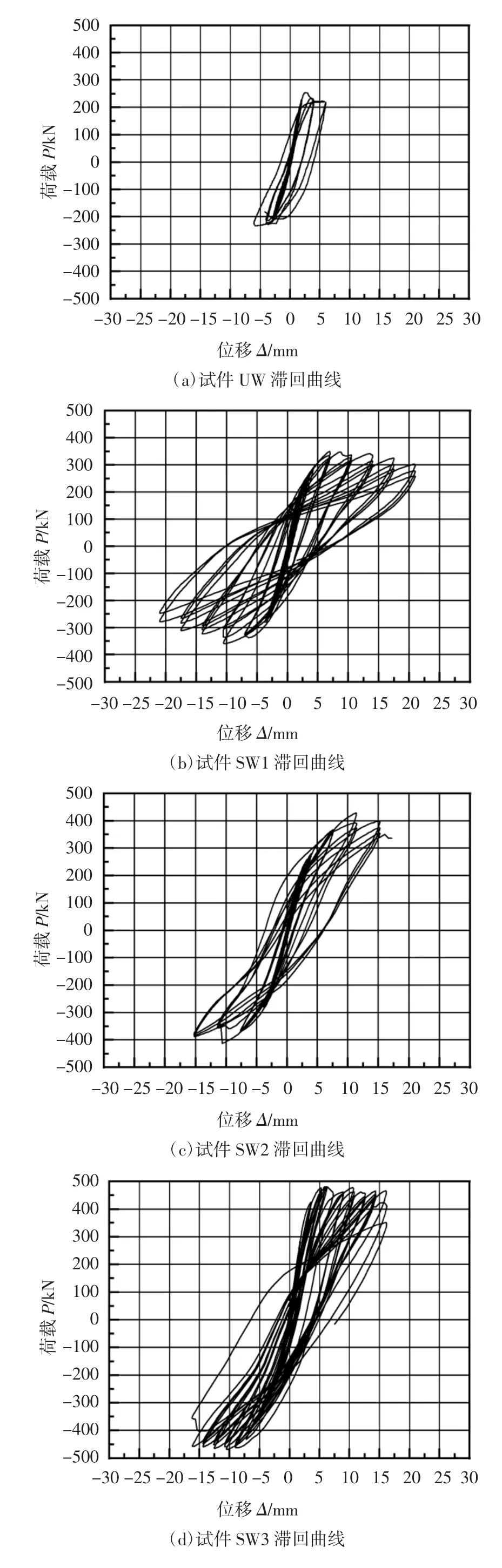
图12 试件滞回曲线Fig.12 Specimens’hysteretic curves

3.2 骨架曲线

将滞回曲线上每一级加载首次循环所对应的荷载峰值点相连可以得到试件的骨架曲线，通过骨架曲线可以确定试件的抗侧刚度、承载能力和延性等特征.5 片墙体的骨架曲线汇总如图13，试验结果汇总见表3.取峰值荷载Fmax的85%为极限荷载Fu，极限荷载对应的位移即为极限位移Δu[19].位移延性系数μ 采用极限位移Δu和屈服位移Δy之比进行计算.本文采用如图14 所示的能量等值法[20]确定试件的屈服荷载Fy和屈服位移Δy.

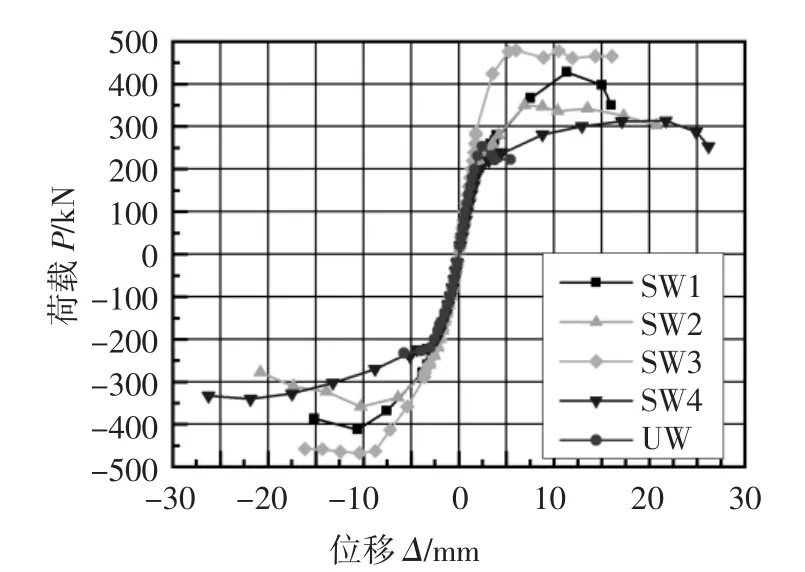
图13 试件骨架曲线Fig.13 Specimens’skeleton curves

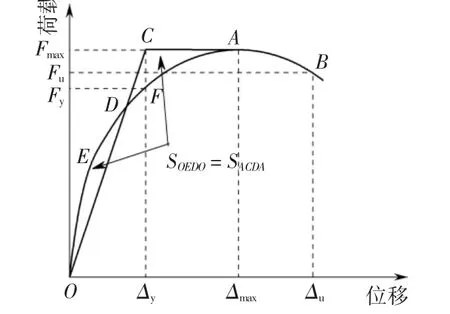
图14 屈服位移确定方法Fig.14 Determination method of the yield displacement

由表3 可知，与未加固试件UW 相比，SW1 开裂点的抗侧刚度下降了29.3%，这主要是因为横向钢板带的约束作用延缓了裂缝的形成和开展.试件SW1 峰值承载力提高了45.5%，延性提高了76.4%，表明使用预应力钢板带能够显著提高砖砌体墙的承载能力和变形能力.

表3 试验结果汇总Tab.3 Test results

试件SW2 与SW1 相比，横向钢板带中有效预应力水平提高了89.5%（达到屈服强度的36.4%）.此时，试件SW2 的开裂点抗侧刚度与SW1 几乎相同，峰值承载力提高了18.3%，延性下降了44.0%.由此可见，横向钢板带中预应力水平对试件的初始抗侧刚度几乎无明显影响，由于横向钢板带中应力水平提升，钢板带对试件的裂缝发展限制作用增强，提高了屈服位移和承载力，但延性有所下降.

试件SW3 较SW1 仅提高了墙体竖向负荷水平，开裂点抗侧刚度较SW1 提高了近1 倍，峰值承载力提高了33.5%，延性下降了23.1%.这是因为增大竖向压力可提高墙体中砌块与砂浆间的摩擦阻力，减小墙体的变形能力.

试件SW4 与SW1 相比提高了墙体的高宽比，开裂点抗侧刚度下降了31.5%，峰值承载力和延性略有下降.这是因为试件SW4 中墙体的破坏形态为弯曲破坏，钢板带的加固效果较差.

3.3 横向钢板带应变发展规律

限于篇幅，选取了有代表性的试件SW1 中上面横向钢板带各区段（图6）应变实测值进行分析.从图15 可以看出，各应变片的初始值（预拉应变）存在一定差异，这是由于钢板带各区段的拉伸变形存在安装误差与摩擦力，预拉应力并非理想的均匀分布.在加载前期，应变数值变化幅度较小，基本不变.当荷载施加到280 kN 时，墙体开裂后，横向钢板带进行二次受拉，应变总体开始呈升高趋势，但不同位置的变化幅度并不相同.在达到极限状态时，此条钢板带的实测应力均值为173 MPa，扣除弯曲部分的影响后，有效拉伸应变可达0.07%.此时，钢板带中的有效拉应变比文献[10]中常规正交钢板带加固在极限状态时的0.01%～0.06%至少提高了16.7%，即横向钢板带中施加预拉应力能够有效提高钢板带的材料利用率.

图15 SW1 横向钢板带应变发展Fig.15 Strain development of SW1’s lateral steel strips

3.4 预应力控制建议

由表3 可知，随着横向钢板带中预拉应力的增加，并非各项指标都得到提高.此处，定义φ 为横向钢板带中的预拉应力特征值，按照公式（3）进行计算.式中，b1、t1为横向钢板带宽度、厚度；σps为横向钢板带中有效预拉应力平均值，由式（2）得到的应变乘以钢板的弹性模量进行计算；bm为横向钢板带有效约束宽度，可取计算横向钢板带上下区格墙面高度的1/2；tm为砌体墙厚度；fm为砌体轴心抗压强度平均值，按式（4）计算[21]，f1、f2分别为砖和砂浆的抗压强度平均值；系数k1、α 对于烧结普通砖取值为0.78 和0.5；k2对于烧结普通砖，且砂浆强度不低于1 MPa时，取值为1.0.

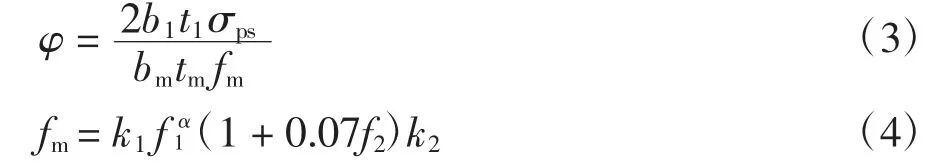
提高横向钢板带中的有效预拉应力，预拉应力特征值φ 也会提高.基于后期的有限元数值模拟补充分析，发现随着φ 的提高，加固墙体的水平承载力出现先增大后降低现象.当φ 值取为0.169 时，加固效果较好，实际工程中建议按此值进行控制.

3.5 抗剪承载力计算

加固后试件的破坏机理复杂，其抗剪承载力（V）可简化为砖砌体（Vm）、横向钢板带（Vs）二者所承受水平力的叠加，如式（5）所示.Vm采用式（6）进行计算[22]，其中Aw为墙体的水平截面积，σy为压应力，fv0为σy=0 时对应的砌体抗剪强度，可根据式（7）进行计算[23].式（7）中k5为与砌体种类相关的系数，烧结普通砖取0.125；f2为砂浆抗压强度平均值.鉴于横向钢板带在施加了一定预应力后，其应力只在临近极限状态时总体上有较明显的增长，在峰值点状态时应力增长较小.此外，结合文献[12-14，24-25]中常规正交钢板带、嵌筋加固砖砌体墙的试验研究结果，加固用材料在试件峰值点状态时的应力约为其屈服强度fy的15%.因此，Vs可由式（8）近似确定；其中，As为横向钢板带的截面面积之和；σe取为σps与0.15fyAs两者中的较大值.

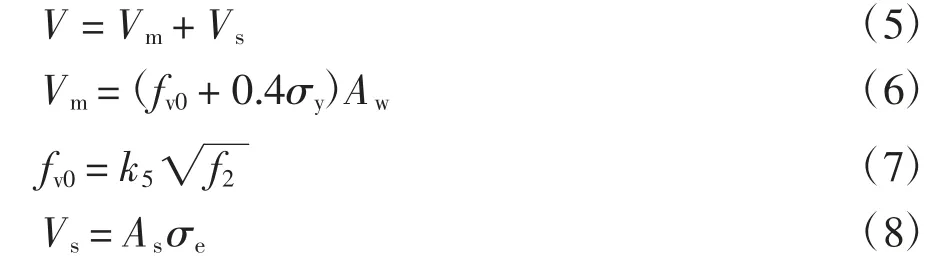
依据公式（5）～（8），试件UW、SW-1～SW-3 的抗剪承载力计算值与实测值之比分别为1.15、1.03、1.05 和0.97.由此可见，上述计算方法具有较好的预测精度.

4 结论

1）使用预应力钢板带加固的试件SW1 相较未加固试件，破坏形态由剪切破坏转变为弯剪破坏，开裂点抗侧刚度下降了29.3%，峰值承载力提高了45.5%，延性提高了76.4%.因此，采用预应力钢板带对砖砌体墙进行抗震加固效果明显.

2）当横向钢板带中的预拉应力水平提高至屈服强度的36.4%时，试件的开裂点抗侧刚度几乎没有变化，峰值承载力提高了18.3%，但延性下降了44.0%.

3）当墙体的竖向负荷水平提高至0.3 时，墙体的开裂点抗侧刚度提高了近1 倍，峰值承载力提高了33.5%，但延性有所下降.

4）当墙体的高宽比提高至1 时，开裂点抗侧刚度下降了31.5%，峰值承载力和延性有小幅下降.相比其他加固试件，加固效果相对较差.

5）加载前期，横向钢板带中应力值基本不变；墙体开裂后，横向钢板带的应变总体开始呈升高趋势；横向钢板带施加预拉应力后，材料的利用率得到提高.当预应力特征值取为0.169 时，加固效果较好.

6）提出了预应力钢板带加固砖砌体墙的抗剪承载力计算方法，并具有较好的预测精度.