钢筋混凝土牛腿抗剪承载力设计修正系数研究
黄远,尹文萌,易伟建1,
(1.湖南大学 工程结构损伤诊断湖南省重点试验室,湖南 长沙 410082;2.湖南大学 土木工程学院,湖南 长沙 410082)
钢筋混凝土牛腿被广泛应用于装配式混凝土结构中预制构件之间的铰接连接[1].例如工业厂房的预制混凝土柱牛腿,用于支承吊车梁、屋架及墙梁等水平构件.牛腿用于构件连接其施工非常便捷,但是在荷载作用下,牛腿的受力状态较为复杂,类似于变截面深梁,在国际上通常将钢筋混凝土牛腿归为“D区”(Discontinuity Zone)构件.牛腿的剪切破坏通常为脆性破坏,时常造成重大人员伤亡和经济损失.
目前国内外对牛腿抗剪承载力进行了较为系统的研究.我国高丹盈等人[2-4]开展了一系列的牛腿受剪试验,研究了不同钢纤维体积率、剪跨比、配筋率等参数条件下的牛腿受剪性能,并根据试验数据提出了牛腿承载力的计算方法.国外的研究人员在早期的桁架模型基础上进行完善,提出了拉压杆模型(简称STM),并使之成为一种通用的设计方法[5].随后,学者们基于传统的STM,考虑了混凝土的软化效应,提出了更深入的计算理论.Hwang 等[6]提出了软化拉压杆模型(简称SSTM),通过迭代计算混凝土软化系数,考虑开裂钢筋混凝土的本构关系和相容方程.Russo 等[7]通过拟合试验数据简化了混凝土软化系数的计算公式.SSTM 能准确预测D 区构件的承载力[8-9].
牛腿受剪机理的复杂性也体现在规范层面,不同于正截面受弯承载力的统一力学模型,各国规范中牛腿受剪承载力计算公式的表现形式和所考虑的参数影响有很大的区别.我国规范[10]基于三角桁架抗弯模型,ACI 318-19[11]、EC2[12]、CSA A23.3-04[13]主要基于STM.各规范设计公式的计算结果与试验数据均存在一定程度上的离散性.因此,需要对规范公式的适用性进行评估和深入研究,为工程设计提供理论指导.
文章首先介绍了ACI 318-19[11]、EC2[12]、CSA A23.3-04[13]三国规范基于拉压杆的牛腿承载力计算方法和SSTM[6]、Russo 等[7]两种主要的牛腿承载力计算模型.采用209 组牛腿竖向受剪试验数据评估了各承载力计算模型的准确性和安全性.在此基础上,按照我国规范设计了一系列不同参数条件下的钢筋混凝土牛腿,基于SSTM[6]研究各设计参数对牛腿抗剪承载力的影响.最后依据参数分析的结果,提出了牛腿抗剪承载力修正系数的简化公式,为工程实际提供参考.
1 牛腿承载力计算模型
1.1 国外规范拉压杆模型
拉压杆模型(简称STM)由一定强度的钢筋拉杆、混凝土压杆和混凝土节点组成.牛腿作为典型的“D 区”构件,ACI 318-19[11](以下简称ACI)、EC2[12]、CSA A23.3-04[13](以下简称CSA)三国规范均采用STM 对其进行设计.ACI STM 适用于剪跨比不大于2的牛腿,规范限制压杆水平方向倾角θ 不小于25°;EC2 STM 和CSA STM 适用于简跨比不大于1 的牛腿,EC2 STM 对压杆水平倾角θ 的限制条件为1≤tanθ ≤2,CSA STM 对压杆角度θ 未给出限制条件.
文章参照文献[14]对牛腿建立了理想的STM,符合各规范要求,用于评价ACI、EC2、CSA 牛腿承载力计算方法.如图1 所示,A、A′节点水平位置为承压平台中心,A、A′节点竖向位置为纵向受拉钢筋形心;B、B′水平位置为中柱1/4 宽度处,B、B′竖向位置为牛腿根部截面按塑性抗弯理论确定的等效矩形压应力分布图的中心.三国规范STM 的主要区别在于混凝土压杆和混凝土节点强度的确定方法不同,它们关于混凝土抗压强度有效系数β 的取值见表1.表中βc为混凝土强度有效系数,ρsv为箍筋配筋率,θ为混凝土压杆与水平方向的夹角,fc为圆柱体抗压强度,ε1为压杆的横向拉应变.
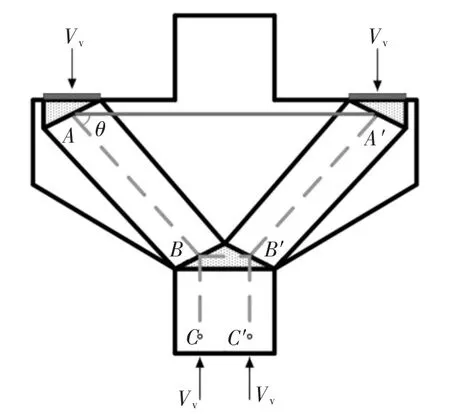
图1 拉压杆模型Fig.1 Strut-and-tie model

表1 规范STM 混凝土抗压强度有效系数β 取值Tab.1 Concrete efficiency coefficient β of standard STM
1.2 软化拉压杆模型
Hwang 等[6]在2000 年首次提出了软化拉压杆模型(简称SSTM),该模型考虑了开裂钢筋混凝土的平衡方程、本构关系和相容方程.图2 为按SSTM 计算牛腿竖向承载力的简图,图中θ 为对角混凝土斜压杆与水平方向的夹角,θs为两侧混凝土斜压杆与水平方向的夹角;a 为竖向剪力Vv至牛腿根部截面的水平距离,h 为对角线混凝土压杆的高度;水平箍筋拉杆定位于h/2 处,力的大小用Fh表示;Vh为牛腿受到的水平力,D 为对角线混凝土斜压杆的内力(定义压力为负值),Cd为节点区域混凝土的压力.在牛腿中SSTM 存在两种抗剪机制,斜向机制和水平机制.斜向机制是由对角混凝土斜压杆组成,水平机制是由水平箍筋拉杆和两侧混凝土斜压杆组成.牛腿受到的竖向剪力Vv由混凝土和水平箍筋共同承担.SSTM 的承载力计算状态为节点区域最大应力达到混凝土的极限抗压强度,计算过程较复杂需要迭代求解.

图2 软化拉压杆模型Fig.2 Softend strut-and-tie model
1.3 Russo 等拉压杆模型
Russo 等[7]在2006 年提出了考虑开裂钢筋混凝土平衡方程、本构关系和相容方程的简化拉压杆模型(简称Russo STM),该模型也存在两种剪力传递机制.第一种剪力传递机制为牛腿水平纵筋和腹部混凝土构成的压杆机制,第二种是由水平箍筋提供的水平桁架机制,其承载力计算公式如下:

其中χ 代表简化的混凝土软化系数,计算式如下:

2 牛腿受剪承载力计算方法评价
2.1 牛腿受剪试验数据库
文章共收集了209 组竖向受剪不带纤维的钢筋混凝土牛腿试验数据,称为牛腿总评价数据库.用于评价国外规范STM、SSTM 以及Russo STM.这些数据来源于试验文献[3,14-24],包含了牛腿剪切破坏、斜压破坏等主要的破坏模式,剔除了承压破坏、锚固破坏等次要的破坏模式.为准确评价ACI STM、EC2 STM 及CSA STM,用于评估的牛腿试验数据还需满足以下准则:1)给出承压垫板宽度;2)压杆水平倾斜角θ≥25°;3)压杆水平倾斜角θ 满足1 ≤tan θ ≤2.
CSA STM 未限制压杆角度θ,仅需满足准则1,总评价数据库筛选后还剩180 组数据,称为STM 评价数据库;ACI STM 需满足准则1、2,评价数据库筛选后仍有180 组数据,与STM 评价数据库同;EC2 STM 需满足准则1、3,评价数据库筛选后还剩124组数据,称为EC2 STM 评价数据库.STM 评价数据库中不满足规范的数据计算过程不变但是不参与评价EC2 的统计分析.
2.2 计算方法评价
为了评价各个承载力计算模型的准确性和安全性,本文定义了计算模型误差系数η 和安全度n.计算模型误差系数η 是承载力试验值Vt与承载力计算值Vc的比值,η 越接近1 表明承载力计算值越接近承载力试验值.ηm、ηcov分别为计算模型误差η 的平均值和变异系数.ηm越接近1 表明承载力计算模型越准确,ηcov值越小表明承载力计算结果离散性越小.安全度n 为η 值大于1 的试件数与总试件数的比值,象征着承载力计算模型的安全性,n 值越大表明承载力预测结果越安全.
各承载力计算方法的评价结果见表2.对于EC2 STM 评价数据库124 组牛腿数据,EC2 ηm值为1.56,n 值为96%,承载力预测结果较准确安全;ηcov值为0.26,在规范计算方法中变异系数最低.由表2 还可知,与无箍筋牛腿相比,对于带箍筋牛腿,CSA STM和EC2 STM 规范ηm计算值均明显偏大即承载力计算值明显偏小,这说明了规范低估了箍筋对牛腿的抗剪承载力贡献.

表2 牛腿各承载力计算方法的评价结果Tab.2 Results of calculation methods for bearing capacity of corbel
为进一步比较各承载力计算方法关于牛腿承载力计算的适用性,文章探究了牛腿关键参数对承载力预测结果的影响.这些参数分别为:混凝土抗压强度fc,剪跨比a/d,纵筋配筋率ρf和箍筋配筋率ρs.图3~图7 为各承载力计算方法的预测效果图,图的横坐标为牛腿各主要参数,纵坐标为计算模型误差η.
如图3(d)、图4(d)和图5(d)所示,当剪跨比a/d小于0.1 时,ACI、EC2、CSA η 值明显偏大,这说明了规范STM 模型对剪跨比极小的牛腿承载力预测值过于保守.如图3(d)、图4(d)所示,当剪跨比a/d 大于0.1 时,随着a/d 的增大,ACI、EC2 η 值呈降低的趋势,这说明ACI STM 和EC2 STM 在剪跨比较大时高估了牛腿的承载力.如图5(d)所示,当剪跨比a/d大于0.1 时,CSA STM 较好地反映了剪跨比a/d 对牛腿承载力的影响,这是因为CSA STM 混凝土压杆有效系数β 考虑到了压杆角度的影响.

图3 ACI 318-19 计算模型误差η 值随各参数的变化Fig.3 Calculation model error η of ACI 318-19 versus main parameters
如图3(a)和图5(a)所示,随着混凝土抗压强度fc的增大,ACI 和CSA η 值呈下降的趋势.当fc大于40 MPa 时,出现了部分η 值小于1 的数据,预测结果偏不安全,这说明了ACI STM 和CSA STM 不适用于计算高强钢筋混凝土牛腿.如图4(a)所示,EC2 STM 较好地反映了混凝土抗压强度fc对牛腿承载力的影响,这是因为EC2 STM 混凝土压杆有效系数β考虑了混凝土抗压强度的影响.

图4 EC2 计算模型误差η 值随各参数的变化Fig.4 Calculation model error η of EC2 versus main parameters

图5 CSA A23.3-04 计算模型误差η 值随各参数的变化Fig.5 Calculation model error η of CSA A23.3-04 versus main parameters
如图3(c)所示,在箍筋配筋率ρs小于0.3%时,ACI η 值偏高;在箍筋配筋率ρs大于0.3%时η 值较稳定.这说明了ACI STM 压杆有效系数β 考虑了箍筋配筋率ρs的影响,在ρs较大时能很好地反映箍筋的抗剪贡献,但在ρs较小时低估了箍筋的抗剪贡献.
与无箍筋牛腿相比,三国规范STM 模型计算得到的带箍筋牛腿η 值偏高,即承载力计算值偏小,并且剪跨比越小这种规律越明显.这说明了三国规范STM 模型低估了箍筋对于牛腿抗剪承载力的贡献,并且CSA STM 和EC2 STM 在剪跨比越小时这种情况越显著.
如图6 和图7 所示,SSTM 和Russo STM 两种模型均能很好地反映各主要参数对带箍筋牛腿和无箍筋牛腿抗剪承载力的影响.对于总评价数据库209组牛腿数据,SSTM ηm值为1.14,Russo STM ηm值为0.99,两种精细计算模型承载力计算值均与试验值吻合良好.SSTM n 值为77%,承载力计算结果安全性较好;Russo STM n 值为44%,超过半数以上的牛腿试件承载力计算值小于试验值,承载力预测结果偏不安全.
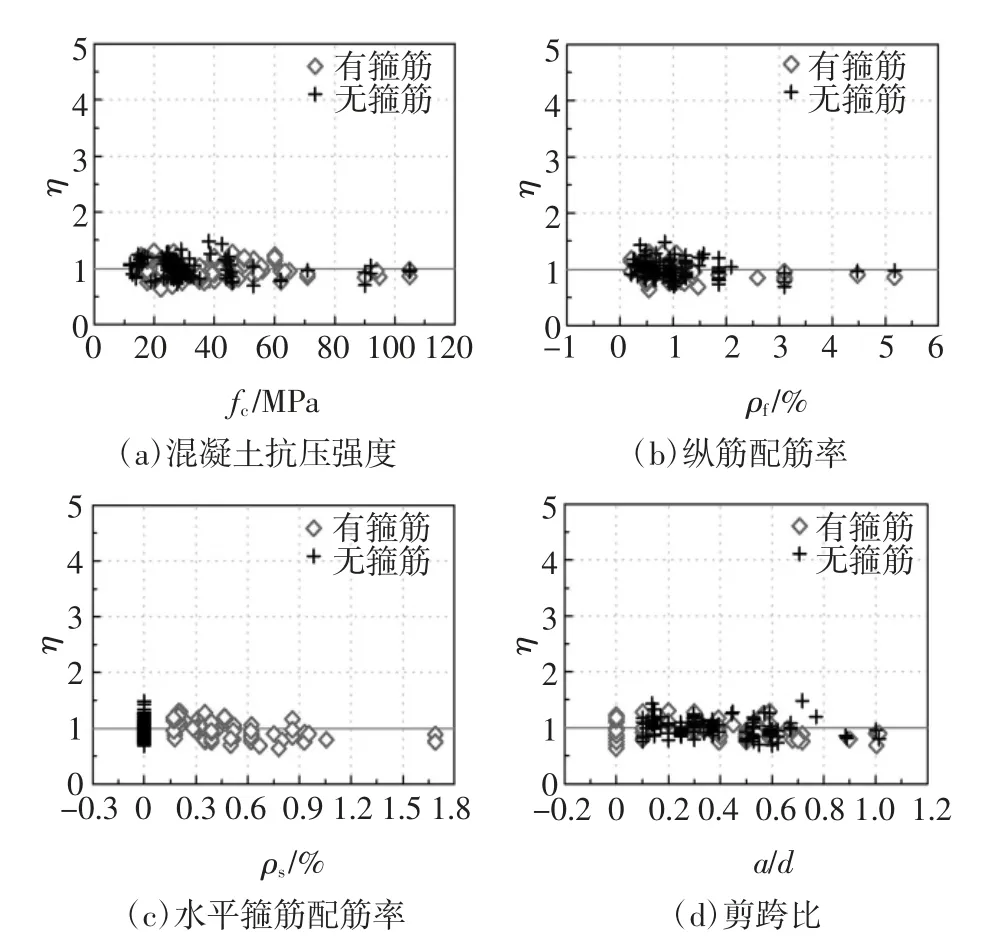
图7 Russo STM 计算模型误差η 值随各参数的变化Fig.7 Calculation model error η of Russo et al versus main parameters
综上所述,规范拉压杆模型的牛腿承载力计算方法偏于保守并且与试验数据对比离散性大,SSTM承载力计算的准确性和安全性均较好且能反映牛腿主要参数对承载力的影响.因此,文章接下来将以SSTM 为基准,对我国规范的牛腿设计方法进行分析,并给出实用设计建议.
3 我国规范评价
本节首先设计一系列满足《混凝土结构设计规范》(GB 50010—2010)(以下简称我国规范)要求的钢筋混凝土牛腿[10].我国规范是针对剪跨比不大于1的短牛腿设计.如图8 所示,其计算模型为三角桁架模型,将牛腿顶部水平纵筋理想成拉杆、腹部混凝土理想成压杆,竖向荷载由水平纵筋拉杆和混凝土斜压杆共同承担.牛腿所需纵向受拉钢筋面积如式(1).

式中:Fv为作用在牛腿顶部的竖向力设计值;fy为牛腿纵向受拉钢筋屈服强度;As为纵向受拉钢筋面积;h0为牛腿有效高度;av为竖向力作用点至下柱边缘的水平距离,为保证牛腿的承载力,当av≤0.3h0时,取av=0.3h0.
同时为了保证牛腿在使用阶段不出现斜裂缝,牛腿截面尺寸应满足式(2).

式中:b 为牛腿宽度;ftk为混凝土轴心抗拉强度标准值;Fvk为作用于牛腿顶部按荷载效应标准组合计算的竖向力值;β 为裂缝控制系数,对于支承吊车梁的牛腿取0.65;其余符号同上.
需要说明的是,我国规范只给出了牛腿受弯承载力的简化计算公式,牛腿的截面高度是根据使用荷载下的斜截面抗裂确定的.规范中没有给出牛腿抗剪承载力的计算公式,其隐含的意思是具有足够的受剪承载力,且不小于受弯承载力.为了评估我国规范的准确性和安全性,本文结合规范牛腿抗弯承载力设计公式(1)和牛腿斜截面开裂荷载标准值计算公式(2)得到我国规范牛腿设计剪力的计算公式(3).

选取的标准模型初始设计参数为:剪力设计值800 kN,混凝土强度等级C40,纵筋和箍筋均采用HRB400 钢筋,牛腿的宽度和剪切跨度分别为400 mm 和250 mm.将初始设计参数代入我国规范牛腿设计公式,可以计算得到牛腿的有效高度h0为765 mm,纵筋和箍筋面积分别为923 mm2和462 mm2.标准模型的尺寸和配筋如图9 所示.

图9 标准模型图Fig.9 Detail of standard model
然后在标准模型的基础上每次变化一个设计输入参数,包括设计荷载Fv、混凝土强度fc、纵筋屈服强度fy、箍筋屈服强度fyv、剪切跨度a 和牛腿宽度b,可以生成一系列满足我国规范要求的钢筋混凝土牛腿.参数取值范围参考常用工程变化范围[25-26],牛腿设计参数取值见表3.
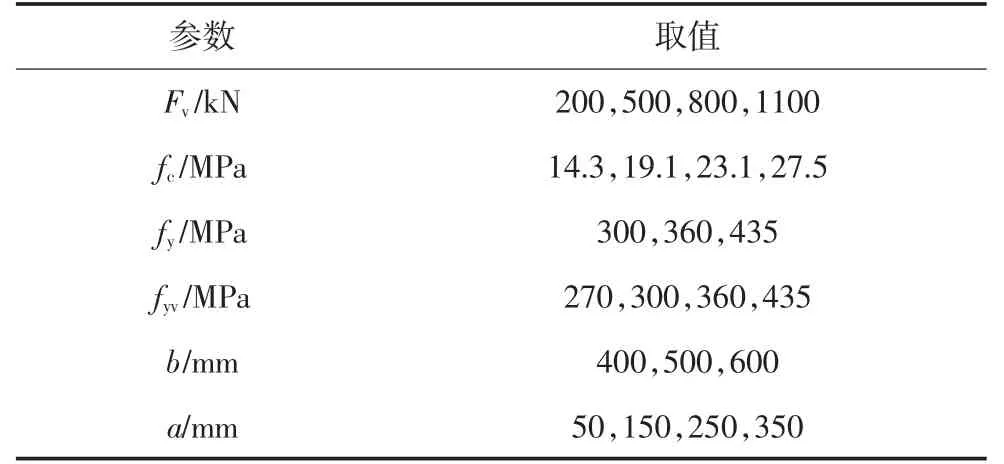
表3 参数取值表Tab.3 Parameter values
为了评估按照规范设计的钢筋混凝土牛腿的抗剪承载力,定义牛腿抗剪承载力安全系数α0:

式中:FSTM为将某牛腿的设计参数代入软化拉压杆模型计算得到的牛腿抗剪承载力;Fv为该牛腿的设计荷载.α0值越大,说明按照规范设计的牛腿抗剪承载力安全余度越高.根据第1.2 小节软化拉压杆的受力机理分析可知,牛腿的抗剪承载力主要由混凝土的抗剪承载力和箍筋的抗剪承载力组成,为了定量分析混凝土和箍筋对抗剪承载力的贡献,定义如下参数:

式中:Fc,STM为软化拉压杆模型中混凝土贡献的抗剪承载力,即保持其他参数不变,将箍筋面积取为0 而得到的承载力;Fh,STM为软化拉压杆模型中箍筋贡献的抗剪承载力,是将总的牛腿抗剪承载力计算值FSTM减去混凝土贡献的部分Fc,STM而得到的.
3.1 混凝土强度
增大混凝土强度,按照规范设计的牛腿高度将减小,纵筋面积和箍筋面积将增大.牛腿承载力系数随着混凝土强度的变化规律如图10(a)所示.当混凝土强度由14.3 MPa 增大到27.5 MPa 时,承载力安全系数α0由1.07 提高至1.40.原因是混凝土承担的剪力将随着混凝土强度增加而显著增大,说明混凝土强度提升和钢筋面积增加对抗剪承载力的贡献大于牛腿高度减小对承载力的降低作用.随着混凝土强度提升,箍筋对牛腿承载力的贡献有降低的趋势,原因是随着混凝土强度增大,牛腿高度将减小,造成牛腿剪跨比增大,使得箍筋对牛腿承载力的影响降低.
3.2 纵筋强度
增大纵筋强度,按照规范设计的牛腿纵筋面积和箍筋面积将减小.牛腿承载力系数随着钢筋强度的变化规律如图10(b)所示.当纵筋强度由300 MPa增大到435 MPa 时,承载力安全系数α0由1.35 降低至1.11.原因是随着纵筋强度增大,牛腿纵筋面积和箍筋面积均减小.纵筋面积减小使得按拉压杆模型平衡条件确定的混凝土压杆面积减小,造成混凝土承担的剪力减小;箍筋面积减小造成箍筋承担的剪力减小.因此,随着纵筋强度的增大,混凝土和箍筋承担的剪力均减小,导致牛腿承载力降低.
3.3 剪切跨度
增大剪切跨度,按照规范设计的牛腿高度将增大;当剪切跨度小于150 mm 时,剪跨比小于0.3,配筋面积保持不变;当剪切跨度由150 mm 增大到350 mm 时,配筋面积将增大.牛腿承载力系数随着剪切跨度的变化规律如图10(c)所示.当剪切跨度由50 mm 增大到150 mm 时,承载力安全系数α0由1.59降低至1.18.原因是箍筋承担的剪力显著减小,说明牛腿高度增加对抗剪承载力的贡献小于箍筋对承载力的降低作用.当剪切跨度由150 mm 增大到350 mm 时,承载力安全系数α0由1.18 提高至1.34.原因是混凝土承担的剪力显著增大,说明牛腿高度和纵筋面积增加对抗剪承载力的贡献大于箍筋对承载力的降低作用.
3.4 箍筋强度
按照规范牛腿箍筋为构造要求.牛腿承载力系数随着箍筋强度的变化规律如图10(d)所示.当箍筋强度由270 MPa 增大到435 MPa 时,承载力安全系数α0由1.21 提高至1.24.原因是箍筋承担的剪力将随着箍筋强度增加而增大,随着箍筋强度提升,混凝土对牛腿承载力的贡献几乎不变.

图10 不同设计参数对牛腿安全度的影响Fig.10 Influence of different design parameters on the safety of corbels
3.5 设计荷载
增大设计荷载,按照规范设计的牛腿高度将增大,纵筋面积和箍筋面积将增大.牛腿承载力系数随着设计荷载的变化规律如图10(e)所示.当设计荷载从200 kN 增大到1 100 kN 时,承载力安全系数α0由1.51 降低至1.15.原因是混凝土承担的剪力将随着设计荷载的增加而显著减小,说明随着设计荷载的增大,牛腿高度和纵筋面积增加对抗剪承载力的贡献降低.随着设计荷载增大,箍筋对牛腿承载力的贡献有升高的趋势,原因是随着设计荷载增大,箍筋面积将增大,使得箍筋对牛腿承载力的贡献提高.
3.6 牛腿宽度
增大牛腿宽度,按照规范设计的牛腿高度将减小,纵筋面积和箍筋面积将增大.牛腿承载力系数随着牛腿宽度的变化规律如图10(f)所示.当牛腿宽度由400 mm 增大到600 mm 时,承载力安全系数α0由1.22 提高至1.36.原因是混凝土承担的剪力将随着牛腿宽度的增大而增加,说明纵筋面积和牛腿宽度的增加对抗剪承载力的贡献大于牛腿高度减小对承载力的降低作用.随着牛腿宽度增大,箍筋对牛腿承载力的贡献有降低的趋势,原因是随着牛腿宽度增大,牛腿高度将减小,造成牛腿剪跨比增大,使得箍筋对牛腿承载力的影响降低.
4 抗剪承载力简化公式
基于参数分析的结果,本节将提出牛腿承载力安全系数α0的计算公式,并将其定义为承载力修正系数α,用于修正我国规范设计公式.
通过参数分析可知,影响承载力安全系数α0的主要参数为混凝土强度fc、纵筋强度fy、设计荷载fv以及剪切跨度a;根据图10(a)(b)和(e),承载力安全系数α0与混凝土强度fc、纵筋强度fy、设计荷载Fv呈线性关系,根据图10(c),承载力安全系数α0与剪切跨度a 呈抛物线关系.为拟合承载力修正系数α的公式,用牛腿高度h 表征设计荷载Fv;为消除量纲对拟合公式的影响,定义以下无量纲参数,fc/f*c、f*y/fy、h*/h、a/a*,其中f*c、f*y、h*、a*为标准模型的设计参数值.基于参数分析的结果假定函数的形式,跟fc/f*c、f*y/fy和h*/h 呈线性关系,跟a/a*呈抛物线关系.采用Origin 多元非线性拟合,可得到承载力修正系数α 的简化公式(4).
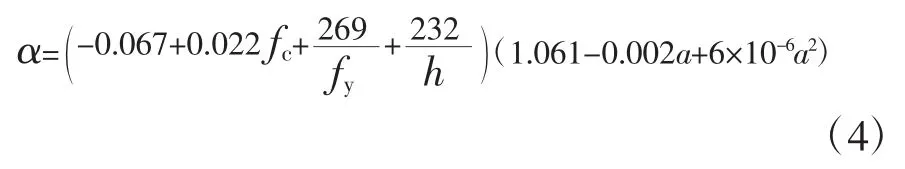
承载力修正系数公式的拟合结果如图11 所示,图中的数据点均来自于第3 节中参数范围内的牛腿试件.图11 中横坐标为公式(4)的计算结果,纵坐标为参数分析的理论计算结果.承载力调整系数理论计算结果与公式(4)计算结果的比值平均值为1.001,变异系数为0.023,说明了拟合的承载力修正系数公式与参数分析的结果吻合较好.

图11 承载力修正系数拟合结果Fig.11 Fitted results of modification factor for shear capacity
将承载力修正系数α 作为我国规范牛腿承载力计算公式的调整系数,由式(4)得到修正后的我国规范牛腿承载力计算公式(5).

为了验证修正后的我国规范牛腿承载力计算公式的准确性,将公式(5)计算结果与文献[3,14-24]中的试验数据做比较.结果如图12 所示,ηm为1.06,说明规范采用调整系数α 后承载力计算结果更加准确.将209 组试验数据按配筋是否满足我国规范要求分为两类,满足规范的有36 组,不满足规范的有173 组.其中满足规范的试件承载力预测结果离散度更小,进一步说明了承载力修正系数α 可为规范牛腿设计提供参考.

图12 承载力修正公式计算结果Fig.12 Calculation results of modified Chinese code formula
5 设计建议
从第3 节的分析中可以看出,我国规范设计牛腿的实际承载力均大于设计荷载,说明规范方法偏于保守.在满足正常使用阶段牛腿不出现斜裂缝(即牛腿尺寸不变)的前提下,可以通过降低构造箍筋的数量来更为准确和经济地满足牛腿抗剪承载力要求.图13 为牛腿抗剪承载力安全系数α0随着实配箍筋数量与设计箍筋数量比值β 的变化规律.在不同的设计参数下,α0随着实配箍筋数量的增加而提高.当实际箍筋面积小于设计箍筋面积的80%时,部分试件出现了α0小于1 的情况,说明此时牛腿实际承载力小于设计承载力.当实际箍筋面积大于设计箍筋面积的80%时,各个设计参数下的试件α0均大于1,说明此时牛腿实际承载力大于设计承载力.因此当实配箍筋数量减少为设计箍筋数量的80%时,牛腿的实际抗剪承载力均能满足设计要求.

图13 箍筋面积对承载力的影响Fig.13 Influence of stirrup area on shear capacity
6 结论
本文采用209 组牛腿受剪试验数据评估了各国规范和国外主要拉压杆牛腿承载力计算模型,然后采用软化拉压杆模型对满足我国规范的牛腿承载力进行分析,得到以下结论:
1)规范拉压杆模型牛腿承载力计算方法偏于保守并且和试验数据对比离散性大.并且规范STM 均不适用于剪跨比极小(≤0.1)的牛腿,但ACI STM 和CSA STM 均未限制压杆角度的最大值;在剪跨比较大时CSA STM 较好地反映了剪跨比对牛腿承载力的影响.ACI STM 和CSA STM 不适用于高强混凝土牛腿,而EC2 STM 考虑到了混凝土抗压强度对牛腿受剪承载力的影响.
2)满足我国规范的牛腿承载力随着混凝土强度fc的增大而提高,随着纵筋强度fy、牛腿高度h 的增大而减小.当剪跨比小于0.3 时,增大剪切跨度满足我国规范的牛腿承载力降低;当剪跨比大于0.3 时,增大剪切跨度满足我国规范的牛腿承载力提高.牛腿宽度和箍筋强度对满足我国规范的牛腿承载力影响比较小.
3)软化拉压杆模型能准确预测牛腿承载力并且能反映混凝土强度、剪跨比、纵筋配筋率、箍筋配筋率各个关键参数对牛腿受剪承载力的影响规律.基于软化拉压杆模型提出了承载力修正系数α 的简化计算公式.简化公式的计算值与试验值吻合良好,可为工程实际提供参考.
4)我国规范设计牛腿的实际承载力均大于设计荷载,当实配箍筋数量减少为设计箍筋数量的80%时,牛腿的实际抗剪承载力均能满足设计要求.

