斜拉桥多索-浅拱-弹性约束模型及面内自由振动
苏潇阳,康厚军,皮梓豪,丛云跃
(湖南大学 土木工程学院,湖南 长沙 410082)
斜拉桥由于受力性能好、抗震性能强、造型优美 及优越的跨越能力在大跨度桥梁中占有十分重要的地位.但由于斜拉桥跨度的不断增大以及新材料的不断应用,结构也变得更轻更柔,其动力学问题也就更为突出.因此,国内外学者对斜拉桥的动力学特性进行了大量研究.Gattulli 等[1]通过经典变分公式,建立了斜拉桥索-梁结构横向动力学运动控制方程,并对其特征值问题进行了参数分析.本课题组[2-5]采用传递矩阵法对斜拉梁、双索梁结构的面内振动问题进行了详细的分析.通过考虑斜拉桥中桥塔的振动,提出了多梁离散弹簧动力学整体模型,并对斜拉桥的整体竖弯刚度进行了评估,探究了拉索对斜拉桥竖向振动频率的影响.Cao 等[6]提出了由四根拉索和桥面梁组成的斜拉桥模型,并对该模型的线性特征值问题进行了深入的研究,该模型将桥面塔视为刚性,忽略了桥塔的振动.然而,在实际工程中,大跨度斜拉桥的桥面梁一般具有一定的预拱度以满足排水的需要,上述研究都没有考虑斜拉桥桥面梁的初始构型,这对理解斜拉桥的动力学行为难免有偏差.鉴于此,考虑桥面梁的初始构型,Kang 等[7]建立了斜拉桥的双索-浅拱动力学模型,对端部轴向简谐激励下的1 ∶1 ∶1 内共振动力学问题进行了研究.丛云跃等[8]基于索和浅拱的经典动力学方程,对双索浅拱的面内自由振动进行了研究.
以上研究均将斜拉桥的边界条件模拟为简支,实际上在基础变形以及由于基础变形所引起的附加惯性力的影响下,这可能会导致计算出的模型固有频率显著降低[9],尤其是低阶的频率.所以建立相应的弹性支承模型更符合实际工程情况.因此,国内外学者对弹性约束下各种模型的动力学特性进行了研究.易壮鹏等[10]研究了两端弹性约束浅拱的自由振动特性和非线性动力特性.Ding 等[11]建立了带有非线性隔振的微曲梁的非线性动力学模型,研究了具有弹性边界的弯曲梁动力学问题,并推导了具有弹性边界的弯曲梁的模态函数和频率公式.
论文在上述研究的基础上,为建立更为精细的斜拉桥动力学模型,考虑斜拉桥桥面板的初始构型以及支座刚度的影响,建立两端竖向弹性支承的多索-浅拱动力学模型,并对该模型进行参数分析.论文模型相比于其他模型(例如索梁模型)更接近斜拉桥的真实状态,可以对斜拉桥的面内特征值问题进行分析,从而更准确地揭示斜拉桥的动力学特性.另外,基于该模型可以对斜拉桥的非线性振动进行研究,揭示斜拉索的大幅振动机理,为实际工程提供参考.
1 两端弹性约束多索-浅拱模型
考虑支座处基础变形的影响,将模型两端支座简化为竖向弹性支承,论文暂不考虑支座处转动弹性支承[12].图1 为考虑斜拉桥初始构型之后,两端竖向弹性约束的多索-浅拱模型,分别建立坐标系soy和xjojyj(j=1,2,…,n)描述浅拱和索的振动,根据索的数量将浅拱分为i 段,i=1,2,…,n+1.在能体现问题本质的前提下做出如下假设:
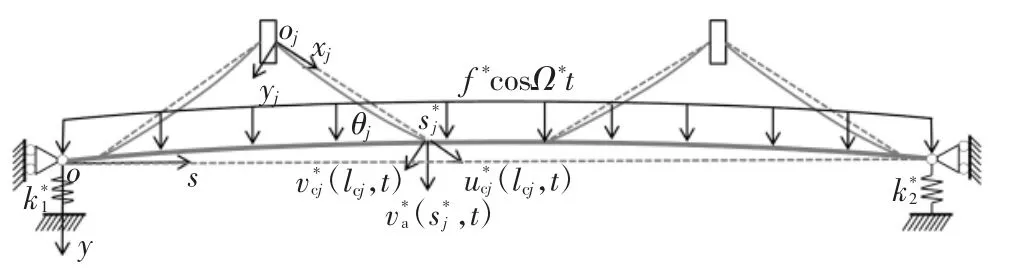
图1 两端弹性约束多索-浅拱模型Fig.1 The multi-cable-stayed shallow-arch model with elastic constraints at both ends
1)桥塔为刚性塔,对索以及浅拱产生的影响忽略不计;
2)由中线的Lagrangian 应变来描述拉索的轴向应变,忽略索的扭转、弯曲、剪切刚度及轴向惯性力的影响;
3)忽略浅拱轴向、扭转、剪切变形的影响.
4)考虑浅拱的几何非线性影响,浅拱的静态构型:y0(s)=(f*/la)sin(πs*/la).其中f*为浅拱的矢高.
5)斜拉索的静态构型:
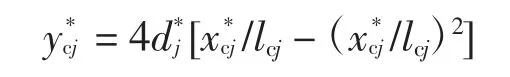
通过Hamilton 原理得到每根索和每段浅拱的面内振动微分方程[13]:
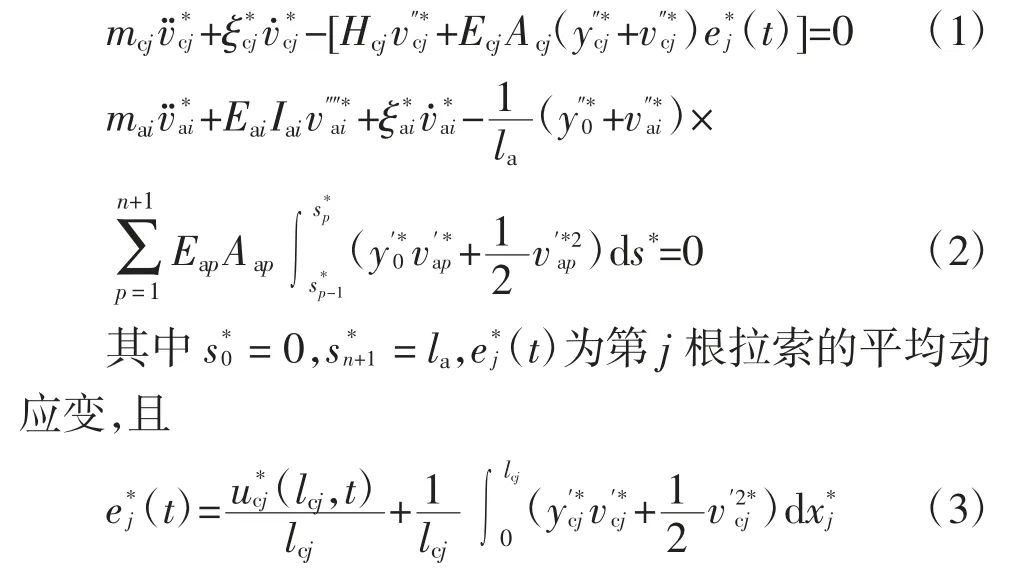
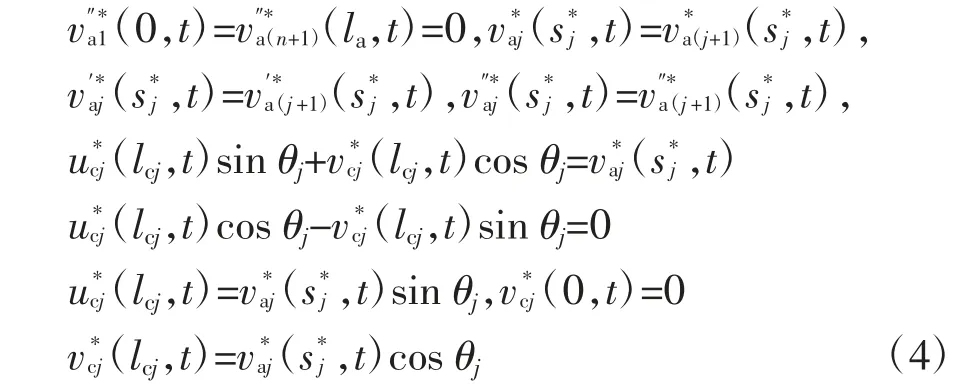
式中:θj表示拉索的倾角,即拉索与水平方向的夹角.拱进行分段以后,节点两侧应满足如下力学协调关系:
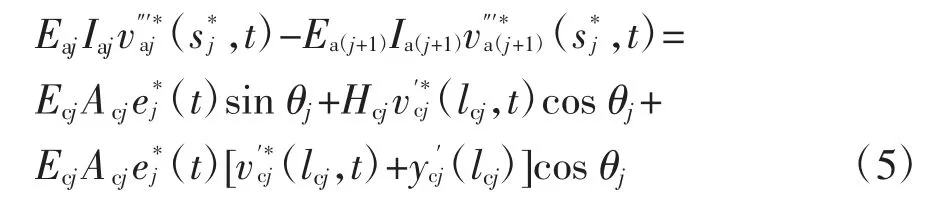
由Hamilton 原理还可以得到力学边界条件:
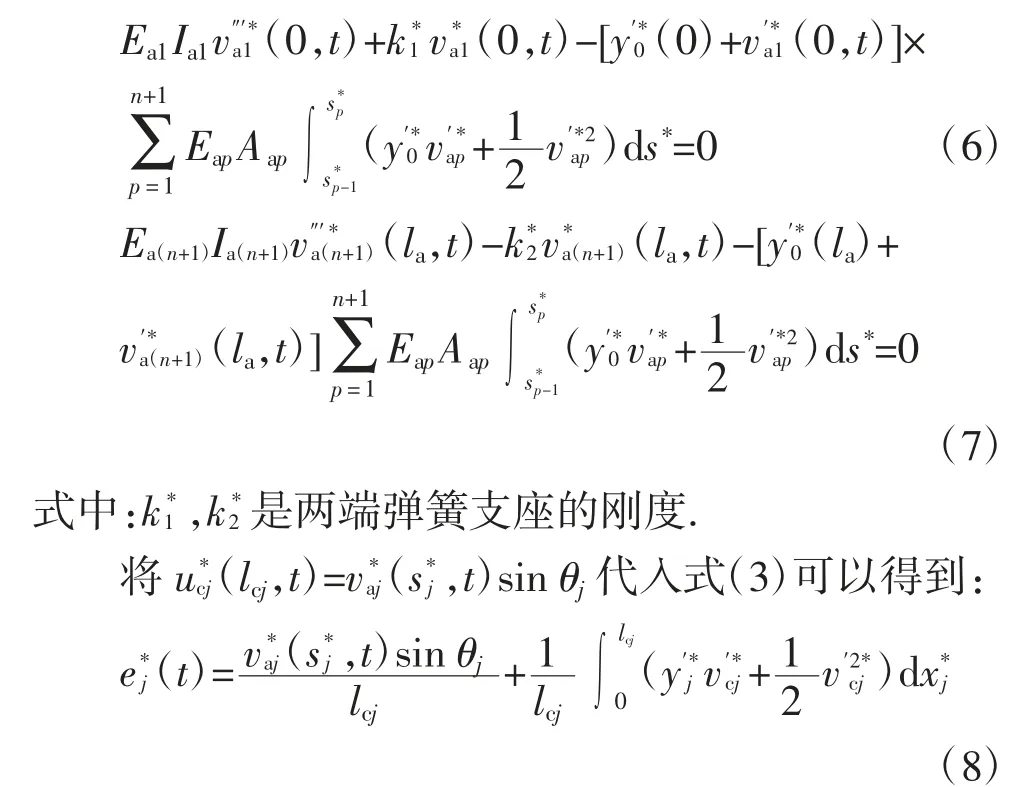
2 面内特征值问题
首先引入以下无量纲量:

为了求解模型的面内特征值问题,忽略索和浅拱振动方程中的非线性项和阻尼项,从而得到索和浅拱面内自由振动方程的线性形式:
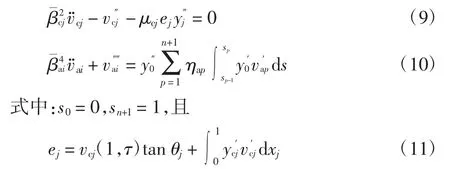
同理可以得到式(5)-(7)的无量纲线性形式:
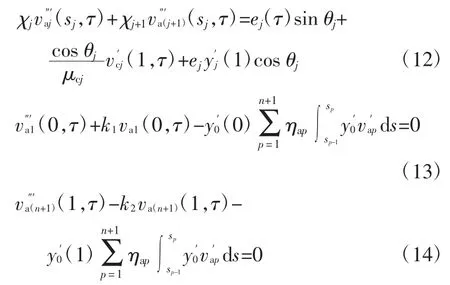
为计算方便,论文以竖向弹性约束双索-浅拱模型为例进行求解.假定模型为对称结构,由于两根索和各段浅拱的物理参数完全相同,为书写方便,接下来的表达式中去掉了各物理参数的下标i 和j.根据分离变量法,索和浅拱的位移可以表示为:
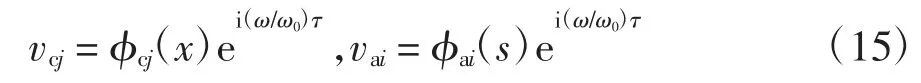
式中:j=1,2,且i=1,2,3.将式(15)分别代入式(9)和(10),可以得到:
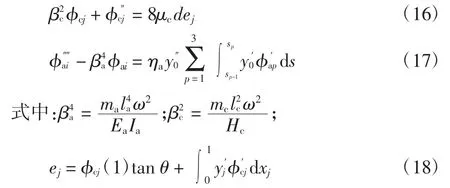
将式(15)代入式(4),(12)-(14)可以得到:
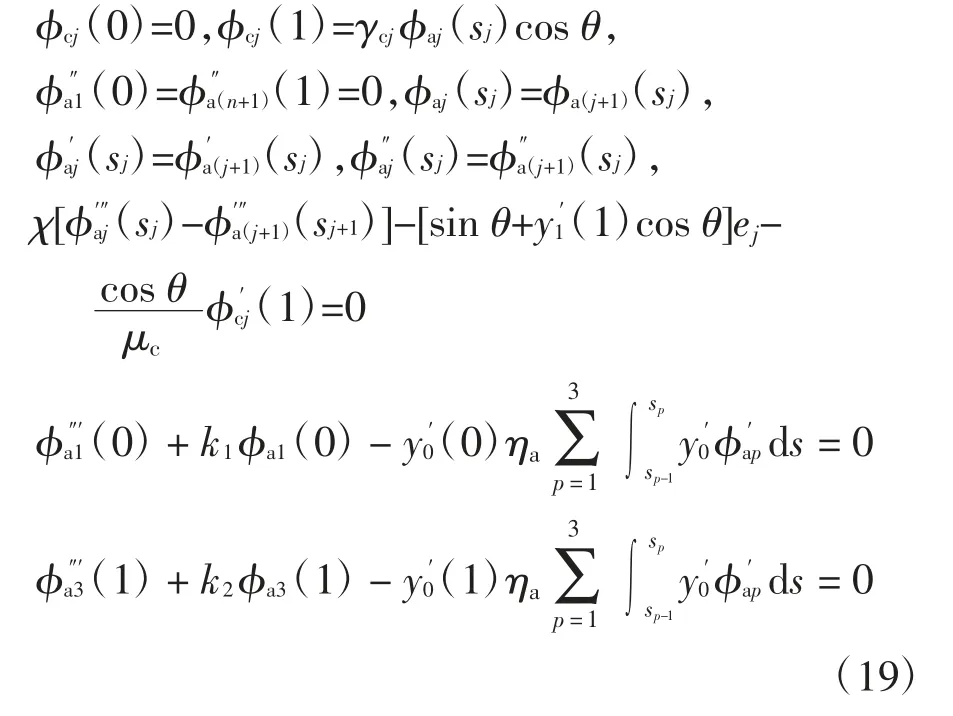
方程(16)的通解为:
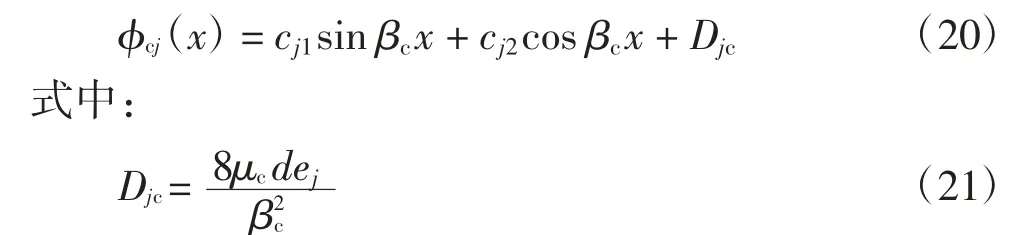
由假设(4)和(5),浅拱和索的无量纲初始静态构型为:

将式(20)和(23)代入式(18)并与式(21)联立求解,可以得到:
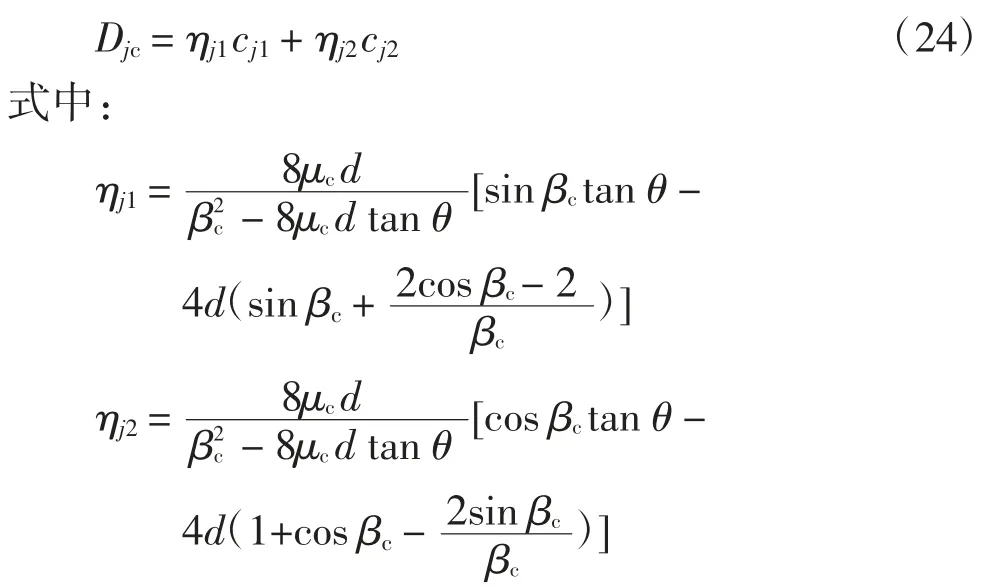
方程(17)的通解为:
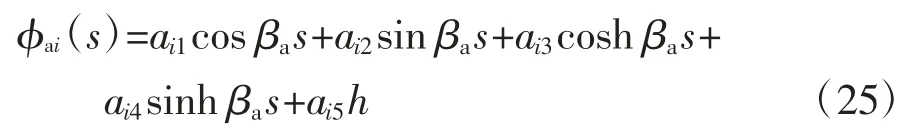
式中:h 为方程的特解,与浅拱的初始构型表达式(22)有关,这里h=sin πs.
式(25)代入方程(17)可以得到3 个式子,连同式(19)一共19 个式子,将他们写成矩阵形式可以得到系统的特征方程如下式(26)所示,当其系数矩阵行列式的值为0 时方程组有非平凡解.

式 中:{X}={cj1,cj2,ai1,ai2,ai3,ai4,ai5}T.特征方程(26)的系数矩阵行列式是面内自振频率ω 的函数,通过求解特征方程可以得到各阶频率值,进而求得各阶振型.
3 数值分析
3.1 模态分析
选取以下物理参数进行简要数值分析:浅拱弹性模量34.5 GPa,跨径300 m,截面惯性矩9.8 m4,单位长度质量4.4 × 104kg/m;斜拉索弹性模量210 GPa,长度115.5 m,单位长度质量10.4 kg/m,横截面积6.3×10-3m2,初始索力1 MN,拉索倾角30°.实际工程中支座的竖向刚度大概有7 个数量级,因此选取两端弹性支座的无量纲刚度为k1=k2=1 000.对应的实际刚度为1.25×107N/m.
为验证论文方法的正确性,利用有限元分析软件ANSYS15.0 建立了相应的有限元模型.斜拉索采用Link1 单元模拟,浅拱采用Beam3 单元模拟,弹性支承采用Combine14 单元模拟.表1 和图2 列出了根据论文方法和有限元模拟得到的结构前八阶频率和前五阶模态.可以看到,论文方法计算得到的结果和有限元模拟得到的结果吻合非常好,虽然第五阶频率的相对误差稍微有点大,但其绝对误差只有0.055 6(1.098 1~1.042 5).另外,仔细观察第五阶模态可以发现,索在有限元中只有拖动效应,而没有自身的振动,论文算法中体现出了索的自身振动和拖动效应,从而使索力加大,进而提高了结构的整体刚度,因此导致第五阶频率误差较大.
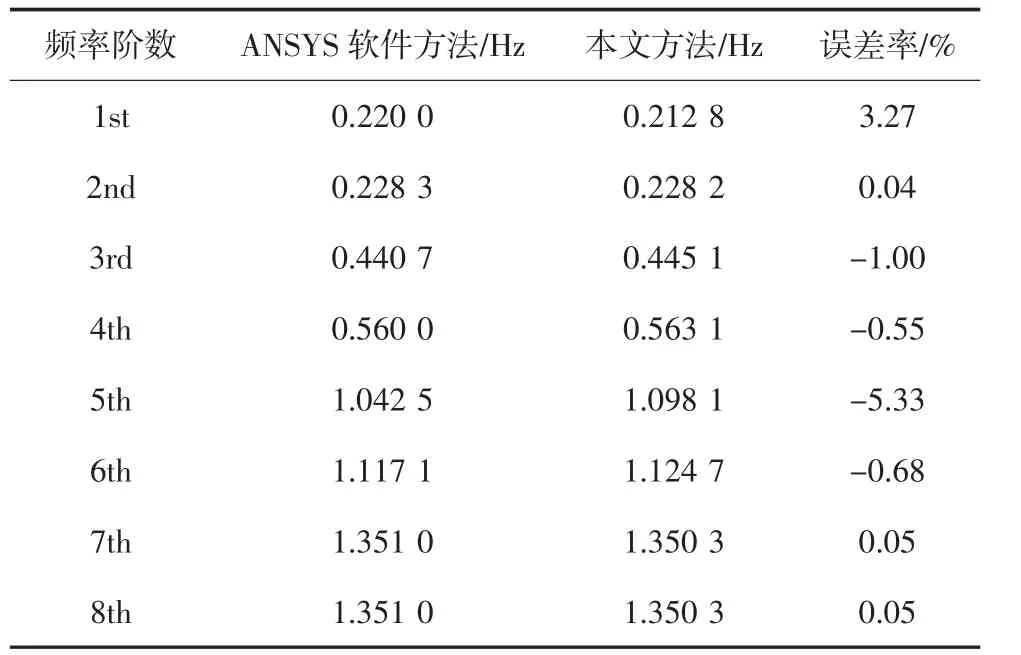
表1 弹性约束双索-浅拱前八阶频率Tab.1 The first eight frequencies of double-cable-stayed shallow-arch model with elastic constraints at both ends
3.2 参数分析
为研究基于该模型的斜拉桥更多动力学特性,采用论文中的计算方法对相关重要参数进行了分析.
图3 给出了结构的前五阶频率值随支座刚度的变化曲线,这里假定两侧支座刚度相等,即k1=k2=k,且同时变化.从图中可以看出随着支座刚度的增加,各阶频率曲线有上升的趋势.根据等效频率公式,刚度越大,结构自振频率越大.另外,从图2 和图3 中可以看出在支座位移比较大的模态中,例如第二、第四和第五阶,频率随支座刚度的变化比较明显;而在支座位移比较小的模态中,例如第一和第三阶,频率随支座刚度的变化不明显.这是因为,支座位移大的模态中,弹性支承对结构模态的影响比较大,结构对支座刚度的变化比较敏感;在支座位移较小的模态中,结构对支座刚度的变化不敏感.
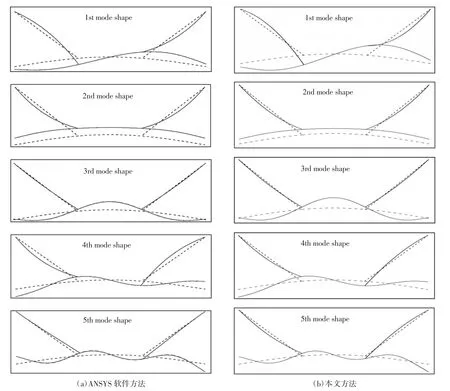
图2 弹性约束双索-浅拱前五阶模态Fig.2 The first five mode shapes of double-cable-stayed shallow-arch model with elastic constraints at both ends
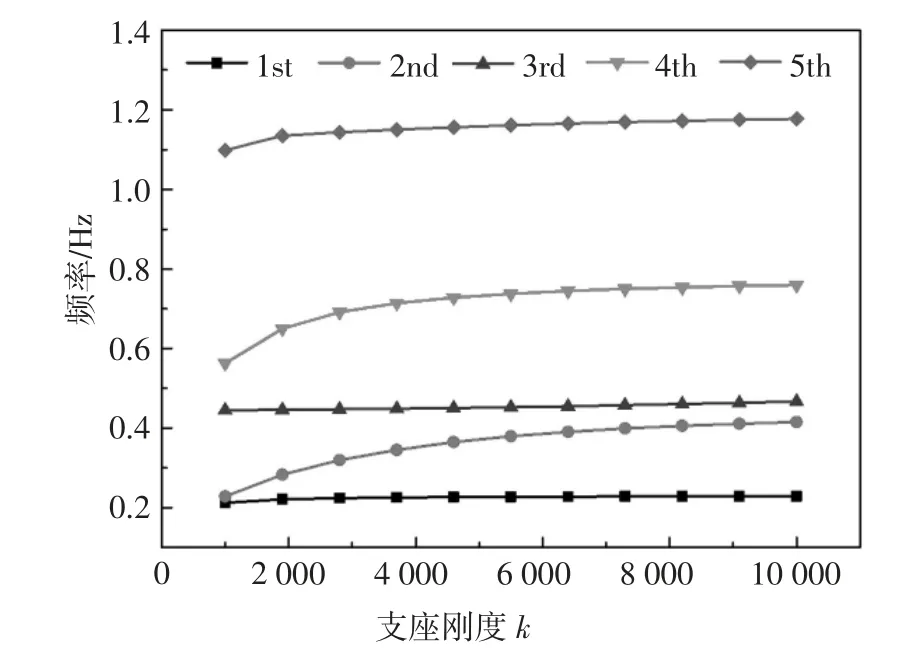
图3 支座刚度对模型前五阶频率的影响曲线Fig.3 Effect of the support stiffness on the first five frequencies
图4 给出了k=1 000 和k=10 000 下模型的前五阶频率随浅拱矢跨比的变化曲线.从图中可以看出:在一定矢跨比范围内,某阶频率会随着矢跨比的增加而变大,随着矢跨比的继续增加,该阶频率将不再改变.论文称该影响范围为矢跨比对频率的影响域,随着支座弹簧刚度的变化,这个影响域也会随之发生变化.
另外,图4(a)中的前两阶频率,图4(b)中的前三阶频率之间分别出现了频率曲线相互靠近而又分离的现象,即veering 现象,这与文献[8]中观察到的现象一致.然而,各阶频率对支座弹簧刚度的敏感程度不同,如图3 所示,第一、三阶频率随支座刚度的增加变化较小,因此在图4(a)中,veering 现象发生在前两阶频率之间,而在图4(b)中,veering 现象发生在前三阶频率之间.仔细观察图4(a)可以发现,当f=0.022 5 时,ω2≈ω1;当f=0.018 3 时,ω3≈2ω2.这表明模型各阶频率之间存在多种内共振关系,此时相邻阶模态之间会发生能量传递和模态互换,并导致索的大幅振动,工程中应注意设计参数以避免此现象的发生.
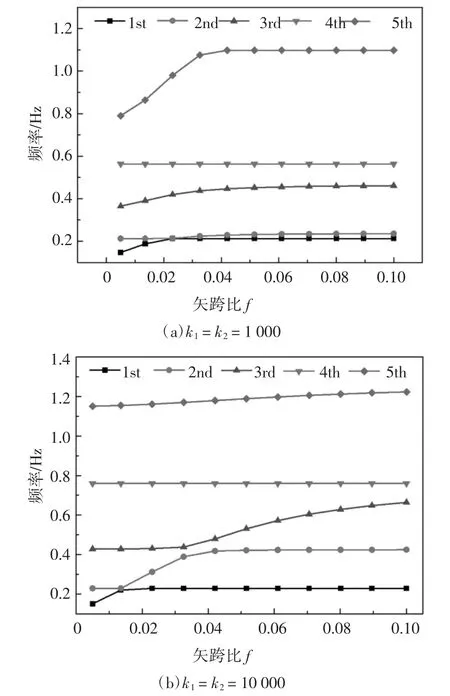
图4 浅拱矢跨比对模型前五阶频率的影响曲线Fig.4 Effect of the rise-to-span ratio of the shallow arch on the first five frequencies
图5 给出了拉索垂度对模型的前五阶频率的影响曲线.从图中可以看出前四阶模态频率随着拉索垂度的增加而缓慢减小,这是因为前四阶模态中拉索的振动主要由浅拱的拖动造成,随着拉索垂度的增加,拉索等效刚度减小,整体结构刚度也减小,从而频率减小.第五阶频率随着拉索垂度的增加先减小后增加,这是因为随着垂度的进一步增加,索与水平方向的夹角减小,索力的水平分量变大,从而导致浅拱的几何刚度增大,结构的频率增大.第五阶模态拉索自身振动幅度较大,因此拉索垂度对模型频率的影响也更加明显.
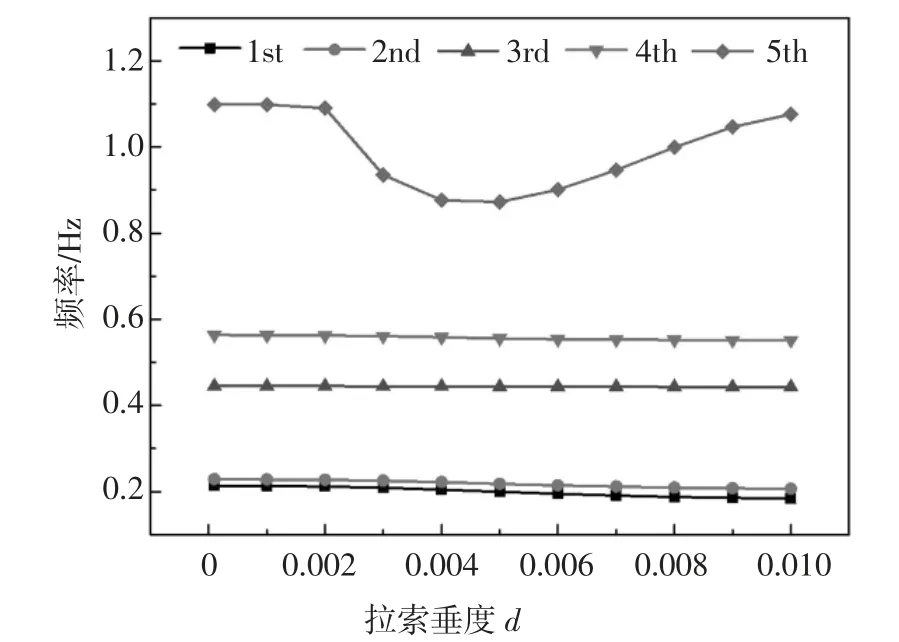
图5 k=1 000 时拉索垂度对模型的前五阶频率的影响曲线Fig.5 Effect of the sag of the cable on the first five frequencies when k=1 000
图6 给出了拉索倾角对模型前五阶频率的影响曲线.从图中可以看出,前两阶频率随着拉索倾角的增加先缓慢增加,再缓慢下降,但总体来说变化幅度很小.当拉索倾角较小时,三、四、五阶频率随拉索倾角的增加变化不大,当拉索倾角继续增加到一定值时,频率会显著下降.这是因为随着倾角的增大,拉索两端锚固点水平距离不变,斜拉索变长,质量也随之增加,因此频率变小[14,15].另外,当拉索倾角增加到1.2 左右时,第四阶和第五阶频率很接近,这是因为此时第四阶和第五阶模态都是索单独振动的局部模态,第四阶是反对称模态,第五阶是正对称模态;而当拉索倾角增加到1.3 左右时,局部模态变为第三阶和第四阶,因此第三阶和第四阶的频率曲线发生了重合.
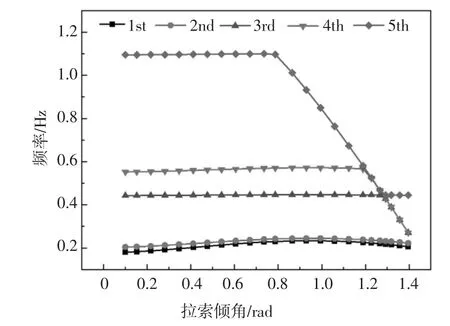
图6 k=1 000 时拉索倾角对模型前五阶频率的影响曲线Fig.6 Effect of the incline degree of cable on the first five frequencies when k=1 000
4 结论
论文考虑斜拉桥的初始构型和更合理的支承条件,建立了竖向弹性约束下的多索-浅拱动力学模型.基于索和浅拱的经典动力学方程,将浅拱在索-拱耦合处分段,推导了竖向弹性约束多索-浅拱的面内自由振动理论.以竖向弹性约束双索-浅拱模型为例,对其面内特征值问题进行了求解,通过与有限元模拟得到的结果进行对比,表明论文方法和模型的正确性.最后,对模型的动力学特性进行了详细的参数化分析并由此得出如下结论:
1)随着弹性支座刚度的增加,结构的各阶频率增加,在支座位移大的模态中,频率对支座刚度变化更为敏感.支座刚度会影响系统内共振的发生从而影响系统的动力学行为,将两端边界条件视为弹性约束更合理.
2)增加浅拱矢跨比会使得结构的某阶频率明显增加,从而改变结构的内共振关系,在斜拉桥动力特性分析中应当考虑桥面梁初始构型所造成的影响.
3)改变浅拱矢跨比和拉索倾角会产生veering 现象.支座刚度的变化会影响这一现象的出现,刚度越大该现象越明显.
4)拉索垂度对低阶频率影响不明显,对高阶频率的影响较为明显.拉索倾角对局部模态影响较大,因此在进行拉索设计时应该设计合适的倾角,避免局部模态出现在低阶模态而产生内共振.

