基于不同归一化参数的单自由度体系残余位移比离散性研究
胡进军,刘巴黎
(1.中国地震局 工程力学研究所,黑龙江 哈尔滨 150080;2.中国地震局地震工程与工程振动重点实验室,黑龙江哈尔滨 150080)
结构在强震作用下进入非线性阶段会产生不可恢复的残余位移[1],结构残余位移是抗震性能评估和地震损失评估的重要参数[2-5].FEMA P-58[6]将残余位移作为决定结构震后修复或拆除的重要指标.《建筑抗震韧性评价标准》(GB/T 38591—2020)[7]中建筑的抗震韧性由弹塑性时程分析的层残余变形结合其限值确定,并给出了部分结构形式层残余位移角的限值.
结构自身弹塑性特征的不同会引起地震响应较大的离散性,使得强震下结构性态难以准确预测[8].Kawashima 等[9]对双线性单自由度(SDOF)体系的残余位移进行研究,认为屈服后刚度对残余位移谱离散性影响较大,场地条件、延性系数和自振周期对残余位移谱离散性影响较小.Ruiz-Garcia 和Miranda[10]对SDOF 体系采用弹性谱位移归一化的残余位移比谱进行了系统研究,结果表明强度折减系数对残余位移比谱离散性影响较小,自振周期对残余位移比谱离散性影响较大.胡晓斌和贺慧高[11]采用不同的参数对残余位移进行归一化,对双线性SDOF 体系残余位移离散性进行了研究,结果表明自振周期与屈服后刚度对残余位移离散性有影响,强度折减系数对残余位移比谱离散性影响较小.Harikrishnan 和Gupta[12]采用弹塑性谱位移和弹性谱位移对残余位移进行归一化,对理想弹塑性(EPP)SDOF 体系残余位移比离散性进行了研究,认为延性系数和自振周期对残余位移比离散性有一定的影响,地震动持时对残余位移比离散性影响很小.Harikrishnan 和Gupta[13]对SDOF 体系等强度残余位移比谱进行了进一步研究,结果表明强度折减系数和自振周期对残余位移比离散性有一定的影响.
综上所述,结构弹塑性特征参数(屈服后刚度、延性系数和强度折减系数等)和地震动的随机性对结构残余位移离散性影响的诸多结论不一致.总体而言,与地震作用下结构最大位移响应的离散性相比,结构残余位移响应离散性更大[10].弹塑性特征以及地震动的复杂性和随机性所导致的结构残余位移响应的较大离散性,不仅使得结构残余位移难以准确预测和评估,也成为结构抗震性态评估以及基于性能的抗震设计发展的困难.本文旨在对残余位移的离散性进行系统的研究,从减小结构残余位移比离散性的角度,分析了不同归一化参数对等延性和等强度残余位移比谱离散性的影响,并给出了残余位移比谱离散性较小的归一化参数,同时构建了等延性和等强度残余位移比变异系数谱的拟合公式,为准确预测和评估结构残余位移,实现精细化的抗震设计和评估提供参考.
1 数据来源
本文所选地震动来源于美国太平洋地震工程研究中心(PEER NGA-West2)强震数据库,挑选原则[14]如下:1)矩震级大于5.7;2)地震动峰值加速度(PGA)大于40 cm/s2;3)不包含脉冲型地震动.据此,本文挑选了全球范围内的280 条地震动记录,依据NEHRP[15]规范的场地划分标准分为四类,AB 类(A类和B 类合为一类)、C 类、D 类及E 类,每类场地选取了70 条地震动记录.地震动的震级-断层距分布如图1 所示.
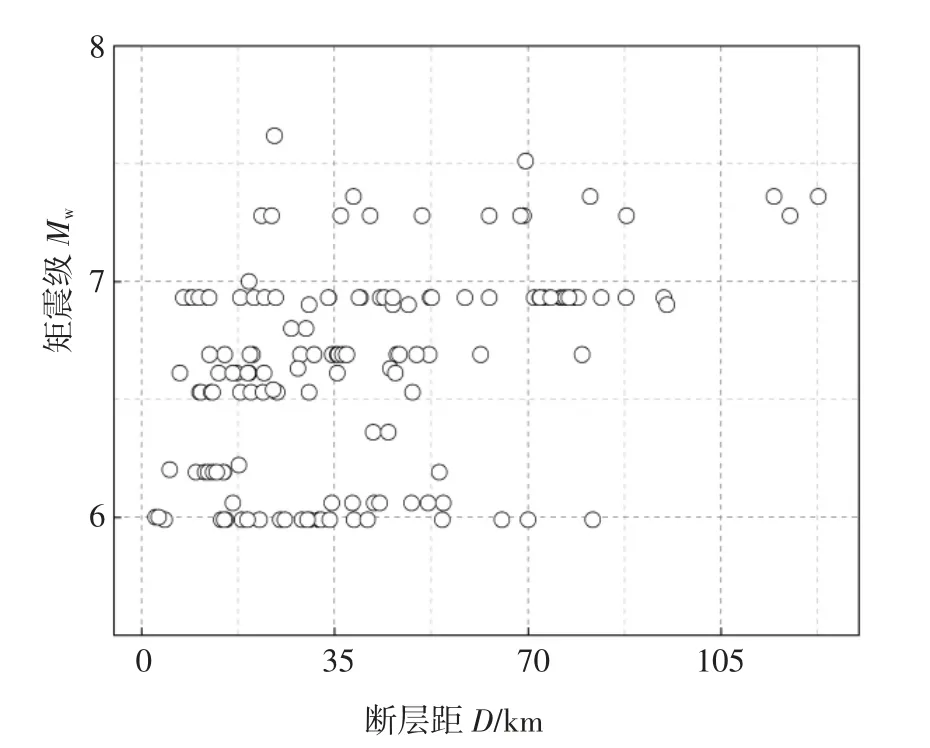
图1 地震动的震级-断层距分布图Fig.1 Magnitude-distance distribution of ground motions
2 残余位移比的定义
研究结构震后残余位移ur时,国内外学者通常将ur进行归一化得到无量纲的残余位移,即残余位移比Cr.常用的归一化参数包括屈服位移uy、最大可能残余位移ur,m、弹塑性谱位移sdi以及弹性谱位移sde.
uy是最早被采用的归一化参数,Mahin 和Bertero[16]通过对EPP 模型的SDOF 体系等延性弹塑性谱进行研究,并且采用屈服位移对残余位移归一化,研究表明结构残余位移可能超过最大弹塑性位移的40%.胡晓斌和贺慧高[11]与Farrow 和Kurama[17-18]也采用屈服位移对残余位移进行归一化研究.
ur,m即结构从最大位移点卸载后剩余的不可恢复的变形.Macrae 和Kawashima[19]采用最大可能残余位移对残余位移进行归一化,首次对双线性SDOF性体系的残余位移进行了系统详细的研究.Kawashima 等[9]采用最大可能残余位移对残余位移进行归一化,进一步研究了屈服后刚度、延性系数、震级、震中距及场地类别对双线性SDOF 体系残余位移比谱的影响.
sdi(Borzi 等[20];Christopoulos 等[21];Harikrishnan和Gupta[12-13])以及sde(Ruiz-Garcia 和Miranda[10];Ji等[22])为最常用的归一化参数.本文分别采用sdi和sde对残余位移进行归一化,定义结构残余位移比Cr.相关参数如图2 所示.
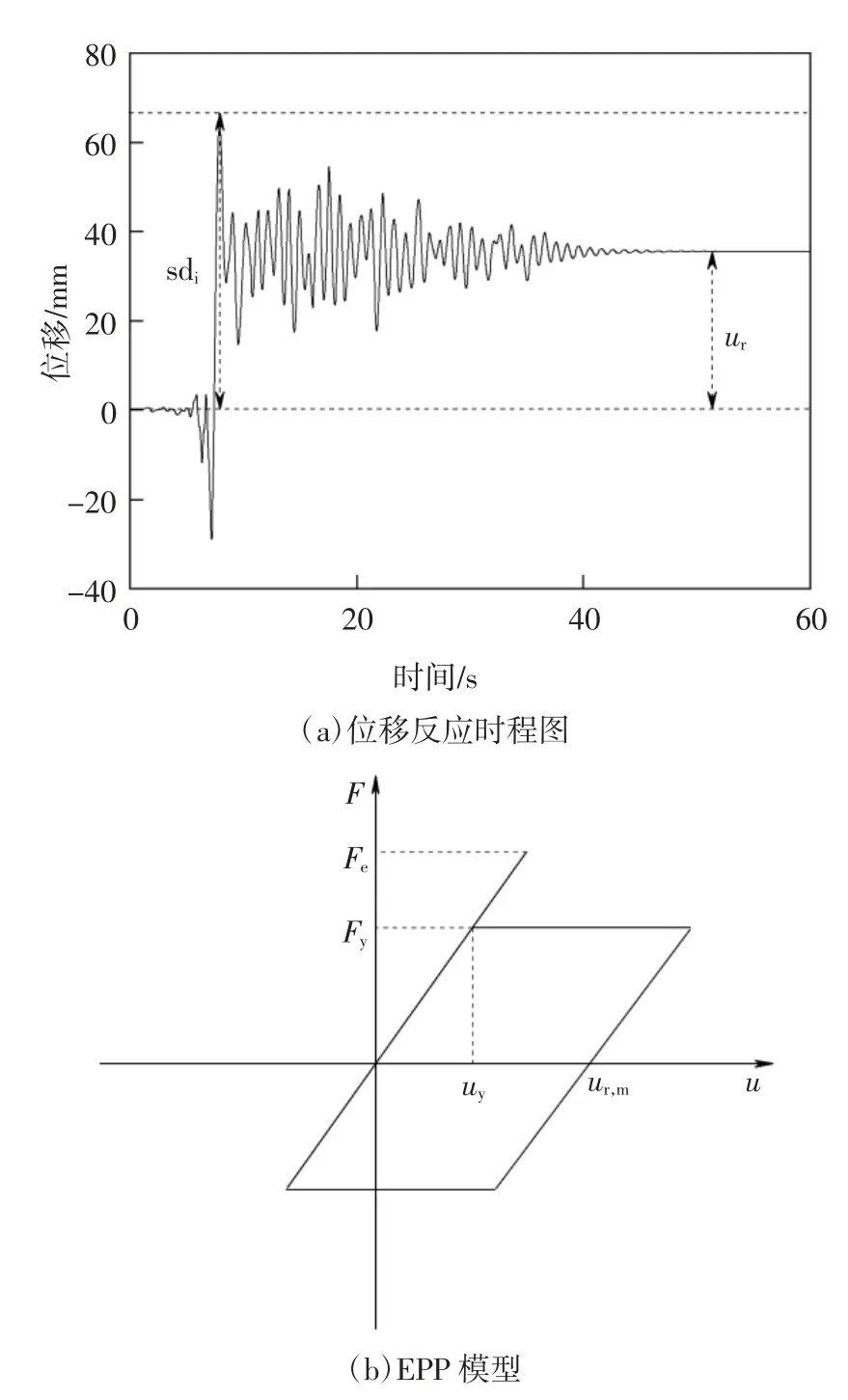
图2 SDOF 体系位移反应Fig.2 Displacements response of SDOF system
3 残余位移与归一化参数相关性分析
本文针对EPP 模型SDOF 体系进行非线性时程分析,采用Newmark-β 法求解运动方程.积分采用文献[23]建议的步长,即:地震动记录采样时间间隔,自振周期的1/25 以及0.01 s 三者的最小值.从已有的文献[10,12,13]可以看出,自振周期大于3 s 时,残余位移比均值谱及变异系数谱谱值趋于不变.因此本文体系自振周期T 取为0.1~3 s,周期间隔为0.1 s.分别计算延性系数μ 为2、3、4、5 和6 时的ur与sdi和sde,以及强度折减系数α 为2、3、4、5 和6 时的ur与sdi和sde.采用Person 相关系数来反映ur与归一化参数相关性的强弱.Person 相关系数的表达式如下所示:
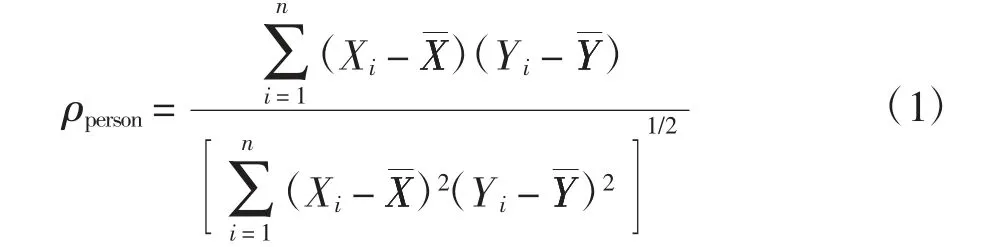
图3 给出了μ 为2、3、4、5 和6 时的ur与sdi和sde的相关系数.图4 给出了α 为2、3、4、5 和6 时的ur与sdi和sde的相关系数.可以看出:
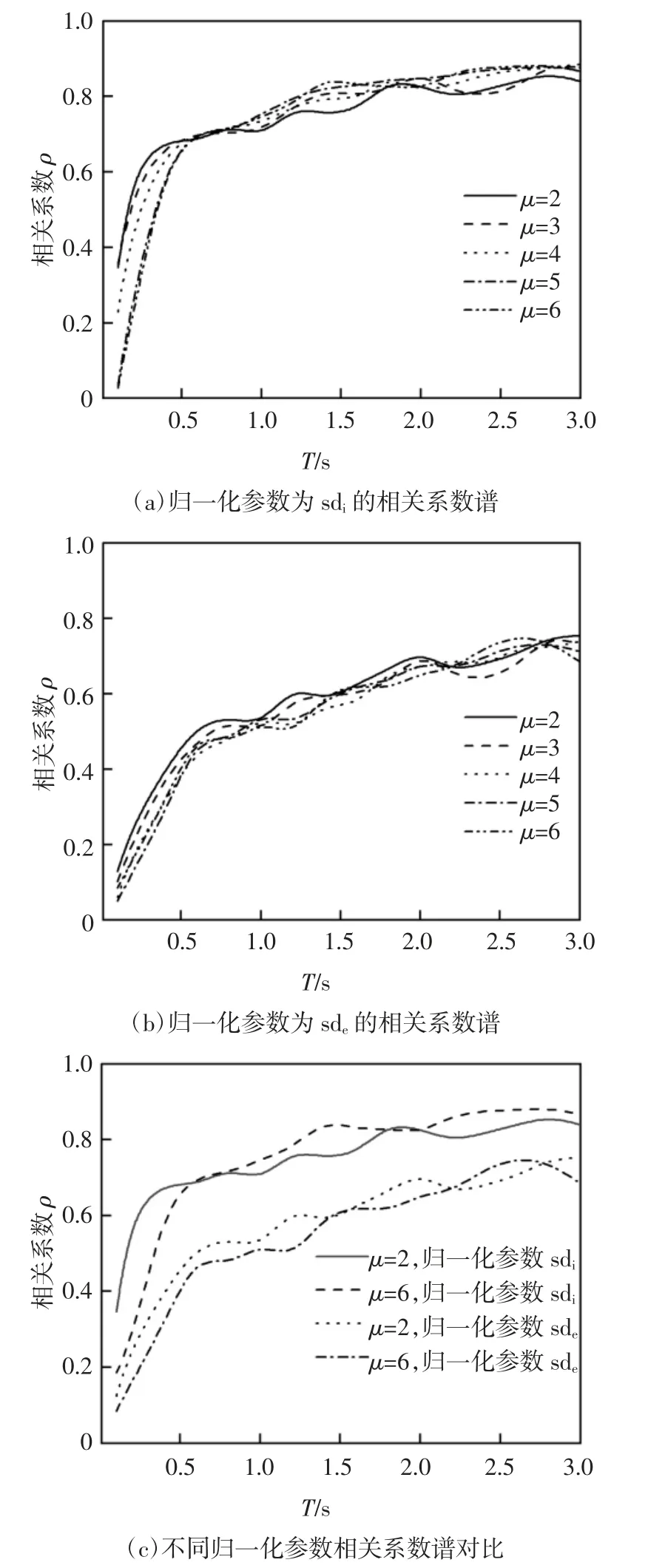
图3 不同归一化参数对应的等延性相关系数谱Fig.3 Correlation coefficient of constant-ductility spectra for different normalized parameters
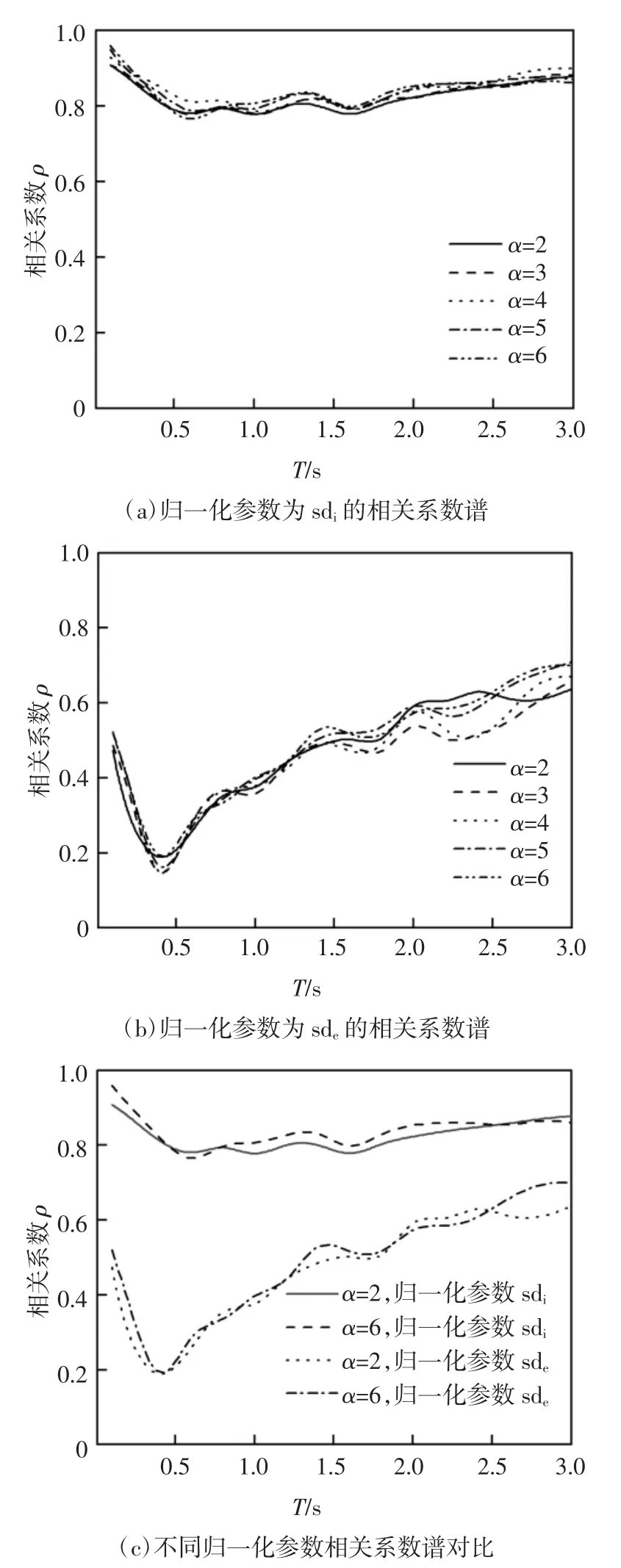
图4 不同归一化参数对应的等强度相关系数谱Fig.4 Correlation coefficient of constant-strength spectra for different normalized parameters
周期小于0.5 s 时,不同μ 的残余位移与归一化参数(sdi和sde)的相关系数随周期增大而增幅较大.周期大于0.5 s 时,不同μ 的残余位移与归一化参数的相关系数随周期增大而增幅较小.
周期小于0.5 s 时,不同α 的残余位移与归一化参数的相关系数随周期增大而减小;周期大于0.5 s时,不同α 的残余位移与归一化参数的相关系数随周期增大而增大;存在临界周期值(0.5 s),大于或小于临界周期值时,不同α 的残余位移与归一化参数之间的相关性趋势发生很大变化,这一点与文献[24]的结论一致.
总体而言,残余位移与归一化参数的相关系数受弹塑性特征参数(μ 和α)的影响较小.残余位移与sdi的相关性较大,与sde的相关性较小.这是因为sdi包含自振周期、阻尼以及反映结构弹塑性特征的参数(延性系数)等信息,而sde中没有包含反映结构弹塑性特征的参数信息.
4 残余位移比谱离散性分析
地震动本身具有极强的随机性,不同的地震动计算结果差距可能高达数倍[25],结构弹塑性特征也会引起地震响应较大的离散性[8],相关研究中各因素对残余位移离散性影响的结论也不一致.本文采用变异系数(COV)来描述和评价残余位移比的离散性,研究延性系数、强度折减系数和场地类别对残余位移比离散性的影响.
4.1 场地条件的影响
按照场地分类AB、C、D 和E 类,计算μ 为2 的各类场地不同归一化参数的等延性残余位移比COV谱,结果如图5(a)和(b)所示.α 为2 的各类场地不同归一化参数的等强度残余位移比COV 谱,结果如图5(c)和(d)所示.可以看出:四类场地等延性和等强度残余位移比COV 谱差距较小,说明结构残余位移的离散性受场地类别的影响较小;结构自振周期小于0.5 s 时,等延性和等强度残余位移比COV 谱随着周期增大而减小;结构自振周期大于0.5 s 时,等延性和等强度残余位移比COV 谱趋于不变,即周期大于0.5 s 时等延性和等强度残余位移比COV 谱对周期变化不敏感.
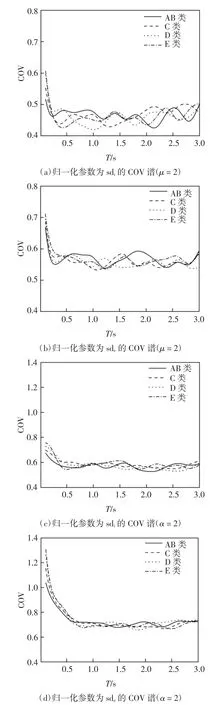
图5 四类场地残余位移比COV 谱Fig.5 COV spectra of residual displacement ratios from different site classes
4.2 延性系数的影响
延性系数μ 为结构最大位移和屈服位移之比.分别取μ 为2、3、4、5 和6,计算四类场地平均等延性残余位移比COV 谱,结果如图6 所示.可以看出:等延性残余位移比COV 谱分别随延性系数的增大而增大.等延性残余位移比离散性受归一化参数的影响较为显著,与sde作为归一化参数的残余位移比COV 相比,sdi作为归一化参数的等延性残余位移比COV 更小.这是因为残余位移与sdi的相关性较大,与sde的相关性较小,选择与残余位移相关性较大的参数(sdi)对其归一化后得到的等延性残余位移比COV 更小.结构自振周期小于0.5 s 时,等延性残余位移比COV 随着周期增大而减小;结构自振周期大于0.5 s 时,等延性残余位移比COV 趋于不变,即周期大于0.5 s 时等延性残余位移比COV 谱对周期变化不敏感.
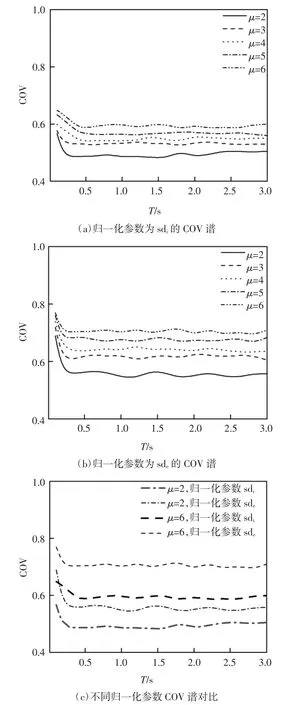
图6 等延性残余位移比COV 谱Fig.6 COV spectra of constant-ductility residual displacement ratios
4.3 强度折减系数的影响
强度折减系数α 为结构保持弹性所需的最小强度与屈服强度之比.分别取α 为2、3、4、5 和6,计算四类场地平均等强度残余位移比COV 谱,结果如图7 所示.可以看出:等强度残余位移比COV 谱分别随强度折减系数的增大而增大.等强度残余位移比离散性受归一化参数的影响较为显著,与sde作为归一化参数的残余位移比COV 相比,sdi作为归一化参数的等强度残余位移比COV 更小.这是因为选择与残余位移相关性较大的参数(sdi)对其归一化后得到的等强度残余位移比COV 更小.结构自振周期小于0.5 s 时,等强度残余位移比COV 随着周期增大而减小;结构自振周期大于0.5 s 时,等强度残余位移比COV 趋于不变,即周期大于0.5 s 时等强度残余位移比COV 谱对周期变化不敏感.
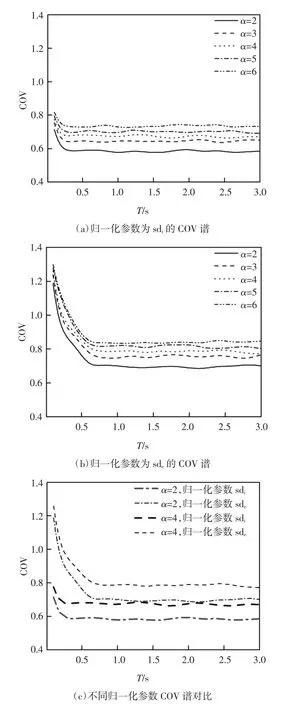
图7 等强度残余位移比COV 谱Fig.7 COV spectra of constant-strength residual displacement ratios
5 残余位移比变异系数谱拟合
本文通过回归分析建立残余位移比COV 谱拟合公式.正如前文所述,影响结构残余位移比谱离散性的因素较多.场地条件对残余位移比谱离散性的影响较小,而μ 和α 对残余位移比谱离散性的影响显著.本文建立残余位移比COV 谱的拟合公式时也必须考虑μ 和α 的影响.由图6 和图7 可以看出,等延性和等强度残余位移比COV 谱的各曲线具有较为统一的谱形,其谱函数表达式分别为式(2)和式(3).
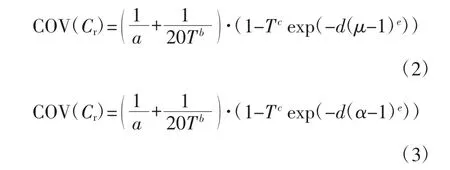
式中:参数a、b、c、d 和e 通过非线性最小二乘Levenberg-Marquardt 算法[26]回归分析得到,其值见表1.残余位移比COV 谱实际值和拟合值对比如图8 所示,可以看出本文构建的残余位移比COV谱的拟合公式能较为精确地预测结构残余位移比离散性.

表1 残余位移比COV 谱回归分析参数表Tab.1 Regression parameters of COV spectra of residual displacement ratios used in equation(2),(3)
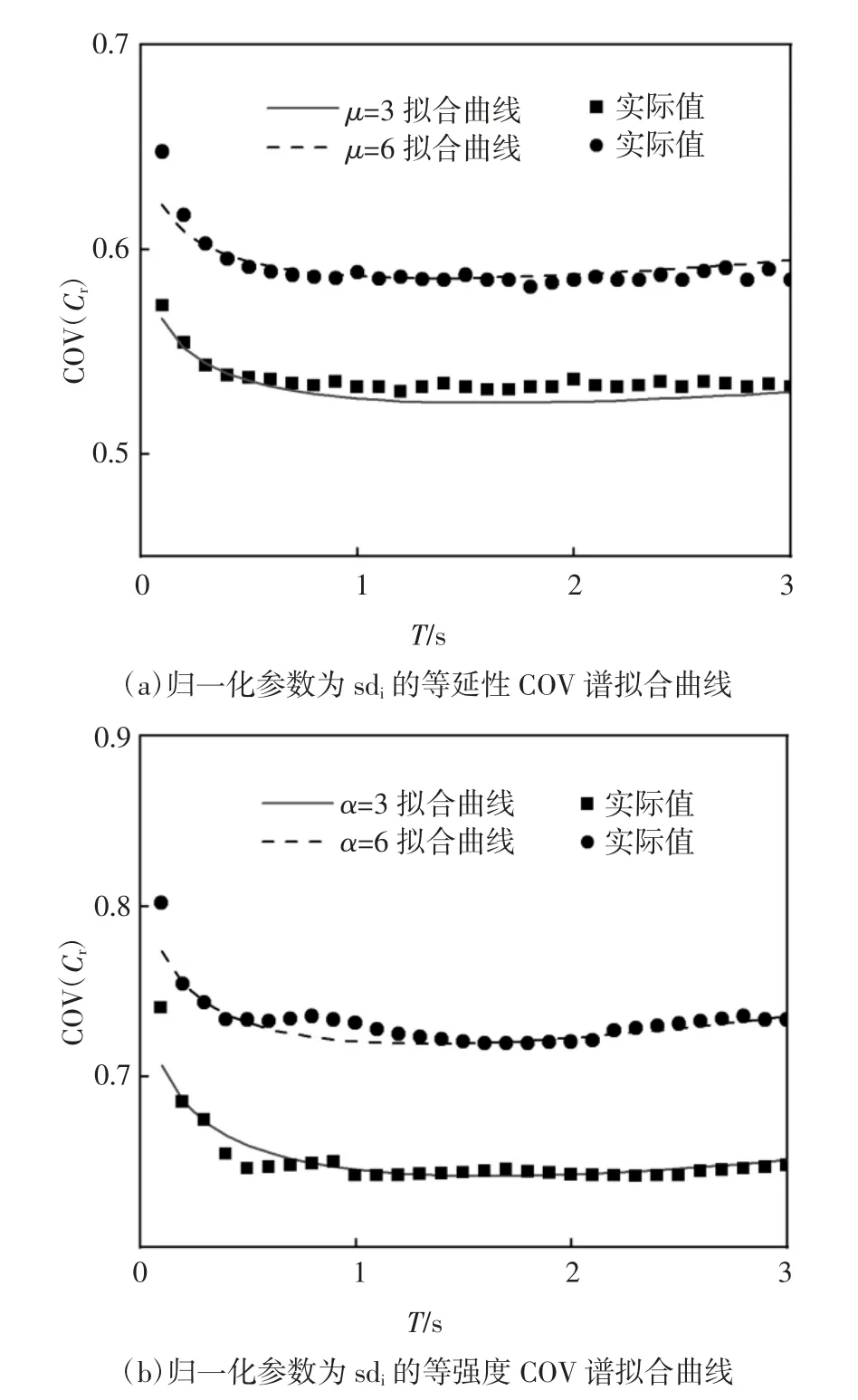
图8 等延性和等强度残余位移比COV 谱实际值和拟合值对比Fig.8 Comparison of COV spectra of residual displacement ratios computed using Eq(2)and(3)with the statistical results
6 结论
本文分析SDOF 体系残余位移与归一化参数(弹塑性谱位移、弹性位移)的相关性,基于大量地震动记录建立了等延性和等强度残余位移比变异系数谱,分析了延性系数、强度折减系数和场地类别对残余位移比谱离散性的影响.主要结论如下:
总体而言,残余位移与弹塑性谱位移的相关性较大,与弹性谱位移的相关性较小.这是因为弹性谱位移包含自振周期、阻尼以及反映结构弹塑性特征的参数(延性系数)等信息,而弹性谱位移中没有包含反映结构弹塑性特征的参数信息.残余位移与归一化参数的相关性受延性系数和强度折减系数的影响较小.
等延性和等强度残余位移比离散性受场地类别的影响较小.残余位移比变异系数谱分别随延性系数和强度折减系数的增大而增大.结构自振周期小于0.5 s 时,残余位移比变异系数谱随着周期增大而减小;结构自振周期大于0.5 s 时,残余位移比变异系数谱趋于不变.
等延性和等强度残余位移比离散性受归一化参数的影响较为显著.与弹性谱位移相比,弹塑性谱位移作为归一化参数得到的残余位移比变异系数更小.因此,选择弹塑性谱位移作为归一化参数可以减小结构残余位移比离散性.
致谢:感谢美国太平洋地震工程研究中心(PEER)NGA计划项目提供的地震动数据!

