汽轮机长叶片弹塑性分析及寿命评估方法

余德启　王恭义　李明

摘要： 在当前汽轮机的某些极限设计工况下，基于无限寿命的线弹性考核规范已经无法满足当前的工程设计要求，需要发展弹塑性强度计算方法以及有工程意义的强度评估准则，并在此基础上引入低周疲劳寿命考核方法对零部件寿命进行分析预测.对某汽轮机末级长叶片进行弹塑性有限元分析，提出将基于局部应力应变法的低周疲劳分析理论与商用疲劳分析软件相结合的方法对叶片进行强度设计的方法和流程.结果表明：所提出的弹塑性分析以及疲劳寿命评估方法能很好地反映长叶片的实际强度，有助于进一步制定一套完善的适合工程应用的长叶片强度评估标准，从而提高叶片的设计水平.

关键词： 汽轮机； 末级长叶片； 弹塑性； 局部应力应变法； 低周疲劳； 有限元

中图分类号： TK262； TB115.1文献标志码： B

Abstract： In some ultimate design conditions of current steam turbines， the linear elastic infinite life assessment specification is unable to meet the current engineering design requirements. The elastoplastic strength calculation method and the strength assessment criteria for engineering should be developed， based on which the low cycle fatigue life assessment method should be introduced into the analysis and prediction on the life of parts. The elastoplastic finite element analysis on the last stage long blade of a steam turbine is performed. Combing commercial fatigue analysis software with the low cycle fatigue analysis theory， based on local stressstress method， the blade strength design method and procedure are proposed. The results indicate that， the method of elastoplastic analysis and fatigue life assessment can well reflect the actual strength of blades， which is helpful to propose a perfect long blade strength assessment standard for engineering application and improve the long blade design level.

Key words： steam turbine； last stage long blade； elastoplasticity； local stressstrain method； low cycle fatigue； finite element

收稿日期： 2014[KG*9〗08[KG*9〗18修回日期： 2014[KG*9〗09[KG*9〗08

基金项目： 上海市科学技术委员会科研计划（13XD1422400）

作者简介： 余德启（1983—），男，河南固始人，工程师，硕士，研究方向为汽轮机产品设计开发，（Email）yudq@shanghaielectric.com0引言

汽轮机末级长叶片的出力通常占整个机组出力的10%以上，是汽轮机至关重要的部件，其设计参数直接影响电厂的运行效率和功率，故其安全运行性能必须得到有力的保障.叶片较易出现疲劳失效，其安全可靠性决定汽轮机的安全.[1]因此，汽轮机叶片疲劳寿命评估是汽轮机强度设计和安全性考核的重要内容[2]，疲劳寿命分析不但可以指导叶片优化设计，还可以为受损叶片提供修复方案.叶片的工作按照转速可以分为启动、稳定转动和停机3个阶段.在启动和停机过程中，叶片经历很大的离心变幅载荷以及同步的稳态汽动载荷，属于低周疲劳；在高速稳定运转过程中，叶片因承受汽流扰动产生的激振力而振动，幅值较小，但频率很高，属于高周疲劳.叶片的启动和停机过程是裂纹萌生和稳态扩展的主要因素，是整个生命周期分析的重点.CARTER[3]指出高周疲劳对结构疲劳寿命分析非常重要.汽轮机叶片设计时，均已考虑如何避免应力快速累积的高周疲劳，所以除非有初始缺陷或者处于小容积流量等特殊工况，否则汽轮机叶片失效中很少出现高周疲劳，而低周疲劳是汽轮机叶片失效的主要原因.

当前，结构强度校核多基于线弹性假设下的屈服强度准则：当结构应力超过屈服应力时，即认为结构失效.这种基于线弹性假设的屈服强度准则简单易用，但与工程实际中易发生的结构弹塑性变形和非线性应力不符.随着叶片结构大型化的发展以及在工作转速或者某些变工况情况下，叶片的部分区域有可能已经进入塑性变形区，使用线弹性假设估计结构应力、强度校核和疲劳寿命可能会带来误差甚至导致错误的判断，故不能全部按照常规弹性强度去考核，而需要引进弹塑性计算方法和考核标准进行有效的、有工程意义的考核.

本文将商用有限元软件ABAQUS作为弹塑性有限元分析工具，并结合低周疲劳寿命评估方法，对汽轮机叶片进行低周寿命评估.首先，通过与文献中的经典弹塑性问题、试验结果对比，辅助验证本文所用的弹塑性分析和寿命评估方法的正确性；然后，以某叶片为模型，对叶片进行弹塑性分析和寿命预估，有助于进一步制定完善的、适合工程应用的考核标准.

1弹塑性有限元方法

循环加载是很多重要设备的关键部件所承受载荷的主要形式，由其引起的循环塑性变形（塑性疲劳和断裂）是造成设备破坏的主要原因.局部塑性变形是裂纹萌生和扩展的先决条件，又由于局部应力与应变之间存在一定的关系，因此，决定零件疲劳强度和寿命的是应变集中处的最大局部应力和应变.循环加载条件下材料本构模型的建立和结构的弹塑性响应分析是广泛关注的课题. 因此，在通过试件材料试验获得循环特性数据后，引入弹塑性有限元法描述汽轮机叶片局部塑性区域的局部应力应变关系.

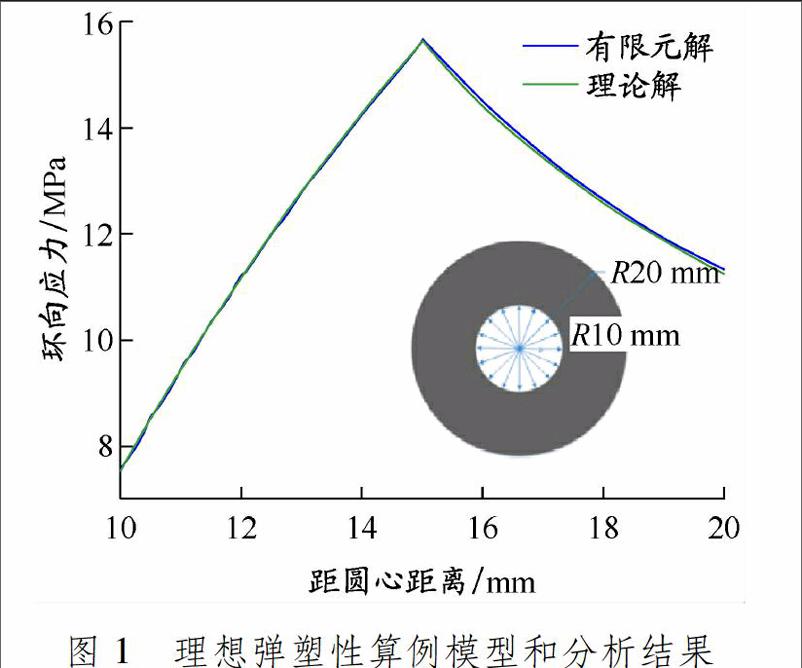
为辅助验证弹塑性有限元分析方法的正确性和可靠性，选取文献[4]中理想弹塑性和强化弹塑性算例为验证对象.其中，理想弹塑性算例为受压厚壁圆筒在理想弹塑性下的应力求解.受压厚壁圆筒的几何模型和分析结果见图1.由此可知：理想弹塑性的理论解与本文的有限元结果吻合.

强化弹塑性算例为T型接管三通在强化弹塑性下的应力求解.T型接管三通的有限元模型和分析结果见图2.

在T型接管三通的有限元计算中采用不同的网格精度，其分析结果与文献结果相吻合.通过理想弹塑性和强化弹塑性算例的验证，证明当前使用ABAQUS计算弹塑性问题所得结果的正确性.

2疲劳寿命分析方法

汽轮机叶运行环境极为复杂恶劣，并且汽轮机叶片的大部分寿命都消耗在疲劳裂纹的起始上，所以研究中一般都把裂纹起始寿命定义为叶片的疲劳寿命.疲劳寿命分析中使用的局部应力应变法所研究的就是叶片的致裂寿命.汽轮机叶片的实际使用寿命超过规定的疲劳寿命指标时，叶片中的疲劳裂纹扩展到叶片断裂还有一段时间，如果这时候及时对叶片进行全面检查，发现裂纹并且采取措施及时处理，那么就可以防止造成叶片断裂事故.

机械零件的疲劳破坏都是从应变集中部位的最大局部应变处首先开始，并且在裂纹萌生以前都要产生一定的塑性变形，局部塑性变形是裂纹萌生和扩展的先决条件.由于局部应力和应变之间存在一定关系，因此，决定零件疲劳强度和寿命的是应变集中处的最大局部应力和应变.由此提出的寿命估算方法就是局部应力应变法.使用局部应力应变法估算出的是零部件的裂纹形成寿命，这实际上与工程中经常使用的汽轮机叶片的疲劳寿命概念相吻合，并且零部件的致裂寿命往往可占构件使用寿命的80%左右.对于汽轮机叶片，这一比例将更高，所以使用局部应力应变法估算汽轮机叶片疲劳寿命是合适的.

汽轮机末级叶片材料的应变EN曲线为Δε2=σ′fE（2Nf）b+ε′f（2Nf）c（1）式中：E为弹性模量；σ′f为疲劳强度系数；ε′f为延性系数；b为疲劳强度指数；c为疲劳延性指数.弹性应变的EN曲线由E，b和σ′f共同确定，σ′fE为弹性应变EN曲线寿命为1时的截距，b表示曲线斜率；塑性应变的EN曲线由c和ε′f确定，ε′f为塑性应变EN曲线寿命为1时的截距，c表示斜率.

在疲劳分析过程中，平均应力影响可能较大，所以在计算时选择Morrow修正应变算法.Morrow修正算法主要用于基于应变的疲劳计算，公式为Δε2=σ′f-σmE（2Nf）b+ε′f（2Nf）c（2）式中：σm为平均应力.

3弹塑性分析和寿命评估方法验证

通过标准工业钢件试棒的数值分析和试验，考察本文所采用弹塑性有限元法和疲劳寿命评估方法的正确性.由于试件结构复杂，疲劳解析模型较难以获取，所以将物理试验与疲劳有限元分析相对应，疲劳算法主要考核疲劳破坏位置.

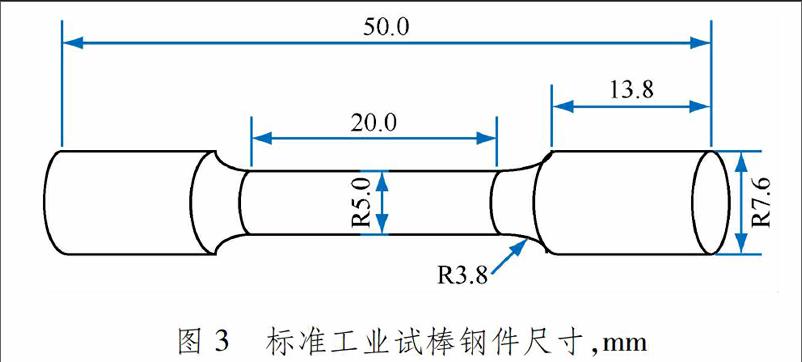
标准工业钢件试棒为柱形，尺寸见图3.材料的弹性模量为201.2 GPa，泊松比为0.281，塑性屈服应力为950 MPa，拉伸极限为1 056 MPa.钢件一端固定，另一端所受扭转角为0.15 rad.

标准工业钢件试棒线弹性和弹塑性计算应力分布见图4和5.结果显示：试件的中间段圆柱两端应力较高，线弹性计算最大应力为1 952 MPa，弹塑性计算最大应力为1 031 MPa.在考虑塑性的情况下，应力重新分布，计算的应力峰值降低.

标准工业钢件试棒线弹性和弹塑性计算寿命分布见图6和7.结果显示：中间段圆柱两端疲劳寿命较低（与有限元最高应力分布位置相同），线弹性计算最小寿命为24次， 弹塑性计算最小寿命为14 354次.在高应力情况下，考虑塑性导致应力重新分布、应力峰值降低，计算结果更可信：在只考虑弹性情况下，由于计算应力峰值接近（或超过）拉伸极限，导致计算结果中最小疲劳寿命较小；在考虑弹塑性情况下，材料塑性使计算应力峰值低于拉伸极限，计算寿命更真实，并且塑性引起的应力重新分布也使其寿命在构件中重新分布.

标准工业钢件试棒试验断裂图见图8.通过对比有限元计算结果与试验结果可以看出：标准工业钢件试棒有限元计算疲劳寿命最小处与试验断裂结果相符，可验证有限元计算的正确性；破坏位置与疲劳有限元分析结果一致，可以证明当前疲劳有限元计算可以准确捕获试件在受载荷情况下的破坏断裂行为.

4有限元分析和寿命评估

汽轮机叶片所承受的载荷有很多种，其中机组启动—运行—停机的循环对于汽轮机叶片是一种低周疲劳载荷.每一个循环都会使其产生一定损伤，这种损伤累积到一定程度即达到某个临界值时，叶片就会发生疲劳破坏，即为疲劳累积损伤.

对某汽轮机叶片在正常工作转速和超速10%这2种速度下，分别采用线弹性和弹塑性本构模型评估汽轮机叶片的疲劳寿命.

在进行汽轮机有限元计算时，由于汽轮机叶片整体模型复杂，计算代价较高，所以可以使用单扇区模型并施加周期性边界条件替代整圈模型，从而达到节约计算成本、提高计算效率的目的.汽轮机叶片的相邻叶片在叶片顶部和凸台位置处存在空隙（见图9a），若在单扇区叶片模型直接施加周期性边界条件，则会过高估计汽轮机叶片模型的整体强度，造成结果不真实[5]，所以对汽轮机单扇区叶片进行切割，切割修正后的模型见图9b.在空隙处施加接触关系，在切割面施加周期性边界条件，最后形成的整体模型见图9c.

基于线弹性本构和线弹性疲劳分析计算，在正常工作转速下，该汽轮机叶片最小寿命发生在叶片根部，为2.5万h（疲劳寿命以每百小时500次循环为基数计算）.线弹性疲劳计算结果表明在工作转速下汽轮机叶片较难发生疲劳破坏.此时，由于汽轮机叶片基本没有塑性应变，所以基于线弹性本构得出汽轮机叶片疲劳寿命结果与在弹塑性本构下所得结果基本相同.

由于篇幅所限，此处仅给出超速10%工况下叶片最危险位置处的寿命分布见图10和11.

在超速10%并基于线弹性假设下，该汽轮机叶片最小寿命为287 h.在超速工况下，弹塑性有限元分析和疲劳分析结果表明：汽轮机叶片根部先发生疲劳，最小寿命为2 040 h，与线弹性疲劳计算得到的汽轮机叶片最小寿命287 h相比，疲劳寿命增大，说明结构局部发生塑性变形后应力会重新分布，对叶片的寿命有利，弹塑性计算更贴近于工程实际.

5结束语

当前结构强度校核多基于线弹性假设下的屈服强度准则，当结构应力超过屈服应力时，即认为结构失效.这种基于线弹性假设的屈服强度准则简单易用，但与工程实际中易发生的结构弹塑性变形和非线性应力不符.随着叶片结构大型化的发展以及在工作转速或者某些特殊工况情况下，叶片的部分区域有可能已经进入塑性区，故不能全部按照常规弹性强度考核，需要引入弹塑性的计算方法和考核标准进行有效的、有工程意义的考核.

本文研究一种基于弹塑性有限元法和局部应力应变法的低周疲劳寿命分析方法，该方法可用于汽轮机长叶片的实际工程设计和寿命评估，对其他工程领域也有参考意义.

参考文献：

[1]周仁睦. 汽轮机叶片疲劳断面及事故分析[J]. 机械强度， 1982（1）： 1221.

ZHOU Renmu. Fatigue section and accident analysis of steam turbine blade[J]. J Mech Strength， 1982（1）： 1221.

[2]王恭义， 程凯， 杨建道， 等. 800 mm末级长叶片疲劳特性分析与寿命预估[J]. 热力透平， 2013， 42（1）： 4042.

WANG Gongyi， CHENG Kai， YANG Jiandao， et al. Fatigue characteristics analysis and life prediction of 800 mm last stage blades[J]. Therm Turbine， 2013， 42（1）： 4042.

[3]CARTER T J. Common failures in gas turbine blades[J]. Eng Failure Anal， 2005（12）： 237247.

[4]王勖成. 有限单元法[M]. 北京： 清华大学出版社， 2003： 598599.

[5]程凯， 徐芬， 王恭义， 等. 汽轮机叶片有限元分析中特殊边界的处理[J]. 华东电力， 2010， 38（11）： 17671770.

CHENG Kai， XU Fen， WANG Gongyi， et al. Treatment of special boundary condition in finite element analysis for turbine blade[J]. East China Electr Power， 2010， 38（11）： 17671770.