考虑组合作用的钢-混凝土组合梁抗剪承载力

丁发兴，王 恩，吕 飞，王莉萍，余玉洁，黄青玲，余志武

(1. 中南大学土木工程学院，湖南，长沙 410075；2. 湖南省装配式建筑工程技术研究中心，湖南，长沙 410075)

钢-混凝土组合梁通过栓钉将混凝土板和钢梁连接为整体共同受力，充分发挥了混凝土抗压强度高和钢材抗拉强度高的特点，具有轻质大跨、刚度大、承载力高和施工快速方便等优点[1−2]，广泛应用于建筑和桥梁工程领域中。

目前学者们对钢-混凝土组合梁的抗弯性能[3−10]以及纵向抗剪性能[11− 15]等方面进行了深入研究，然而对竖向荷载下钢-混凝土组合梁的抗剪性能研究相对较少[16−20]。由于组合梁相对于纯钢梁腹板高度小，当剪跨比较小或采用宽翼缘H型钢时，钢-混凝土组合梁竖向剪力有可能起控制作用[2]，因而有必要开展相关研究。聂建国等[16]开展了16组正弯矩区工字钢-混凝土组合简支梁抗剪试验，探讨钢-混凝土组合梁破坏形式与剪跨比关系，在试验基础上，采用ABAQUS有限元软件对正弯矩区钢-混凝土组合梁的截面抗剪承载力展开研究[17−18]，提出了钢-混凝土组合梁抗剪承载力计算公式；薛建阳等[19]开展了1组正弯矩作用下及3组负弯矩作用下工字钢-混凝土简支组合梁抗剪试验；规范GB 50017−2017[21]仅考虑钢-混凝土组合梁中的钢梁腹板抗剪作用，而对混凝土板的抗剪贡献忽略不计，造成钢-混凝土组合梁抗剪承载力低估，因此当前钢-混凝土组合梁的抗剪组合作用工作机理和界限剪跨比等仍需要深入研究，现有各种钢-混凝土组合梁抗剪承载力计算公式需要进行比较分析及优化。

为深入研究工字钢-混凝土组合梁抗剪性能，本文工作如下：1) 基于ABAQUS有限元软件，采用合理的混凝土塑性-损伤本构模型与钢材弹塑性本构模型，建立考虑栓钉工作性能的钢-混凝土组合梁抗剪三维有限元模型，通过试验验证与足尺模型算例分析，确定界限剪跨比；2) 开展不同剪跨比下钢-混凝土组合梁抗剪性能参数分析，揭示栓钉应力重分布规律和组合梁抗剪分担比例；3) 通过对素混凝土板与钢梁的抗剪承载力进行参数分析，提出了两者抗剪承载力计算公式，然后基于叠加原理提出考虑混凝土板和钢梁腹板与翼缘抗剪贡献的工字钢-混凝土组合梁抗剪承载力计算公式，并与已有各类公式进行比较。

1 有限元模型与验证

1.1 有限元模型

1.1.1 建模方法

以ABAQUS/Standard 6.14为工具建立钢-混凝土组合梁三维精细有限元抗剪模型，所建模型的边界条件与试验边界条件一致，按简支梁的约束条件进行处理，对试件采用两边对称线位移控制加载方式，并采用增量迭代法展开非线性分析。组合梁计算简图以及所建立的模型如图1所示。图1中：hc为混凝土板高度；wc为混凝土板宽度；hs为钢梁高度；ws为钢梁翼缘宽度；tw为钢梁腹板厚度；tf为钢梁翼缘厚度；L为组合梁计算跨度；h为组合梁整体高度；a为组合梁剪跨长度；λ为剪跨比，定义λ=a/h。混凝土板采用8节点的三维线性减缩积分实体单元(C3D8R)，钢梁采用4节点减缩积分壳单元(S4R)，栓钉采用三维线性梁单元(B32)，钢筋采用三维线性桁架单元(T3D2)，钢梁与栓钉建立在一个部件中；模型采用结构化网格划分技术进行网格划分，并对栓钉进一步细划分为5段～7段，有利于栓钉工作性能分析的开展。栓钉和钢筋通过内置的方式嵌入混凝土板中，使栓钉和钢筋节点的平动自由度与混凝土板一致、自由度自动耦合，保证栓钉、钢筋和混凝土板单元之间协同工作。钢梁与混凝土板之间的相互作用类型为表面与表面接触，二者法线方向的接触采用硬接触，而切线方向的接触单元采用无摩擦面-面接触，以钢梁壳单元为主面，混凝土单元为从面，用于消除钢梁与混凝土板接触面的粘结作用。

图 1 组合梁抗剪计算简图及有限元模型Fig.1 Shear calculation diagram and FE model of composite beam

1.1.2 本构关系

混凝土与钢材的本构关系分别为塑性-损伤本构模型[22]和弹塑性(硬化)本构模型，其中混凝土单轴受压/拉本构关系的具体表达式如下：

式中：fs为钢材的屈服强度；fu为钢材的极限强度，取fu=1.5fs；εy为钢材屈服时的应变，εst为钢材强化时的应变，εu为钢材达极限强度时的应变，取εst=12εy，εu=120εy，ζ=1/216。钢材弹性模量Es=2.06×105MPa，弹性阶段泊松比取0.285。

栓钉应力-应变关系具体表达式如下[12]：

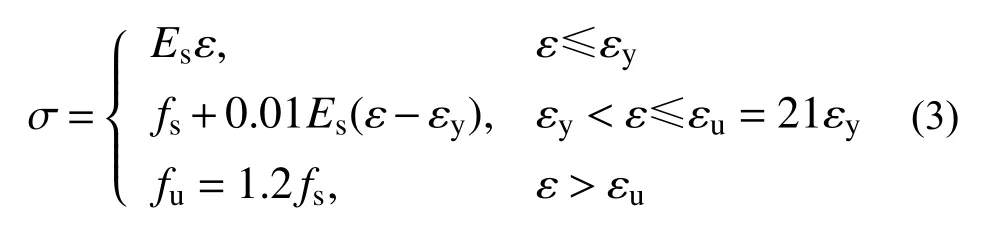
式中，取fu=1.2fs，Es=2.06×105。

1.2 试验验证

钢-混凝土组合简支梁抗剪有限元模型计算的剪力(V)-跨中挠度(δ)曲线与试验[16,19]曲线的比较如图2所示，可见有限元计算的刚度略微偏大且曲线略微偏刚。表1所示为钢-混凝土组合梁抗剪承载力有限元计算与文献试验结果的比较，表1中fsw为钢梁腹板屈服强度，fsf为钢梁翼缘屈服强度，Vu,t为抗剪承载力试验值，Vu,FE为有限元计算值。当计算V-δ曲线有下降段时，取计算曲线上的极值剪力为抗剪承载力；当计算V-δ曲线无下降段时，取试验V-δ曲线上峰值剪力对应的位移值所对应的有限元值作为极限抗剪承载力。如表1所示，Vu,t/Vu,FE均值为1.00，离散系数为0.05，表明本文有限元模型对工字钢-混凝土组合梁抗剪试件均模拟良好，如图2(a)～图2(e)所示。图3所示为组合梁试件CBS-9[16]有限元模型的应力云图，综合荷载-挠度曲线和应力云图可知，本文采用的钢-混凝土组合梁三维精细有限元模型对于组合梁的抗剪强度以及变形刚度均能够较准确地模拟。表2所示为钢梁抗剪承载力有限元计算与文献试验结果的比较。当采用实体单元进行模拟时，Vu,t/Vu,FE1均值为1.01，离散系数为0.04，当采用壳单元进行模拟时，Vu,t/Vu,FE2均值为1.01，离散系数为0.04，表明两种建模方法对工字钢梁抗剪试件均模拟良好，如图2(f)所示。

2 参数分析

建模过程中材料本构的选取与第1节中相同。钢材强度等级取Q235～Q420、混凝土强度等级取C30～C60。各足尺算例如表3所示，表中ds为栓钉直径，钢梁腹板厚度tw取16 mm～30 mm以保证钢梁腹板宽厚比不超限，钢梁翼缘厚度tf统一取20 mm，图4为12 m跨足尺组合梁算例截面示意图。

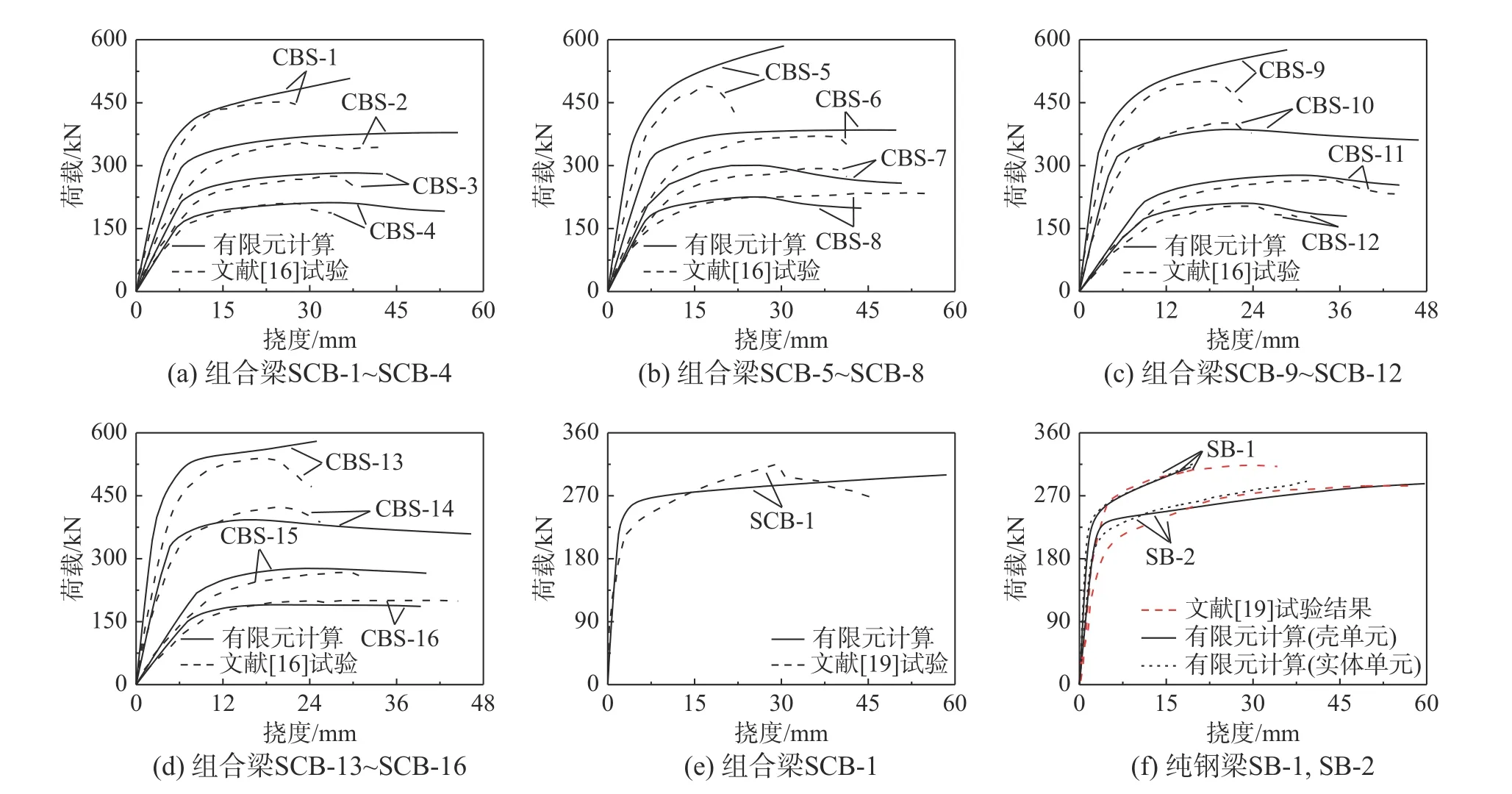
图 2 荷载-挠度曲线有限元结果与试验结果的比较Fig.2 Comparison of load–deflection curves between FE and test results

表 1 钢-混凝土组合梁抗剪承载力有限元计算结果与试验结果比较Table 1 Comparison between FE and test results of shear capacity of steel-concrete composite beams

2.1 剪跨比

剪跨比是影响工字钢-混凝土组合梁抗剪承载力的重要因素，图5给出了各计算跨度算例在不同剪跨比下剪力和弯矩的变化规律，可见：1) 当剪跨比λ=0.2时各算例抗剪承载力均达到最大值，因此可认为λ=0.2时有限元模型抗剪承载力计算结果作为工字钢-混凝土组合梁纯剪时的抗剪承载力V0.2；2) 随着剪跨比的增大，组合梁的抗剪承载力逐渐降低，在λ=1.5时，V/V0.2约为0.3～0.6，M/Mu在0.8以上且增长趋势变缓，此时抗剪不再起主导作用，在λ=3.0时，组合梁的纯弯段弯矩M几乎达到了极限弯矩值Mu，因此可认为λ=3.0为组合梁弯剪破坏与受弯破坏的界限剪跨比。

图 3 CBS-9试件模型应力云图 /MPa Fig.3 CBS-9 stress nephograms

2.2 几何尺寸和材料强度

为研究组合梁截面形式对抗剪性能的影响，以12 m跨算例为例建立有限元模型，栓钉布置间距为100 mm，材料组合采用C40配Q345，采用跨中两点对称集中加载方式，剪跨根据组合梁整体高度的变化来调整，以保证组合梁剪跨比固定为λ=0.2、λ=1.0、λ=2.0或λ =2.3，截面尺寸见表4，展开组合梁在不同截面形式细部参数hc、wc、hs、ws下的抗剪性能研究。

剪跨比分别为0.2、1.0、2.0或2.3时，12 m跨组合梁算例几何尺寸和材料强度等参数对抗剪承载力的影响规律如图6所示，可见：

1)剪力连接度η、横向配筋率ρst、纵向配筋率ρsl和计算跨度L对组合梁抗剪承载力几乎没有影响，如图6(a)～图6(d)所示；

2)混凝土强度fc、混凝土板宽度wc和混凝土板高度hc对组合梁抗剪承载力影响较小，如图6(e)～图6(g)所示，其中当混凝土强度fc提高两个等级时，组合梁抗剪承载力提高不足5%；当混凝土板高度hc从0.08 m增加到0.15 m，组合梁抗剪承载力提高不足5%；

表 2 钢梁抗剪承载力有限元计算结果与试验结果比较Table 2 Comparison between FE and test results of shear capacity of steel beams

3)钢梁屈服强度fs、钢梁翼缘宽度ws和钢梁高度hs对组合梁抗剪承载力有较大影响，如图6(h)～图6(j)所示，随着钢材屈服强度fs的提高，组合梁抗剪承载力有所提高，钢材强度fs从Q235提高至Q345时，组合梁抗剪承载力提高约35%，fs从Q345提高至Q420时，组合梁抗剪承载力提高约15%；钢梁翼缘宽度ws由0.3 m增加到0.6 m，组合梁抗剪承载力提高了39%左右；钢梁腹板高度hs由0.3 m增加到0.6 m，组合梁抗剪承载力提高了25%左右。

表 3 钢-混凝土组合梁算例参数Table 3 Parameters of steel-concrete composite beams

2.3 栓钉受力分析

以C30混凝土板配Q235钢梁、栓钉布置间距为60 mm的12 m跨有限元模型算例为基础，剪跨比分别为0.2、1.0和2.0时组合梁算例的各关键位置处栓钉受力随荷载的变化规律如图7所示，可见：

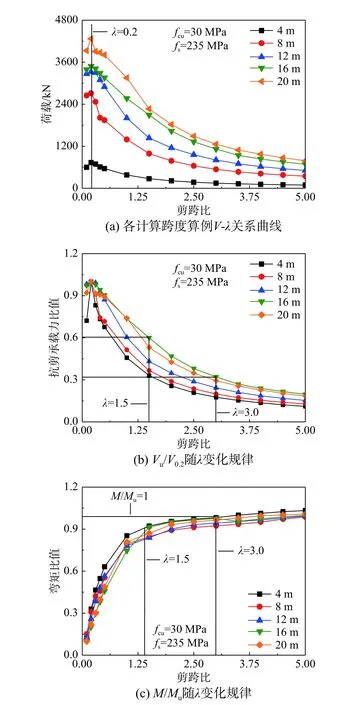
图 5 不同剪跨比下钢-混凝土组合梁剪力和弯矩的影响规律Fig.5 Influence of shear and moment on steel-concrete composite beams with different shear span ratios

表 4 算例截面尺寸Table 4 Sectional dimensions of calculation example

1)剪跨区的栓钉根部剪力和弯矩最大，而纯弯区的栓钉受力较小；剪跨比越大，栓钉根部受力越小；

2)随荷载增加，组合梁剪跨区内的栓钉应力值均不断增加，且0.6P荷载后剪跨区的栓钉受力明显进入塑性状态，栓钉根部达到屈服应力，如图7(d)、图7(e)所示；纯弯区栓钉与剪跨区的栓钉根部应力比值随着荷载与剪跨比的增大而不断增大，表明受力过程中组合梁的栓钉存在内力重分布现象，剪跨比越大栓钉内力重分布范围越广，如图7(f)～图7(h)所示。

2.4 组合作用对抗剪承载力影响

将相同剪跨比下纯钢梁和组合梁的抗剪承载力进行对比，对应的抗剪承载力增加幅度比较如图8所示，可见考虑混凝土翼板抗剪作用之后组合梁抗剪承载力可提升15%～40%，混凝土翼板对于组合梁抗剪承载力的贡献突出。

2.4.1 混凝土板

图9给出了剪跨比λ=0.2时组合梁中混凝土翼板和素混凝土板的抗剪性能比较，混凝土翼板和素混凝土板平均切应力τc(τc=Vc/Ac)随剪应变γc的变化规律如图9(a)所示，可见剪力作用下组合梁中混凝土翼板的平均切应力和延性得到了显著增长；二者破坏时切应力云图如图9(c)、图9(d)所示，可见混凝土翼板由于受到钢梁上翼缘的约束，破坏时切应力和塑性变形较大，而素混凝土板破坏时切应力和变形较小。

分别以8 m、12 m和16 m跨组合梁算例的混凝土板尺寸建立素混凝土模型，剪跨比取λ=0.2，不同混凝土强度下组合梁混凝土板与素混凝土板最大平均切应力比值τc1/τc2如图9(b)所示，可见组合梁中混凝土板的最大平均切应力为素混凝土板的0.9倍～1.4倍，平均为1.1倍，因此1.1倍可看成是钢梁对混凝土板的支撑作用导致混凝土抗剪承载力提高，即受剪荷载下钢-混凝土组合梁的组合作用提高了混凝土板的抗剪承载力，组合系数为1.1。

2.4.2 钢梁

图10给出了剪跨比λ=0.2时组合梁中的钢梁和纯钢梁抗剪性能的比较，钢梁和纯钢梁平均切应力τs(τs=Vs/As)随剪应变γs的变化规律如图10(a)所示，可以看出组合梁中的钢梁与纯钢梁受剪时的τs-γs曲线在弹性阶段几乎一致，此后纯钢梁变形增大而失稳破坏，组合梁中的钢梁稳定性好而保持很好的延性。

图 6 不同剪跨比下各参数对钢-混凝土组合梁抗剪承载力的影响Fig.6 Influence of parameters on shear capacity of steel-concrete composite beams under different shear span ratios

分别以8 m、12 m、16 m跨组合梁算例的钢梁尺寸建立纯钢梁实体模型，剪跨比取λ=0.2，不同钢材屈服强度下组合梁中的钢梁与纯钢梁最大平均切应力比值τs1/τs2如图10(b)所示，结果表明组合梁中钢梁的最大平均切应力为纯钢梁的0.9倍～1.2倍，平均为1.0倍。

2.4.3 抗剪承担比例

图 7 不同剪跨比下组合梁关键位置处栓钉受力随外荷载的变化规律Fig.7 Variation law of stud stress at key position of composite beam with external load under different shear span ratios

图 8 抗剪承载力提升幅度Fig.8 Increasing range of shear capacity

图11给出了12 m和20 m跨组合梁中钢梁和混凝土板各自剪力承担比例随剪跨比变化情况，可见组合梁中钢梁抗剪分担比例Vs/Vu约为70%～80%，混凝土板抗剪分担比例Vc/Vu为20%～30%，其抗剪作用不容忽略。

3 实用计算公式

3.1 素混凝土板抗剪承载力

以参数分析中涉及的足尺算例尺寸为基础建立素混凝土板有限元模型，剪跨比为λ=0.2，有限元分析结果如图12所示，素混凝土板平均抗剪强度τc计算公式可表示为：

则λ=0.2时素混凝土板抗剪承载力计算公式为：

3.2 纯钢梁抗剪承载力

图 9 破坏时组合梁中混凝土板和素混凝土板抗剪性能比较Fig.9 Comparison of shear behavior between concrete slab in composite beam and plain concrete slab

剪跨比为λ=0.2的纯钢梁破坏时的应力云图如图13所示，不同翼缘面积与腹板面积比值(Asf/Asw，Asf=2wstf,Asw=hwtw,hw=hs−2tf)下钢梁翼缘平均切应力τsf与腹板平均切应力τsw比值(τsf/τsw)变化规律如图14所示，结果表明钢梁翼缘平均切应力为钢梁腹板的0.3倍～0.45倍，均值为0.38，取下限值0.3，纯钢梁腹板抗剪强度按工字钢-混凝土组合梁规范[11]计算，则λ=0.2时考虑翼缘抗剪影响的纯钢梁抗剪承载力计算公式应为：

图 10 组合梁中钢梁与纯钢梁抗剪性能的比较Fig.10 Comparison of shear behavior between steel beam in composite beam and pure steel beam

图 11 组合梁中钢梁和混凝土板剪力分担比例Fig.11 Sharing proportion of shear capacity of steel beam and concrete slab

式(6)计算得到的λ=0.2时纯钢梁抗剪承载力Vs,EQ与有限元计算值Vs,FE的比较如图15所示，两者规律基本一致。

3.3 工字钢-混凝土组合梁抗剪承载力

λ=0.2时钢-混凝土组合梁的抗剪承载力由钢梁抗剪承载力与混凝土翼板抗剪承载力叠加所得：

式中，1.1为混凝土抗剪承载力的组合系数。

采用式(9)计算得到的λ=0.2时组合梁抗剪承载力V0.2,EQ与有限元计算值V0.2,FE的比较如图16所示，两者规律也基本一致。

图 12 素混凝土板抗剪强度变化规律Fig.12 Variation of shear strength of plain concrete slab

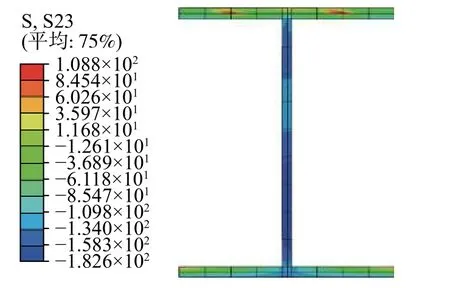
图 13 纯钢梁破坏时切应力云图 /mm Fig.13 Shear stress nephogram of pure steel beam

图 14 切应力比值-面积比值变化规律Fig.14 Variation of the shear stress ratio-the area ratio

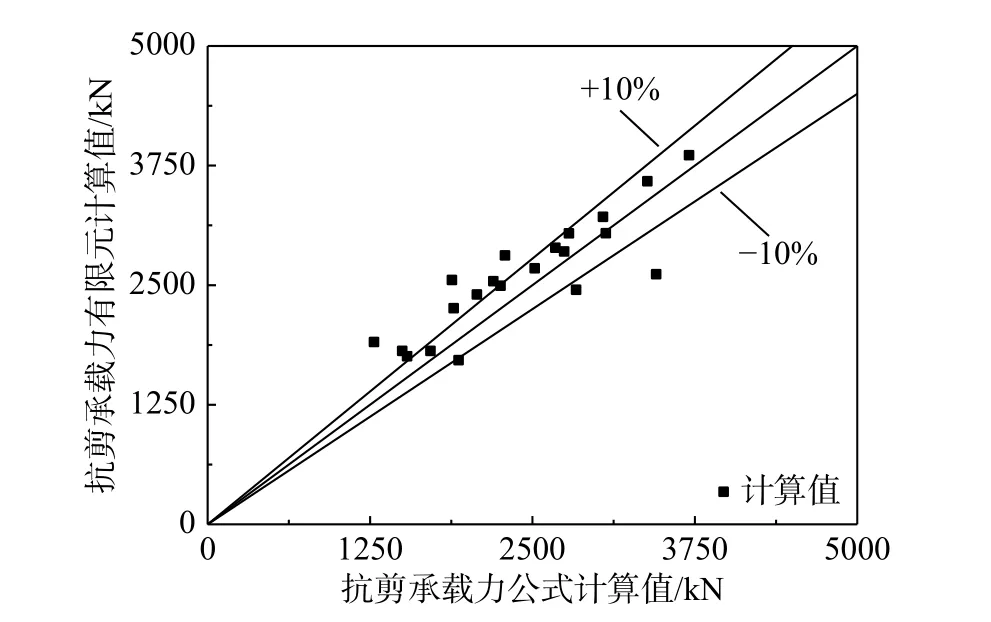
图 15 纯钢梁抗剪承载力计算结果比较Fig.15 Comparison of calculation results of shear strength of pure steel beams

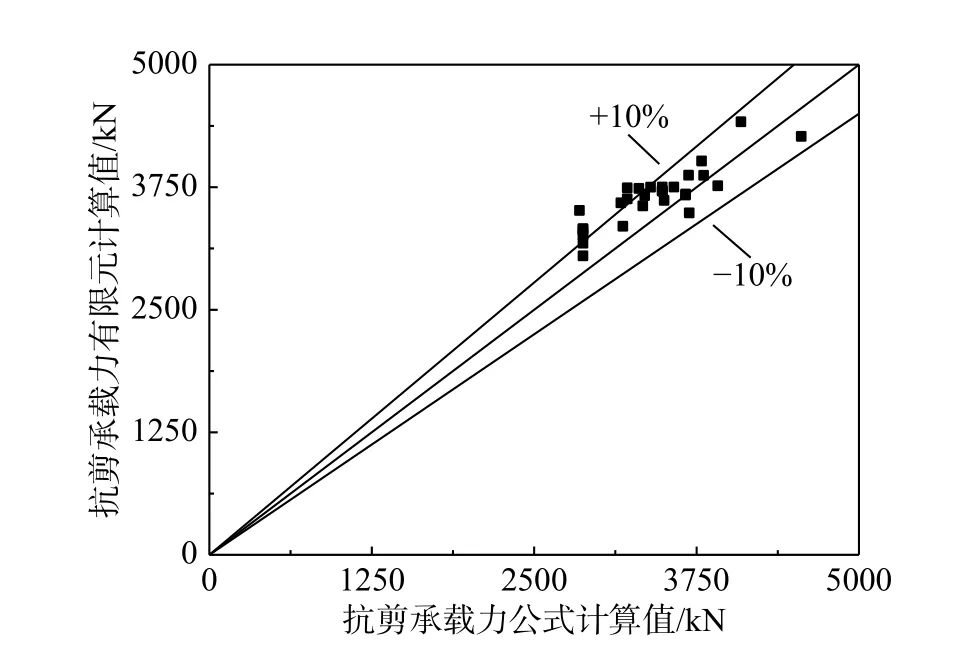
图 16 组合梁抗剪承载力计算结果比较Fig.16 Comparison of calculation results of shear strength of composite beams

不同剪跨比下钢-混凝土组合梁Vu/V0.2的关系如图17所示，经拟合得到：

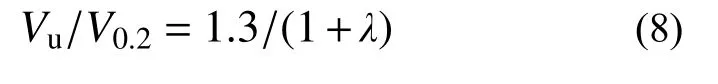
图 17 极限抗剪承载力-剪跨比关系曲线Fig.17 Curve of ultimate shear capacity and shear span ratio

经整合式(5)～式(8)，不同剪跨比下组合梁抗剪承载力计算公式可得到：

式中，λ取值范围为0.2～3.0，当λ>3.0时，按λ=3.0取值。混凝土强度等级范围为C30～C60，钢材屈服强度范围为235 MPa～420 MPa。

表5给出了GB 50017−2017建议的组合梁抗剪承载力计算式(10)，聂建国等建议的式(11)，可见式(11)考虑了钢梁腹板和混凝土翼板的抗剪作用，上述2个公式都没有考虑钢梁翼缘的抗剪贡献。将上述公式的计算结果(Vu,EQ)与文献[16, 19, 24]中的试验结果(Vu,t, λ=1.0～3.0)进行比较，结果比较散点图如图18所示，计算精度比较结果见表5，本文式(9)计算结果与试验结果的比值均值为1.05，离散系数为0.09，两者吻合较好，较其他公式离散性小。

GB 50017−2017建议的组合梁抗剪承载力计算公式(10)，聂建国等建议的公式(11)如下：

图 18 试验值与公式计算值比较结果Fig.18 Comparison of test value and formula calculation value

表 5 抗剪承载力试验结果与不同设计公式计算结果比较Table 5 Comparison of shear capacities between experimental and predicted results using different design methods

此外笔者以本文所建立的88组足尺有限元模型算例结果(Vu,FE)为对象，将各公式计算结果进行比较，结果比较散点图如图19所示，计算精度比较结果见表6，可见式(9)计算值与有限元值较为接近，均值为0.95，离散系数为0.10，较其他公式离散性小。

图 19 有限元与公式计算值比较结果Fig.19 Comparison of FE calculation value and formulas calculation value

表 6 试验结果和有限元计算结果与不同公式计算结果比较Table 6 Comparison between test results，FE results and predicted results using different design methods

4 结论

本文在试验验证准确的基础上建立多组足尺算例模型展开有限元分析，提出组合梁抗剪承载力实用计算公式，主要结论如下：

(1) 采用ABAQUS软件建立工字钢-混凝土组合梁抗剪有限元模型，以现有试验结果验证了所建立模型的准确性，并通过参数分析确定了工字钢-混凝土组合梁弯剪破坏与受弯破坏的界限剪跨比λ=3，同时分析结果显示抗剪荷载作用下组合梁中的栓钉存在内力重分布规律，即剪跨比越大，栓钉本身受力越小而内力重分布范围越广。

(2)钢-混凝土组合梁抗剪足尺有限元模型分析结果表明，混凝土翼板和钢梁翼缘对整体抗剪承载力具有一定的贡献，组合梁的抗剪承载力相比于纯钢梁提升约15%～40%，组合梁中混凝土翼板抗剪承载力分担比例约为20%～30%，钢梁翼缘平均切应力约为腹板平均切应力的0.3倍～0.45倍，混凝土翼板的最大平均切应力约为素混凝土板的1.1倍，组合梁钢梁的最大平均切应力与纯钢梁基本一致。

(3)通过足尺有限元模型的参数分析，根据叠加原理提出了考虑混凝土板和钢梁腹板与翼缘抗剪贡献的工字钢-混凝土组合梁抗剪承载力计算公式，以组合梁抗剪试验结果以及足尺有限元模型算例结果为依据，开展了规范以及各学者建议的钢-混凝土组合梁抗剪承载力计算公式的比较，结果显示笔者建议的公式具有良好的精度。