刚性弹侵彻有限直径金属厚靶的机理与模型研究
王 娟,赵均海,张建华,周 媛
(1. 长安大学理学院,西安 710064;2. 长安大学建筑工程学院,西安 710061)
空腔膨胀理论在弹靶撞击领域中有着广泛的应用,许多学者运用空腔膨胀理论对金属材料、岩石、混凝土和土壤等材料的侵彻问题进行了研究,得到了许多成果[1−11],然而,此类研究多是建立在半无限靶体或者有限厚靶体(考虑靶背自由表面影响)的基础上,对于有限平面尺寸靶体的系统研究还仅限于试验[12−13],理论分析很少查到,即使有,也大都忽略了靶体侧面边界对侵彻的影响。Littlefield等[12]的研究发现,当靶体尺寸较小时,这种假设带来的结果与试验数据偏差明显。鉴于此,2011年蒋志刚等[14]提出了有限柱形空腔膨胀理论,首次以系统的理论建立了长杆弹侵彻有限直径金属厚靶的侵彻理论模型;随后,宋殿义等[15]利用该理论建立了刚性尖头(卵形)弹侵彻柱形金属厚靶的侵彻模型。然而该模型由于仅针对单一弹头形状、采用的Mises准则只适合于剪切屈服极限和拉压屈服极限关系为τs=0.577σs的材料而有明显缺陷。此外,工程中常用于拉压强度相等材料的其他两个屈服准则:Tresca屈服准则(未考虑中间主应力的影响)和双剪应力屈服准则,也都只能适用于τs=0.5σs和τs=0.667σs的材料,适用范围有限。
统一强度理论考虑了作用于双剪单元体上的全部应力分量以及它们对材料破坏的不同影响,可以综合反映各种不同靶体材料基本强度特性,还可以体现强度准则差异的影响[9,16 −17],在国内外得到广泛的成功应用,所得终点效应计算公式与试验结果最为接近,是求解侵彻复杂应力状态问题更合理的新强度准则[7−8]。由于材料强度准则的建立和选用是研究靶材抗侵彻性能的重要环节,同时为了扩展材料的适用范围并充分发挥靶材潜能,本文采用统一强度理论,考虑中间主应力和靶体侧面自由边界的影响,推导弹塑性阶段和塑性阶段的空腔壁径向应力,建立线性硬化靶材的统一侵彻模型,求出适用范围更广、精确度更高的中低速(v0≤1000 m/s)刚性弹在侵彻有限直径金属厚靶时的侵彻阻力和侵彻深度计算公式,对半无限金属靶体的侵彻问题同样适用;将本文理论公式计算结果与弹道试验结果、其他公式结果进行了对比验证,文献[15]的结果仅是本文结论的一个特例;得到一系列基于不同强度准则的解析解,有效地预测了拉压强度相等的各类靶材在不同撞击速度下侵彻深度区间;将所得卵形弹侵深公式扩展至锥形弹和球形弹,研究了弹头形状对侵彻性能的影响;讨论了强度参数、强度准则差异、弹体撞击速度以及靶体半径对终点弹道性能的影响,可以为坦克、舰船等金属装甲防护设计及计算提供一定的参考和依据。
1 统一强度理论
统一强度理论是俞茂宏建立的一种全新的考虑中间主应力 σ2影响的适用于各种不同材料的统一强度理论。其数学表达式为[18]:


该准则是以b为参数的隐含了无限多个屈服准则的强度理论,因而也被称为双剪统一屈服准则[18]。
2 有限柱形空腔膨胀
2.1 基于统一强度理论的计算模型
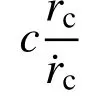

图 1 有限柱形空腔膨胀模型Fig.1 Finite cylindrical cavity expansion model


式中: σeq和 εeq分别为统一强度理论等效应力和等效应变; σr和 εr分别为径向应力和径向应变;σθ和 εθ分别为环向应力和环向应变。
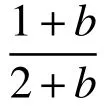

由于弹性区为小应变,塑性区为大应变,根据弹性区几何关系式及质点位移场表达式,可得[14]:

式中,r为t时刻空间坐标。
将式(5)代入式(4),可得线性硬化材料的有效应力-应变关系方程为:
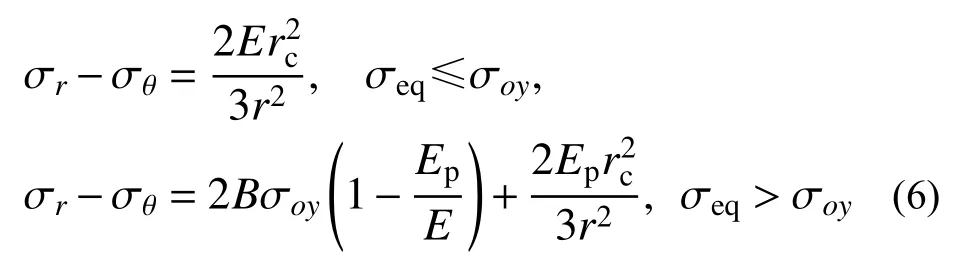
柱形空腔膨胀理论的速度场为[14]:

在柱坐标系下,靶体材料的动量守恒方程为:

式(6)~式(8)共同构成基于统一强度理论的不可压缩线性硬化材料的有限柱形空腔膨胀的基本方程。
2.2 空腔膨胀应力计算
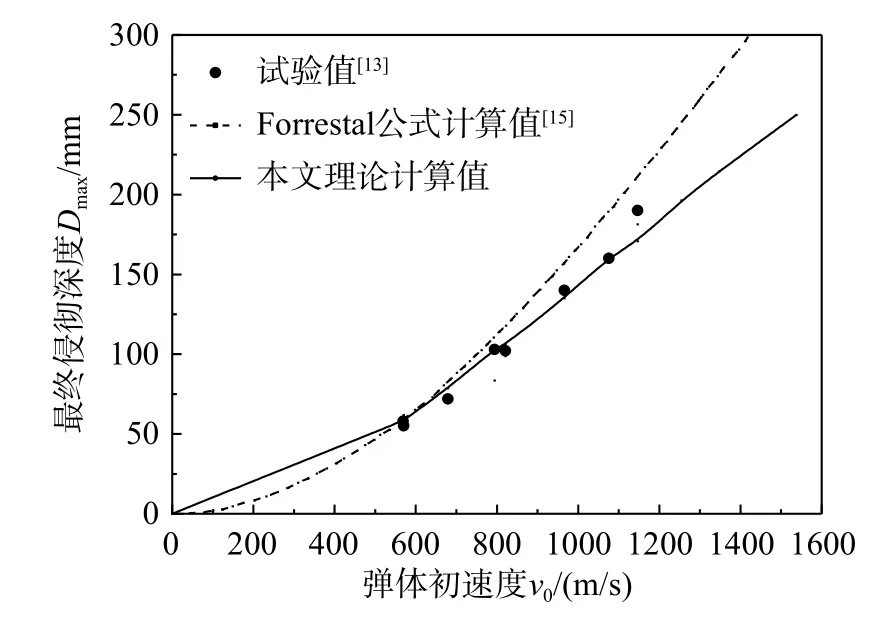
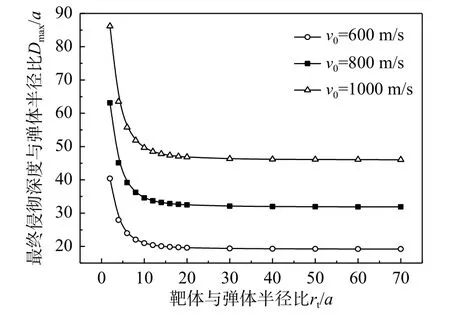
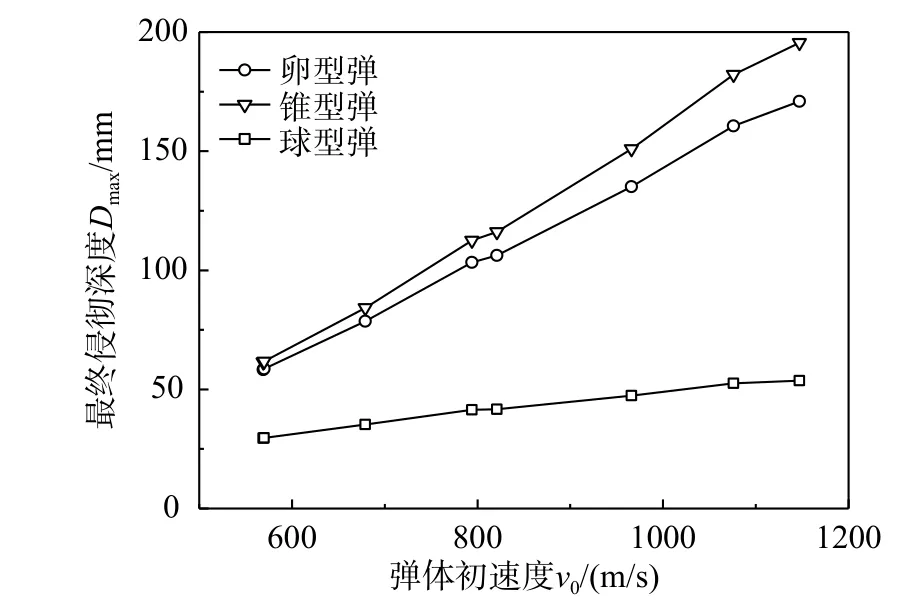
2.2.1 弹塑性阶段(rp 令rp=rt,此时第一阶段结束时的空腔膨胀半径rc1为: 在塑性区( σeq>σoy),将式(6)和式(7)代入式(8),整理可得: 对式(11)积分,可得: 式中,C1为一常数。 将式(13)代入式(12),求得径向应力 σr为: 在弹性区( σeq≤σoy),将式(6)和式(7)代入式(8),可得: 将边界条件 式中,rc2为第二阶段结束时的空腔半径。 基于Hill的塑性功假设[20 − 21]和有限柱形空腔膨胀问题的应力应变状态,有: 式中, εeq为统一强度理论的等效应变,可由式(22)和式(23)联合求解得到: 应变分量表达式为[14]: =εf条件,可确定α=1时,第二阶段结束时的空腔半径rc2为: 式中, εf为靶体材料的单向拉伸断裂应变。 2.3.1 刚性弹侵彻模型分析 假设刚性卵形弹旋转弹头母线方程为y=y(x);a表示弹体半径,l表示弹头长度,如图2所示。将弹丸的侵彻过程看成一系列空腔半径为rc=y(x) 、靶体半径为rt的有限柱形空腔膨胀模型来模拟[15]。假设弹丸初始速度和靶体初始侵深分别为v0和D0,t时 刻 弹 丸 速 度 和 靶 体 侵 深 分 别 为vt和Dt,那么t时刻靶体空腔半径rc和空腔膨胀速度vt分别为[15]: 图 2 侵彻模型尺寸Fig.2 Model dimension of penetration 2.3.2 侵彻阻力计算 忽略D 式中:φ为弹丸圆弧上一点的切线与弹丸轴线的夹角; σr(x)为根据本文有限柱形空腔膨胀理论计算所得的弹丸表面径向应力。 图 3 不同弹头形状的刚性弹Fig.3 Rigid projectiles with different nose shapes 将式(20)和式(21)分别代入式(28),可知: 假设当y(x1)=rc1时,x1为靶体刚到达弹塑性阶段末。当x1≥l时,a≤rc1,有限柱形空腔膨胀体只经历弹塑性阶段,侵彻阻力按式(29a)计算;当x1 联立式(27)和式(29),整理可得满足文献[15]的公式形式: 式(30)和式(31)中各项系数经计算整理得: 其中,Nd可以采用Simpson公式数值积分求得。 假设弹丸质量为m,根据文献[15]可知,由牛顿第二定律以及初始条件可得,t时刻弹丸侵彻有限柱形金属靶深度D为: 为了进行对比,取文献[13]中刚性卵形弹侵彻有限直径铝合金厚靶试验数据,代入本文公式进行分析讨论,弹体a=3.555mm ,l=11.8mm,L=59.3mm ,试验靶板为半径rt=127mm的6061-T6511铝合金,弹性模量为E=68.9GPa,切线模量为Ep=46MPa ,初始屈服应力为σoy=365MPa,密度为 ρ=2710kg/m。其他材料参数、试验值和理论计算值汇总见表1。 表 1 卵形弹侵彻有限直径金属厚靶数据汇总Table 1 Data summarization of ogive-nose projectile penetration into metallic thick target finite in radial extent 图4为根据文献[18]、计算比较后取强度参数b=0.4 时本文理论公式最终侵彻深度计算值Dmax与试验侵彻深度数据Dshi[13]、Forrestal公式结果[15]的对比曲线。由图4可以看出:本文理论公式计算值与试验值的平均相对误差为0.0094,均方差为0.0427;Forrestal公式结果[15]与试验值的平均相对误差为0.1469,均方差为0.0669。本文结果与试验数据吻合的更好,比Forrestal公式误差小了13.75%之多。由此验证了中低速(v0≤1000 m/s)弹侵彻有限直径金属厚靶时,本文理论计算模型具有一定的正确性和精确性。 图 4 侵彻深度对比Fig.4 Comparison of penetration depth 图5为文献试验中构件5(图5(a))和其他两个对比构件(图5(b)和图5(c))的射线照片[13],可以看到当v0=966 m/s时,侵彻结束时弹道笔直,并保持与靶体中心线一致,弹体没有明显变形,与本文理论计算模型假设(当弹体中低速(v0≤1000 m/s)撞击靶体时可视其为刚性弹[23−24])一致。当v0=1237 m/s时,弹道虽是直的,但与靶体中心线偏离了一定角度,弹体变形不太明显;当v0=1396 m/s时,弹道呈现曲线状,弹体轻微弯曲,图5(b)和图5(c)不再适用于本文计算模型。 图 5 侵彻弹道形态Fig.5 Radiographs of penetration craters 对于不同的材料,b的取值各不相同,可以求得一系列不同侵彻深度和靶体阻力解,即统一强度理论可以适用于多种材料。图6为不同b值时,所得侵彻深度Dmax与弹丸初速度v0的关系曲线。由图可以看出:强度参数b对最终侵彻深度Dmax有较大的影响,b值越大,中间主应力效应越明显,最终侵彻深度越小。这说明考虑中间主应力 σ2的影响,可以更加客观的表现出材料的强度潜能,使得构件发挥自身抗侵彻能力,侵彻分析及计算中不宜忽略。 图 6 不同 b值时侵彻深度对比Fig.6 Comparison of penetration depth with different b 同时,由于统一强度理论参数b还是选用不同强度准则的参数,当其取不同数值时,统一强度理论退化为不同的强度准则,由此所得的计算结果差别很大,以弹体着靶速度v0=569m/s为例,采用Tresca屈服准则(b=0)得到的侵深计算结果比采用双剪屈服准则(b=1)得到的侵深计算结果大22.45%,由此说明强度准则的选用对侵彻终点效应的预测也具有重要作用,实际工程应用中应选择合适的强度准则进行计算,从而更好地进行合理设计和节约材料。例如本文针对铝合金靶材取强度参数b=0.4进行计算,所得结果也代表了基于一种新的、针对此靶材更加合适的强度准则的解;若为其他靶材,可采用相同的方法,通过试验验证,取得适合自身的b值进行计算。 对于某一特定工况下有限直径金属厚靶侵彻问题,与其他计算方法只有唯一解不同,本文计算方法可以得到一系列解析解,文献[15]所得结果(Mises屈服准则结果)为本文b=0.366时的特例(只适合τs=0.577σs的材料),并且弹体侵彻深度的试验值几乎全部都会落在这一系列解析解范围之内。因此,采用本文理论计算方法可以得到某一特定工况下弹体侵深的上限值和下限值,有效地预测弹体侵彻深度的范围,例如,将计算结果归纳总结见表2,得到不同撞击速度下此类拉压强度相等靶材侵彻深度的预测区间。 表 2 不同撞击速度弹体侵彻深度预测区间Table 2 Penetration depth ranges for projectiles with different impact velocity 此外,由图6也可看出:当v0≤1147m/s时,弹体撞击速度越大,所得最终侵彻深度也越大。 图7为采用本文公式(b=0.4)所得不同撞击速度侵彻模型的侵彻深度D与弹体侵彻速度vt的关系曲线,由图可以看出:随着侵彻的进行,弹体速度不断减小,侵彻深度增加,但是侵彻深度增加的速率减小。 图 7 侵彻深度与弹体速度的关系Fig.7 Relationship between penetration depth and penetration velocity 其他条件均与试验数据一致,改变弹丸初始速度和靶体半径(即不同rt/a值),研究最终侵彻深度的变化情况,如图8所示(b=0.4)。计算过程中,当约rt/a≤10 时,a≤rc1,有限柱形空腔膨胀体完全经历弹塑性阶段和塑性阶段,侵彻阻力按式(29)两分式分段计算。当rt/a>10 时,a>rc1,有限柱形空腔膨胀体只经历弹塑性阶段,侵彻阻力按式(29)第一分式计算。由图8可以看出:随着靶体半径与弹丸半径比rt/a值的增大,最终侵彻深度与弹丸半径比Dmax/a值越来越小;当rt/a≥16时,侵彻深度与弹丸半径比减小的速度缓慢,rt/a=70 与rt/a=16相比,侵彻深度只减小了3.15%,但当rt/a<16时,侵彻深度随着靶弹半径比变化的程度显著,rt/a=4 与rt/a=16相比,侵彻深度增长了40.76%,说明当rt/a<16时,靶体边界尺寸的影响不能忽略,不能继续按照半无限靶体进行计算,与文献[13]试验结论相近。 图 8 最终侵彻深度与靶体半径的关系Fig.8 Relationship between final penetration depth and target radius 图9比较了弹杆直径相同的卵形弹头、锥形弹头和球形弹头作用下的理论侵彻深度(b=0.4),可以看出,弹头形状对侵彻深度的影响很大,锥形弹头的侵彻深度大于卵形弹头的侵彻深度,并且明显大于球形弹头的侵彻深度,当撞击速度小于570 m/s左右时,卵形弹头和锥形弹头所得侵彻深度基本相同。这是由于在保持弹杆直径和弹体长度相同的条件下,与锥形弹和卵形弹相比,球形弹的弹头相对平坦,弹头表面积相对更大,于是弹体在侵彻过程中受到的阻力也更大,进而使得侵彻深度明显较小,这说明了在相同弹杆直径和弹体长度的条件下,相比球形弹,锥形弹和卵形弹的穿透能力明显要强得多,其中锥形弹的穿透能力最强,当撞击速度小于570 m/s左右时,锥形弹和卵形弹穿透能力差别不大。 图 9 不同弹头形状侵彻深度比较Fig.9 Comparison of penetration depth with different projectile nose shapes 另外,由图9还可看出,各类弹体的侵彻深度均随着弹体着靶速度的增大而增大,只是相比球形弹,锥形弹和卵形弹的侵彻深度受弹体着靶速度的影响更为显著。 本文采用统一强度理论,研究了中低速刚性弹侵彻有限直径金属厚靶问题的侵彻机理和计算模型,并讨论了弹道终点效应的影响因素。主要结论如下: (1)本文建立的基于统一强度理论的有限柱形空腔膨胀模型考虑了靶体侧面自由边界、中间主应力效应和强度准则差异的影响,可以很好的描述整个侵彻过程中弹靶的动态响应;所得中低速弹体侵彻有限直径金属厚靶侵彻阻力和侵彻深度计算公式,适用于解决不同弹头形状的各类金属靶材的复杂应力状态问题,对半无限金属靶体的侵彻问题同样适用。将本文理论计算结果与弹道试验、其他公式结果进行比较,本文结果精度更高。 (2)采用本文理论计算方法可以得到一系列基于不同强度准则的解析解,从而有效预测不同撞击速度下拉压强度相等的各类靶材侵彻深度的区间,文献[15]所得结果仅为本文b=0.366时的特例。强度参数b对侵彻计算结果有非常大的影响,即考虑中间主应力效应,可以更加客观的表现出材料的强度潜能,使得构件发挥自身抗侵彻能力。 (3)弹体初速度和靶弹半径比对侵彻计算结果的影响较大。rt/a≤10时,有限柱形空腔膨胀体完全经历弹塑性阶段和塑性阶段,而rt/a>10时,有限柱形空腔膨胀体只经历弹塑性阶段;随着rt/a值的减小,Dmax/a值不断增大,当rt/a<16时,Dmax/a值增大的程度显著,此时靶体边界尺寸对侵彻终点效应的影响很大,不能继续按照无限大靶体进行分析计算。 (4)弹头形状对侵彻深度也有一定影响,就侵彻性能而言,锥形弹强于卵形弹,并且明显强于球形弹。



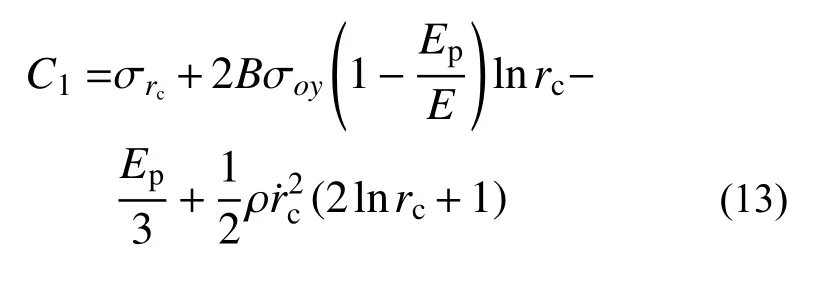


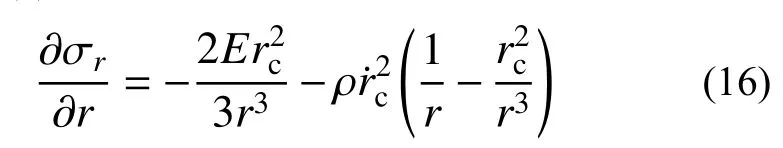
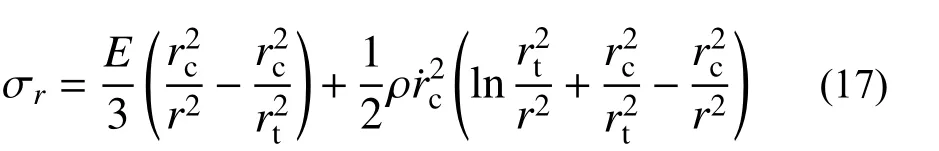


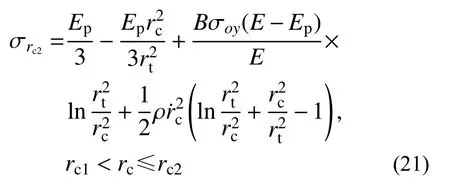
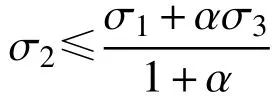

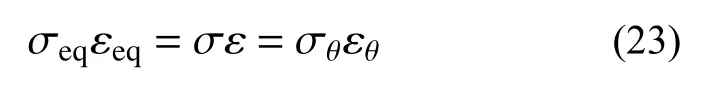






2.3 刚性弹侵彻柱形金属厚靶效应



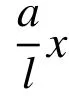



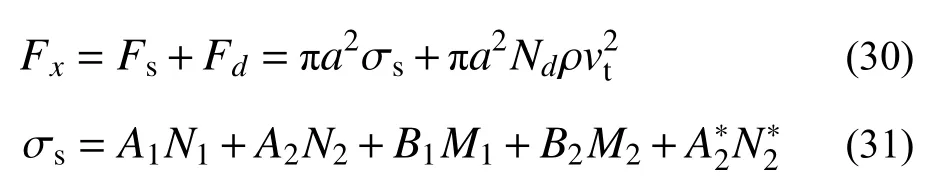

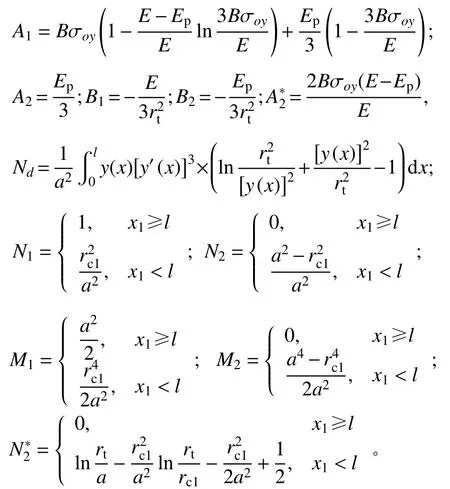
2.4 侵彻深度计算

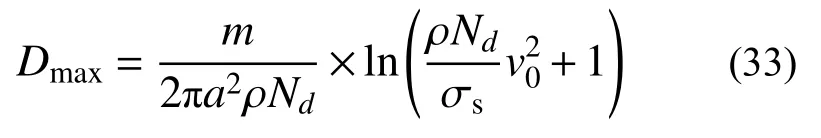
2.5 试验验证和结果分析


2.6 参数讨论



3 结论

