高延性混凝土加固蒸压加气混凝土砌体墙抗震性能试验研究

邓明科，马向琨，张 伟，李 宁

(1. 西安建筑科技大学土木工程学院，西安 710055；2. 华陆工程科技有限责任公司，西安 710065)

蒸压加气混凝土(autoclaved aerated concrete，AAC)砌块砌体具有自重轻、保温性能好、节约能耗等优势，在村镇建筑中具有广泛的应用前景。但由于自身强度低，抗裂性能差，AAC砌体作为承重墙体时，抗震性能较差，目前主要应用于填充墙等非结构构件中。此外，我国最新颁布的地震区划[1]对房屋建筑的整体抗震设防要求有所提高，而村镇砌体结构的施工质量差且构造措施不完善，因此，为了使AAC砌体结构具有满足设防要求的抗震性能，从而更好地推广应用此类结构，开展AAC砌块砌体墙的抗震加固研究具有重要意义。

国内外相关技术规程和标准规定了新建AAC墙体材料及施工方面的要求[2−4]，文献[5 − 6]研究了在墙体内部增设芯柱及构造柱等构造措施来改善其抗震性能。文献[7 − 9]分别研究了粘贴纤维织物、织物增强砂浆(textiles reinforced mortar，TRM)加固AAC砌体墙的抗震性能，研究表明，粘贴纤维织物可提高AAC墙体的承载力及变形能力，但存在耐久性较差及造价高等问题；TRM加固未能有效改善AAC墙体的脆性破坏模式。

传统的砌体结构抗震加固方法[10−12]存在增加结构自重、耐久性较差、对原结构扰动大等较突出的问题，因此不适用于现有AAC砌体墙的抗震加固。目前，工程水泥基复合材料(engineered cementitious composite，ECC)已应用于砌体结构加固领域，并取得了良好的加固效果[13−18]，为推广其应用，本课题组采用ECC设计理论制备了高延性混凝土(high ductility concrete，HDC)，在拉伸和剪切作用下表现出高延展性，具有典型的多裂缝开展和应变硬化特征，并对其加固砖砌体墙的抗震性能开展了系统研究[16−23]。研究表明，HDC面层及构造带加固方式可提高砌体墙的整体性，改善砌体墙的脆性破坏模式。

为探究一种经济有效、施工方便且适用于广大村镇AAC砌体墙的加固方法，本文提出采用HDC单面加固、双面条带加固及双面配筋条带加固AAC砌体墙的方式，通过低周反复荷载试验，分析各加固墙体的破坏形态、滞回性能及刚度退化；研究不同加固方式对AAC砌体承重墙抗震性能的影响，并且根据各试件的破坏形态给出了相应的承载力计算公式，为此类结构的加固设计提供依据。

1 试验概况

1.1 试件设计与制作

试验共制作了6片AAC砌块砌体墙，包括4片无构造柱墙体和2片构造柱约束墙体。试件AWG-0和AWG-1为构造柱约束墙体，其余均为无筋砌体墙。试件AW-0和AWG-0为未加固试件，试件AW-1和AWG-1均采用单面压抹15 mm厚HDC面层加固，试件AW-2和AW-3分别采用双面20 mm厚HDC条带和双面20 mm厚HDC配筋条带加固，配筋条带中竖向钢筋为φ6@120 mm，水平分布钢筋为φ6@300 mm，两侧条带用φ6@300 mm拉筋拉结。各试件的加固方式详见表1。

表 1 加固方式Table 1 Retrofitting form of specimens

墙体由钢筋混凝土加载顶梁、蒸压加气混凝土砌体墙及底梁构成。墙体的高宽比为0.62，构造柱截面尺寸为120 mm×190 mm，构造柱内纵筋为4φ6，箍筋为φ6@200 mm，试件的详细尺寸见图1。为提高墙体与HDC加固层的粘结性能，加固之前先对墙体水平灰缝进行勾缝处理(剔凿8～10 mm深度的灰缝)，再压抹HDC加固层。

1.2 试验材料

图 1 试件尺寸 /mmFig.1 Details of specimens

试验墙体均采用A5.0级AAC砌块和水泥砂浆砌筑，砌筑砂浆的厚度为10 mm。试验选用的AAC砌块的主要块型为600 mm×240 mm×190 mm，按标准试验方法[2]测得其立方体抗压强度平均值为3.5 MPa。砌筑砂浆及构造柱混凝土的抗压强度分别采用边长为70.7 mm和100 mm的立方体试块，与墙体同条件养护28 d后测定，测试结果见表2。本次试验中所用钢筋均为φ6，试验测得其屈服强度平均值为375 MPa。

表 2 材料实测强度Table 2 Measured strength of materials

HDC为粉煤灰、水泥、矿物掺合料、砂和PVA纤维等按一定比例配制而成，其中PVA纤维的体积掺量为1.7%，PVA纤维的各项力学性能指标见表3；由边长为100 mm的立方体试块测得的HDC抗压强度平均值为59.80 MPa；采用三个尺寸为350 mm×50 mm×15 mm的哑铃型试件测试HDC的抗拉强度和拉应变，其抗拉强度平均值为3.89 MPa，极限拉应变最大值达到1.25%。其中一个试件的单轴拉伸应力-应变曲线如图2所示。

表 3 PVA纤维各项性能指标Table 3 Performance indicators of PVA

图 2 HDC应力-应变曲线Fig.2 Stress-strain curves of HDC

1.3 加载制度及测点布置

本次试验采用拟静力试验加载方法[24]，并采用荷载-变形双控制分级加载。加载初期采用荷载控制，并分级加载，荷载级差为10 kN；当荷载-位移曲线明显弯曲后采用位移控制，位移级差为2 mm，且每级反复推拉3次，直至AAC砌体墙承载能力下降至极限荷载的85%以下，停止试验加载。

试验加载装置如图3所示。在加载梁中部布置一个位移计，以测试AAC砌体墙的顶点水平位移；底梁端部布置一个位移计，以测试墙体的整体滑移；墙面沿对角线方向布置两个位移计，以测试墙体的剪切变形。

图 3 加载装置Fig.3 Loading device

2 试验结果及分析

2.1 破坏过程

2.1.1 无构造柱试件

规定加载过程中荷载与位移的数值均以推方向为正、拉方向为负。

1)试件AW-0

当加载至90 kN时，墙体底部出现水平裂缝；随后，裂缝逐渐延伸；加载至110 kN时，荷载-位移曲线明显弯曲，改为由位移控制加载。加载至2 mm时，墙体出现阶梯状裂缝，并沿墙体对角方向延伸；加载至4 mm时，试件达到峰值荷载132.3 kN，此时，墙面形成多条斜裂缝，最终形成交叉斜裂缝；加载至8 mm时，斜裂缝宽度达8 mm，且局部砌块掉落，荷载降至峰值荷载的85%以下，试验停止加载。

2)试件AW-1

当加载至100 kN时，墙体底部出现弯曲裂缝；加载至−110 kN时，荷载-位移曲线弯曲，改为由位移控制加载。当加载至4 mm时，墙体达到峰值荷载170.6 kN，未加固侧底层砌块多处被压碎；加载至−4 mm时，HDC面层底部裂缝贯通且墙体产生了明显的滑移；当顶点位移达到14 mm时，加固面层底部水平裂缝宽度达10 mm，水平荷载仍无明显下降，此时，试验停止加载。

3)试件AW-2

当加载至−100 kN时，墙体南侧面底部出现水平裂缝；加载至120 kN时，试件南侧面出现斜裂缝，且荷载-位移曲线弯曲，此后试件按位移控制加载。当加载到2 mm时，HDC条带加腋处出现少量斜裂缝；加载至4 mm时，墙体达到峰值荷载145.6 kN，此时，HDC条带加腋处斜裂缝延伸变宽；随着位移增大，北侧条带开始剥离；当加载至8 mm时，北侧条带大面积脱落，荷载明显下降，试验停止加载。

4)试件AW-3

峰值荷载前，试件AW-3与试件AW-2现象类似。峰值荷载后，HDC条带加腋处裂缝变宽；此后随顶点位移增加，墙体南侧面中部灰缝裂缝贯通；当顶点位移达到14 mm时，HDC条带加腋处斜裂缝延伸至顶梁且面层外鼓，荷载明显下降，停止加载。

2.1.2 带构造柱试件

1)试件AWG-0

当加载至70 kN时，墙体底部出现水平裂缝；加载至−110 kN时，墙体出现斜裂缝，位移-荷载曲线弯曲，改为由位移控制加载。当加载到2 mm时，墙体斜裂缝变宽并延伸至构造柱；当加载至4 mm时，主斜裂缝相交，试件达到峰值荷载119.67 kN；加载至−4 mm时，两侧构造柱出现新的水平裂缝；此后随顶点位移增加，裂缝延伸变宽，当加载至12 mm时，墙体裂缝最大宽度达7 mm；当加载至14 mm时，墙体角部砌块压碎，水平荷载降至峰值荷载的85%以下，试验停止加载。

2)试件AWG-1

峰值荷载以前，试件AWG-1与试件AWG-0试验现象相似；峰值荷载后，随位移增加，两侧构造柱与砌体墙交接处，HDC面层出现竖向裂缝，并且未加固墙面根部出现受压裂缝；加载至10 mm时，面层两侧竖向裂缝扩展，且未加固墙面底部砌块压碎；此时，水平荷载明显下降，试验停止加载。

各试件破坏时的裂缝分布如图4所示。

2.2 破坏形态分析

1) 试件AW-0发生对角剪切破坏，墙面出现大量斜裂缝，表现出明显的脆性破坏特征。

2) HDC面层提高了墙体的对角剪切强度并限制了墙体的开裂，试件AW-1墙面未出现裂缝。墙体底部首先出现弯曲裂缝，且轻微摇摆；随后，底部水平裂缝逐渐贯通，未加固侧底部砌块压碎，墙体沿底部滑移；试件AW-1最终发生剪切滑移破坏，终止加载时，试件的水平荷载未明显下降。

图 4 试件的裂缝分布Fig.4 Crack distribution of specimens

3) 相比试件AW-3，试件AW-2缺乏锚固措施，因HDC条带与AAC墙体材料性能不同，在荷载作用下二者变形不协调，条带因内侧边缘处缺乏约束，首先在此处发生剥离；加载后期，HDC条带受压外鼓，进一步导致条带剥落，使得试件承载力迅速下降；随位移增加，墙面斜裂缝延伸、变宽，试件发生对角剪切破坏；相比试件AW-0，试件AW-2墙面裂缝数量明显减少。

4) 试件AW-3最终发生对角剪切破坏；相比试件AW-2，HDC配筋条带与墙体粘结较好，可为试件AW-3提供较好的约束，明显减小墙体的损伤，改善墙体的破坏形态。

5) 试件AWG-0最终发生对角剪切破坏，墙面出现多条斜裂缝，且构造柱出现弯曲裂缝；构造柱可为墙体提供约束作用，因此，相比试件AW-0，试件AWG-0破坏时墙面裂缝数量明显减少，损伤程度较轻。

6) HDC面层良好的约束效果使得试件AWG-1墙体底部首先出现水平裂缝，峰值荷载前，面层未发生破坏。由于砌块与构造柱强度差异大，峰值荷载后，弯曲作用使得此处砌块被压碎，导致HDC面层外鼓、开裂，出现两条竖向裂缝；未加固墙面出现数条斜裂缝，并且不断延伸、变宽；墙体最终发生弯剪破坏，相比试件AWG-0，试件AWG-1破坏时墙面裂缝数量明显减少。

2.3 滞回曲线及骨架曲线

图5给出了6个试件的荷载-位移滞回曲线，由图5分析可得：AAC墙体在开裂前，荷载-位移曲线基本呈直线；开裂后，墙体进入弹塑性变形阶段，曲线斜率逐渐减小，墙体刚度下降；相比未加固试件，加固试件的破坏模式有所改善，滞回曲线更加饱满，说明试验所采取的加固方式能有效提高AAC砌体墙的滞回性能。

1) 试件AW-0滞回环数量较少，墙体开裂后滞回环面积即显著增大，捏缩效应显著；HDC单面加固试件AW-1的弹性变形能力明显提高，峰值荷载后，墙体底部滑移且部分砌块被压碎，导致滞回环捏拢现象明显，但其数量及所围面积均有所增加，表现出较好的耗能能力；HDC条带的约束作用使得试件AW-2承载力有所提高，但峰值荷载后条带剥离，导致承载力迅速下降，曲线整体与试件AW-0相似；相比试件AW-2，试件AW-3的滞回环更加饱满，呈“弓”型，且数量明显增加，反映出较好的变形和耗能能力，因此，HDC配筋条带可为墙体提供较好的约束。

2) 相比试件AW-0，构造柱的约束作用使得墙体AWG-0的滞回环数量增加但捏拢现象更加明显；对于试件AWG-1，峰值荷载后墙体两侧砌块被压碎，导致承载力迅速下降；相比试件AWG-0，HDC面层改变了试件AWG-1的破坏模式，其水平承载力明显提高，滞回环数量有所减少但所围面积增大。

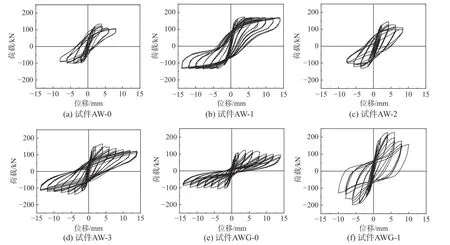
图 5 滞回曲线Fig.5 Hysteretic curves

各试件的骨架曲线如图6所示。取墙面出现第一条可见裂缝时所对应的荷载和位移确定其开裂荷载和开裂位移；根据“能量等值法”确定各试件的屈服荷载和屈服位移；由试验停止加载时的位移确定试件的极限位移。各试件在上述特征点处的荷载及位移见表4。由图6和表4分析可得：

1) 试件AWG-0的极限位移和位移延性系数分别为试件AW-0的1.74倍和1.81倍，说明构造柱的约束作用可大幅提高墙体的变形能力。

2) 对于无构造柱试件，加固试件的开裂荷载、峰值荷载均有所提高，且峰值荷载后的强度退化较为平缓。相比试件AW-0，试件AW-1、AW-2和AW-3的峰值荷载分别提高了31%、17%和28%，极限位移分别提高了74%、5%(条带剥离)和75%；加固试件AW-1、AW-3的位移延性系数分别提高了40%和66%。

3) 相比试件AWG-0，试件AW-3的峰值荷载提高了32%，且极限位移与之相近，说明HDC配筋条带可发挥类似圈梁-构造柱对墙体的约束作用，从而提高墙体的水平承载力与变形能力。

4) 对于构造柱约束试件，相比试件AWG-0，试件AWG-1的开裂荷载及峰值荷载分别提高了57%和86%，且试件AWG-1的残余承载力高于试件AWG-0的峰值荷载，说明试件可继续承受荷载，其变形能力尚未得到充分发挥。

图 6 骨架曲线Fig.6 Skeleton curves

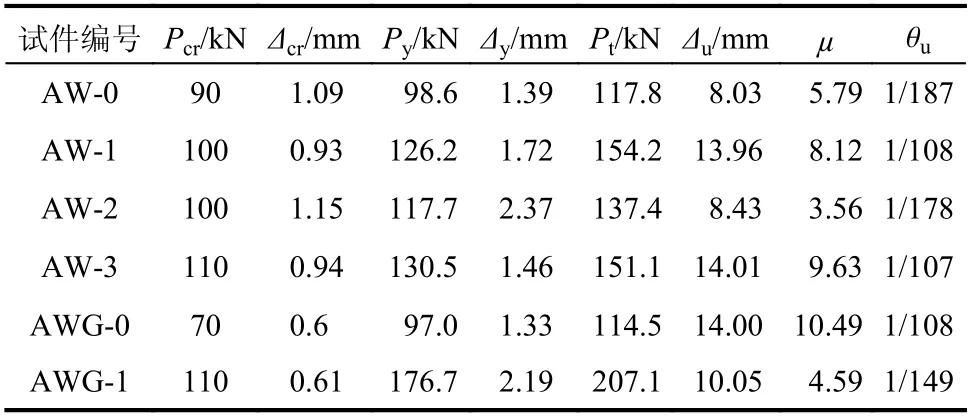
表 4 各试件特征点Table 4 Characteristic points of specimens

2.4 刚度退化

以各加载级割线刚度与其所对应的顶点位移变化曲线来研究各试件在加载过程中的刚度退化规律，如图7所示。

1) 对于无构造柱试件，峰值荷载后，单面加固及双面配筋条带加固墙体的刚度退化曲线相对平缓，说明此类加固方法可延缓无筋AAC墙体的刚度退化；由于HDC条带剥离，试件AW-2的刚度退化曲线与试件AW-0较为接近。

2) 对于带构造柱试件，由于HDC面层的约束作用，试件AWG-1的初始刚度大幅提高，加载初期的刚度退化明显；峰值荷载后，墙体根部砌块压碎，HDC面层外鼓，导致其刚度退化较快。

图 7 刚度退化曲线Fig.7 Rigidity retrogradation curves

2.5 耗能能力

各试件达到屈服荷载、峰值荷载及破坏荷载时的累积耗能见表5。

表 5 试件的累积耗能Table 5 Cumulated energy depletion of specimens

由表5分析可得：

1) 对于无构造柱试件，HDC加固试件破坏时的总耗能均有大幅提高，其中试件AW-1、AW-2与AW-3的总耗能分别是未加固试件AW-0的4.1倍、1.4倍(条带剥落)和3.4倍。

2) 相比试件AW-0，由于构造柱的约束作用，试件AWG-0的总耗能提高了48%。相比试件AWG-0，试件AWG-1的总耗能提高了40%；停止加载时，试件AWG-1的残余承载力较高，墙面损伤较小，说明其耗能能力尚未得到充分发挥。

3 承载力分析

本文所述的6个试件在试验中分别产生了三种破坏形态：对角剪切破坏、剪切-滑移破坏和弯剪破坏。根据各试件的加固形式及其破坏形态，可按下述方法计算其水平承载力。

3.1 未加固试件受剪承载力

1) 未加固试件AW-0发生对角剪切破坏，可根据主拉应力强度理论，按我国规范[25]中给出的承载力计算公式计算墙体的受剪承载力：

式中：σ0为AAC砌体墙的竖向压应力；Am为AAC砌体墙的横截面面积；fv0,m为AAC砌体墙抗剪强度的平均值，可参考《砌体结构设计规范》[26]按下式计算：

式中：f2为砂浆的抗压强度平均值；k5为系数，本文取0.09。

2) 对于试件AWG-0，考虑墙体两侧构造柱的约束作用，按下式计算其受剪承载力[16]：

式中：ηc为构造柱约束增强系数，可按我国规范[27]相关规定取值，本文砂浆抗压强度平均值3.1 MPa，取ηc=1.25。

3.2 HDC加固墙体水平承载力

1) HDC单面加固试件AW-1发生剪切滑移破坏；因此，以底部截面为控制截面，根据剪摩强度理论计算该试件的受剪承载力。

试件底部截面受力状态如图8所示。忽略开裂区域墙体的抗剪强度，将受压区作为墙体的有效抗剪截面；根据平衡条件，试件AW-1的水平承载力计算如下[17−18]。

由平截面假定及力的平衡条件可得：

对截面中点取矩可得：

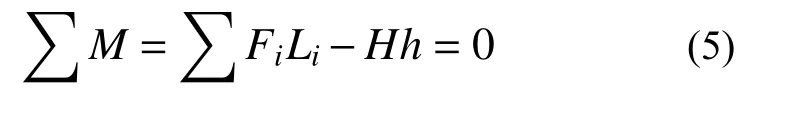
式中：Em为AAC砌体墙的弹性模量；EH为HDC的弹性模量；xc为截面未开裂区域长度，为简化计算，取为墙体长度的一半，xc=1215 mm；FN1为截面受压区AAC砌体墙合力；FN2为受压区HDC面层合力；FT1、FT2分别为截面受拉区HDC面层未开裂段合力和开裂段合力[18]；Li为上述各合力作用点到截面中点所对应的距离。

图 8 截面受力状态示意图Fig.8 Schematic diagram of stress state of cross section

H为墙体底部有效受剪截面内的剪力，可用下式计算：

式中：φ为砂浆内摩擦角[18]；vcr为HDC截面剪切强度[28]；fcH为HDC轴心抗压强度，由立方体平均抗压强度换算得到[22]。

2) 为便于设计计算，本文采用叠加法计算试件AWG-1的水平承载力：

式中：Vm为加固试件中原砌体墙的水平承载力，按式(3)计算，VH为HDC面层的受剪承载力，根据本课题组以往研究成果，按下式计算[29]：

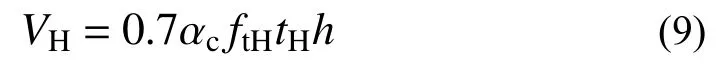
式中：αc为HDC强度利用系数，取0.7；ftH为HDC抗拉强度；tH为HDC面层厚度；h为墙体水平方向长度。

3) 在荷载作用下HDC条带与弱框架的作用类似。因此，引入等效受压斜撑模型计算试件AW-2及AW-3的受剪承载力。如图9所示，将原砌体墙等效为一个沿墙体对角线方向、具有特定宽度及力学性能的斜撑，将HDC条带等效为墙体两侧的构造柱，并采用叠加法来计算HDC条带加固墙体的受剪承载力[30−31]：

图 9 约束砖砌体墙的等效受压斜撑模型Fig.9 Equivalent compressive diagonal bracing model for constrained-brick masonry walls

为原砌体墙的受剪承载力，按下式计算：

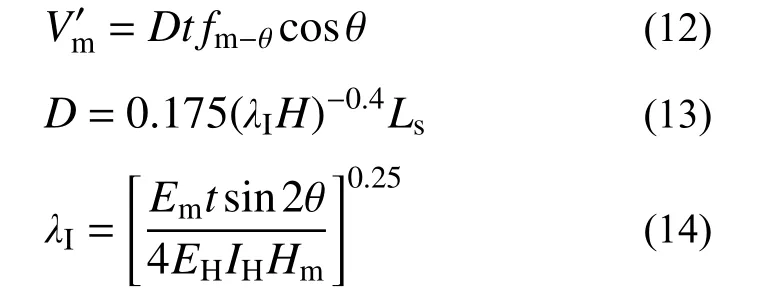
式中：t为墙体厚度；fm-θ为砌体沿斜撑方向的抗压强度，本文近似取fm-θ=0.85fm[31]；D为斜撑宽度；H为圈梁中线之间的构造柱高度；Ls为受压斜撑的长度；λI为计算受压斜撑宽度的参数；Em为墙体材料的弹性模量；EH为HDC条带部分等效弹性模量；IH为HDC条带部分等效惯性矩；Hm为墙体高度；θ为受压斜撑与水平方向的夹角；fm为AAC砌体的抗压强度平均值，可参考我国规范[26]按下式计算：

式中：α为与块体高度及砌体类别有关的参数，本文取0.5；k1为与块体类别有关的参数，本文取0.78；f1为AAC砌块抗压强度平均值；k2为修正系数，本文取1.0。

3.3 计算结果验证

本次试验各试件的水平承载力计算结果与试验结果如表6所示。

表 6 计算结果与试验结果比较Table 6 Comparison of maximum loads

由表6可知，本文采用的HDC加固蒸压加气混凝土砌块砌体墙的水平承载力计算方法，其计算值与试验值基本吻合，可为此类构件的加固设计提供参考。但是，本次试验的试件数量较少，后期将开展进一步的试验及理论分析。

4 结论

通过2片未加固AAC墙体和4片采用HDC加固的AAC墙体的试验研究结果，可初步得到以下结论：

(1) HDC面层及配筋条带加固可对AAC墙体形成有效约束，从而提高无筋AAC砌体墙的延性及耗能能力。加固后墙体的水平承载力及耗能能力均高于构造柱约束墙体，且变形能力与之相近，这两种方式可作为提高AAC墙体抗震性能的有效加固措施。

(2) 单面HDC面层加固构造柱约束AAC墙体破坏时，墙体损伤较小，残余承载力较高，有利于结构的震后修复及在余震中继续承受荷载。

(3) 双面HDC条带加固的试件出现了HDC条带剥落，未能充分发挥HDC条带的加固效果，但双面配筋条带加固的试件未出现剥落。因此，通过锚固措施防止HDC条带剥落，可以充分发挥HDC条带的加固效果。

(4) 基于试验中AAC砌体墙的破坏模式，提出了各加固方式下AAC砌体墙的水平承载力计算方法，可为HDC加固AAC墙体受剪承载力计算提供参考。